User:Tohline/H BookTiledMenu

Tiled Menu

Context

Global Energy Considerations

Principal Governing Equations (PGEs)		Continuity		Euler		1st Law of Thermodynamics		Poisson

 

Equation of State (EOS)		Ideal Gas		Total Pressure

Spherically Symmetric Configurations

(Initially) Spherically Symmetric Configurations

 

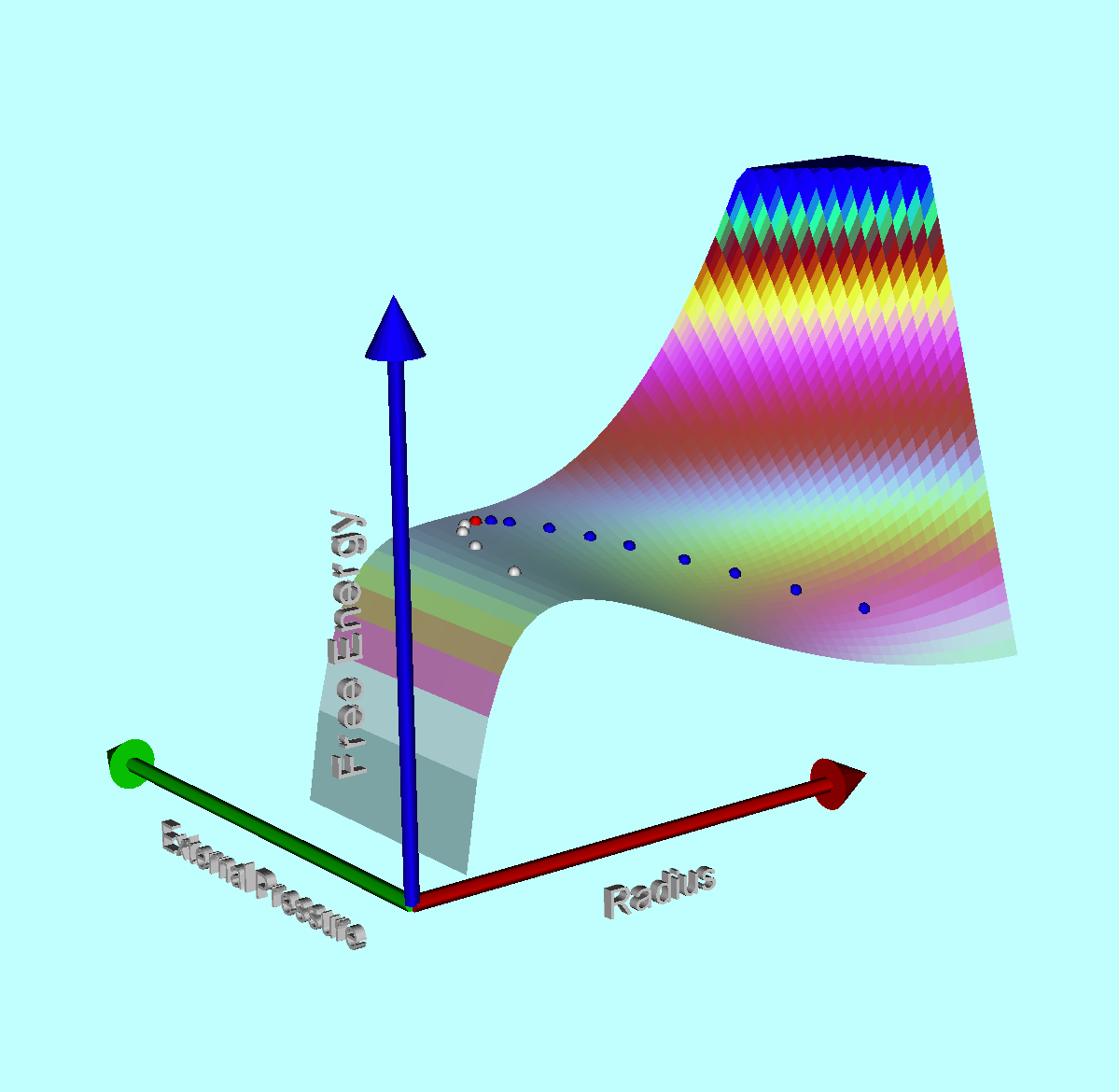
		Structural Form Factors		Free-Energy of Spherical Systems

One-Dimensional PGEs

Equilibrium Structures

1D STRUCTURE

 

		Scalar Virial Theorem

Hydrostatic Balance Equation		<math>~\frac{dP}{dr} = - \frac{GM_r \rho}{r^2}</math>		Solution Strategies

 

Isothermal Sphere		<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>		via Direct Numerical Integration

 

Isolated Polytropes		Lane (1870)		<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>		Known Analytic Solutions		via Direct Numerical Integration		via Self-Consistent Field (SCF) Technique

 

Zero-Temperature White Dwarf		Chandrasekhar Limiting Mass (1935)

 

Virial Equilibrium of Pressure-Truncated Polytropes

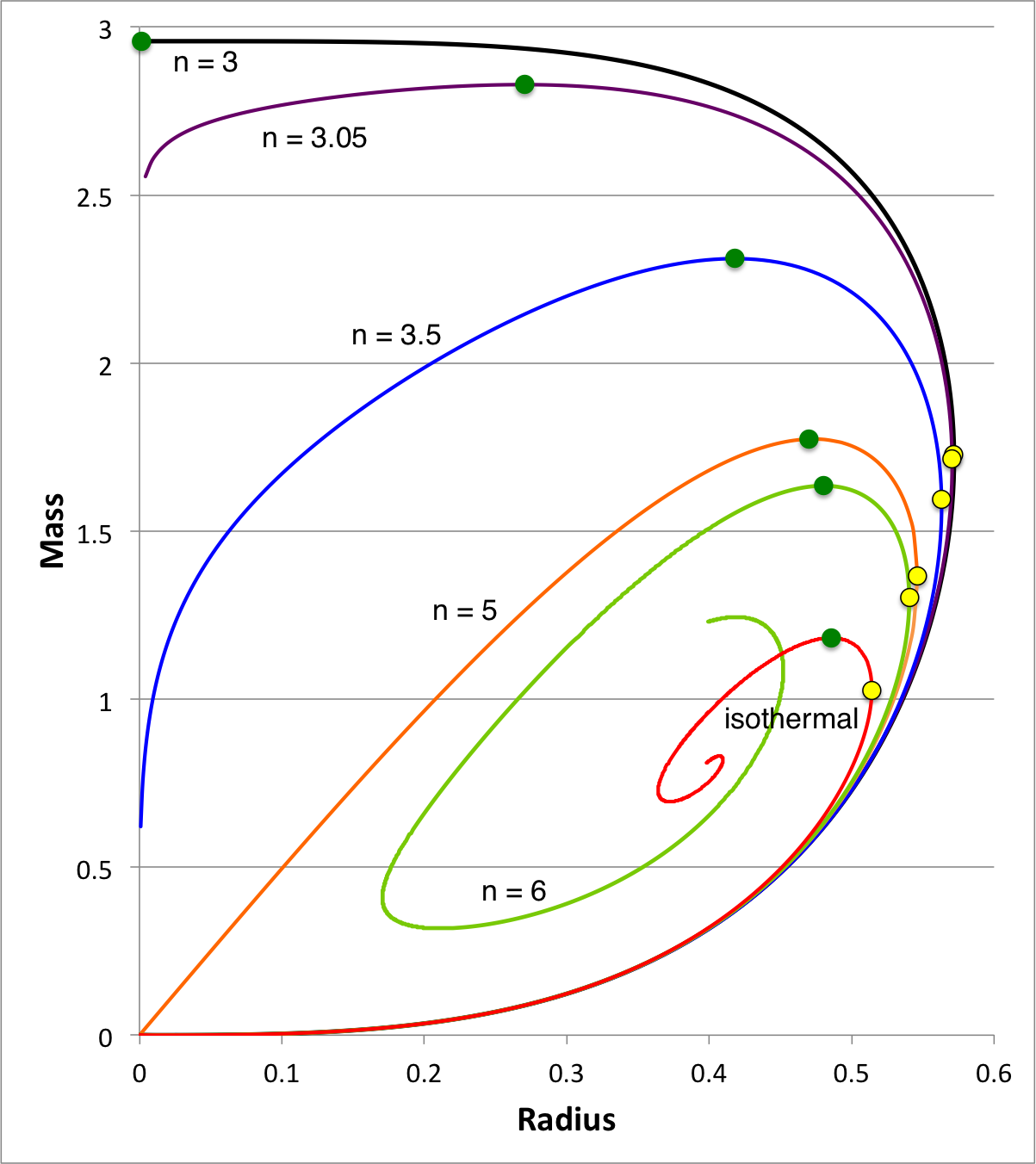
Pressure-Truncated Configurations		Bonnor-Ebert (Isothermal) Spheres (1955 - 56)		Polytropes		Equilibrium Sequence Turning-Points ♥				Turning-Points (Broader Context)

 

Free Energy of Bipolytropes (nc, ne) = (5, 1)

Composite Polytropes (Bipolytropes)		Schönberg- Chandrasekhar Mass (1942)		Analytic (nc, ne) = (5, 1)		Analytic (nc, ne) = (1, 5)

 

Stability Analysis

1D STABILITY

 

		Variational Principle

Radial Pulsation Equation		Example Derivations & Statement of Eigenvalue Problem		(poor attempt at) Reconciliation		Relationship to Sound Waves

 

Jeans (1928) or Bonnor (1957)		Ledoux & Walraven (1958)		Rosseland (1969)

 

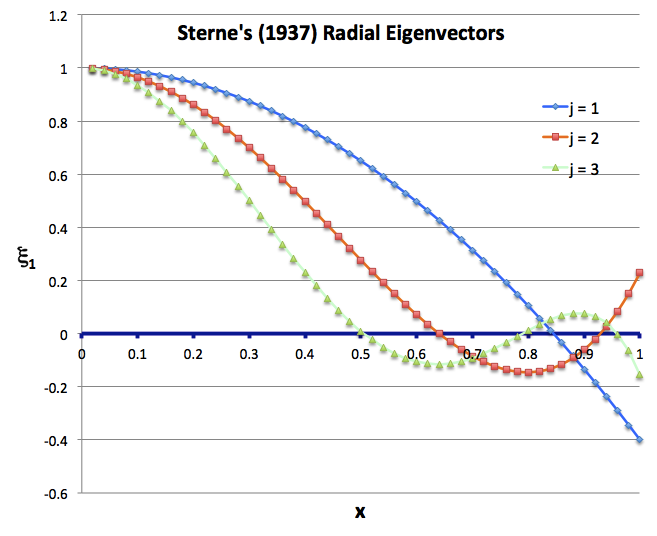
Uniform-Density Configurations		Sterne's Analytic Sol'n of Eigenvalue Problem (1937)

 

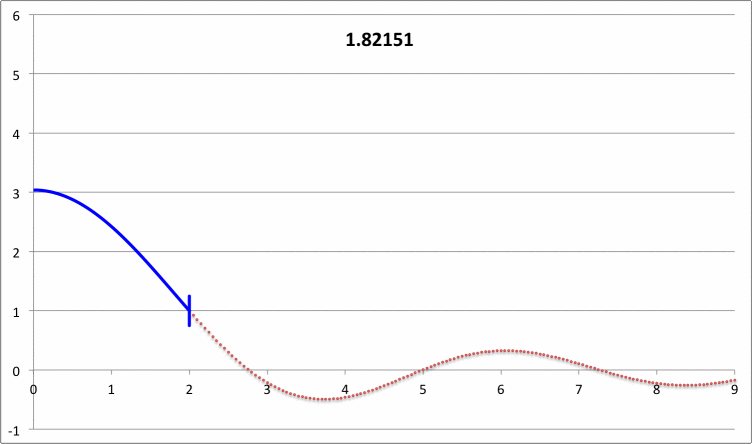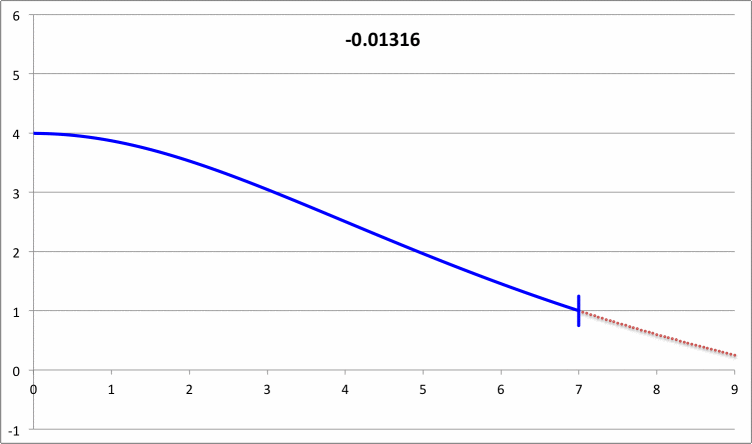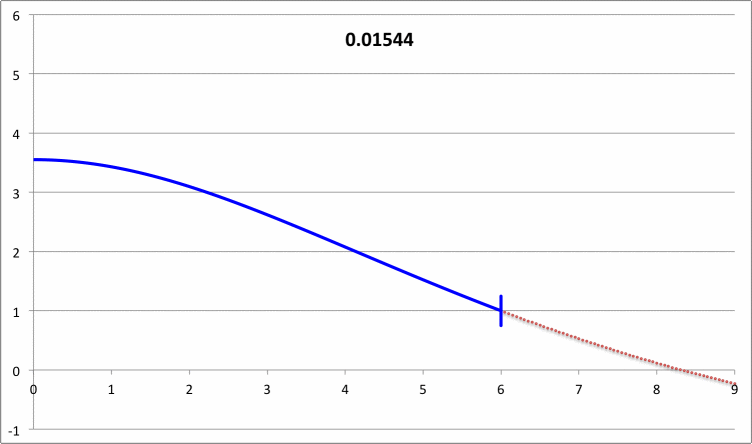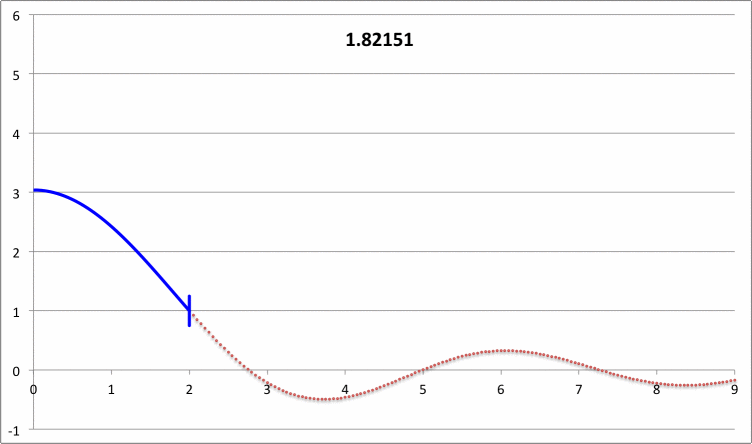
Pressure-Truncated Isothermal Spheres		<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math> where:    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>		via Direct Numerical Integration

Yabushita's Analytic Sol'n for Marginally Unstable Configurations (1974)		<math>~\sigma_c^2 = 0 \, , ~~~~\gamma_\mathrm{g} = 1</math>  and   <math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} </math>

 

Polytropes		<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math> where:    <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math>    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>		Isolated n = 3 Polytrope				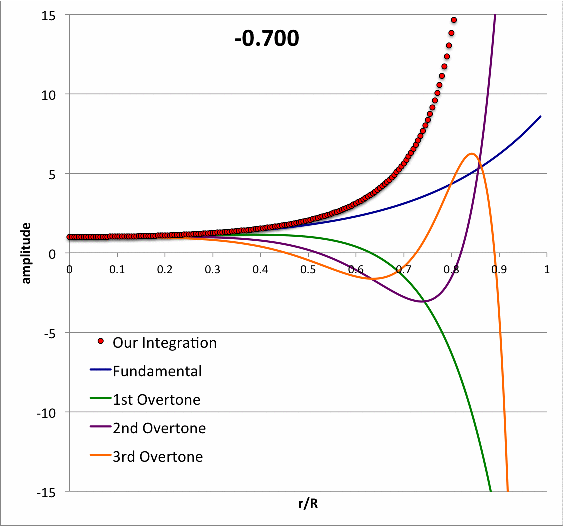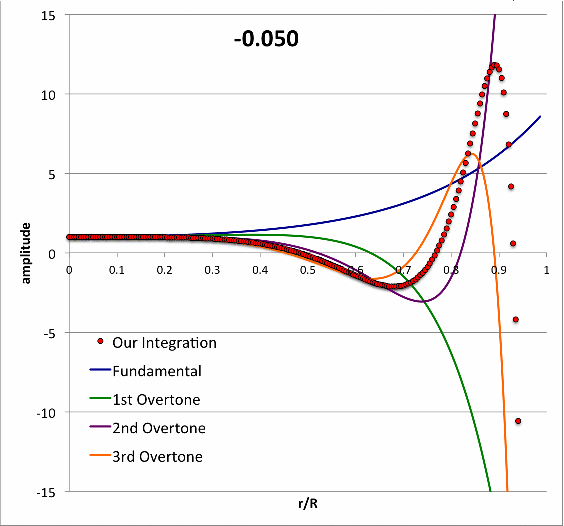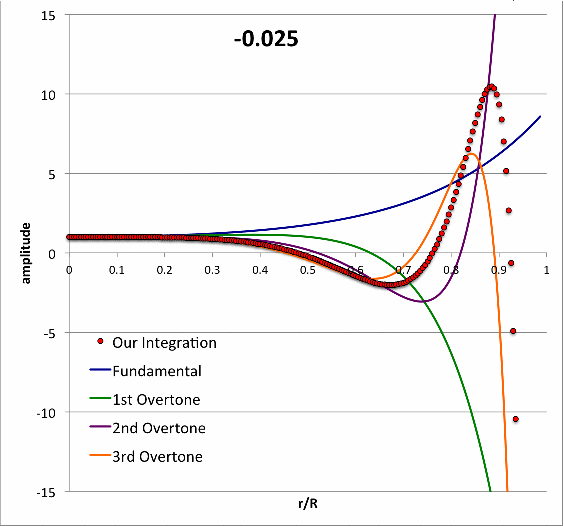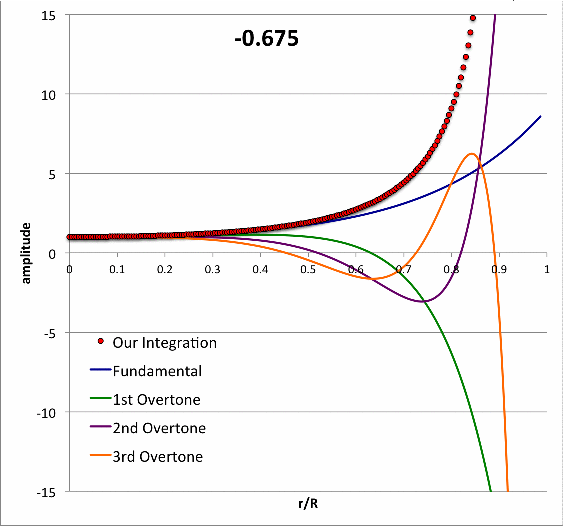Pressure-Truncated n = 5 Configurations

Exact Demonstration of B-KB74 Conjecture		Exact Demonstration of Variational Principle		Pressure-Truncated n = 5 Polytropes

Our Analytic Sol'n for Marginally Unstable Configurations (2017) ♥		<math>~\sigma_c^2 = 0 \, , ~~~~\gamma_\mathrm{g} = (n+1)/n</math>  and   <math>~x = \frac{3(n-1)}{2n}\biggl[1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\xi \theta^{n}}\biggr) \frac{d\theta}{d\xi}\biggr] </math>

 

BiPolytropes		Murphy & Fiedler (1985b) (nc, ne) = (1,5)		Our Broader Analysis

 

Nonlinear Dynamical Evolution

1D DYNAMICS

 

Free-Fall Collapse

 

Collapse of Isothermal Spheres		via Direct Numerical Integration		Similarity Solution

 

Collapse of an Isolated n = 3 Polytrope

 

Two-Dimensional Configurations (Axisymmetric)

(Initially) Axisymmetric Configurations

 

"As a practical matter, discussions of the effect of rotation on self-gravitating fluid masses divide into two categories: the structure of steady-state configurations, and the oscillations and the stability of these configurations."

— Drawn from N. R. Lebovitz (1967), ARAA, 5, 465

We add a third category, namely, the nonlinear dynamical evolution of systems that are revealed via stability analyses to be unstable.

PGEs for Axisymmetric Systems

Axisymmetric Equilibrium Structures

2D STRUCTURE

 

Constructing Axisymmetric Equilibrium Configurations		Axisymmetric Instabilities to Avoid		Simple Rotation Profiles		Hachisu Self-Consistent-Field [HSCF] Technique		Solving the Poisson Equation

 

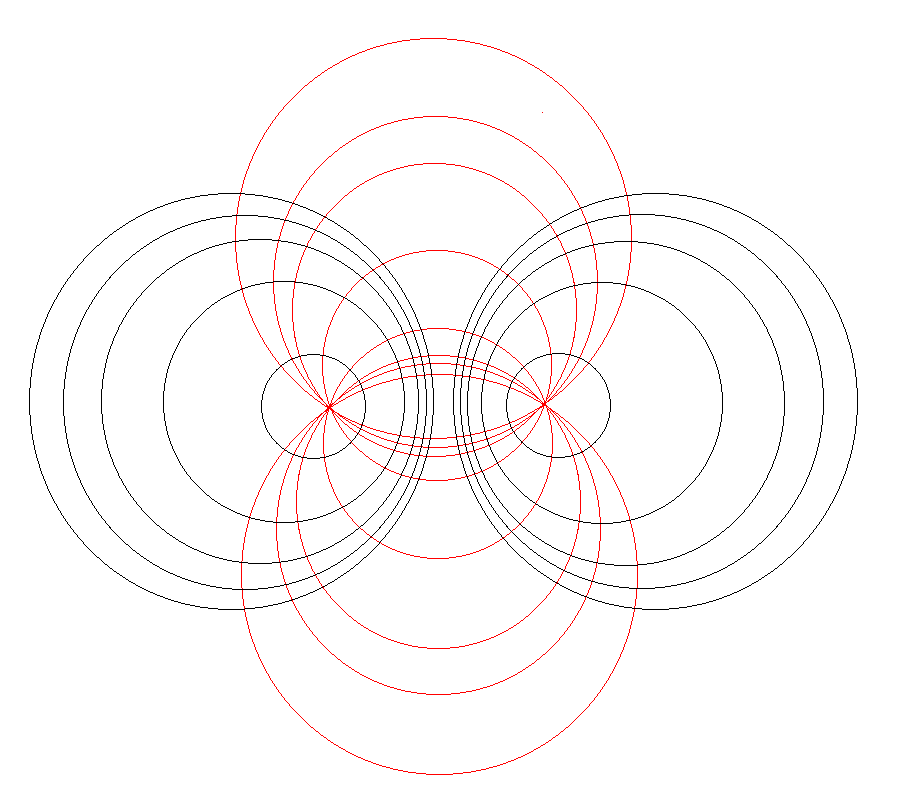
Using Toroidal Coordinates to Determine the Gravitational Potential				Attempt at Simplification ♥		Wong's Analytic Potential (1973)

Spheroidal & Spheroidal-Like

Uniform-Density (Maclaurin) Spheroids		Maclaurin's Original Text & Analysis (1742)

 

Rotationally Flattened Isothermal Configurations		Hayashi, Narita & Miyama's Analytic Sol'n (1982)		Review of Stahler's (1983) Technique

 

Rotationally Flattened Polytropes		Example Equilibria

 

Rotationally Flattened White Dwarfs		Ostriker Bodenheimer & Lynden-Bell (1966)		Example Equilibria

Toroidal & Toroidal-Like

Definition: anchor ring

Massless Polytropic Configurations		Papaloizou-Pringle Tori (1984)

 

Self-Gravitating Incompressible Configurations		Dyson (1893)		Dyson-Wong Tori

 

Self-Gravitating Compressible Configurations		Ostriker (1964)

 

Stability Analysis

2D STABILITY

 

Sheroidal & Spheroidal-Like

Linear Analysis of Bar-Mode Instability		Bifurcation from Maclaurin Sequence		Traditional Analyses		Time-Dependent Simulations

 

• T. G. Cowling & R. A. Newing (1949), ApJ, 109, 149: The Oscillations of a Rotating Star
• M. J. Clement (1965), ApJ, 141, 210: The Radial and Non-Radial Oscillations of Slowly Rotating Gaseous Masses
• P. H. Roberts & K. Stewartson (1963), ApJ, 137, 777: On the Stability of a Maclaurin spheroid of small viscosity
• C. E. Rosenkilde (1967), ApJ, 148, 825: The tensor virial-theorem including viscous stress and the oscillations of a Maclaurin spheroid
• S. Chandrasekhar & N. R. Lebovitz (1968), ApJ, 152, 267: The Pulsations and the Dynamical Stability of Gaseous Masses in Uniform Rotation
• C. Hunter (1977), ApJ, 213, 497: On Secular Stability, Secular Instability, and Points of Bifurcation of Rotating Gaseous Masses
• J. N. Imamura, J. L. Friedman & R. H. Durisen (1985), ApJ, 294, 474: Secular stability limits for rotating polytropic stars
• J. R. Ipser & L. Lindblom (1990), ApJ, 355, 226: The Oscillations of Rapidly Rotating Newtonian Stellar Models
• J. R. Ipser & L. Lindblom (1991), ApJ, 373, 213: The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects
• J. N. Imamura, J. L. Friedman & R. H. Durisen (2000), ApJ, 528, 946: Nonaxisymmetric Dynamic Instabilities of Rotating Polytropes. II. Torques, Bars, and Mode Saturation with Applications to Protostars and Fizzlers
• G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche ellipsoids

 

Toroidal & Toroidal-Like

Defining the Eigenvalue Problem

 

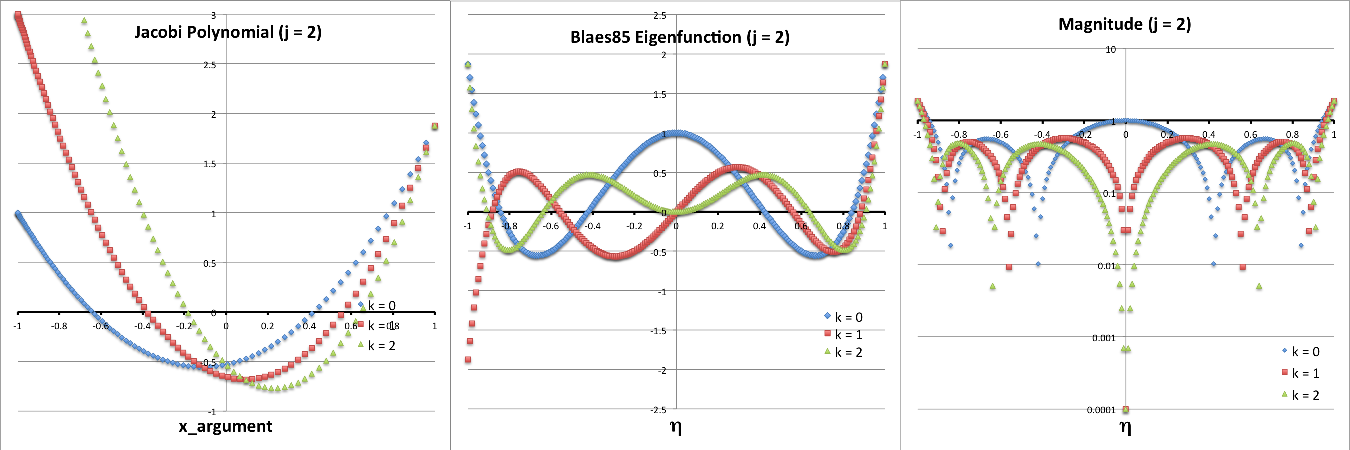
(Massless) Papaloizou-Pringle Tori		Analytic Analysis by Blaes (1985)

 

Nonlinear Dynamical Evolution

2D DYNAMICS

 

Free-Fall Collapse of an Homogeneous Spheroid

 

Two-Dimensional Configurations (Nonaxisymmetric Disks)

Infinitesimally Thin, Nonaxisymmetric Disks

 

2D STRUCTURE

 

Constructing Infinitesimally Thin Nonaxisymmetric Disks

 

Three-Dimensional Configurations

(Initially) Three-Dimensional Configurations

 

Equilibrium Structures

3D STRUCTURE

 

Special numerical techniques must be developed "to build three-dimensional compressible equilibrium models with complicated flows." To date … "techniques have only been developed to build compressible equilibrium models of nonaxisymmetric configurations for a few systems with simplified rotational profiles, e.g., rigidly rotating systems (Hachisu & Eriguchi 1984; Hachisu 1986), irrotational systems (Uryū & Eriguchi 1998), and configurations that are stationary in the inertial frame (Uryū & Eriguchi 1996)."

— Drawn from §1 of Ou (2006), ApJ, 639, 549

Ellipsoidal & Ellipsoidal-Like

Constructing Ellipsoidal & Ellipsoidal-Like Configurations

 

Jacobi Ellipsoids

 

• B. P. Kondrat'ev (1985), Astrophysics, 23, 654: Irrotational and zero angular momentum ellipsoids in the Dirichlet problem
• D. Lai, F. A. Rasio & S. L. Shapiro (1993), ApJS, 88, 205: Ellipsoidal Figures of Equilibrium: Compressible models

Binary Systems

• S. Chandrasekhar (1933), MNRAS, 93, 539: The equilibrium of distorted polytropes. IV. the rotational and the tidal distortions as functions of the density distribution
• S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids

Roche's problem is concerned with the equilibrium and the stability of rotating homogeneous masses which are, further, distorted by the constant tidal action of an attendant rigid spherical mass.

 

Stability Analysis

3D STABILITY

 

Binary Systems

• S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids
• G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche Ellipsoids

Nonlinear Evolution

3D DYNAMICS

 

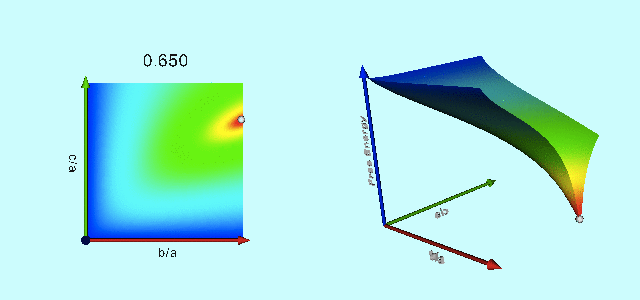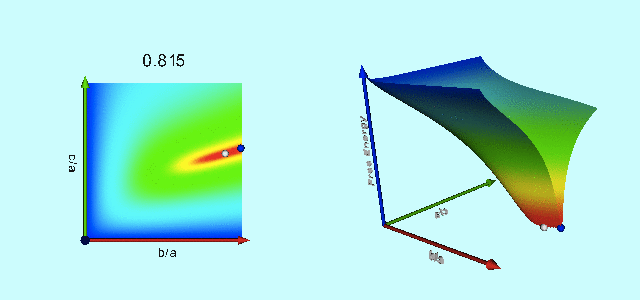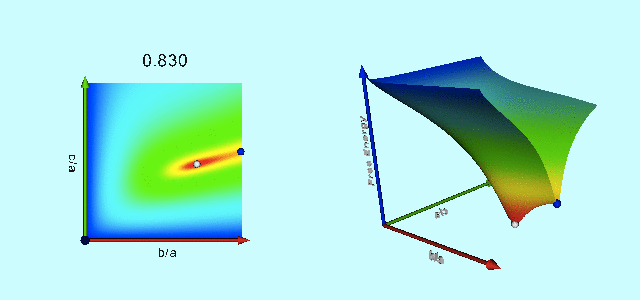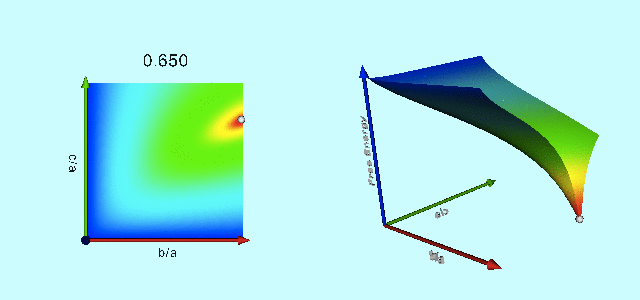
		Free-Energy Evolution from the Maclaurin to the Jacobi Sequence

Fission Hypothesis

 

Secular

• M. Fujimoto (1971), ApJ, 170, 143: Nonlinear Motions of Rotating Gaseous Ellipsoids
• W. H. Press & S. A. Teukolsky (1973), ApJ, 181, 513: On the Evolution of the Secularly Unstable, Viscous Maclaurin Spheroids
• S. L. Detweiler & L. Lindblom (1977), ApJ, 213, 193: On the evolution of the homogeneous ellipsoidal figures.

See Also

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation