User:Tohline/2DStructure/ToroidalCoordinateIntegrationLimits
Toroidal-Coordinate Integration Limits
In support of our accompanying discussion of the gravitational potential of a uniform-density circular torus, here we explain in detail what limits of integration must be specified in order to accurately determine the volume — and, hence also the total mass — of such a torus using toroidal coordinates.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Mapping from Cylindrical to Toroidal Coordinates
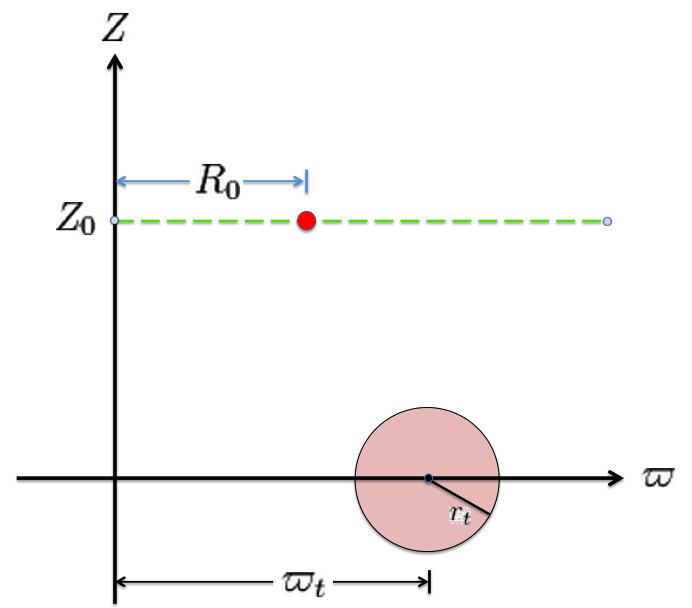
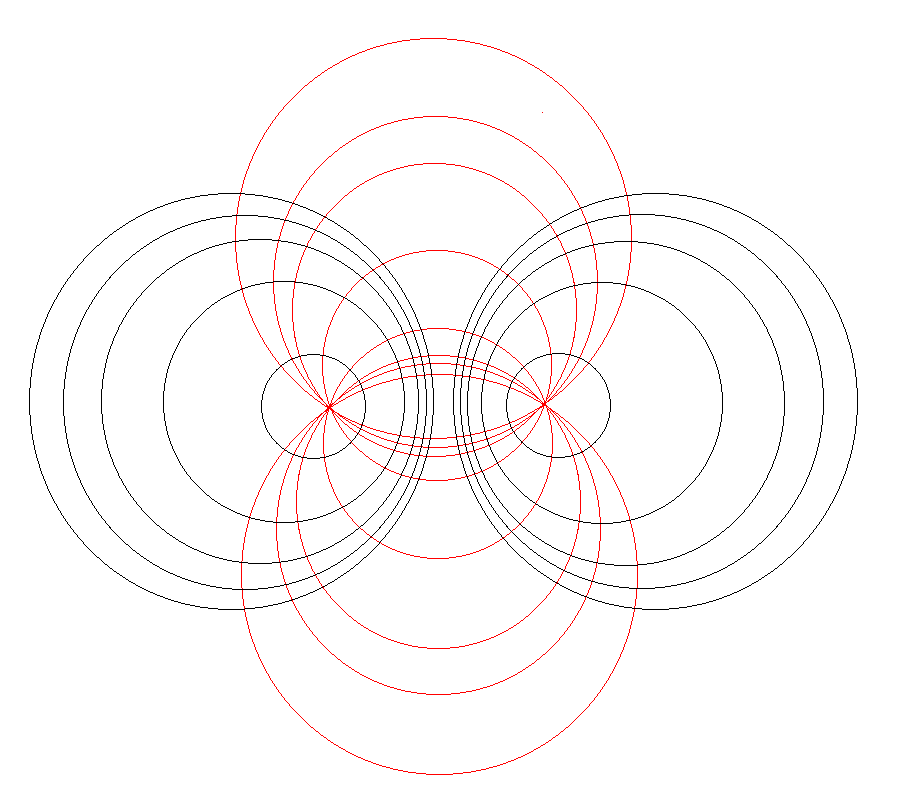
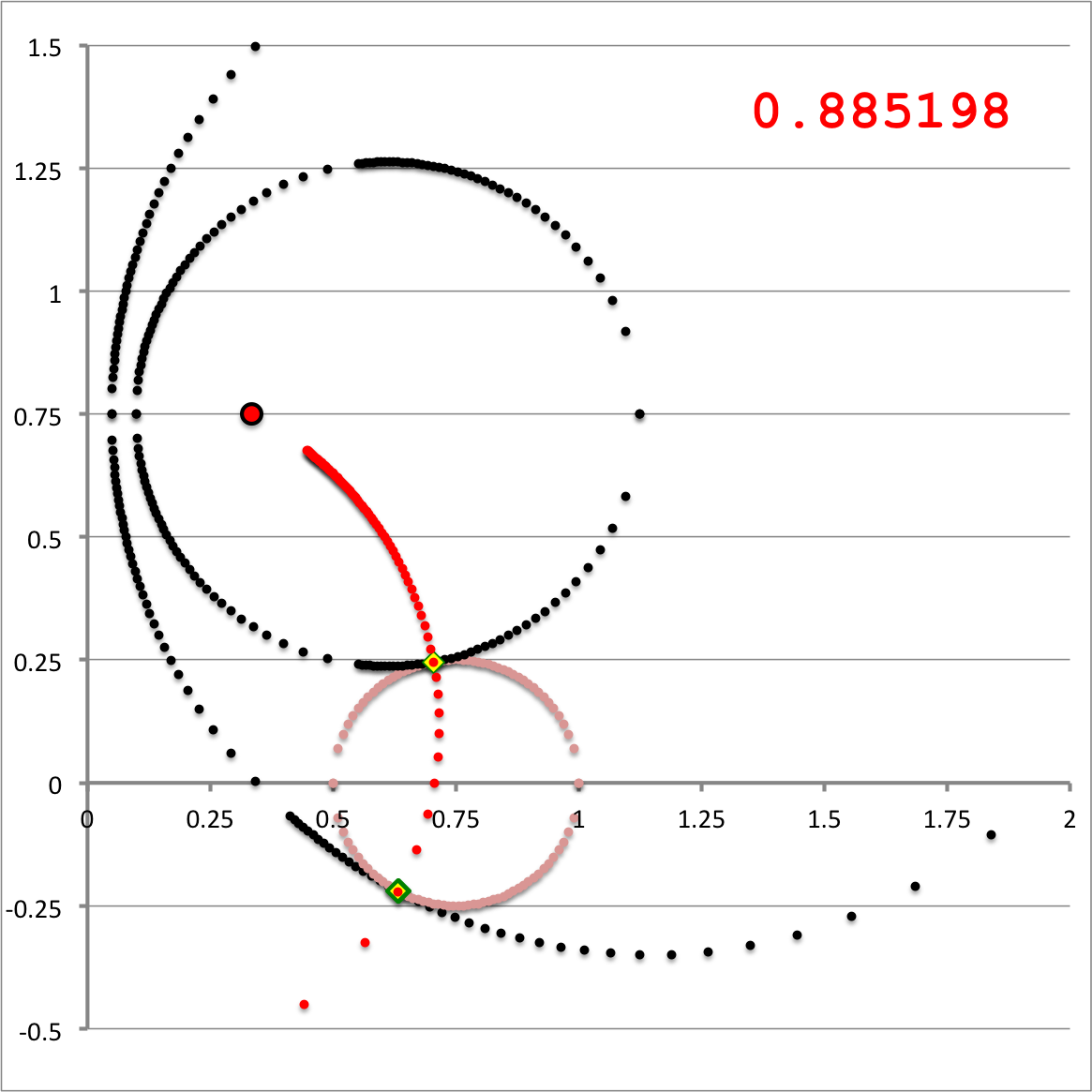
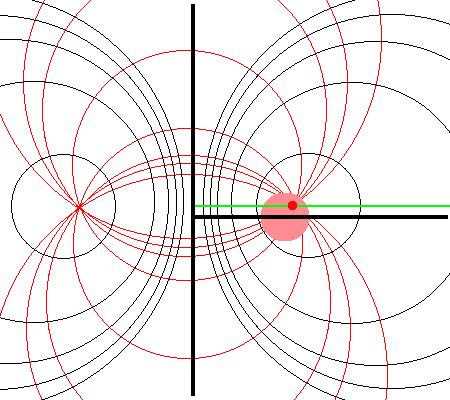
Referencing the illustration displayed in the left-hand panel of Figure 1, our goal is to determine the gravitational potential at any cylindrical-coordinate location <math>~(R_0, Z_0)</math> due to a uniform-density circular torus whose major radius is <math>~\varpi_t</math> and whose minor, cross-sectional radius is <math>~r_t</math>. Here we explain how a toroidal coordinate system <math>~(\xi_1, \xi_2)</math> — as defined, for example, by MF53 and as illustrated schematically in the right-hand panel of Figure 1 — can be used to reduce the geometric complexity of this problem. Note that, in our illustration, each black circle identifies a <math>\xi_1 = </math> constant surface and each red circle identifies a <math>\xi_2 = </math> constant surface. Note, as well, that the overall length scale (not labeled in our schematic diagram) is set by the distance, <math>~a</math>, from the vertical symmetry axis to the origin of the toroidal coordinate system — the point (actually, the axisymmetric ring) at which all the red circles intersect one another. Here we will show how, when using an appropriately aligned toroidal coordinate system, the three-dimensional, weighted integral over the mass distribution that is required to determine the gravitational potential at any location can be reduced to the sum of a small number (1 - 4) of one-dimensional integrals over the "radial" coordinate, <math>~\xi_1</math>.
| Figure 1: Meridional slice through … | |
|---|---|
| (Pink) Circular Torus | Toroidal Coordinate System (schematic) (see also Wikipedia's Apollonian Circles) |
|
The pink circle represents the meridional cross-section through an axisymmetric, circular torus that lies in the equatorial plane of a cylindrical <math>~(\varpi, Z)</math>, coordinate system. The torus has a major axis of length, <math>~\varpi_t</math>, and a minor, cross-sectional radius of length, <math>~r_t</math>. The red circular dot identifies the cylindrical-coordinate location, <math>~(R_0, Z_0)</math>, at which the gravitational potential is to be evaluated. |
As is explained more fully in Wikipedia's discussion of toroidal coordinates, rotating this two-dimensional bipolar coordinate system about the vertical axis produces a three-dimensional toroidal coordinate system. Black circles centered on the horizontal axis become circular tori — each identifying an axisymmetric, <math>\xi_1 =</math> constant surface; whereas, red circles centered on the vertical axis become spheres — each identifying an axisymmetric, <math>\xi_2 =</math> constant surface. |
Special Case Alignment
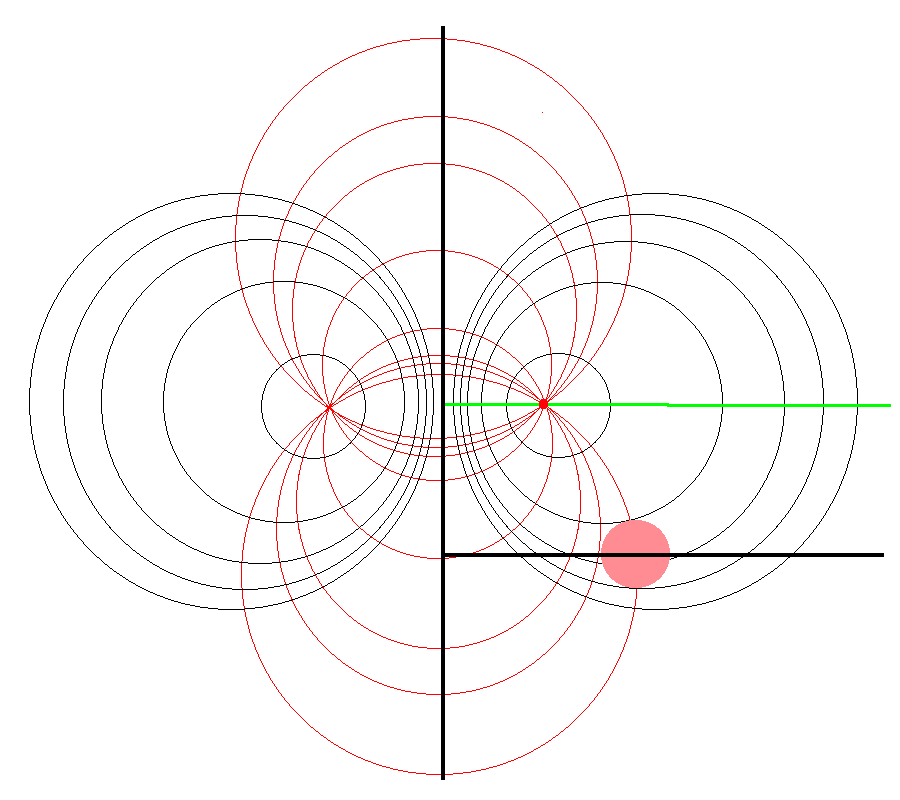
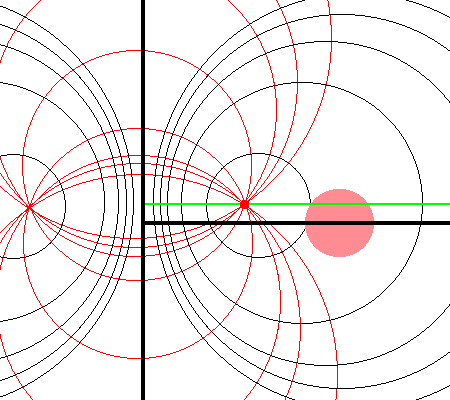
It should perhaps not be surprising to find that a toroidal coordinate system can be effectively used to quantitatively describe some properties — certainly the volume and possibly the gravitational potential — of circular tori because each <math>\xi_1 = </math> constant surface in a toroidal coordinate system (see the black circles in the right-hand panel of Figure 1) defines the surface of an axisymmetric, circular torus. In order to map from a cylindrical-coordinate representation of a circular torus (see the left-hand panel of Figure 1) to a toroidal-coordinate representation of that torus, at first glance it would seem reasonable to establish the alignment depicted schematically in Figure 2. That is, align the horizontal and vertical axes of the bipolar coordinate system (right-hand panel of Figure 1) with, respectively, the <math>\varpi-</math>axis and the <math>Z-</math>axis of the cylindrical coordinate system, then scale the overall size of the bipolar coordinate system until one <math>\xi_1 = </math> constant surface perfectly aligns with the surface of the (pink) torus.
| Figure 2: Schematic Illustration of "Special Case" Alignment |
|---|
|
Here, a mapping from cylindrical coordinates to toroidal coordinates is achieved by aligning the horizontal and vertical axes of the bipolar coordinate system (right-hand panel of Figure 1) with, respectively, the <math>\varpi-</math>axis and the <math>Z-</math>axis of the cylindrical coordinate system, then scaling the overall size of the bipolar coordinate system, <math>~a</math>, until one <math>\xi_1 = </math> constant surface perfectly aligns with the surface of the (pink) torus. |
This is the "special case" alignment that we have discussed in an accompanying chapter. It is achieved by setting the scale-length, <math>~a</math>, of the toroidal-coordinate system to a value given by the expression,
|
<math>~a</math> |
<math>~=</math> |
<math>~\sqrt{\varpi_t^2 - r_t^2}\, ,</math> |
which means that the "radial" toroidal coordinate that aligns with the surface of the (pink) torus has the value,
|
<math>~\xi_1</math> |
<math>~=</math> |
<math>~\frac{\varpi_t}{r_t} \, .</math> |
While the special alignment depicted in Figure 2 might at first glance seem reasonable, we have found that it does not generally enable us to transform the multi-dimensional integral expression for the gravitational potential into a one-dimensional integral over <math>~\xi_1</math>, as desired.
Practical Transformation
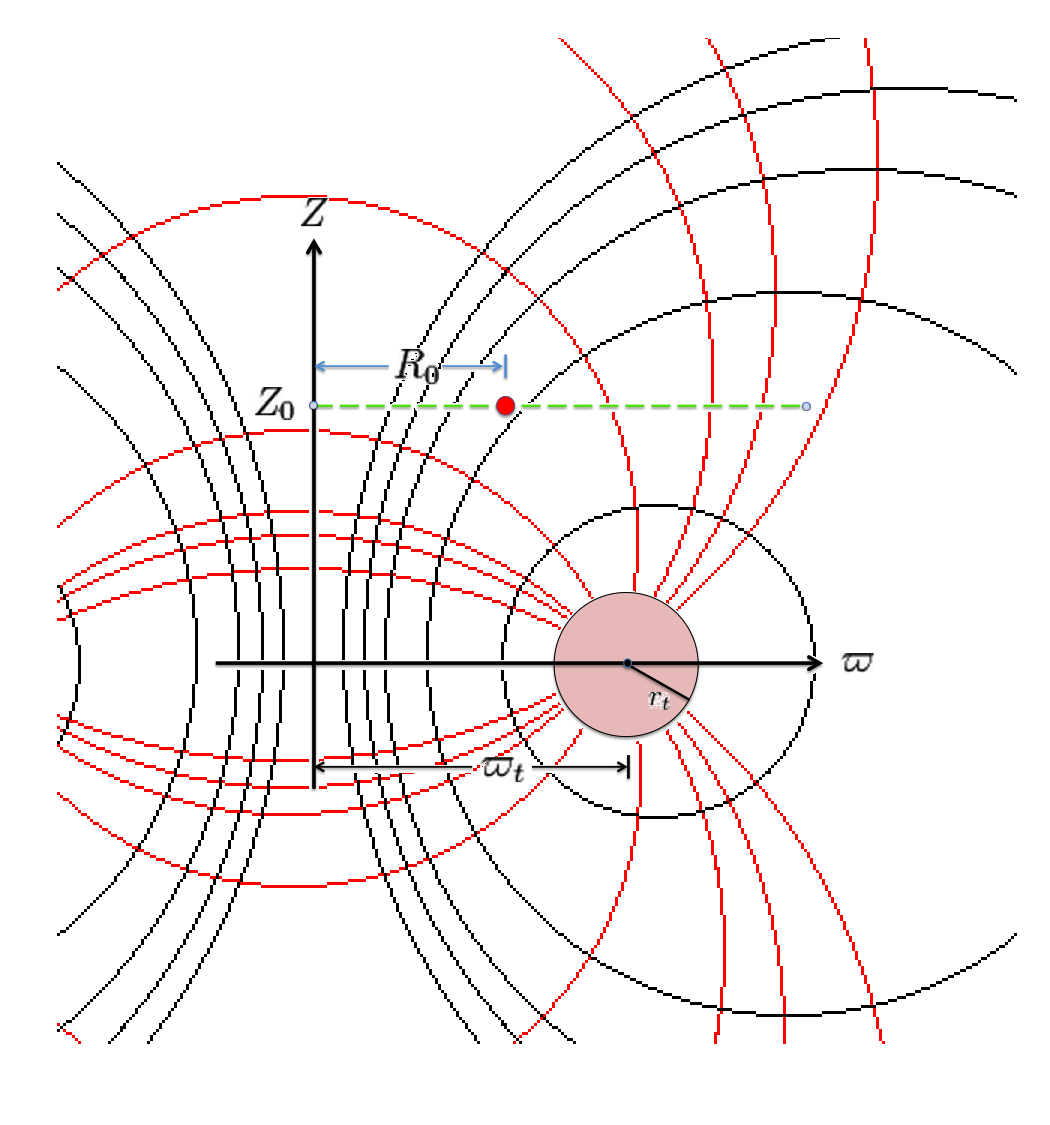
However, we have discovered that this desired transformation can be accomplished by shifting the toroidal-coordinate system vertically and scaling it such that its off-axis "origin" aligns with the cylindrical-coordinate location, <math>~(R_0, Z_0)</math>, at which the gravitational potential is to be evaluated. The left-hand panel of Figure 3 illustrates what results from aligning in this manner the left-hand and right-hand panels of Figure 1. The origin of the toroidal coordinate system sits on the green line-segment, a distance <math>~Z = Z_0</math> above the equatorial plane of the torus, and a distance <math>~a = R_0</math> from the symmetry axis.
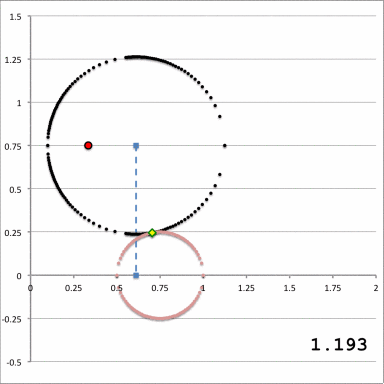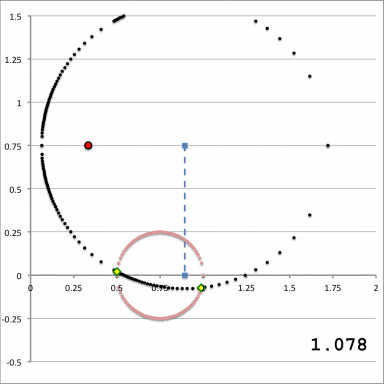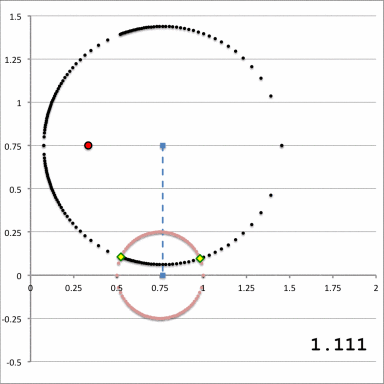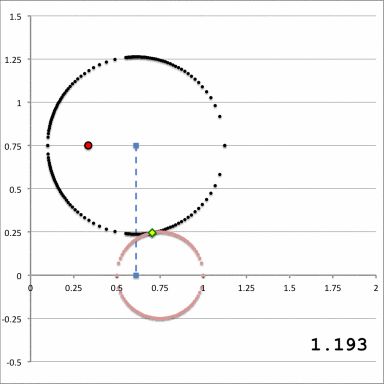
| Figure 3: Quantitative Illustration of Employed Toroidal Coordinate System | ||
|---|---|---|
The middle and right-hand panels of Figure 3 display quantitatively how the boundary of the (pink) circular torus is defined in toroidal coordinates when an alignment of coordinate systems is made, as illustrated in the left-hand panel of Figure 3, for the parameter values: <math>~(R_0, Z_0) = (\tfrac{1}{3}, \tfrac{3}{4})</math> and <math>~(\varpi_t, r_t) = (\tfrac{3}{4}, \tfrac{1}{4})</math>. As the middle panel shows, black toroidal-coordinate circles intersect and/or thread through the (pink) torus for values of the radial coordinate in the range, <math>1.045 \leq \xi_1 \leq 1.193</math>. And, as the right-hand panel shows, the red toroidal-coordinate circle that corresponds to the angular-coordinate value, <math>~\xi_2 = 0.885198</math>, not only threads through the (pink) torus but identifies the "angle" at which the two limiting <math>\xi_1 =</math> constant circles touch the surface of the torus. The derivations that have led to the construction of these two figure panels are presented in an accompanying discussion.
One-Dimensional Integral Equations
Volume of Circular Torus
|
Note that when either integration limit, <math>~\gamma_i</math> or <math>~\Gamma_i</math>, is plus one, the integrand inside the curly braces becomes,
|
<math>~\biggl\{~~\biggr\}_{\xi_2 = +1}</math> |
<math>~~\rightarrow~~</math> |
<math>~ \biggl\{0 + \biggl[ \frac{(2\xi_1^2 + 1)}{(\xi_1^2-1)^{5/2}}\biggr] \cos^{-1}\biggl[ 1 \biggr] \biggr\} = 0 \, . </math> |
Alternatively, when either integration limit, <math>~\gamma_i</math> or <math>~\Gamma_i</math>, is minus one, the integrand inside the curly braces becomes,
|
<math>~\biggl\{~~\biggr\}^{\xi_2 = -1}</math> |
<math>~~\rightarrow~~</math> |
<math>~ \biggl\{0 + \biggl[ \frac{(2\xi_1^2 + 1)}{(\xi_1^2-1)^{5/2}}\biggr] \cos^{-1}\biggl[- 1 \biggr] \biggr\} = \pi \biggl[ \frac{(2\xi_1^2 + 1)}{(\xi_1^2-1)^{5/2}}\biggr] \, . </math> |
(In principle, the arccosine of -1 could be negative π, in which case the leading sign on this last expression should be flipped from positive to negative. But empirical evidence tells us that only the positive sign is relevant to this problem.)
Gravitational Potential due to a Circular Torus
|
Evaluation of Elliptic Integrals
We use the Numerical Recipes algorithms to evaluate elliptic integrals; and we have checked our use of these algorithms against printed tables of elliptic integrals found in my CRC handbook. Here are the relevant steps used in confirming the proper evaluation of these functions.
First, my CRC handbook adopts the following notation (evaluating the incomplete elliptic integral of the first kind):
|
<math>~F(k,\phi) = \int_0^\phi \frac{d\Phi}{\sqrt{1 - k^2 \sin^2\Phi}}</math> |
and |
<math>~ \theta = \sin^{-1}k \, . </math> |
Alternatively, in the Numerical Recipes algorithm, the two arguments of the incomplete elliptic integral of the first kind are, <math>~\mathrm{ellf}(\phi, k)</math>, where the relevant function expression is,
|
<math>~F(\phi,k)</math> |
<math>~=</math> |
<math>~ \int_0^\phi \frac{d\theta}{\sqrt{1 - k^2 \sin^2\theta}} \, , </math> |
and the argument, <math>~\phi</math>, is expected to be provided in radians, instead of in degrees.
Some example values are:
| Incomplete Elliptic Integrals of the First & Second Kind | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CRC's <math>~F(k,\phi)</math> (top); <math>~E(k,\phi)</math> (bottom) | Numerical Recipe's <math>~F(\phi,k)</math> (top); <math>~E(\phi,k)</math> (bottom) | ||||||||||||||||
| <math>~\theta ~~ \rightarrow</math> | 20° | 35° | 50° | 65° | 80° | <math>~k ~~ \rightarrow</math> | 0.34202014 | 0.57357644 | 0.76604444 | 0.90630779 | 0.98480775 | ||||||
| <math>~\phi</math> | <math>~\phi</math> (radians) |
||||||||||||||||
| 11° | 0.1921 0.1918 |
0.1924 0.1916 |
0.1927 0.1913 |
0.1930 0.1910 |
0.1931 0.1908 |
0.19198622 | 0.192123431 0.191849180 |
0.192373471 0.191600363 |
0.192679935 0.191296982 |
0.192961053 0.191020217 |
0.193140116 0.190844685 |
||||||
| 23° | 0.4027 0.4002 |
0.4049 0.3980 |
0.4078 0.3952 |
0.4105 0.3927 |
0.4123 0.3911 |
0.40142573 | 0.402656868 0.400201278 |
0.404940840 0.397964813 |
0.407815120 0.395213994 |
0.410528813 0.392680594 |
0.412298101 0.391061525 |
||||||
| 35° | 0.6151 0.6067 |
0.6231 0.5991 |
0.6336 0.5895 |
0.6441 0.5806 |
0.6513 0.5748 |
0.61086524 | 0.615064063 0.606716517 |
0.623082364 0.599066179 |
0.633639464 0.589516635 |
0.644149296 0.580570509 |
0.651323943 0.574768972 |
||||||
| 56° | 0.9930 0.9622 |
1.0250 0.9335 |
1.0725 0.8962 |
1.1285 0.8595 |
1.1743 0.8344 |
0.97738438 | 0.993020463 0.962159483 |
1.024993767 0.933452135 |
1.072482572 0.896220989 |
1.128479892 0.859487843 |
1.174295801 0.834363150 |
||||||
| 77° | 1.3788 1.3104 |
1.4554 1.2457 |
1.5867 1.1580 |
1.7909 1.0643 |
2.0653 0.9917 |
1.34390352 | 1.37884243 1.31035009 |
1.45540074 1.24566028 |
1.58672349 1.15795471 |
1.79094197 1.06431530 |
2.06528894 0.99170032 |
||||||
|
1.6200 1.5238 |
1.7312 1.4323 |
1.9356 1.3055 |
2.3088 1.1638 |
3.1534 1.0401 |
|
1.62002589 1.52379921 |
1.73124518 1.43229097 |
1.93558110 1.30553909 |
2.30878680 1.16382796 |
3.15338525 1.04011440 |
||||||
Integration Limits
We define the following terms that are functions only of the four principal model parameters, <math>~(a, Z_0, \varpi_t, r_t)</math>, and therefore can be treated as constants while carrying out the pair of nested integrals that determine <math>~q_0</math>.
Zone I:
In an accompanying discussion, we have derived the following integration limits; numerical values are given for the specific case, <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{4}, \tfrac{3}{4}, \tfrac{1}{4})</math>:
|
where,
|
<math>~\kappa</math> |
<math>~\equiv</math> |
<math>~ Z_0^2 + a^2 - (\varpi_t^2 - r_t^2) </math> |
<math>\rightarrow</math> |
<math>~ \frac{5^2}{2^4\cdot 3^2} \approx 0.17361111 </math> |
|
<math>~C</math> |
<math>~\equiv</math> |
<math>~1 + \biggl( \frac{2Z_0}{\kappa}\biggr)^2 ( \varpi_t^2 - r_t^2) </math> |
<math>\rightarrow</math> |
<math>~\frac{17 \cdot 1409}{5^4} \approx 38.3248 </math> |
|
<math>~\beta_\pm</math> |
<math>~\equiv</math> |
<math>~ - \frac{\kappa}{2} \biggl[ \frac{\varpi_t \mp r_t \sqrt{C}}{(\varpi_t + r_t)(\varpi_t - r_t)} \biggr] </math> |
<math>\rightarrow</math> |
<math>~ -~\frac{5^2}{2^6\cdot 3}\biggl[ 1\mp \sqrt{ \frac{17\cdot 1409}{3^2\cdot 5^4}} \biggr] </math> |
Notice that we have specified these integration limits such that, in going from the lower limit <math>~(\lambda_1)</math> to the upper limit <math>~(\Lambda_1)</math>, the value of <math>~\xi_1</math> monotonically increases. CAUTION: This statement is often not true. The quantity, <math>~\kappa</math>, changes signs, depending on whether <math>~(a^2 + Z_0^2) \gtrless (\varpi_t^2 -r_t^2)</math>. When <math>~\kappa</math> changes signs, the two quantities, <math>~\xi_1|_\mathrm{max}</math> and <math>~\xi_1|_\mathrm{min}</math> switch roles; specifically, <math>~\xi_1|_\mathrm{max}</math> becomes less than <math>~\xi_1|_\mathrm{min}</math> (or visa versa).
Also,
|
where, in addition to the quantities defined above,
|
<math>~\biggl(\frac{\varpi_i}{a}\biggr)_\pm</math> |
<math>~\equiv</math> |
<math>~\frac{\kappa}{2a^2}\cdot \frac{\mathrm{B}}{\mathrm{A}} \biggl[1 \pm \sqrt{1-\frac{AC}{B^2}} \biggr] </math> |
|
<math>~\mathrm{A}</math> |
<math>~\equiv</math> |
<math>~\biggl(\frac{Z_0}{a}\biggr)^2 + \biggl[\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}}\biggr]^2 </math> |
|
<math>~\mathrm{B}</math> |
<math>~\equiv</math> |
<math>~\biggl(\frac{2\varpi_t Z_0^2}{a\kappa}\biggr) - \biggl[\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}}\biggr] </math> |
Here, our desire also is to specify the integration limits such that <math>~\xi_2</math> monotonically increases in going from the lower limit <math>~(\gamma_1)</math> to the upper limit <math>~(\Gamma_1)</math>. In order to check to see if this is the case, let's test the limiting values of <math>~\xi_2</math> when we are considering a radial-coordinate value roughly midway between its limits, say, when <math>~\xi_1 = 1.1</math>. For this specific case, we find,
<math>~\Rightarrow ~~~ \xi_2\biggr|_- = 0.802600 \, .</math>
Hence, our ordering of the limits appears to be the one desired.
Zone II:
| Figure 5: Zone II | ||
|---|---|---|
| Definition | Schematic Example | Quantitative Example: Partial Volumes Identified |
| <math>~r_t > Z_0 > 0</math>and<math>~a < \varpi_t - \sqrt{r_t^2 - Z_0^2}</math> | ||
In an accompanying discussion, we have derived the following integration limits; example numerical values of various parameters are provided for the specific case where, <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{20}, \tfrac{3}{4}, \tfrac{1}{4})</math>. Note that,
|
<math>~\kappa</math> |
<math>~=</math> |
<math>~- \frac{1319}{2^4\cdot 3^2 \cdot 5^2} \approx -0.36639 \, ;</math> |
|
<math>~C</math> |
<math>~=</math> |
<math>~1 + \frac{2^5\cdot 3^6 \cdot 5^2}{(1319)^2} = \frac{2322961}{(1319)^2} \approx 1.33522 \, ;</math> |
|
<math>~\beta_+</math> |
<math>~=</math> |
<math>~\frac{1}{2^6\cdot 3^2\cdot 5^2} \biggl[3\cdot 1319 - \sqrt{2322961} \biggr] \approx 0.16895 \, ;</math> |
|
<math>~\beta_-</math> |
<math>~=</math> |
<math>~\frac{1}{2^6\cdot 3^2\cdot 5^2} \biggl[3\cdot 1319 + \sqrt{2322961} \biggr] \approx 0.38063 \, .</math> |
Partial Volume #II-1
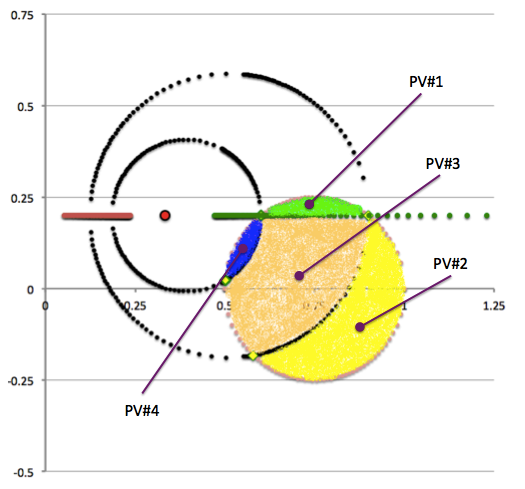
This is the green cropped-top sub-volume identified as Partial Volume #1 (PV#1) in the right-hand panel of Figure 5, and discussed in detail elsewhere.
|
|
Partial Volume #II-2
This is the sub-volume that is painted yellow and identified as Partial Volume #2 (PV#2) in the right-hand panel of Figure 5.
|
|
Partial Volume #II-3
This is the sub-volume that is painted orange and identified as Partial Volume #3 (PV#3) in the right-hand panel of Figure 5.
|
|
Partial Volume #II-4
This is the sub-volume that is painted blue and identified as Partial Volume #4 (PV#4) in the right-hand panel of Figure 5.
|
|
Summary (Zone II)
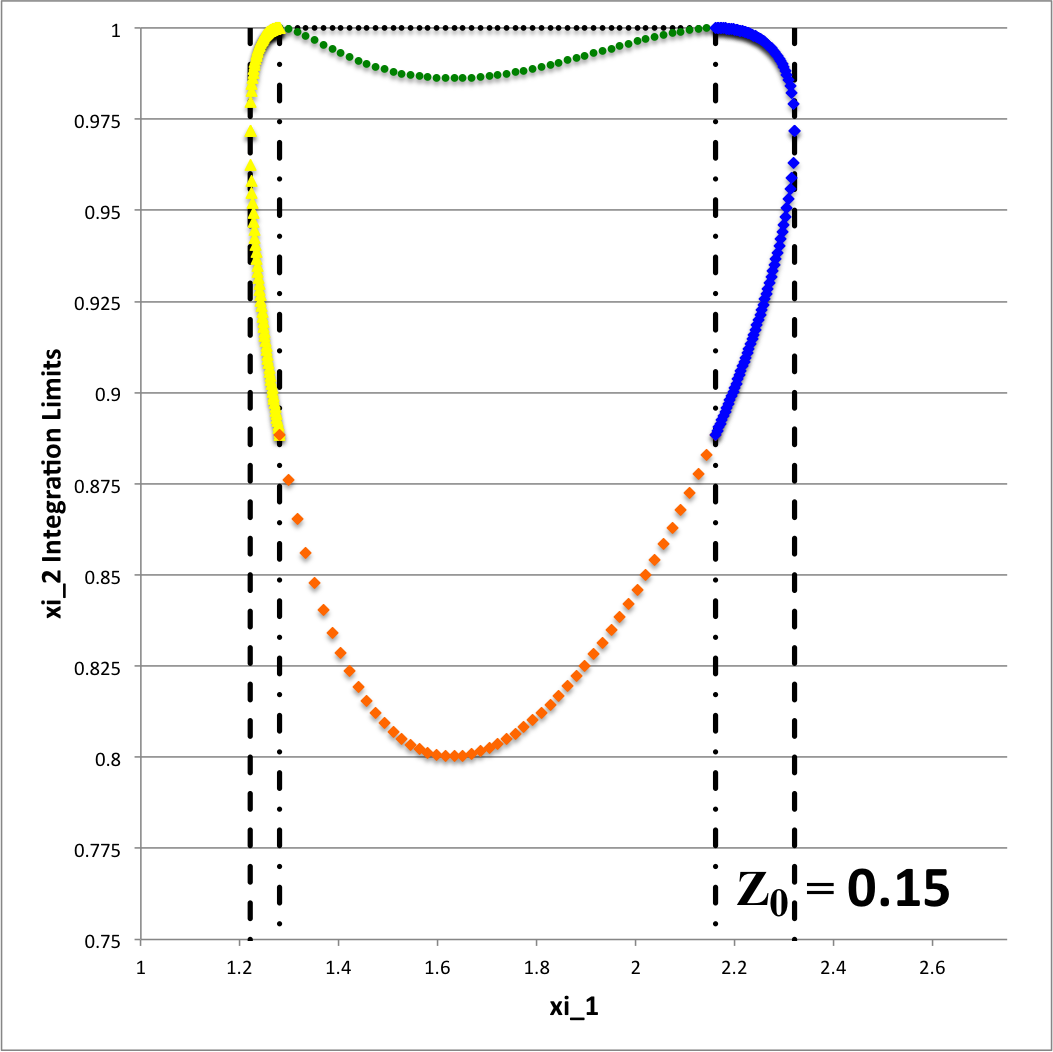
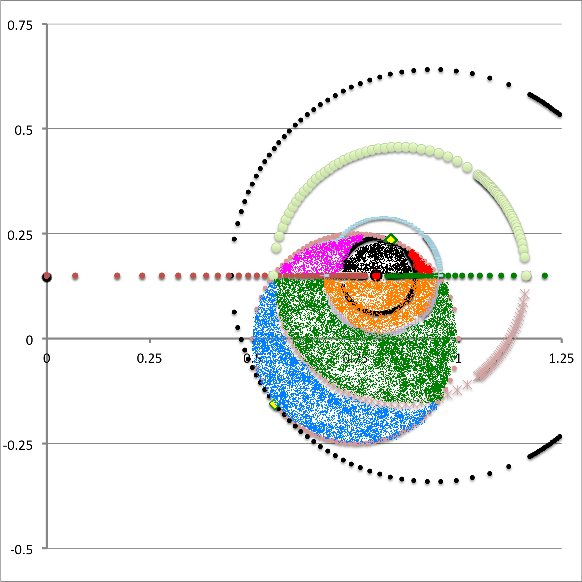
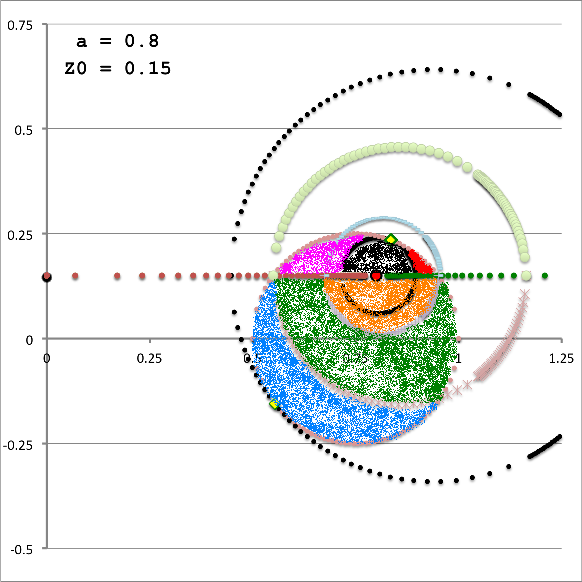
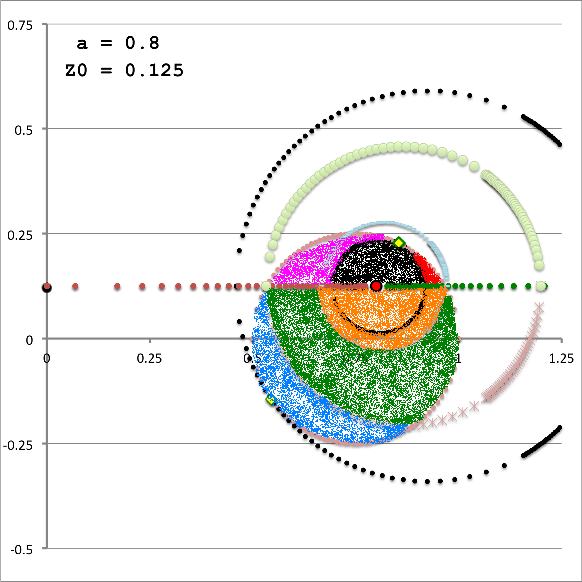
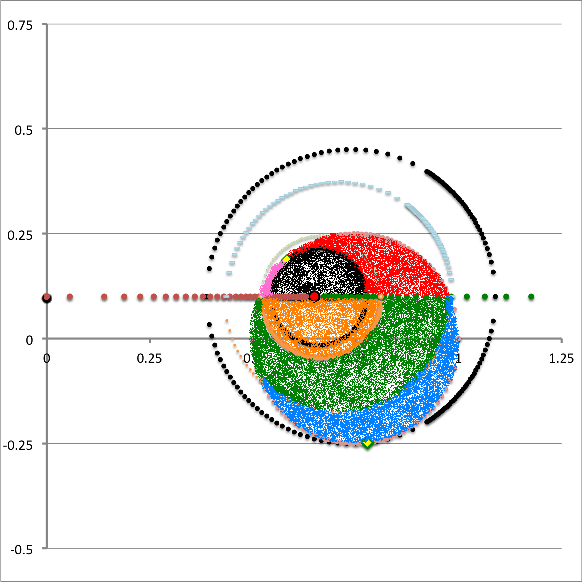
In summary, for a given set of the three model parameters <math>~(a, \varpi_t, r_t)</math> and the fourth, <math>~Z_0</math>, in the range, <math>~0 < Z_0 < r_t</math>, the volume of the (pink) circular torus is determined by adding together four partial volumes — that is, adding together the results of four separate 1D integrations over the "radial" toroidal coordinate <math>~(\xi_1)</math>. Although a total of eight radial integration limits (four lower limits and four upper limits) are required to fully determine the Zone II torus volume, only four unique limiting values need to be calculated because the partial volumes share <math>~\xi_1</math> boundaries. This has been illustrated by the black vertical dashed and dot-dashed lines in the left-hand panel of Figure 6 — and, drawing from the above discussion, the numerical values of these limits have been recorded in Table 1 — for the specific case of <math>~Z_0 = \tfrac{3}{20}</math>.
|
Table 1: Zone II Partial Volumes & Integration Limits on <math>~\xi_1</math>
for model parameters <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{20}, \tfrac{3}{4}, \tfrac{1}{4})</math> | ||||||||
|---|---|---|---|---|---|---|---|---|
| PV #1 | PV #2 | PV #3 | PV #4 | |||||
| IntegrationLimits | <math>~\lambda_1</math> | <math>~\Lambda_1</math> | <math>~\lambda_2</math> | <math>~\Lambda_2</math> | <math>~\lambda_3</math> | <math>~\Lambda_3</math> | <math>~\lambda_4</math> | <math>~\Lambda_4</math> |
| <math>2.16110</math> | <math>1.28080</math> | <math>1.28080</math> | <math>1.22088</math> | <math>2.16110</math> | <math>1.28080</math> | <math>2.32125</math> | <math>2.16110</math> | |
| VolumeFraction | 0.14237851 | 0.21569718 | 0.63537958 | 0.0065448719 | ||||
| Total Volume(nzones = 5000) | 1.00000014 <math>~\Rightarrow~</math> Error = -1.4E-7 | |||||||
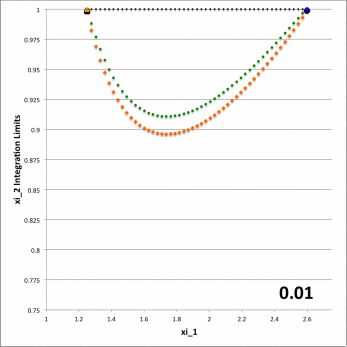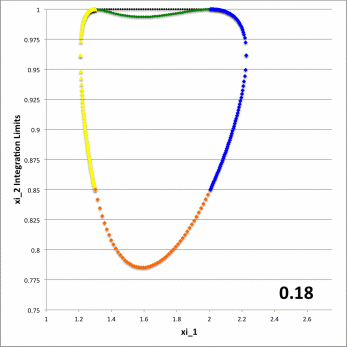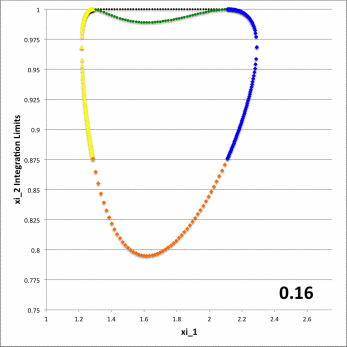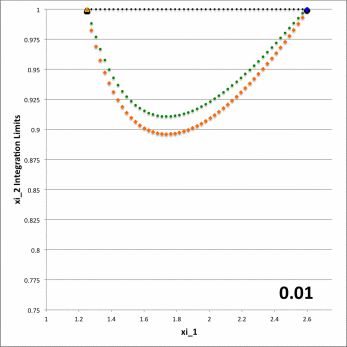
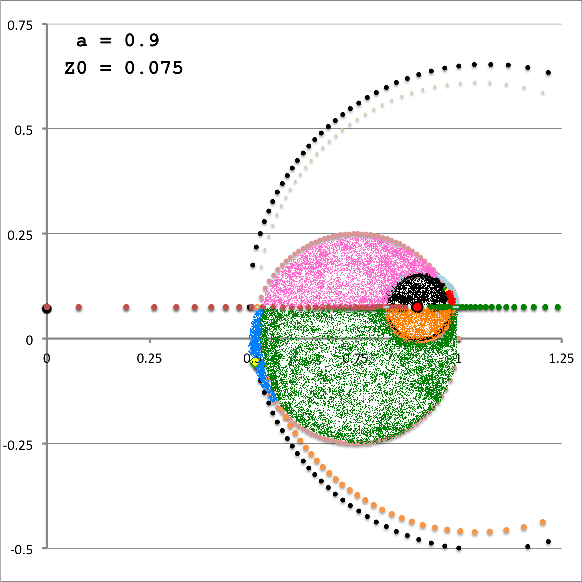
While the radial integrand expression for each partial volume is formally the same, it requires a specification of both limits, <math>~\gamma_i</math> and <math>~\Gamma_i</math>, for the "angular" coordinate integration which, as has also just been detailed, vary from one partial volume to the next and generally depend on the value of the radial coordinate. This dependence of the angular coordinate integration limits on the specific value of the radial coordinate across the four separate partial volumes is quantitatively illustrated in Figure 6 for the specific set of model parameters, <math>~(a, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{4}, \tfrac{1}{4})</math>, and for twenty-four different values of <math>~Z_0</math>.
|
Figure 6: Zone II Integration Limits on <math>~\xi_2</math>
for model parameters <math>~(a, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{4}, \tfrac{1}{4})</math> and various <math>~Z_0</math> | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||
In both panels of Figure 6, at each of a variety of values of the "radial" coordinate, <math>~\xi_1</math> (horizontal axis), a pair of colored dots identify the values (vertical axis) of the two "angular" coordinate integration limits, <math>~\gamma_i</math> (lower value) and <math>~\Gamma_i</math> (upper value). The left-hand panel has been constructed for the specific case, <math>~Z_0 = \tfrac{3}{20} = 0.15</math>; via an animation sequence, the right-hand panel shows how the limits vary with <math>~\xi_1</math> for twenty-four different values of <math>~Z_0</math> in the Zone II range <math>~(0 \leq Z_0 \leq r_t)</math>, as indicated in the lower right-hand corner of each frame. The limits identified by yellow dots must be fed into the radial integrand expression when evaluating partial volume #2 and the blue dots provide the limits for partial volume #4. Green dots identify the lower angular-coordinate integration limit across partial volume #1; orange dots identify the lower limit across partial volume #3; and the upper limit for both partial volume #1 and partial volume #3 is unity (black dots). Four vertical black lines (two dashed and two dot-dashed) have been added to the plot displayed in the left-hand panel of Figure 6 in order to emphasize that the boundaries between the four partial volumes are defined by the radial-coordinate integration limits, <math>~\lambda_i</math> and <math>~\Lambda_i</math>; as has been detailed in Table 1 for the specific case <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{20}, \tfrac{3}{4}, \tfrac{1}{4})</math>, the boundaries occur at <math>~\xi_1 = 1.22088, 1.28080, 2.16110,</math> and <math>~2.32125</math>.
Special Case of Z0 = 0
As has been recorded in an accompanying "Ramblings" appendix, my inversion of the toroidal-coordinate definitions — which, by default, incorporate the assumption that <math>~Z_0 = 0</math> — has led to the following expressions:
|
<math> ~\xi_1 </math> |
<math> ~= </math> |
<math> \frac{r(r^2 + 1)} {[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} \, , </math> |
|
<math> ~\xi_2 </math> |
<math> ~= </math> |
<math> \frac{r(r^2 - 1)}{[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} \, , </math> |
where,
<math> \chi \equiv \frac{\varpi}{a} ~~~;~~~\zeta\equiv\frac{z}{a} ~~~\mathrm{and} ~~~ r=(\chi^2 + \zeta^2)^{1/2} . </math>
It seems clear that, in this special case, the first radial coordinate that encounters the pink torus <math>~(\xi_1|_\mathrm{max})</math> should be given by the cylindrical-coordinate values, <math>~[\varpi,z] = [(\varpi_t - r_t),0]</math>; likewise the last radial coordinate <math>~(\xi_1|_\mathrm{min})</math> should be given by the cylindrical-coordinate values, <math>~[\varpi,z] = [(\varpi_t + r_t),0]</math>. Hence, in both limits, <math>~\zeta = 0 ~~ \Rightarrow ~~
r = \chi</math>, which further implies,
|
<math> ~\xi_1|_\mathrm{limits} </math> |
<math> ~= </math> |
<math> \frac{\chi(\chi^2 + 1)} {[\chi^2(\chi^2-1)^2 ]^{1/2}} = \frac{\chi^2 + 1} {\chi^2-1} \, . </math> |
Separately, then, we expect,
|
<math> ~\xi_1|_\mathrm{min} </math> |
<math> ~= </math> |
<math> \frac{(\varpi_t - r_t)^2 + a^2} {(\varpi_t - r_t)^2-a^2} \, , </math> |
|
<math> ~\xi_1|_\mathrm{max} </math> |
<math> ~= </math> |
<math> \frac{(\varpi_t + r_t)^2 + a^2} {(\varpi_t + r_t)^2-a^2} \, . </math> |
By comparison, the expressions that we have provided, above, for these two limits gives,
|
<math>~\biggl[ \xi_1|_\mathrm{max}\biggr]^{-2} </math> |
<math>~=</math> |
<math>~ 1-\biggl( \frac{a}{\varpi_t-\beta_+} \biggr)^2 \, , </math> |
|
<math>~\biggl[ \xi_1|_\mathrm{min} \biggr]^{-2} </math> |
<math>~=</math> |
<math>~ 1-\biggl( \frac{a}{\varpi_t-\beta_-} \biggr)^2 \, , </math> |
where, in the special case of <math>~Z_0 = 0</math>,
|
<math>~\kappa</math> |
<math>~=</math> |
<math>~ a^2 - (\varpi_t^2 - r_t^2) \, , </math> |
|
<math>~\beta_\pm</math> |
<math>~=</math> |
<math>~ - \frac{\kappa}{2} \biggl[ \frac{\varpi_t \mp r_t }{(\varpi_t + r_t)(\varpi_t - r_t)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2} \biggl[ (\varpi_t^2 - r_t^2) - a^2 \biggr] \biggl[ \frac{1 }{\varpi_t \pm r_t} \biggr] \, . </math> |
Hence,
|
<math>~\varpi_t - \beta_\pm</math> |
<math>~=</math> |
<math>~ \varpi_t - \frac{1}{2} \biggl[ (\varpi_t^2 - r_t^2) - a^2 \biggr] \biggl[ \frac{1 }{\varpi_t \pm r_t} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2(\varpi_t \pm r_t )} \biggl\{ 2\varpi_t(\varpi_t \pm r_t) - \biggl[ (\varpi_t^2 - r_t^2) - a^2 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2(\varpi_t \pm r_t )} \biggl\{ 2\varpi_t(\varpi_t \pm r_t) + \biggl[a^2 - (\varpi_t + r_t)(\varpi_t - r_t) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2} \biggl\{\frac{a^2}{(\varpi_t \pm r_t )} + 2\varpi_t - (\varpi_t \mp r_t) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{2} \biggl[\frac{a}{(\varpi_t \pm r_t )} + \frac{(\varpi_t \pm r_t)}{a} \biggr] </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\varpi_t - \beta_\pm}{a}\biggr)</math> |
<math>~=</math> |
<math>~ \biggl(\frac{\Upsilon_\pm^2 + a^2}{2a\Upsilon_\pm} \biggr) \, , </math> |
where,
|
<math>~\Upsilon_\pm</math> |
<math>~\equiv</math> |
<math>~\varpi_t \pm r_t \, .</math> |
This also means that,
|
<math>~1 - \biggl( \frac{a}{\varpi_t - \beta_\pm}\biggr)^2</math> |
<math>~=</math> |
<math>~ 1 - \biggl(\frac{2a\Upsilon_\pm}{\Upsilon_\pm^2 + a^2} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \frac{(\Upsilon_\pm^2 + a^2)^2 - 4a^2\Upsilon_\pm^2}{(\Upsilon_\pm^2 + a^2)^2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{\Upsilon_\pm^2 - a^2}{\Upsilon_\pm^2 + a^2} \biggr]^2 \, . </math> |
That is,
|
<math>~\biggl[ \xi_1|_\mathrm{max}\biggr]^{-2} = \biggl[ \frac{\Upsilon_+^2 - a^2}{\Upsilon_+^2 + a^2} \biggr]^2</math> |
<math>~\Rightarrow</math> |
<math>~\xi_1|_\mathrm{max} = \frac{\Upsilon_+^2 + a^2}{\Upsilon_+^2 - a^2} \, , </math> |
|
<math>~\biggl[ \xi_1|_\mathrm{min} \biggr]^{-2} = \biggl[ \frac{\Upsilon_-^2 - a^2}{\Upsilon_-^2 + a^2} \biggr]^2 </math> |
<math>~\Rightarrow</math> |
<math>~\xi_1|_\mathrm{min} = \frac{\Upsilon_-^2 + a^2}{\Upsilon_-^2 - a^2} \, . </math> |
Excellent! This matches the earlier supposition.
Also, given that <math>~C = 1</math> and <math>~A = B^2</math>, the pair of values, <math>~(\varpi_i/a)_\pm</math>, is degenerate and given by the expression,
|
<math>~\biggl(\frac{\varpi_i}{a}\biggr)_\pm</math> |
<math>~=</math> |
<math>~ \frac{\kappa}{2a^2 \mathrm{B}} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2a^2} \biggl[ (\varpi_t^2 - r_t^2) -a^2\biggr] \biggl[\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}}\biggr]^{-1} \, . </math> |
Hence,
|
<math>~\xi_2\biggr|_+</math> |
<math>~=</math> |
<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_+} </math> |
|
|
<math>~=</math> |
<math>~ \xi_1\biggl\{1 - \frac{ (\xi_1^2-1)^{1 / 2}}{\xi_1} \biggl[\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}}\biggr] 2a^2 \biggl[ (\varpi_t^2 - r_t^2) -a^2\biggr]^{-1} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \xi_1\biggl\{1 - \biggl[\biggl( \frac{\varpi_t}{a} \biggr)\frac{ (\xi_1^2-1)^{1 / 2}}{\xi_1} - 1 \biggr] 2a^2 \biggl[ (\varpi_t^2 - r_t^2) -a^2\biggr]^{-1} \biggr\} </math> |
Zone III
| Figure 7: Zone III | ||
|---|---|---|
| Definition | Schematic Example | Quantitative Example: Partial Volumes Identified |
|
<math>~r_t > Z_0 > 0</math>and
<math>~\varpi_t - \sqrt{r_t^2 - Z_0^2} < a < \varpi_t + \sqrt{r_t^2 - Z_0^2}</math>
<math>~\biggl[\frac{11}{20} < a < \frac{19}{20}\biggr]</math> |
||
Here, numerical values will be given for the specific case, <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{4}{5}, \tfrac{3}{20}, \tfrac{3}{4}, \tfrac{1}{4})</math>:
|
where,
|
<math>~\kappa</math> |
<math>~\equiv</math> |
<math>~ Z_0^2 + a^2 - (\varpi_t^2 - r_t^2) </math> |
<math>\rightarrow</math> |
<math>~\frac{13}{2^4\cdot 5} = 0.1625 </math> |
|
<math>~C</math> |
<math>~\equiv</math> |
<math>~1 + \biggl( \frac{2Z_0}{\kappa}\biggr)^2 ( \varpi_t^2 - r_t^2) </math> |
<math>\rightarrow</math> |
<math>\frac{457}{13^2} \approx 2.7041420 </math> |
|
<math>~\beta_\pm</math> |
<math>~\equiv</math> |
<math>~ - \frac{\kappa}{2} \biggl[ \frac{\varpi_t \mp r_t \sqrt{C}}{(\varpi_t + r_t)(\varpi_t - r_t)} \biggr] </math> |
<math>\rightarrow</math> |
<math>~ -~\frac{1}{2^6\cdot 5 }\biggl[ 39 \mp \sqrt{457} \biggr] </math> |
|
<math>~\Rightarrow~~~~\beta_+</math> |
<math>\approx</math> |
<math>~ -~0.055070130 </math> |
|
|
|
<math>~\beta_-</math> |
<math>\approx</math> |
<math>~ -~0.188679870 </math> |
|
|
Notice that we have specified these integration limits such that, in going from the lower limit <math>~(\lambda_1)</math> to the upper limit <math>~(\Lambda_1)</math>, the value of <math>~\xi_1</math> monotonically increases.
Partial Volume #III-1
This is the sub-volume that is painted blue and identified as Partial Volume #1 (PV#1) in the right-hand panel of Figure 7.
|
|
Partial Volume #III-2
This is the sub-volume that is painted green and identified as Partial Volume #2 (PV#2) in the right-hand panel of Figure 7.
|
|
Partial Volume #III-3
This is the sub-volume that is painted orange and identified as Partial Volume #3 (PV#3) in the right-hand panel of Figure 7.
|
|
Alternative determination of this partial volume: Notice that this "orange" meridional-plane segment is a (semi)circle whose cross-sectional radius is (see accompanying discussion),
<math>~r_\mathrm{orange} = \frac{a}{\sqrt{\lambda_3^2 - 1}} \, ,</math>
and it is associated with a circular torus whose major radius is,
<math>~R_\mathrm{orange} = \lambda_3 r_\mathrm{orange} \, .</math>
Hence, using the familiar expression for the volume of a circular torus, we know that the volume associated with this "orange" partial volume is,
|
<math>~V_\mathrm{orange}</math> |
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ 2\pi^2 R_\mathrm{orange} r_\mathrm{orange}^2 \biggr] = \pi^2 \lambda_3 r_\mathrm{orange}^3 = \frac{\pi^2 a^3 \lambda_3}{(\lambda_3^2-1)^{3/2}} </math> |
|
<math>~\Rightarrow~~~~\frac{V_\mathrm{orange}}{V_\mathrm{torus}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{a^3}{2\varpi_t r_t^2}\biggr) \frac{\lambda_3}{(\lambda_3^2-1)^{3/2}} \approx 0.165291952 \, .</math> |
Partial Volume #III-4
This is the sub-volume that is painted pink and identified as Partial Volume #4a (PV#4a) in the right-hand panel of Figure 7.
|
|
This is the sub-volume that is painted red and identified as Partial Volume #4b (PV#4b) in the right-hand panel of Figure 7.
|
|
Partial Volume #III-5
This is the sub-volume that is painted black and identified as Partial Volume #5 (PV#5) in the right-hand panel of Figure 7.
|
|
Alternative determination of this partial volume: Notice that this "black" meridional-plane segment is a (semi)circle whose cross-sectional radius is (see accompanying discussion),
<math>~r_\mathrm{black} = \frac{a}{\sqrt{\lambda_5^2 - 1}} \, ,</math>
and it is associated with a circular torus whose major radius is,
<math>~R_\mathrm{black} = \lambda_5 r_\mathrm{black} \, .</math>
Hence, using the familiar expression for the volume of a circular torus, we know that the volume associated with this "black" partial volume is,
|
<math>~V_\mathrm{black}</math> |
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ 2\pi^2 R_\mathrm{black} r_\mathrm{black}^2 \biggr] = \pi^2 \lambda_5 r_\mathrm{black}^3 = \frac{\pi^2 a^3 \lambda_5}{(\lambda_3^2-1)^{3/2}} </math> |
|
<math>~\Rightarrow~~~~\frac{V_\mathrm{black}}{V_\mathrm{torus}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{a^3}{2\varpi_t r_t^2}\biggr) \frac{\lambda_5}{(\lambda_5^2-1)^{3/2}} \approx 0.06988365 \, .</math> |
Summary (Zone III)
September 2017
Coming Up to Speed
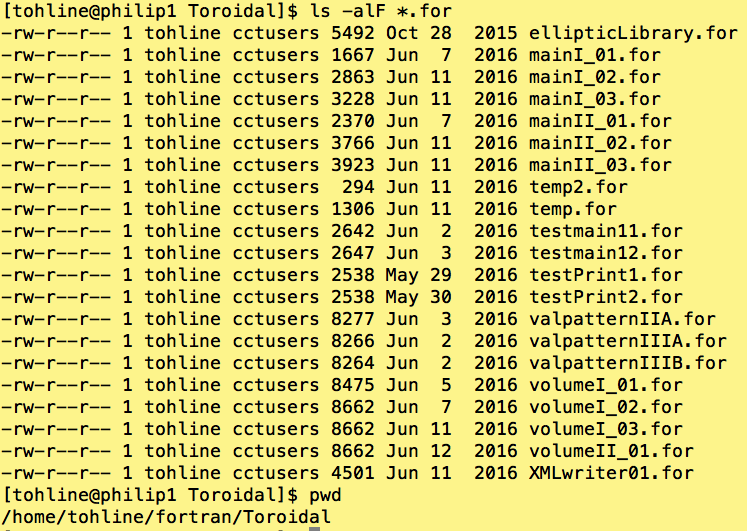
I am returning to this problem after letting it lay dormant for more than 14 months. These notes are being recorded as I try to decipher the fortran code that I have previously developed. Here is a screenshot from philip.hpc.lsu.edu that will help me archive the dates various fortran routines were last edited.
Let's start by reviewing the pair of routines (mainI_03.for,volumeI_03.for) which, presumably, integrate over the region labeled, Zone I, above.
Main Routine
| Unedited mainI_03.for | Current Comments & Notes |
|---|---|
June 12, 2016
ZoneI -- mainI_03.for
(Generates good Vistrails error map.)
========================================
PROGRAM MainI
real*8 dxx,dzz,dvarpi_t,dr_t,TorusPot,Volume,total,error
real*8 p3,p5
real*8 griddx,Xstart,Xend,Ystart,Yend,gridedge
real*8 x(49),y(49),xfull(50),yfull(50)
real*8 e(49,49),esum
real*8 elog
real emax,emin
real esumshort,elimit
real eshort(49,49),xshort(50),yshort(50)
integer iiZone,ngrid,i,j,k,ncount
151 format(1x,'Zone I:',5x,'Xstart, Xend, Ystart, Yend = ',&
&1P4d14.5)
152 format(1x,' j ',' k ',7X,'x',14X,'y',10X,'error')
153 format(2I5,1p3d15.6)
154 format(5x,'Across ',I6,' zones, the average error = ',1p1d15.2)
601 format(1x,'emax, emin = ',1p2E15.3)
dvarpi_t = 0.75d0
dr_t = 0.25d0
ngrid = 50
gridedge = 1.5d0
griddx = gridedge/dfloat(ngrid-1)
xfull(1)=0.0d0
yfull(1)=0.0d0
do i=2,ngrid
xfull(i) = xfull(i-1)+griddx
yfull(i) = yfull(i-1)+0.5d0*griddx
enddo
x(1)=0.5d0*griddx
y(1)=0.5d0*griddx
do i=2,ngrid-1
x(i) = x(i-1)+griddx
y(i) = y(i-1)+0.5d0*griddx
enddo
do j=1,ngrid-1
do k=1,ngrid-1
e(j,k)=0.0d0
enddo
enddo
!******
!
! Zone I
!
!******
! [iiZone = 0] Full Volume
!
iizone = 0
Xstart = 0.0d0
Xend = gridedge
Ystart = dr_t
Yend = y(ngrid-1)+0.5d0*griddx
write(*,151)Xstart,Xend,Ystart,Yend
write(*,152)
ncount=0
esum=0.0d0
do k=1,ngrid-1
do j=1,ngrid-1
if(x(j).gt.Xstart .and. x(j).lt.Xend)then
if(y(k).gt.Ystart .and. y(k).lt.Yend)then
dxx = x(j)
dzz = y(k)
total = 0.0d0
call Integrate(dxx,dzz,dvarpi_t,dr_t,iiZone,TorusPot,Volume,p3,p5)
e(j,k) = (1.0d0-Volume)
ncount=ncount+1
esum = esum + DABS(e(j,k))
write(*,153)j,k,x(j),y(k),e(j,k)
endif
endif
enddo
enddo
esum = esum/ncount
write(*,154)ncount,esum
! Prepare for XMLwriter
do k=1,ngrid
xshort(k) = xfull(k)
yshort(k) = yfull(k)
enddo
do k=1,ngrid-1
do j=1,ngrid-1
if(e(j,k).eq.0.0d0)e(j,k)=esum
enddo
enddo
do k=1,ngrid-1
do j=1,ngrid-1
elog = dlog10(DABS(e(j,k)))
eshort(j,k) = DABS(elog)
enddo
enddo
emax = 0.0
emin = 20.0
esumshort = esum
elimit = 1.5*esumshort
do k=1,ngrid-1
do j=1,ngrid-1
if(eshort(j,k).gt.emax)emax=eshort(j,k)
if(eshort(j,k).lt. emin)emin=eshort(j,k)
if(eshort(j,k).lt.elimit)eshort(j,k)=elimit
enddo
enddo
write(*,601)emax,emin
do k=1,ngrid-1
do j=1,ngrid-1
eshort(j,k) = (eshort(j,k)-elimit)/(emax-elimit)
enddo
enddo
emax = 0.0
emin = 20.0
do k=1,ngrid-1
do j=1,ngrid-1
if(eshort(j,k).gt.emax)emax=eshort(j,k)
if(eshort(j,k).lt. emin)emin=eshort(j,k)
enddo
enddo
write(*,601)emax,emin
do k=1,ngrid-1
do j=1,ngrid-1
eshort(j,k) = (eshort(j,k)-emin)/(emax-emin)
enddo
enddo
call XMLwriter01(ngrid,xshort,yshort,eshort)
stop
END PROGRAM MainI
|
|
Testing Volume Integration
| Unedited volumeI_03.for | Current Comments & Notes | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
subroutine Integrate(RR,ZZ,v_t,r_t,iiZone,TorusPot,sumVol,pieceIII3,pieceIII5)
!!!!!!!!!!!!
!
! Validate PATTERN III-B
!
!!!!!!!!!!!!
real*8 TorusPot,RR,ZZ,v_t,r_t
real*8 kappa,C,betaPlus,betaMinus
real*8 side,xi1Max,xi1Min
real*8 xi1Plus,xi1Minus,xiStart,xiEnd
real*8 grav,rho0,complete
real completeS,muSingle
real*8 Phi0,mu,coef,tempbeta,AAA,BBB
real*8 viPlus,viMinus,xi2Plus,xi2Minus,thetaMax,thetaMin
real*8 xx,ss,term1,darg1,darg2,tMax,tMin,sumPot
real arg1,arg2
real*8 volMax,volMin,sumVol,Vol0,tempsum
real*8 xi2One,xi2minOne,volOne,volminOne,volAdd
real*8 xi(5000),xihalf(4999)
real*8 pieceIII5,pieceIII3
integer n,idiag,nzones,iiZone
201 format(1x,'RR, ZZ, v_t, r_t:',1p4d13.5)
202 format(1x,'side, kappa, C, betaPlus, betaMinus, xi1Max, xi1Plus,&
& xi1Minus, xi1Min')
203 format(1x, 1p9d13.5)
idiag = 0
pii = 4.0d0*datan(1.0d0)
complete = pii/2.0d0
completeS = complete
grav = 1.0d0
rho0 = 1.0d0
Phi0 = 4.0d0*dsqrt(2.0d0)*grav*rho0*RR**2/3.0d0
Vol0 = 2.0d0*pii**2*v_t*r_t**2
side = (v_t**2 - r_t**2)
kappa = ZZ**2 + RR**2 - side
C = 1.0d0 + (2.0d0*ZZ/kappa)**2*side
betaPlus = -(kappa/2.0d0)*(v_t - r_t*dsqrt(C))/side
betaMinus = -(kappa/2.0d0)*(v_t + r_t*dsqrt(C))/side
|
|
|||||||||||||||||||||
if(kappa.le.0.0d0)xi1Max = 1.0d0/dsqrt(1.0d0-(RR/(v_t-betaPlus))**2)
if(kappa.gt.0.0d0)xi1Min = 1.0d0/dsqrt(1.0d0-(RR/(v_t-betaPlus))**2)
pieceIII5 = RR**3*xi1Min/(2.0d0*v_t*r_t**2*(xi1Min**2-1.0d0)**1.5)
if(kappa.le.0.0d0)xi1Min = 1.0d0/dsqrt(1.0d0-(RR/(v_t-betaMinus))**2)
if(kappa.gt.0.0d0)xi1Max = 1.0d0/dsqrt(1.0d0-(RR/(v_t-betaMinus))**2)
xi1Plus = 0.0d0
xi1Minus = 0.0d0
pieceIII3 = 0.0d0
if(r_t**2.ge.ZZ**2)then
xi1Plus = DABS(((v_t + dsqrt(r_t**2 - ZZ**2))**2 + RR**2)/ &
& ((v_t + dsqrt(r_t**2 - ZZ**2))**2 - RR**2))
endif
if(r_t**2.ge.ZZ**2)then
xi1Minus = DABS(((v_t - dsqrt(r_t**2 - ZZ**2))**2 + RR**2)/ &
& ((v_t - dsqrt(r_t**2 - ZZ**2))**2 - RR**2))
endif
if(r_t**2.ge.ZZ**2)then
pieceIII3 = RR**3*xi1Minus/(2.0d0*v_t*r_t**2*(xi1Minus**2-1.0d0)**1.5)
endif
! write(*,201)RR,ZZ,v_t,r_t
! write(*,202)
! write(*,203)side,kappa,C,betaPlus,betaMinus,xi1Max,xi1Plus,xi1Minus,xi1Min
|
<math>~\Rightarrow~~~\mathrm{pieceIII5} = \biggl(\frac{R^3 }{ 2\varpi_t r_t^2}\biggr) \biggl[ 1 - \frac{R^2}{(\varpi_t - \beta_-)^2} \biggr]^{-1 / 2} \biggl\{ \biggl[ 1 - \frac{R^2}{(\varpi_t - \beta_-)^2} \biggr]^{-1 / 2} - 1 \biggr\}^{- 3 / 2}</math>
|
|||||||||||||||||||||
! Begin 1D integration
! Specify sub-region...
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!
! On 29 May 2016, modified iiZone definition to correspond with
! online VisTrails chapter discussion:
! User:Tohline/2DStructure/ToroidalCoordinateIntegrationLimits
!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!
! ZONE II
! [iiZone = 1] Green cropped-top sub-volume
if(iiZone .eq. 1)then
xi1Start = xi1Minus
xi1End = xi1Plus
! [iiZone = 3] Lower (orange) Sub-volume that shares edge with
! Green cropped-top sub-volume
else if(iiZone .eq. 3)then
xi1Start = xi1Minus
xi1End = xi1Plus
! [iiZone = 4] (Blue) Segment to the left of Lower Sub-volume
else if(iiZone .eq. 4)then
xi1Start = xi1Min
xi1End = xi1Minus
! [iiZone = 2] (Yellow) Segment to the right of Lower Sub-volume
else if(iiZone .eq. 2)then
xi1Start = xi1Plus
xi1End = xi1Max
!
! ZONE III
! [iiZone = 31] (lightblue) Segment of Zone III
else if(iiZone .eq. 31)then
xi1End = xi1Max
xi1Start = xi1Plus
! [iiZone = 32] (darkgreen) Segment of Zone III
else if(iiZone .eq. 32)then
xi1End = xi1Plus
xi1Start = xi1Minus
! [iiZone = 33] (pink=4a) Segment of Zone III
else if(iiZone .eq. 33)then
xi1End = xi1Plus
xi1Start = xi1Min
! [iiZone = 34] (red=4b) Segment of Zone III
else if(iiZone .eq. 34)then
xi1End = xi1Minus
xi1Start = xi1Min
!
! ZONE I
! Full volume
else
xi1Start = xi1Min
xi1End = xi1Max
end if
! Finished specifying sub-region
|
Next comments. |
|||||||||||||||||||||
sumPot = 0.0d0
sumVol = 0.0d0
nzones = 1000
dxi = (xi1End-xi1Start)/dfloat(nzones-1)
xi(1) = xi1Start
do n=2,nzones
xi(n) = xi(n-1)+dxi
end do
do n=1,nzones-1
xihalf(n) = 0.5d0*(xi(n) + xi(n+1))
end do
! For each value of xi, evaluate these quantities
!!!!Diagnostics!!!!
303 format(1x,'arg1 = ',1pd15.7,/,&
& 1x,'arg2 = ',1pd15.7,/,&
& 1x,'tMax = ',1pd15.7,/)
304 format(1x,'arg1 = ',1pd15.7,/,&
& 1x,'arg2 = ',1pd15.7,/,&
& 1x,'tMin = ',1pd15.7,/)
403 format(1x,'arg1 = ',1pd15.7,/,&
& 1x,'volMax = ',1pd15.7,/)
404 format(1x,'arg1 = ',1pd15.7,/,&
& 1x,'volMin = ',1pd15.7,/)
405 format(1x,'TorusPot = ',1pd15.7,/,&
& 1x,'sum = ',1pd15.7,/,&
& 1x,'Vol0 = ',1pd15.7,/,&
& 1x,'sumVol = ',1pd15.7,/)
! If Z0 less than radius of torus, carry out double integration
do n=1,nzones-1
xx = xihalf(n)
! xx = xi(n)
ss = dsqrt(xx**2-1.0d0)
mu = dsqrt(2.0d0*ss/(ss+xx))
muSingle = mu
! coef = dsqrt(xx+1)*ellf(completeS,muSingle)/(ss**4*dsqrt(ss+xx))
coef = 1.0d0
tempbeta = v_t/RR - xx/ss
AAA = (ZZ/RR)**2 + tempbeta**2
BBB = 2.0d0*v_t*ZZ**2/(RR*kappa) - tempbeta
term1 = 1.0d0 - AAA*C/BBB**2
if(term1.lt.0.0d0)term1=0.0d0
viPlus = kappa*BBB/(2.0d0*RR**2*AAA)*(1.0d0+dsqrt(term1))
viMinus = kappa*BBB/(2.0d0*RR**2*AAA)*(1.0d0-dsqrt(term1))
xi2Plus = xx - ss/viPlus
xi2Minus = xx - ss/viMinus
thetaMax = dacos(xi2Plus)
thetaMin = dacos(xi2Minus)
darg2 = dsqrt(2.0d0/(1.0d0+xx))
arg2 = darg2
! Determine T(thetaMax)...
! darg1 = (pii - thetaMax)/2.0d0
! arg1 = darg1
! tMax = dsin(thetaMax)*(5.0d0*xx**2 - 4.0d0*xx*xi2Plus - 1.0d0)&
! & /(dsqrt(xx + 1.0d0)*dsqrt((xx-xi2Plus)**3))&
! & -4.0d0*xx*elle(arg1,arg2) + (xx-1.0d0)*ellf(arg1,arg2)
! write(*,310)ss,mu,tempbeta,AAA,BBB,viPlus,viMinus
310 format(1x,'ss, mu, tempbeta, AAA, BBB, viPlus, viMinus:',&
& /,1x,1p7d15.7)
! write(*,303)arg1,arg2,tMax
! Determine T(thetaMin)...
! darg1 = (pii - thetaMin)/2.0d0
! arg1 = darg1
! tMin = dsin(thetaMin)*(5.0d0*xx**2 - 4.0d0*xx*xi2Minus - 1.0d0)&
! & /(dsqrt(xx + 1.0d0)*dsqrt((xx-xi2Minus)**3))&
! & -4.0d0*xx*elle(arg1,arg2) + (xx-1.0d0)*ellf(arg1,arg2)
! write(*,304)arg1,arg2,tMin
!!
! sumPot = sumPot + dxi*coef*(tMax - tMin)
! TORUS VOLUME DETERMINATION...
xi2One = 1.0d0
xi2minOne = -1.0d0
! Determine Vol(thetaMax)...
volMax = dsqrt(1.0d0-xi2Plus**2)*(4.0d0*xx**2 - 3.0d0*xx*xi2Plus - 1.0d0)&
& /(ss**4*(xx-xi2Plus)**2)&
& + ((2.0d0*xx**2+1.0d0)/ss**5)*dacos((xx*xi2Plus - 1.0d0)/(xx-xi2Plus))
! Determine Vol(thetaMin)...
volMin = dsqrt(1.0d0-xi2Minus**2)*(4.0d0*xx**2 - 3.0d0*xx*xi2Minus - 1.0d0)&
& /(ss**4*(xx-xi2Minus)**2)&
& + ((2.0d0*xx**2+1.0d0)/ss**5)*dacos((xx*xi2Minus - 1.0d0)/(xx-xi2Minus))
! Determine Vol(One)...
volOne = 0.0
! volOne = dsqrt(1.0d0-xi2One**2)*(4.0d0*xx**2 - 3.0d0*xx*xi2One - 1.0d0)&
! & /(ss**4*(xx-xi2One)**2)&
! & + ((2.0d0*xx**2+1.0d0)/ss**5)*dacos((xx*xi2One - 1.0d0)/(xx-xi2One))
! Determine Vol(minusOne)...
volminOne = pii*((2.0d0*xx**2+1.0d0)/ss**5)
! volminOne = dsqrt(1.0d0-xi2minOne**2)*(4.0d0*xx**2 - 3.0d0*xx*xi2minOne - 1.0d0)&
! & /(ss**4*(xx-xi2minOne)**2)&
! & + ((2.0d0*xx**2+1.0d0)/ss**5)*dacos((xx*xi2minOne - 1.0d0)/(xx-xi2minOne))
! Specify sub-region...
! Full volume or similar segments ...
if(iiZone.eq.0 .or. iiZone.eq.2 .or. iiZone.eq.4)volAdd = volMax-volMin
! [iiZone = 1] Green cropped-top sub-volume
if(iiZone .eq. 1)volAdd = volOne - volMax
! [iiZone = 2] Lower (orange) Sub-volume that shares edge with Green cropped-top sub-volume
if(iiZone .eq. 3)volAdd = volOne-VolMin
! [iiZone = 31] Blue sub-volume of zone III
if(iiZone.eq.31)volAdd = volMax - volMin
! [iiZone = 32 ] Darkgreen Sub-volumes of zone III
if(iiZone .eq. 32)volAdd = volOne - volMin
! [iiZone = 33] Pink Sub-volumes of zone III
if(iiZone .eq. 33)volAdd = volOne - volMax
! [iiZone = 34] Red Sub-volume zone III
if(iiZone .eq. 34)volAdd = volMin - volminOne
sumVol = sumVol + dxi*volAdd
enddo
tempsum = sumVol
sumVol = pii*RR**3*sumVol/Vol0
! write(*,405)TorusPot,tempsum,Vol0,sumVol
return
end
|
Next comments. |
XML Writer for Visualization
| Unedited XMLwriter01.for | Current Comments & Notes |
|---|---|
Subroutine XMLwriter01(imax,x,y,cell_scalar)
real x(50),y(50),z(1)
real cell_scalar(49,49),point_scalar(50,50)
integer imax
integer extentX,extentY,extentZ
integer ix0,iy0,iz0
integer norm(50,3)
! imax=50
ix0=0
iy0=0
iz0=0
extentX=imax-1
extentY=imax-1
extentZ=0
z(1) = 0.0
! Set normal vector 1D array
do i=1,imax
norm(i,1)=0
norm(i,2)=0
norm(i,3)=1
enddo
! Set values of point_scalar array
do i=1,imax-1
do j=1,imax-1
point_scalar(i,j)=cell_scalar(i,j)
enddo
enddo
do i=1,imax-1
point_scalar(i,imax)=cell_scalar(i,imax-1)
enddo
do j=1,imax-1
point_scalar(imax,j)=cell_scalar(imax-1,j)
enddo
point_scalar(imax,imax)=point_scalar(imax-1,imax)
! End point_scalar definition
201 format('<?xml version="1.0"?>')
202 format('<VTKFile type="RectilinearGrid" version="0.1" byte_order="LittleEndian">')
302 format('</VTKFile>')
203 format(2x,'<RectilinearGrid WholeExtent="',6I3,'">')
303 format(2x,'</RectilinearGrid>')
204 format(4x,'<Piece Extent="',6I3,'">')
304 format(4x,'</Piece>')
205 format(6x,'<CellData Scalars="cell_scalars" Normals="magnify">')
305 format(6x,'</CellData>')
206 format(8x,'<DataArray type="Float32" Name="magnify" NumberOfComponents="3" format="ascii">')
207 format(8x,'<DataArray type="Float32" Name="cell_scalars" format="ascii">')
399 format(8x,'</DataArray>')
208 format(6x,'<PointData Scalars="colorful" Normals="direction">')
308 format(6x,'</PointData>')
209 format(8x,'<DataArray type="Float32" Name="colorful" format="ascii">')
210 format(6x,'<Coordinates>')
310 format(6x,'</Coordinates>')
211 format(8x,'<DataArray type="Float32" format="ascii" RangeMin="0" RangeMax="5">')
212 format(8x,'<DataArray type="Float32" format="ascii">')
213 format(8x,'<DataArray type="Float32" Name="direction" NumberOfComponents="3" format="ascii">')
501 format(10f9.5)
502 format(10f9.5)
503 format(5x,9(1x,3I2))
504 format(10f9.5)
505 format(5x,10(1x,3I2))
!!!!!
!
! Begin writing out XML tags.
!
!!!!!
write(*,201) !<?xml
write(*,202) !VTKFile
write(*,203)ix0,extentX,iy0,extentY,iz0,extentZ ! RectilinearGrid
write(*,204)ix0,extentX,iy0,extentY,iz0,extentZ ! Piece
write(*,205) ! CellData
write(*,207) ! DataArray(cell_scalars)
do j=1,imax-1
write(*,501)(cell_scalar(i,j),i=1,imax-1)
enddo
write(*,399) ! /DataArray
write(*,206) ! DataArray(cell_scalars)
do j=1,imax-1
write(*,503)(norm(i,1),norm(i,2),norm(i,3),i=1,imax-1)
enddo
write(*,399) ! /DataArray
write(*,305) ! /CellData
write(*,208) ! PointData
write(*,209) ! DataArray(points)
write(*,502)((point_scalar(i,j),j=1,imax),i=1,imax)
write(*,399) ! /DataArray
write(*,213) ! DataArray(cell_scalars)
do j=1,imax
write(*,505)(norm(i,1),norm(i,2),norm(i,3),i=1,imax)
enddo
write(*,399) ! /DataArray
write(*,308) ! /PointData
write(*,210) ! Coordinates
write(*,212) ! DataArray(x-direction)
write(*,504)(x(i),i=1,imax)
write(*,399) ! /DataArray
write(*,212) ! DataArray(y-direction)
write(*,504)(y(i),i=1,imax)
write(*,399) ! /DataArray
write(*,212) ! DataArray(z-direction)
write(*,504)z(1)
write(*,399) ! /DataArray
write(*,310) ! /Coordinates
write(*,304) ! /Piece
write(*,303) ! /RectilinearGrid
write(*,302) !/VTKFile
return
end
|
|
See Also
- Wikipedia's discussion of Toroidal Coordinates
- Determining the Gravitational Potential Using Toroidal Coordinates
- Ramblings Appendix Chapter: Determining the Relationships between Toroidal Coordinates and other Coordinate Systems

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |