User:Tohline/H BookTiledMenu

Tiled Menu

[Preamble by Joel E. Tohline — Circa 2020]  In an effort to serve ongoing research activities of the astrophysics community, this media-wiki-based hypertext book (H_Book) reviews what is presently understood about the structure, stability, and dynamical evolution of (Newtonian) self-gravitating fluids. In the context of this review, the "dynamical evolution" categorization generally will refer to studies that begin with an equilibrium configuration that has been identified — via a stability analysis — as being dynamically (or, perhaps, secularly) unstable then, using numerical hydrodynamic technique, follow the development to nonlinear amplitude of deformations that spontaneously develop as a result of the identified instability.

As is reflected in our choice of the overarching set of Principle Governing Equations, our focus is on studies of compressible fluid systems — those that obey a barotropic equation of state. But, in addition, chapters are included that review what is known about the structure and stability of self-gravitating incompressible (uniform-density) fluid systems because: (a) in this special case, the set of governing relations is often amenable to a closed-form, analytic solution; and (b) most modern computationally assisted studies of compressible fluid systems — both in terms of their design and in the manner in which results have been interpreted — have been heavily influenced by these, more classical, studies of incompressible fluid systems.

As the layout of the following tiled menu reflects, this review is broken into three major topical areas based primarily on geometrical considerations:

• Studies of configurations that are — at least initially — spherically symmetric.
• Two-dimensional configurations — such as rotationally flattened spheroidal-like or toroidal-like structures; or infinitesimally thin, but nonaxisymmetric, disk-like structures.
• Configurations that require a full three-dimensional treatment — most notably, "spinning" ellipsoidal-like structures; or binary systems.

This is very much a living review. The chosen theme encompasses an enormous field of research that, because of its relevance to the astrophysics community, over time is continuing to expand at a healthy pace. As a consequence the review is incomplete now, and it will always be incomplete, so please bear with me. On any given day/week/month I will turn my attention to a topic that seems particularly interesting to me and I will begin writing a new chapter or I will edit/expand the contents of an existing tiled_menu chapter. This necessarily means that all chapters are incomplete while, in practice, some are much more polished than others. Hopefully steady forward progress is being made and the review will indeed be viewed as providing a service to the community.

Context

Global Energy Considerations

Principal Governing Equations (PGEs)		Continuity		Euler		1st Law of Thermodynamics		Poisson

 

Equation of State (EOS)		Ideal Gas		Total Pressure   Bond, Arnett, & Carr (1984)

Spherically Symmetric Configurations

(Initially) Spherically Symmetric Configurations

 

		Structural Form Factors		Free-Energy of Spherical Systems

One-Dimensional PGEs

Equilibrium Structures

1D STRUCTURE

 

		Scalar Virial Theorem

Hydrostatic Balance Equation		<math>~\frac{dP}{dr} = - \frac{GM_r \rho}{r^2}</math>		Solution Strategies

 

Uniform-Density Sphere

 

Isothermal Sphere		<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>		via Direct Numerical Integration

 

Isolated Polytropes		Lane (1870)		<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>		Known Analytic Solutions		via Direct Numerical Integration		via Self-Consistent Field (SCF) Technique

 

Zero-Temperature White Dwarf		Chandrasekhar Limiting Mass (1935)

 

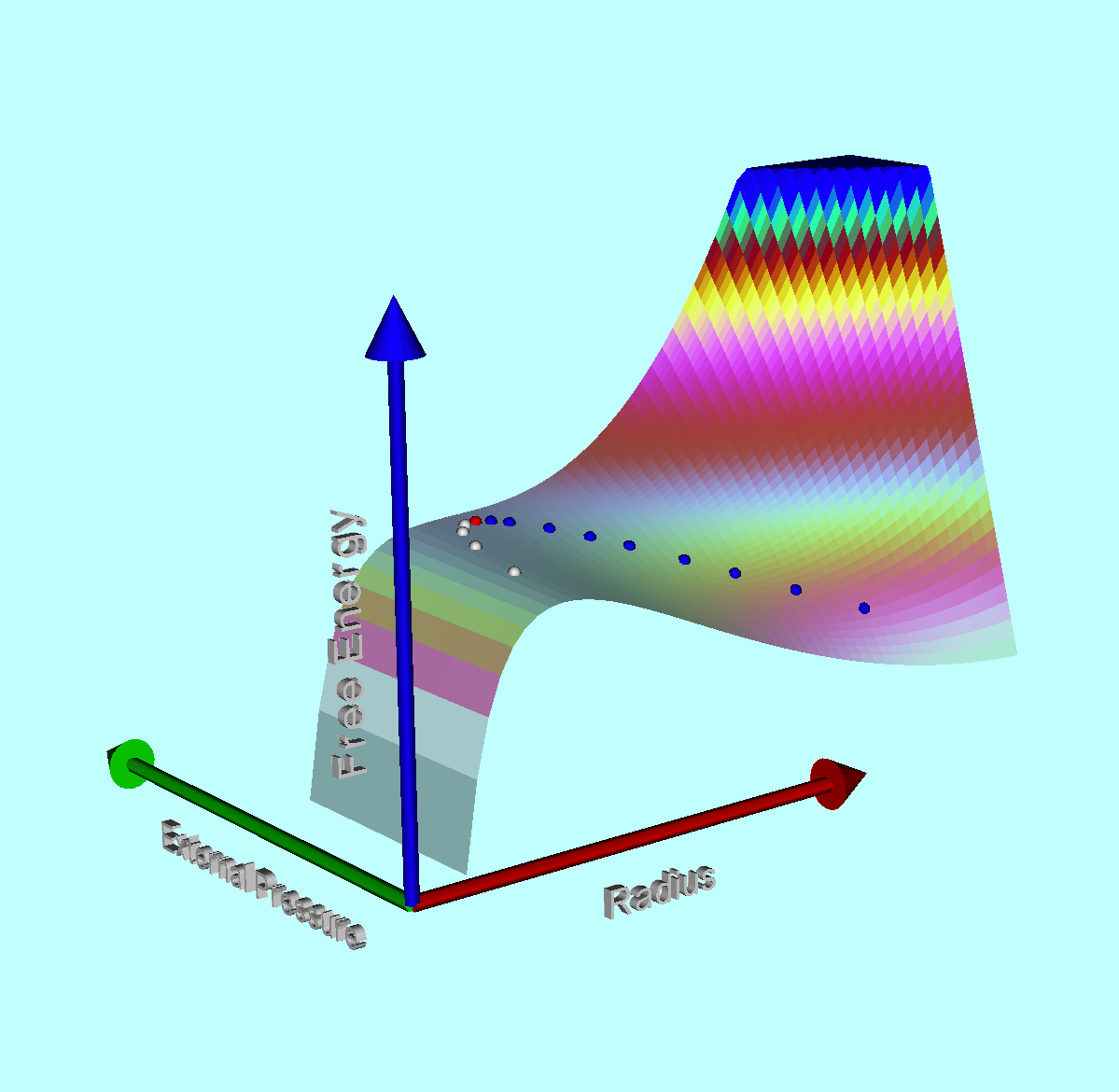
Virial Equilibrium of Pressure-Truncated Polytropes

Pressure-Truncated Configurations		Bonnor-Ebert (Isothermal) Spheres (1955 - 56)		Polytropes		Equilibrium Sequence Turning-Points ♥				Turning-Points (Broader Context)

 

Free Energy of Bipolytropes (nc, ne) = (5, 1)

Composite Polytropes (Bipolytropes)		Milne (1930)		Schönberg- Chandrasekhar Mass (1942)		Analytic (nc, ne) = (5, 1)		Analytic (nc, ne) = (1, 5)

 

Stability Analysis

1D STABILITY

 

		Variational Principle

Radial Pulsation Equation		Example Derivations & Statement of Eigenvalue Problem		(poor attempt at) Reconciliation		Relationship to Sound Waves

 

Jeans (1928) or Bonnor (1957)		Ledoux & Walraven (1958)		Rosseland (1969)

 

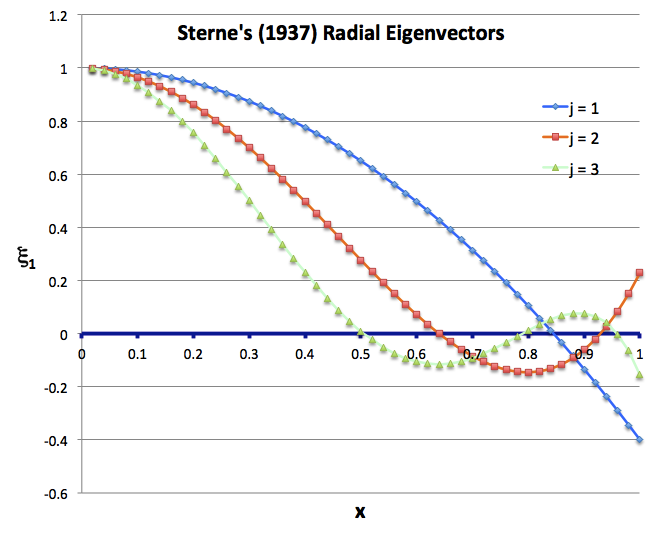
Uniform-Density Configurations		Sterne's Analytic Sol'n of Eigenvalue Problem (1937)

 

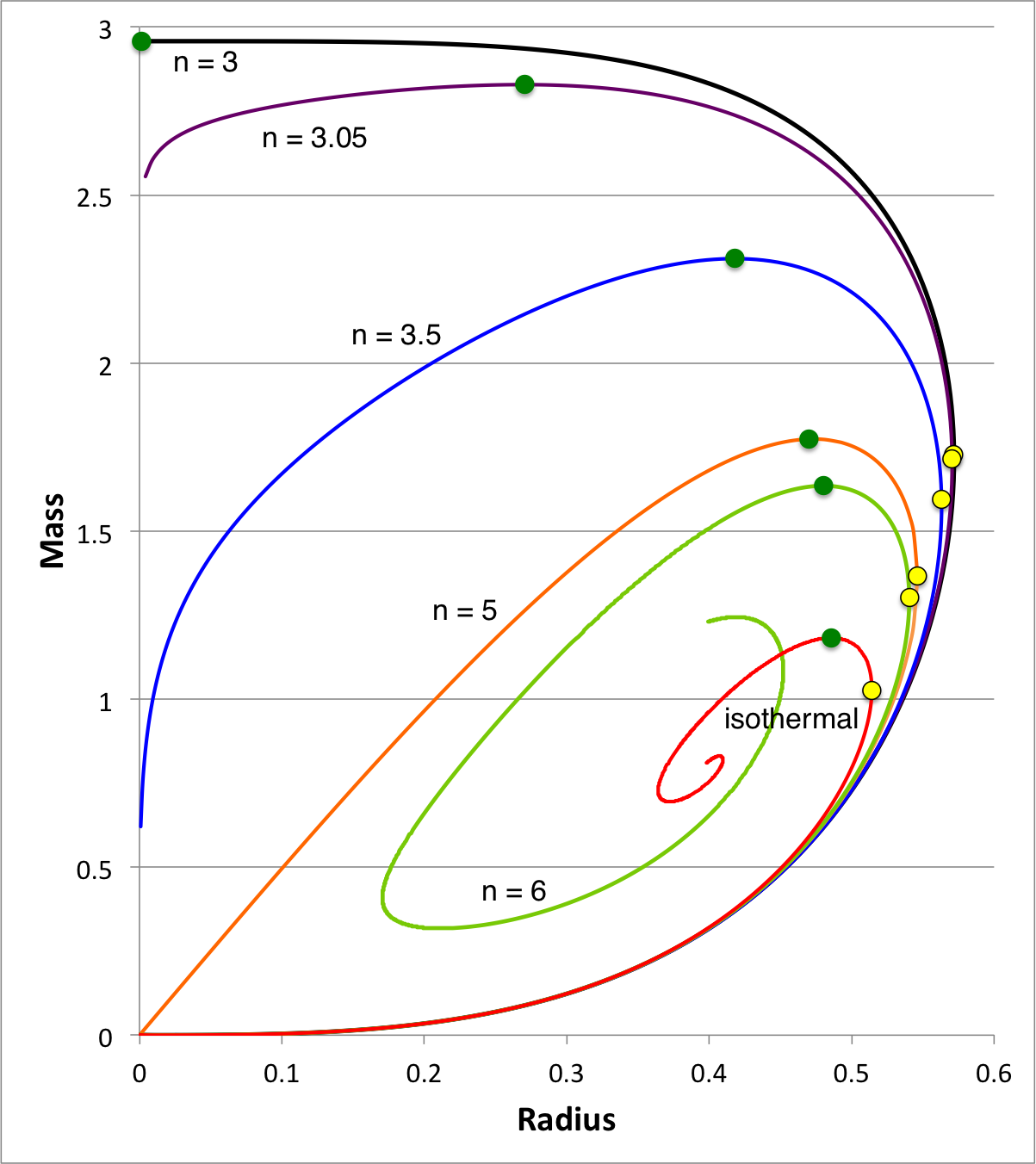
Pressure-Truncated Isothermal Spheres		<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math> where:    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>		via Direct Numerical Integration

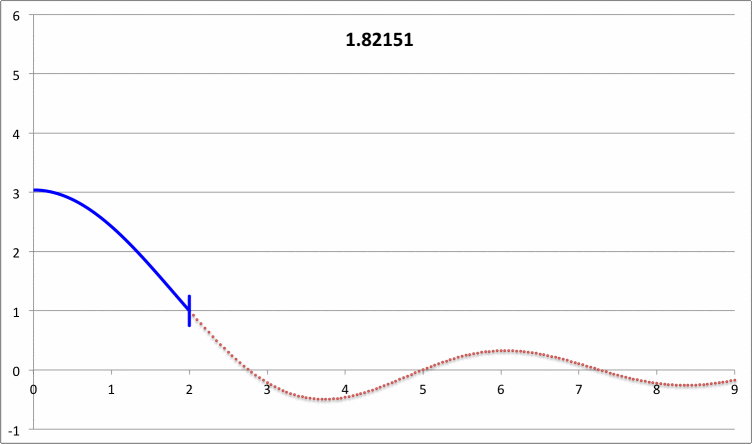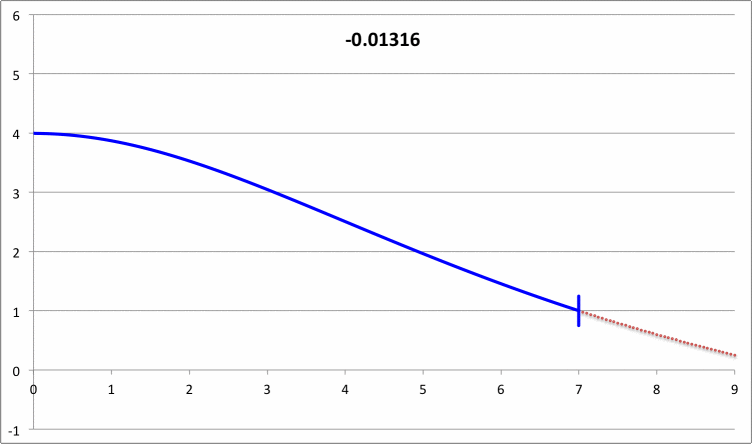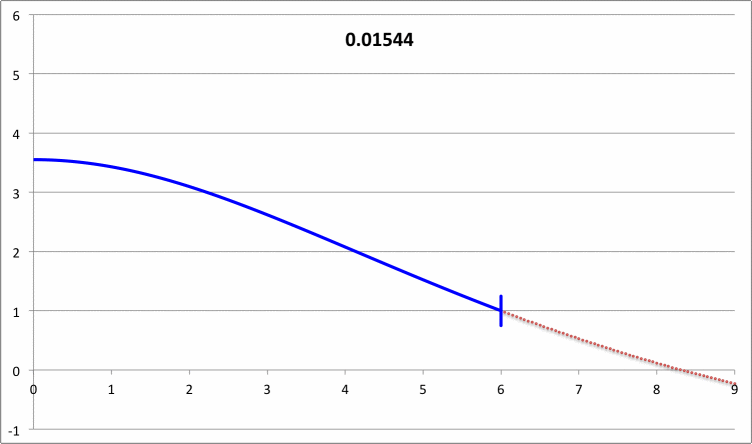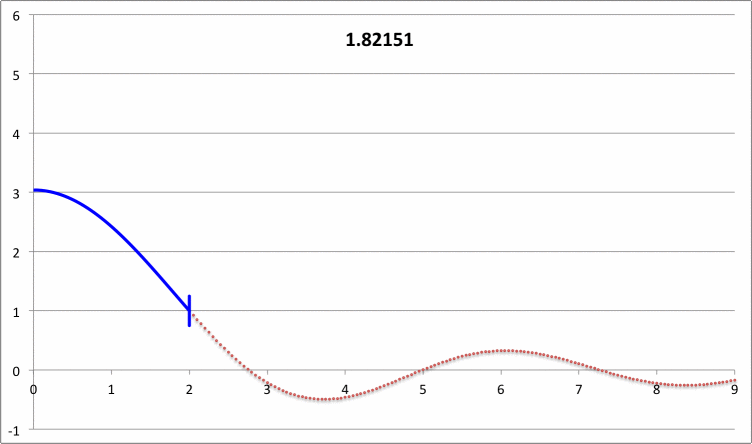
Yabushita's Analytic Sol'n for Marginally Unstable Configurations (1974)		<math>~\sigma_c^2 = 0 \, , ~~~~\gamma_\mathrm{g} = 1</math>  and   <math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} </math>

 

Polytropes		<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math> where:    <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math>    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>		Isolated n = 3 Polytrope				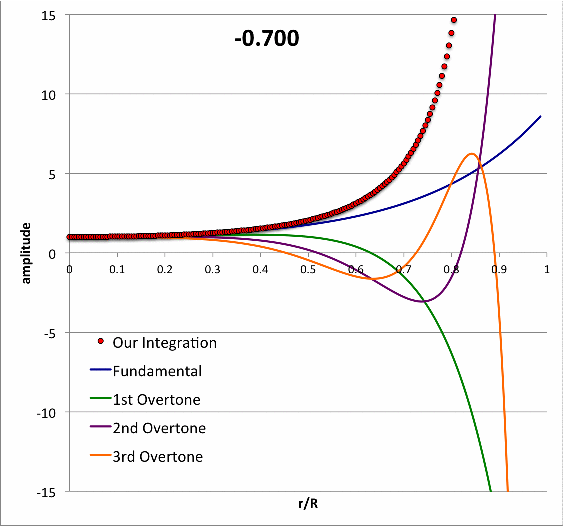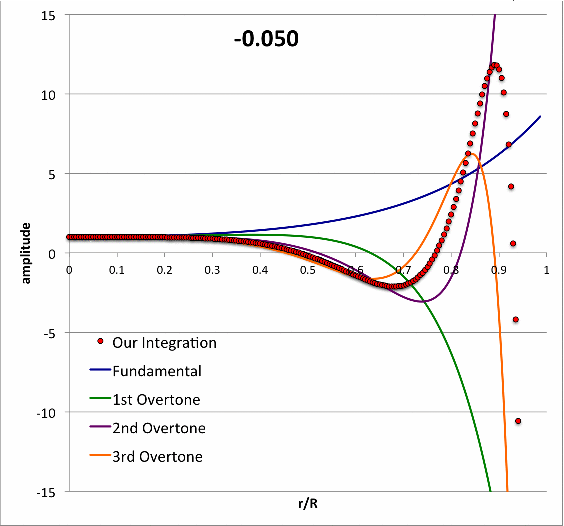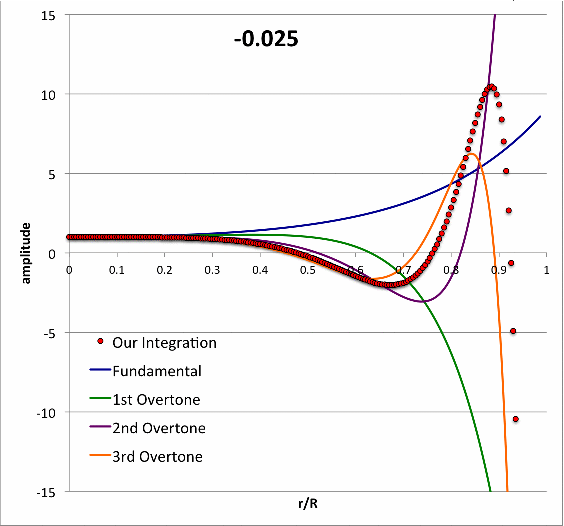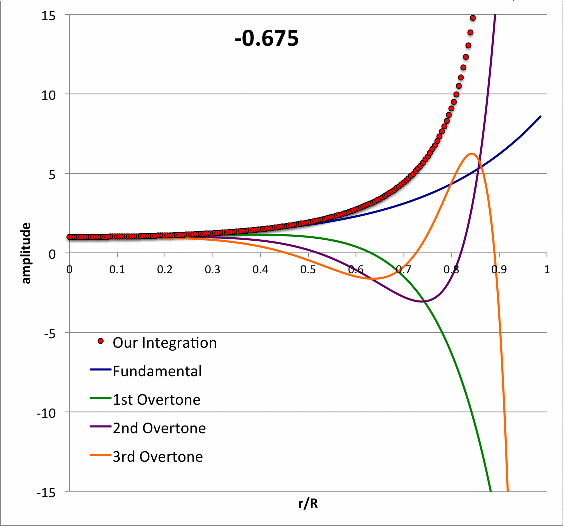Pressure-Truncated n = 5 Configurations

Exact Demonstration of B-KB74 Conjecture		Exact Demonstration of Variational Principle		Pressure-Truncated n = 5 Polytropes

Our Analytic Sol'n for Marginally Unstable Configurations (2017) ♥		<math>~\sigma_c^2 = 0 \, , ~~~~\gamma_\mathrm{g} = (n+1)/n</math>  and   <math>~x = \frac{3(n-1)}{2n}\biggl[1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\xi \theta^{n}}\biggr) \frac{d\theta}{d\xi}\biggr] </math>

 

BiPolytropes		Murphy & Fiedler (1985b) (nc, ne) = (1,5)		Our Broader Analysis

 

Nonlinear Dynamical Evolution

1D DYNAMICS

 

Free-Fall Collapse

 

Collapse of Isothermal Spheres		via Direct Numerical Integration		Similarity Solution

 

Collapse of an Isolated n = 3 Polytrope

 

Two-Dimensional Configurations (Axisymmetric)

(Initially) Axisymmetric Configurations

 

Storyline

 

PGEs for Axisymmetric Systems

Axisymmetric Equilibrium Structures

2D STRUCTURE

 

Constructing Steady-State Axisymmetric Configurations		Axisymmetric Instabilities to Avoid		Simple Rotation Profiles		Hachisu Self-Consistent-Field [HSCF] Technique		Solving the Poisson Equation

 

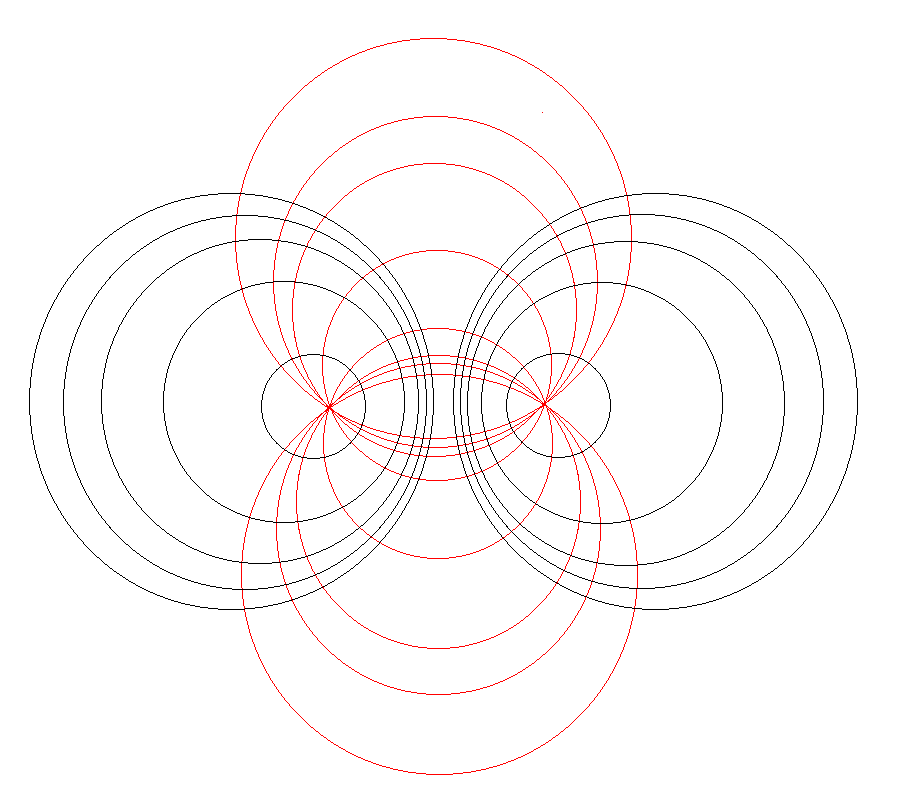
Using Toroidal Coordinates to Determine the Gravitational Potential				Attempt at Simplification ♥		Wong's Analytic Potential (1973)

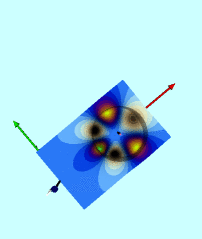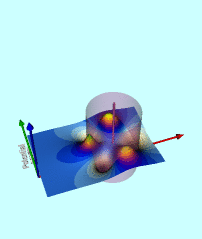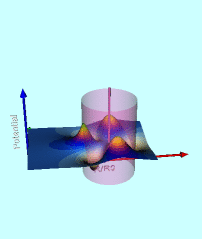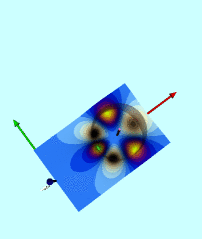
Spheroidal & Spheroidal-Like

Uniform-Density (Maclaurin) Spheroids		Maclaurin's Original Text & Analysis (1742)				Maclaurin Spheroid Sequence

 

Rotationally Flattened Isothermal Configurations		Hayashi, Narita & Miyama's Analytic Sol'n (1982)		Review of Stahler's (1983) Technique

 

Rotationally Flattened Polytropes		Example Equilibria

 

Rotationally Flattened White Dwarfs		Ostriker Bodenheimer & Lynden-Bell (1966)		Example Equilibria

Toroidal & Toroidal-Like

Definition: anchor ring

Massless Polytropic Configurations		Papaloizou-Pringle Tori (1984)

 

Self-Gravitating Incompressible Configurations		Dyson (1893)		Dyson-Wong Tori

 

Self-Gravitating Compressible Configurations		Ostriker (1964)

 

Stability Analysis

2D STABILITY

 

Sheroidal & Spheroidal-Like

Linear Analysis of Bar-Mode Instability		Bifurcation from Maclaurin Sequence		Traditional Analyses

 

• T. G. Cowling & R. A. Newing (1949), ApJ, 109, 149: The Oscillations of a Rotating Star
• M. J. Clement (1965), ApJ, 141, 210: The Radial and Non-Radial Oscillations of Slowly Rotating Gaseous Masses
• P. H. Roberts & K. Stewartson (1963), ApJ, 137, 777: On the Stability of a Maclaurin spheroid of small viscosity
• C. E. Rosenkilde (1967), ApJ, 148, 825: The tensor virial-theorem including viscous stress and the oscillations of a Maclaurin spheroid
• S. Chandrasekhar & N. R. Lebovitz (1968), ApJ, 152, 267: The Pulsations and the Dynamical Stability of Gaseous Masses in Uniform Rotation
• C. Hunter (1977), ApJ, 213, 497: On Secular Stability, Secular Instability, and Points of Bifurcation of Rotating Gaseous Masses
• J. N. Imamura, J. L. Friedman & R. H. Durisen (1985), ApJ, 294, 474: Secular stability limits for rotating polytropic stars

The equilibrium models are calculated using the polytrope version (Bodenheimer & Ostriker 1973) of the Ostriker and Mark (1968) self-consistent field (SCF) code … the equilibrium models rotate on cylinders and are completely specified by <math>~n</math>, the total angular momentum, and the specific angular momentum distribution <math>~j(m_\varpi)</math>. Here <math>~m_\varpi</math> is the mass contained within a cylinder of radius <math>~\varpi</math> centered on the rotation axis. The angular momentum distribution is prescribed in several ways: (1) imposing strict uniform rotation; (2) using the same <math>~j(m_\varpi)</math> as that of a uniformly rotating spherical polybrope of index <math>~n^'</math> (see Bodenheimer and Ostriker 1973); and (3) using <math>~j(m_\varpi) \propto m_\varpi</math>, which we refer to as <math>~n^' = L</math>, <math>~L</math> for "linear."

• J. R. Ipser & L. Lindblom (1990), ApJ, 355, 226: The Oscillations of Rapidly Rotating Newtonian Stellar Models
• J. R. Ipser & L. Lindblom (1991), ApJ, 373, 213: The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects
• J. N. Imamura, J. L. Friedman & R. H. Durisen (2000), ApJ, 528, 946: Nonaxisymmetric Dynamic Instabilities of Rotating Polytropes. II. Torques, Bars, and Mode Saturation with Applications to Protostars and Fizzlers
• M. Shibata, S. Karino, & Y. Eriguchi (2003), MNRAS, 343, 619 - 626: Dynamical bar-mode instability of differentially rotating stars: effects of equations of state and velocity profiles
• G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche ellipsoids

 

Toroidal & Toroidal-Like

Defining the Eigenvalue Problem

 

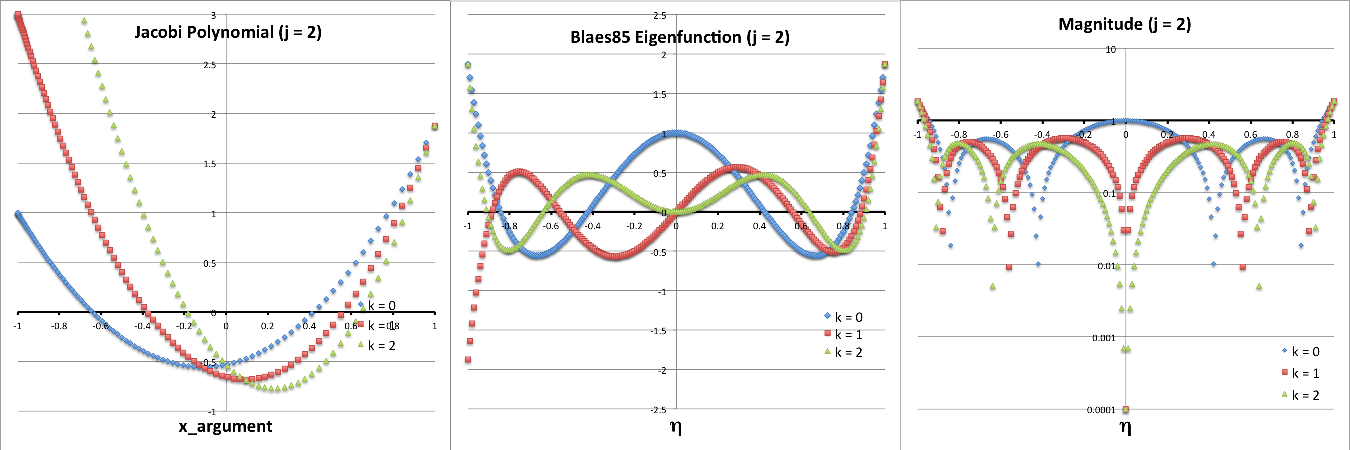
(Massless) Papaloizou-Pringle Tori		Analytic Analysis by Blaes (1985)

 

Self-Gravitating Polytropic Rings		Numerical Analysis by Tohline & Hachisu (1990)				Thick Accretion Disks (WTH94)

 

Nonlinear Dynamical Evolution

Sheroidal & Spheroidal-Like

2D DYNAMICS

 

Free-Fall Collapse of an Homogeneous Spheroid

 

Nonlinear Development of Bar-Mode		Initially Axisymmetric & Differentially Rotating Polytropes

 

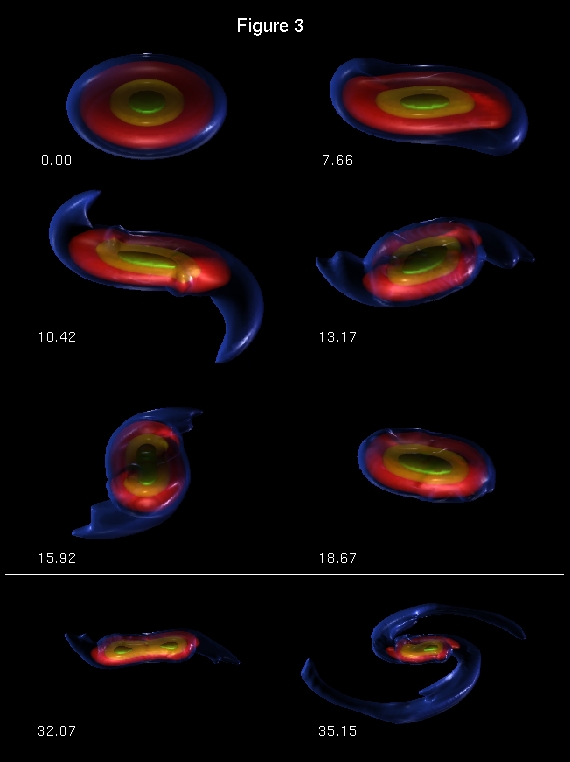
Two-Dimensional Configurations (Nonaxisymmetric Disks)

Infinitesimally Thin, Nonaxisymmetric Disks

 

2D STRUCTURE

 

Constructing Infinitesimally Thin Nonaxisymmetric Disks

 

Three-Dimensional Configurations

(Initially) Three-Dimensional Configurations

 

Equilibrium Structures

3D STRUCTURE

"One interesting aspect of our models … is the pulsation characteristic of the final central triaxial figure … our interest in the pulsations stems from a general concern about the equilibrium structure of self-gravitating, triaxial objects. In the past, attempts to construct hydrostatic models of any equilibrium, triaxial structure having both a high <math>~T/|W|</math> value and a compressible equation of state have met with very limited success … they have been thwarted by a lack of understanding of how to represent complex internal motions in a physically realistic way… We suggest … that a natural attribute of [such] configurations may be pulsation and that, as a result, a search for simple circulation hydrostatic analogs of such systems may prove to a fruitless endeavor.

— Drawn from §IVa of Williams & Tohline (1988), ApJ, 334, 449

Special numerical techniques must be developed "to build three-dimensional compressible equilibrium models with complicated flows." To date … "techniques have only been developed to build compressible equilibrium models of nonaxisymmetric configurations for a few systems with simplified rotational profiles, e.g., rigidly rotating systems (Hachisu & Eriguchi 1984; Hachisu 1986), irrotational systems (Uryū & Eriguchi 1998), and configurations that are stationary in the inertial frame (Uryū & Eriguchi 1996)."

— Drawn from §1 of Ou (2006), ApJ, 639, 549

Ellipsoidal & Ellipsoidal-Like

Constructing Ellipsoidal & Ellipsoidal-Like Configurations

 

Steady-State Tensor Virial Equaitons

Uniform-Density Incompressible Ellipsoids		Jacobi Ellipsoids		Riemann S-Type Ellipsoids		Type I Riemann Ellipsoids		Riemann meets COLLADA & Oculus Rift S

 

A Gauge Theory of Riemann Ellipsoids

 

Compressible Analogs of Riemann Ellipsoids		Thoughts

 

• B. P. Kondrat'ev (1985), Astrophysics, 23, 654: Irrotational and zero angular momentum ellipsoids in the Dirichlet problem
• D. Lai, F. A. Rasio & S. L. Shapiro (1993), ApJS, 88, 205: Ellipsoidal Figures of Equilibrium: Compressible models

Binary Systems

• S. Chandrasekhar (1933), MNRAS, 93, 539: The equilibrium of distorted polytropes. IV. the rotational and the tidal distortions as functions of the density distribution
• S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids

Roche's problem is concerned with the equilibrium and the stability of rotating homogeneous masses which are, further, distorted by the constant tidal action of an attendant rigid spherical mass.

 

Stability Analysis

3D STABILITY

 

Binary Systems

• S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids
• G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche Ellipsoids

Nonlinear Evolution

3D DYNAMICS

 

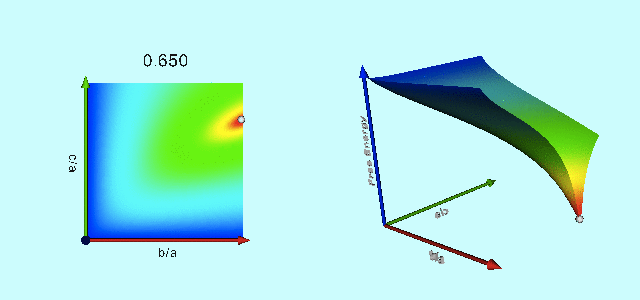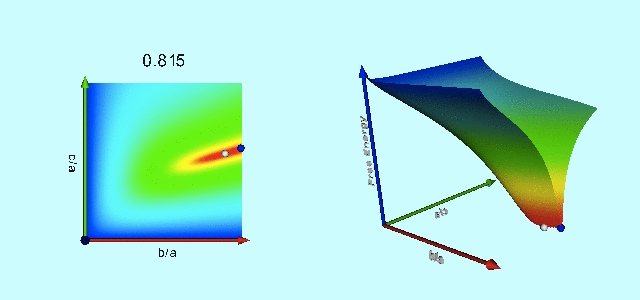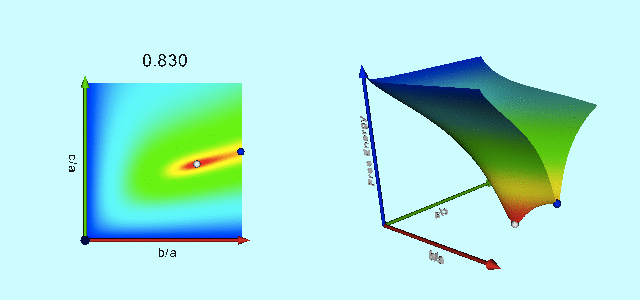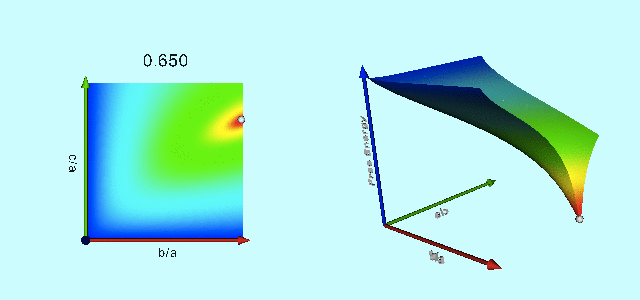
		Free-Energy Evolution from the Maclaurin to the Jacobi Sequence

Fission Hypothesis		"Fission" Simulations at LSU

 

Secular

• M. Fujimoto (1971), ApJ, 170, 143: Nonlinear Motions of Rotating Gaseous Ellipsoids
• W. H. Press & S. A. Teukolsky (1973), ApJ, 181, 513: On the Evolution of the Secularly Unstable, Viscous Maclaurin Spheroids
• S. L. Detweiler & L. Lindblom (1977), ApJ, 213, 193: On the evolution of the homogeneous ellipsoidal figures.

See Also

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation