Toroidal-Coordinate Integration Limits

In support of our accompanying discussion of the gravitational potential of a uniform-density circular torus, here we explain in detail what limits of integration must be specified in order to accurately determine the volume — and, hence also the total mass — of such a torus using toroidal coordinates.

Mapping from Cylindrical to Toroidal Coordinates

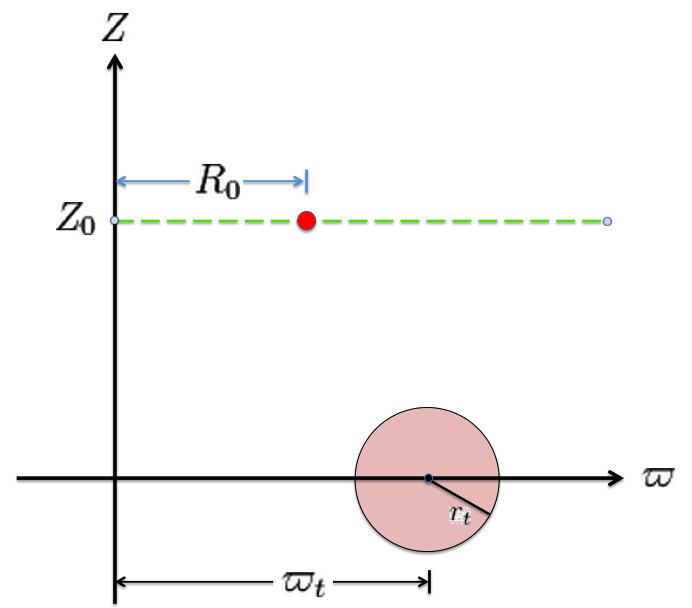
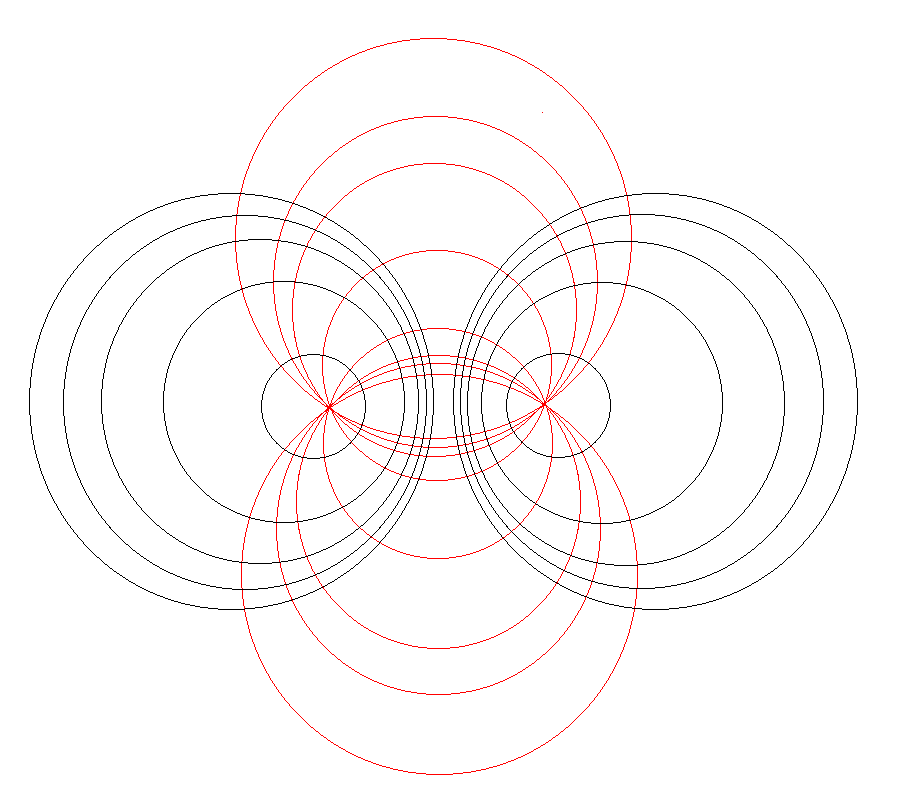
Referencing the illustration displayed in the left-hand panel of Figure 1, our goal is to determine the gravitational potential at any cylindrical-coordinate location <math>~(R_0, Z_0)</math> due to a uniform-density circular torus whose major radius is <math>~\varpi_t</math> and whose minor, cross-sectional radius is <math>~r_t</math>. Here we explain how a toroidal coordinate system <math>~(\xi_1, \xi_2)</math> — as defined, for example, by MF53 and as illustrated schematically in the right-hand panel of Figure 1 — can be used to reduce the geometric complexity of this problem. Note that, in our illustration, each black circle identifies a <math>\xi_1 = </math> constant surface and each red circle identifies a <math>\xi_2 = </math> constant surface. Note, as well, that the overall length scale (not labeled in our schematic diagram) is set by the distance, <math>~a</math>, from the vertical symmetry axis to the origin of the toroidal coordinate system — the point (actually, the axisymmetric ring) at which all the red circles intersect one another. Here we will show how, when using an appropriately aligned toroidal coordinate system, the three-dimensional, weighted integral over the mass distribution that is required to determine the gravitational potential at any location can be reduced to the sum of a small number (1 - 4) of one-dimensional integrals over the "radial" coordinate, <math>~\xi_1</math>.

Figure 1: Meridional slice through …
(Pink) Circular Torus	Toroidal Coordinate System (schematic) (see also Wikipedia's Apollonian Circles)

The pink circle represents the meridional cross-section through an axisymmetric, circular torus that lies in the equatorial plane of a cylindrical <math>~(\varpi, Z)</math>, coordinate system. The torus has a major axis of length, <math>~\varpi_t</math>, and a minor, cross-sectional radius of length, <math>~r_t</math>. The red circular dot identifies the cylindrical-coordinate location, <math>~(R_0, Z_0)</math>, at which the gravitational potential is to be evaluated.	As is explained more fully in Wikipedia's discussion of toroidal coordinates, rotating this two-dimensional bipolar coordinate system about the vertical axis produces a three-dimensional toroidal coordinate system. Black circles centered on the horizontal axis become circular tori — each identifying an axisymmetric, <math>\xi_1 =</math> constant surface; whereas, red circles centered on the vertical axis become spheres — each identifying an axisymmetric, <math>\xi_2 =</math> constant surface.

Special Case Alignment

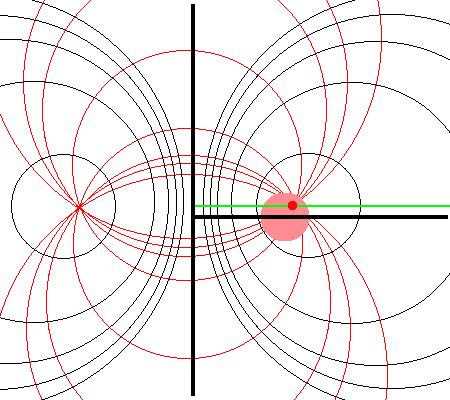
It should perhaps not be surprising to find that a toroidal coordinate system can be effectively used to quantitatively describe some properties — certainly the volume and possibly the gravitational potential — of circular tori because each <math>\xi_1 = </math> constant surface in a toroidal coordinate system (see the black circles in the right-hand panel of Figure 1) defines the surface of an axisymmetric, circular torus. In order to map from a cylindrical-coordinate representation of a circular torus (see the left-hand panel of Figure 1) to a toroidal-coordinate representation of that torus, at first glance it would seem reasonable to establish the alignment depicted schematically in Figure 2. That is, align the horizontal and vertical axes of the bipolar coordinate system (right-hand panel of Figure 1) with, respectively, the <math>\varpi-</math>axis and the <math>Z-</math>axis of the cylindrical coordinate system, then scale the overall size of the bipolar coordinate system until one <math>\xi_1 = </math> constant surface perfectly aligns with the surface of the (pink) torus.

Figure 2: Schematic Illustration of "Special Case" Alignment

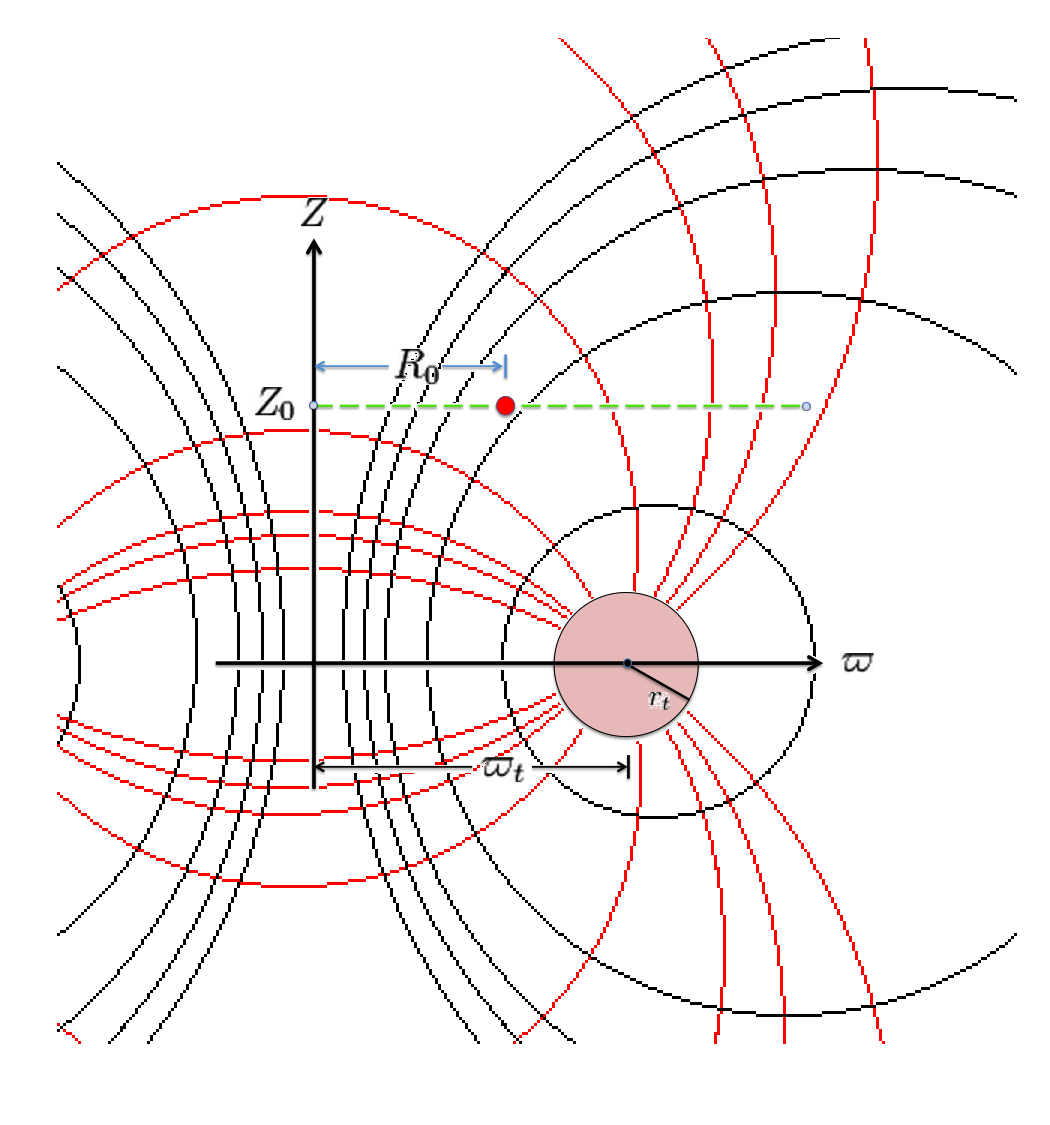
Here, a mapping from cylindrical coordinates to toroidal coordinates is achieved by aligning the horizontal and vertical axes of the bipolar coordinate system (right-hand panel of Figure 1) with, respectively, the <math>\varpi-</math>axis and the <math>Z-</math>axis of the cylindrical coordinate system, then scaling the overall size of the bipolar coordinate system, <math>~a</math>, until one <math>\xi_1 = </math> constant surface perfectly aligns with the surface of the (pink) torus.

This is the "special case" alignment that we have discussed in an accompanying chapter. It is achieved by setting the scale-length, <math>~a</math>, of the toroidal-coordinate system to a value given by the expression,

<math>~\sqrt{\varpi_t^2 - r_t^2}\, ,</math>

which means that the "radial" toroidal coordinate that aligns with the surface of the (pink) torus has the value,

<math>~\frac{\varpi_t}{r_t} \, .</math>

While the special alignment depicted in Figure 2 might at first glance seem reasonable, we have found that it does not generally enable us to transform the multi-dimensional integral expression for the gravitational potential into a one-dimensional integral over <math>~\xi_1</math>, as desired.

Practical Transformation

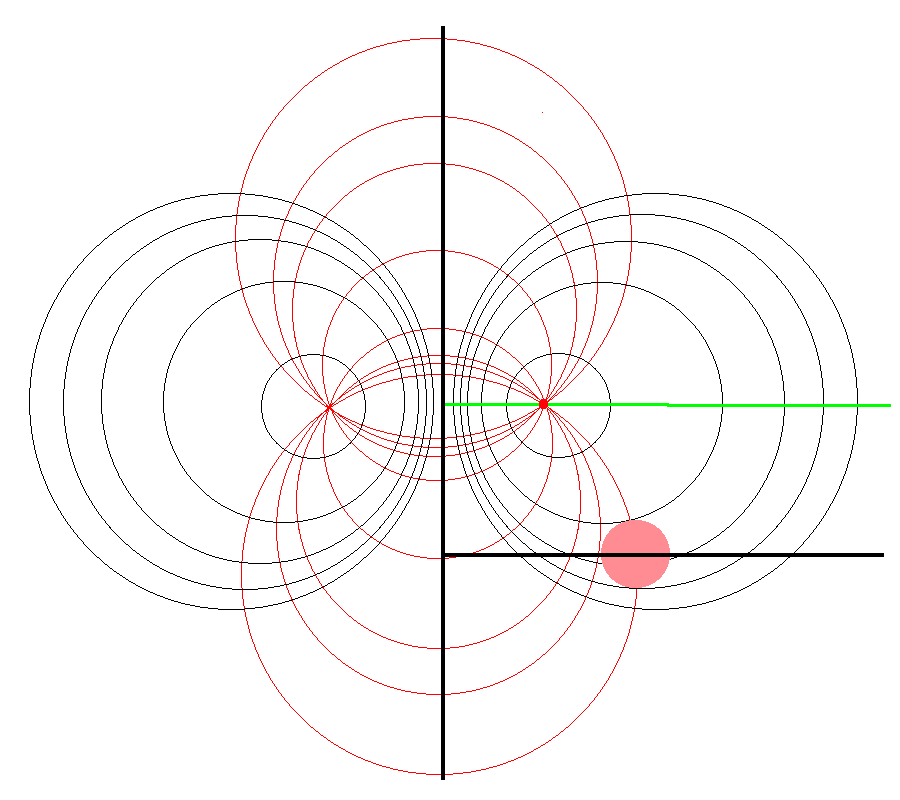
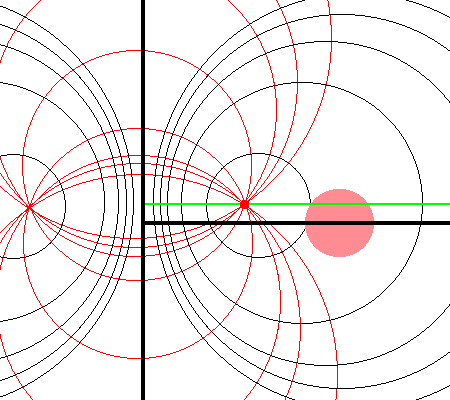
However, we have discovered that this desired transformation can be accomplished by shifting the toroidal-coordinate system vertically and scaling it such that its off-axis "origin" aligns with the cylindrical-coordinate location, <math>~(R_0, Z_0)</math>, at which the gravitational potential is to be evaluated. The left-hand panel of Figure 3 illustrates what results from aligning in this manner the left-hand and right-hand panels of Figure 1. The origin of the toroidal coordinate system sits on the green line-segment, a distance <math>~Z = Z_0</math> above the equatorial plane of the torus, and a distance <math>~a = R_0</math> from the symmetry axis.

Figure 3: Quantitative Illustration of Employed Toroidal Coordinate System

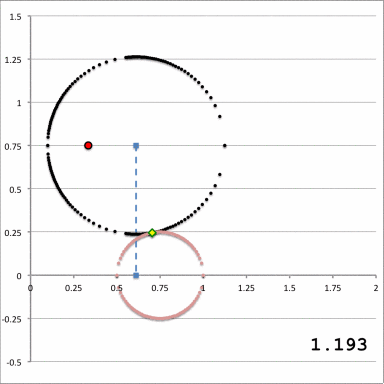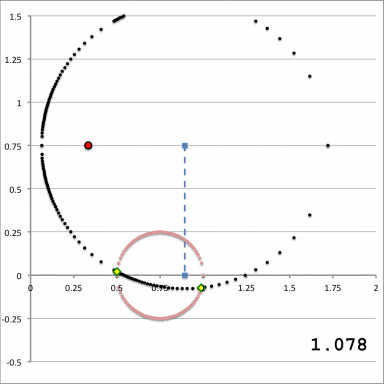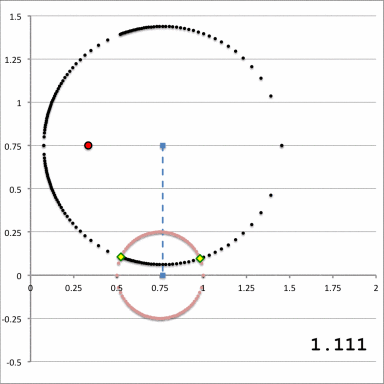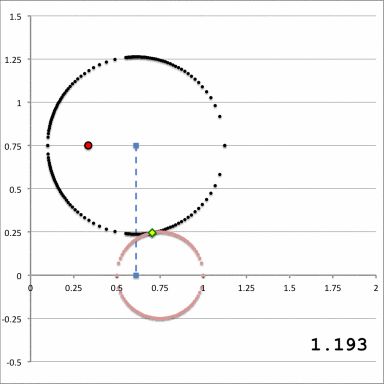
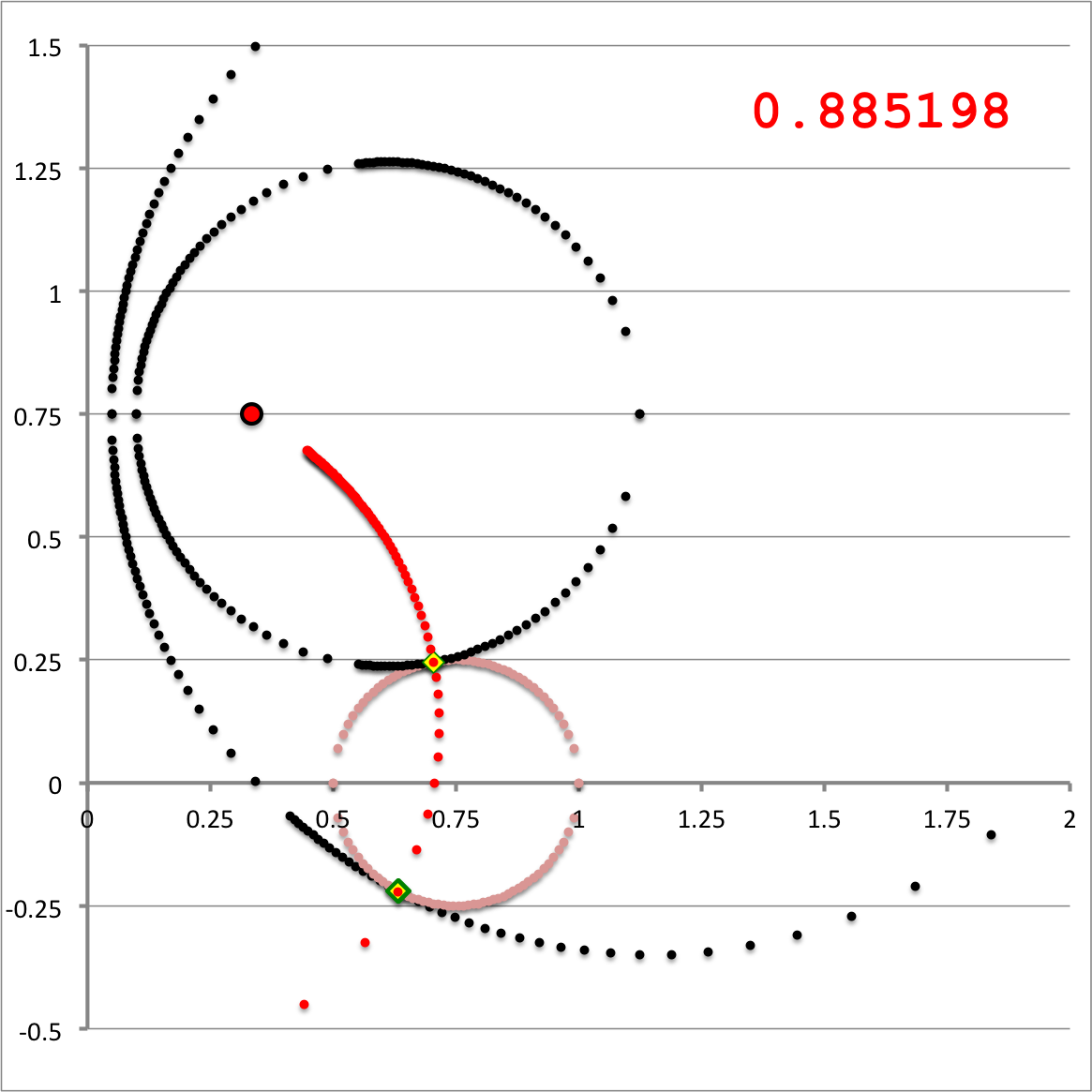
The middle and right-hand panels of Figure 3 display quantitatively how the boundary of the (pink) circular torus is defined in toroidal coordinates when an alignment of coordinate systems is made, as illustrated in the left-hand panel of Figure 3, for the parameter values: <math>~(R_0, Z_0) = (\tfrac{1}{3}, \tfrac{3}{4})</math> and <math>~(\varpi_t, r_t) = (\tfrac{3}{4}, \tfrac{1}{4})</math>. As the middle panel shows, black toroidal-coordinate circles intersect and/or thread through the (pink) torus for values of the radial coordinate in the range, <math>1.045 \leq \xi_1 \leq 1.193</math>. And, as the right-hand panel shows, the red toroidal-coordinate circle that corresponds to the angular-coordinate value, <math>~\xi_2 = 0.885198</math>, not only threads through the (pink) torus but identifies the "angle" at which the two limiting <math>\xi_1 =</math> constant circles touch the surface of the torus. The derivations that have led to the construction of these two figure panels are presented in an accompanying discussion.

One-Dimensional Integral Equations

Volume of Circular Torus

<math>~\frac{V_i}{V_\mathrm{torus}}</math>

<math>~\frac{a^3}{2\pi \varpi_t r_t^2} \int\limits_{\xi_1 = \lambda_i}^{\xi_1 = \Lambda_i} d\xi_1 \biggl\{ \frac{(1-\xi_2^2)^{1/2} [ 4\xi_1^2 - 3\xi_1 \xi_2 - 1]}{(\xi_1^2-1)^2 (\xi_1 - \xi_2)^2} + \biggl[ \frac{(2\xi_1^2 + 1)}{(\xi_1^2-1)^{5/2}}\biggr] \cos^{-1}\biggl[ \frac{(\xi_1\xi_2 - 1 )}{(\xi_1- \xi_2)} \biggr] \biggr\}_{\xi_2 = \gamma_i}^{\xi_2 = \Gamma_i} \, . </math>

Gravitational Potential due to a Circular Torus

<math>~\Phi_i(a,Z_0)</math>	<math>~=</math>	<math>~\frac{2^{5/2} G \rho_0 a^{2}}{3} \int\limits_{\xi_1 = \lambda_i}^{\xi_1 = \Lambda_i} \frac{(\xi_1+1)^{1/2}K(\mu) d\xi_1}{(\xi_1^2 - 1)^2 [ (\xi_1^2 - 1)^{1/2}+\xi_1 ]^{1/2} } \biggr[ \frac{\sin \theta(5\xi_1^2 - 4\xi_1 \cos \theta - 1)}{(\xi_1+1)^{1/2} (\xi_1 - \cos \theta)^{3/2}} </math>
		<math>~ - 4\xi_1 E\biggl( \frac{\pi-\theta}{2} \, , \sqrt{\frac{2}{\xi_1 + 1}} \biggr) + (\xi_1-1) F\biggl( \frac{\pi-\theta}{2} \, , \sqrt{\frac{2}{\xi_1 + 1}} \biggr) \biggr]_{\theta = \cos^{-1}(\gamma_i)}^{\theta = \cos^{-1}(\Gamma_i)} \, . </math>

Integration Limits

We define the following terms that are functions only of the four principal model parameters, <math>~(a, Z_0, \varpi_t, r_t)</math>, and therefore can be treated as constants while carrying out the pair of nested integrals that determine <math>~q_0</math>.

Zone I:

Figure 4: Zone I
Definition	Schematic Example
<math>~Z_0 > r_t</math> for any <math>~a</math>

In an accompanying discussion, we have derived the following integration limits; numerical values are given for the specific case, <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{3}{4}, \tfrac{3}{4}, \tfrac{1}{4})</math>:

<math>~\Lambda_1 = \xi_1\|_\mathrm{max} </math>	<math>~=</math>	<math>~\biggl[1-\biggl( \frac{a}{\varpi_t-\beta_+} \biggr)^2 \biggr]^{-1/2} \approx 1.1927843</math>
<math>~\lambda_1 = \xi_1\|_\mathrm{min} </math>	<math>~=</math>	<math>~\biggl[1-\biggl( \frac{a}{\varpi_t-\beta_-} \biggr)^2 \biggr]^{-1/2} \approx 1.0449467</math>

where,

<math>~\kappa</math>	<math>~\equiv</math>	<math>~ Z_0^2 + a^2 - (\varpi_t^2 - r_t^2) </math>	<math>\rightarrow</math>	<math>~ \frac{5^2}{2^4\cdot 3^2} \approx 0.17361111 </math>
<math>~C</math>	<math>~\equiv</math>	<math>~1 + \biggl( \frac{2Z_0}{\kappa}\biggr)^2 ( \varpi_t^2 - r_t^2) </math>	<math>\rightarrow</math>	<math>~\frac{17 \cdot 1409}{5^4} \approx 38.3248 </math>
<math>~\beta_\pm</math>	<math>~\equiv</math>	<math>~ - \frac{\kappa}{2} \biggl[ \frac{\varpi_t \mp r_t \sqrt{C}}{(\varpi_t + r_t)(\varpi_t - r_t)} \biggr] </math>	<math>\rightarrow</math>	<math>~ -~\frac{5^2}{2^6\cdot 3}\biggl[ 1\mp \sqrt{ \frac{17\cdot 1409}{3^2\cdot 5^4}} \biggr] </math>

Notice that we have specified these integration limits such that, in going from the lower limit <math>~(\lambda_1)</math> to the upper limit <math>~(\Lambda_1)</math>, the value of <math>~\xi_1</math> monotonically increases.

Also,

<math>~\Gamma_1 = \xi_2\biggr\|_+</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_+} </math>
<math>~\gamma_1 = \xi_2\biggr\|_-</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_-} </math>

where, in addition to the quantities defined above,

<math>~\biggl(\frac{\varpi_i}{a}\biggr)_\pm</math>	<math>~\equiv</math>	<math>~\frac{\kappa}{2a^2}\cdot \frac{\mathrm{B}}{\mathrm{A}} \biggl[1 \pm \sqrt{1-\frac{AC}{B^2}} \biggr] </math>
<math>~\mathrm{A}</math>	<math>~\equiv</math>	<math>~\biggl(\frac{Z_0}{a}\biggr)^2 + \biggl[\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}}\biggr]^2 </math>
<math>~\mathrm{B}</math>	<math>~\equiv</math>	<math>~\biggl(\frac{2\varpi_t Z_0^2}{a\kappa}\biggr) - \biggl[\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}}\biggr] </math>

Here, our desire also is to specify the integration limits such that <math>~\xi_2</math> monotonically increases in going from the lower limit <math>~(\gamma_1)</math> to the upper limit <math>~(\Gamma_1)</math>. In order to check to see if this is the case, let's test the limiting values of <math>~\xi_2</math> when we are considering a radial-coordinate value roughly midway between its limits, say, when <math>~\xi_1 = 1.1</math>. For this specific case, we find,

<math>~\frac{\varpi_t}{a} - \frac{\xi_1}{(\xi_1^2-1)^{1/2}} = - 0.150397 \, ;</math>

<math>~\biggl(\frac{\varpi_i}{a}\biggr)_\pm = 2.263098\biggl[1 \pm \sqrt{1-0.898157} \biggr] \, ;</math>

<math>~\Rightarrow ~~~ \biggl(\frac{\varpi_i}{a}\biggr)_+ = 2.985318 \, ;</math>

<math>~\Rightarrow ~~~ \biggl(\frac{\varpi_i}{a}\biggr)_- = 1.540878 \, ;</math>

<math>~\Rightarrow ~~~ \xi_2\biggr|_+ = 0.946496 \, ;</math>

<math>~\Rightarrow ~~~ \xi_2\biggr|_- = 0.802600 \, .</math>

Hence, our ordering of the limits appears to be the one desired.

Zone II:

Figure 5: Zone II

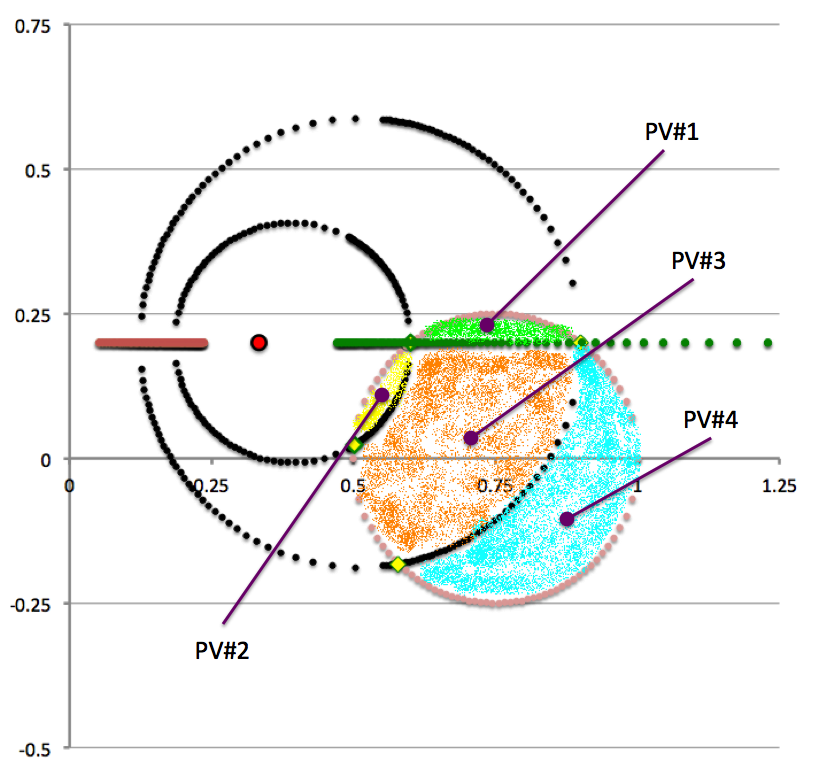
Definition

Schematic Example

Quantitative Example: Partial Volumes Identified

and

In an accompanying discussion, we have derived the following integration limits; example numerical values of various parameters are provided for the specific case where, <math>~(a, Z_0, \varpi_t, r_t) = (\tfrac{1}{3}, \tfrac{1}{5}, \tfrac{3}{4}, \tfrac{1}{4})</math>. Note that,

<math>~\kappa</math>	<math>~=</math>	<math>~- \frac{157}{2\cdot 3^2\cdot 5^2} \approx -0.34889 \, ;</math>
<math>~C</math>	<math>~=</math>	<math>~\frac{40849}{(157)^2} \approx 1.65723 \, ;</math>
<math>~\beta_+</math>	<math>~=</math>	<math>~\frac{1}{2^3\cdot 3^2\cdot 5^2} \biggl[3\cdot 157 - \sqrt{40849} \biggr] \approx 0.14938 \, ;</math>
<math>~\beta_-</math>	<math>~=</math>	<math>~\frac{1}{2^3\cdot 3^2\cdot 5^2} \biggl[3\cdot 157 + \sqrt{40849} \biggr] \approx 0.37395 \, .</math>

Partial Volume #1

This is the green cropped-top sub-volume identified as Partial Volume #1 (PV#1) in the right-hand panel of Figure 5, and discussed in detail elsewhere.

<math>~\Lambda_1 </math>	<math>~=</math>	<math>~\frac{[\varpi_t - \sqrt{r_t^2 - Z_0^2}]^2 + a^2}{[\varpi_t - \sqrt{r_t^2 - Z_0^2}]^2-a^2} ~\rightarrow~\frac{53}{2^2\cdot 7} \approx 1.89286</math>
<math>~\lambda_1 </math>	<math>~=</math>	<math>~\frac{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2 + a^2}{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2-a^2} ~\rightarrow~ \frac{829}{17\cdot 37} \approx 1.21797</math>

<math>~\Gamma_1 = \xi_2\biggr\|_+</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_+} </math>
<math>~\gamma_1 </math>	<math>~=</math>	<math>~1</math>

Partial Volume #2

This is the sub-volume that is painted yellow and identified as Partial Volume #2 (PV#2) in the right-hand panel of Figure 5.

<math>~\Lambda_2 </math>	<math>~=</math>	<math>~\frac{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2 + a^2}{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2-a^2}</math>
<math>~\lambda_2 = \xi_1\|_\mathrm{max}</math>	<math>~=</math>	<math>~\biggl[1-\biggl( \frac{a}{\varpi_t-\beta_+} \biggr)^2 \biggr]^{-1/2}</math>

<math>~\Gamma_2 = \xi_2\biggr\|_+</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_+} </math>
<math>~\gamma_2 = \xi_2\biggr\|_-</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_-} </math>

Partial Volume #3

This is the sub-volume that is painted orange and identified as Partial Volume #3 (PV#3) in the right-hand panel of Figure 5.

<math>~\Lambda_3 </math>	<math>~=</math>	<math>~\frac{[\varpi_t - \sqrt{r_t^2 - Z_0^2}]^2 + a^2}{[\varpi_t - \sqrt{r_t^2 - Z_0^2}]^2-a^2}</math>
<math>~\lambda_3 </math>	<math>~=</math>	<math>~\frac{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2 + a^2}{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2-a^2}</math>

<math>~\Gamma_3 </math>	<math>~=</math>	<math>~ 1 </math>
<math>~\gamma_3 = \xi_2\biggr\|_-</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_-} </math>

Partial Volume #4

This is the sub-volume that is painted light-blue and identified as Partial Volume #4 (PV#4) in the right-hand panel of Figure 5.

<math>~\Lambda_4 = \xi_1\|_\mathrm{min}</math>	<math>~=</math>	<math>~\biggl[1-\biggl( \frac{a}{\varpi_t-\beta_-} \biggr)^2 \biggr]^{-1/2}</math>
<math>~\lambda_4 </math>	<math>~=</math>	<math>~\frac{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2 + a^2}{[\varpi_t + \sqrt{r_t^2 - Z_0^2}]^2-a^2}</math>

<math>~\Gamma_4 = \xi_2\biggr\|_+</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_+} </math>
<math>~\gamma_4 = \xi_2\biggr\|_-</math>	<math>~=</math>	<math>~ \xi_1 - \frac{ (\xi_1^2-1)^{1/2}}{(\varpi_i/a)_-} </math>

Zone III