User:Tohline/H BookTiledMenu
Tiled Menu

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Context
| Principal Governing Equations (PGEs) |
Continuity | Euler | 1st Law of Thermodynamics |
Poisson |
|---|
| Equation of State (EOS) |
Total Pressure |
|---|
Spherically Symmetric Configurations
| One-Dimensional PGEs |
|---|
Equilibrium Structures
| Hydrostatic Balance Equation |
Solution Strategies |
|---|
| Isothermal Sphere |
via Direct Numerical Integration |
|---|
| Isolated Polytropes |
Known Analytic Solutions |
via Direct Numerical Integration |
via Self-Consistent Field (SCF) Technique |
|---|
| Zero-Temperature White Dwarf |
Chandrasekhar Limiting Mass |
|---|
| Pressure-Truncated Configurations |
Bonnor-Ebert (Isothermal) Spheres |
Polytropes | Equilibrium Sequence Turning-Points |
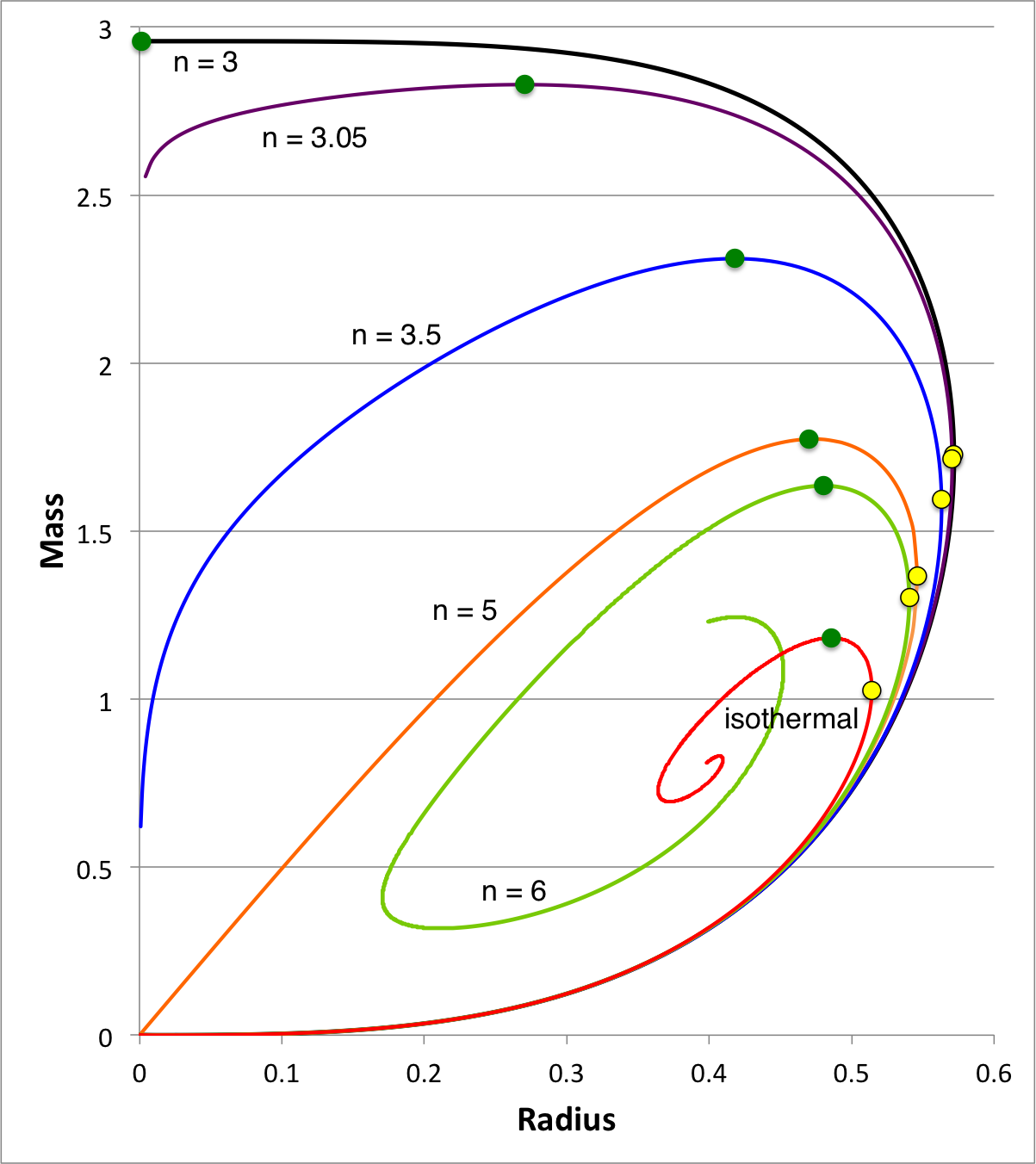
|
|---|
Stability Analysis
| Radial Pulsation Equation |
Example Derivations & Statement of Eigenvalue Problem |
Relationship to Sound Waves |
|---|
| Uniform-Density Configurations |
Sterne's Analytic Sol'n of Eigenvalue Problem |
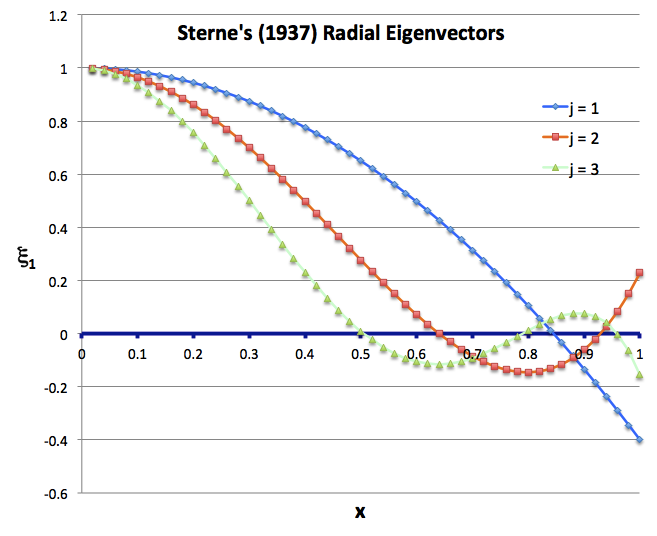
|
|---|
| Pressure-Truncated Isothermal Spheres |
|
via Direct Numerical Integration |
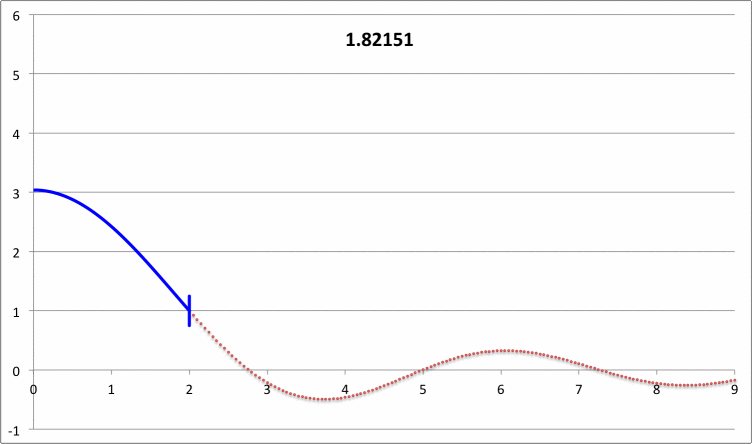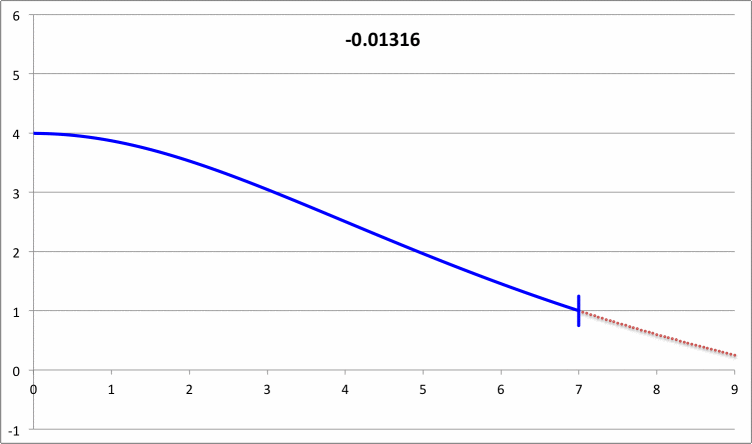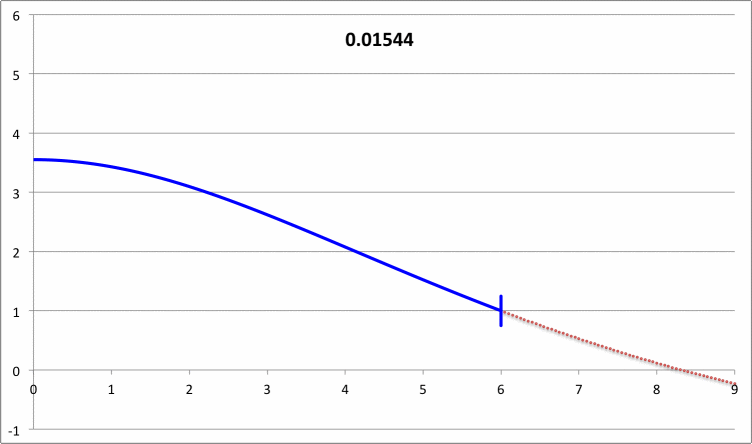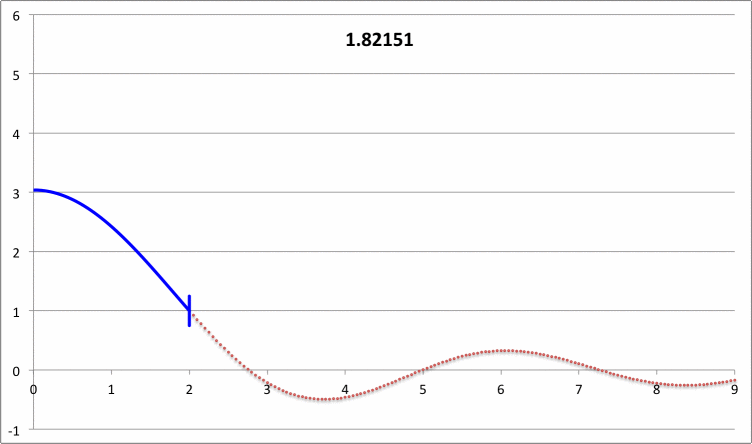
|
Yabushita's Analytic Sol'n for Marginally Unstable Configurations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polytropes |
|
Isolated n = 3 Polytrope |
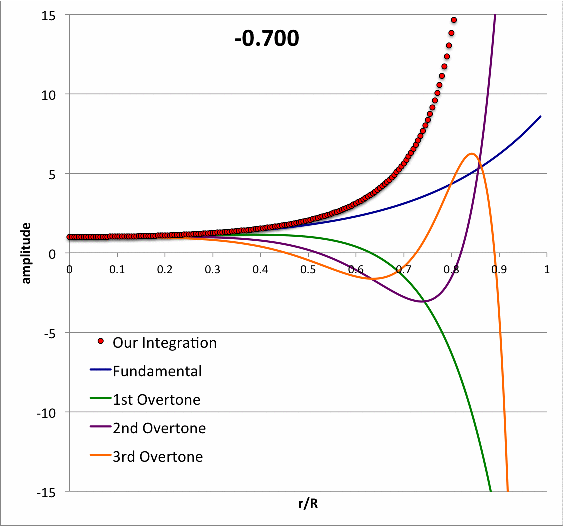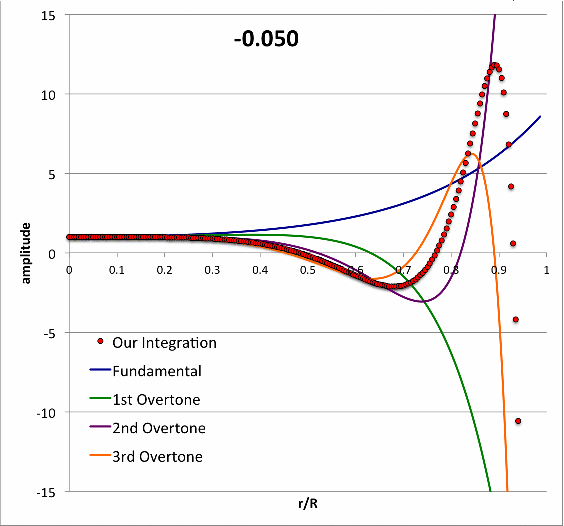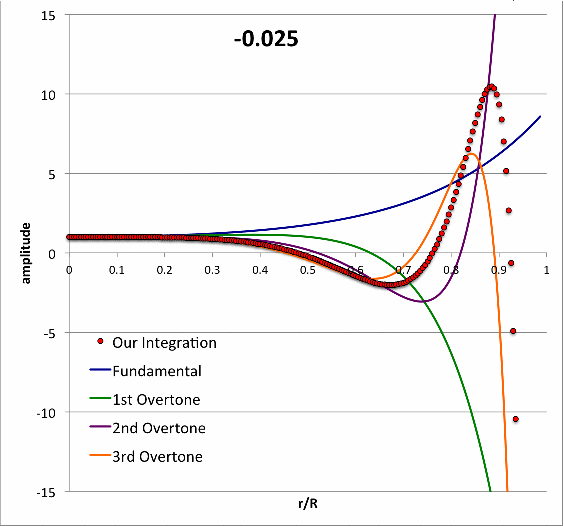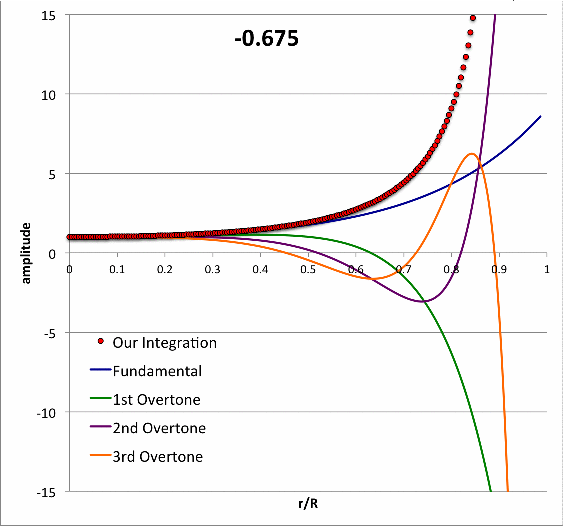
|
Pressure-Truncated Configurations |
Our Analytic Sol'n for Marginally Unstable Configurations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Nonlinear Dynamical Evolution
| Free-Fall Collapse |
|---|
| Collapse of Isothermal Spheres |
via Direct Numerical Integration |
Self-Similar Solution |
|---|
| Collapse of an Isolated n = 3 Polytrope |
|---|
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |


