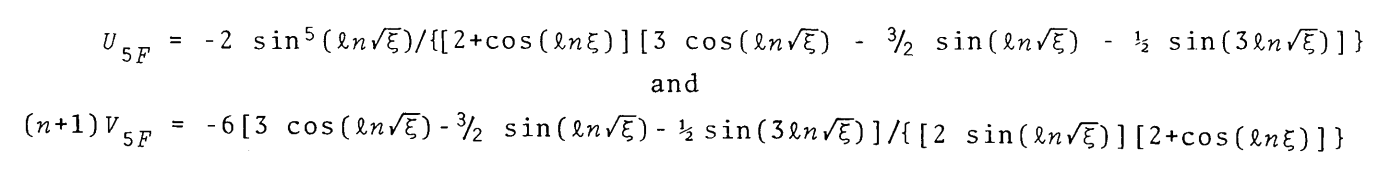User:Tohline/SSC/Structure/BiPolytropes/MurphyUVplane

UV Plane Functions as Analyzed by Murphy (1983)

This chapter supports and expands upon an accompanying discussion of the construction of a bipolytrope in which the core has an <math>~n_c=1</math> polytropic index and the envelope has an <math>~n_e=5</math> polytropic index. This system is particularly interesting because the entire structure can be described by closed-form, analytic expressions. Here we provide an in-depth analysis of the work published by J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175) in which the derivation of this particular bipolytropic configuration was first attempted. As can be seen from the following list of "key references," however, this publication was only one of a series of interrelated works by Murphy. We will henceforth refer to this <math>~(n_c, n_e) = (1, 5)</math> system as "Murphy's bipolytrope."

Key References

• S. Srivastava (1968, ApJ, 136, 680) A New Solution of the Lane-Emden Equation of Index n = 5
• H. A. Buchdahl (1978, Australian Journal of Physics, 31, 115): Remark on the Polytrope of Index 5 — the result of this work by Buchdahl has been highlighted inside our discussion of bipolytropes with <math>~(n_c, n_e) = (5, 1)</math>.
• J. O. Murphy (1980a, Proc. Astr. Soc. of Australia, 4, 37): A Finite Radius Solution for the Polytrope Index 5
• J. O. Murphy (1980b, Proc. Astr. Soc. of Australia, 4, 41): On the F-Type and M-Type Solutions of the Lane-Emden Equation
• J. O. Murphy (1981, Proc. Astr. Soc. of Australia, 4, 205): Physical Characteristics of a Polytrope Index 5 with Finite Radius
• J. O. Murphy (1982, Proc. Astr. Soc. of Australia, 4, 376): A Sequence of E-Type Composite Analytical Solutions of the Lane-Emden Equation
• J. O. Murphy (1983, Australian Journal of Physics, 36, 453): Structure of a Sequence of Two-Zone Polytropic Stellar Models with Indices 0 and 1
• J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175): Composite and Analytical Solutions of the Lane-Emden Equation with Polytropic Indices n = 1 and n = 5
• J. O. Murphy & R. Fiedler (1985a, Proc. Astr. Soc. of Australia, 6, 219): Physical Structure of a Sequence of Two-Zone Polytropic Stellar Models
• J. O. Murphy & R. Fiedler (1985b, Proc. Astr. Soc. of Australia, 6, 222): Radial Pulsations and Vibrational Stability of a Sequence of Two-Zone Polytropic Stellar Models

Relevant Lane-Emden Functions

As is detailed in our accompanying discussion, the Lane-Emden function governing the structure of the core of Murphy's bipolytrope is,

<math> \theta(\xi) = \frac{\sin\xi}{\xi} \, , </math>

and the first derivative of this function with respect to the dimensionless radial coordinate, <math>~\xi</math>, is,

<math> \frac{d\theta}{d\xi} = -\frac{1}{\xi^{2}} (\sin\xi - \xi\cos\xi) \, . </math>

Also as is detailed in our accompanying discussion, the Lane-Emden function governing the structure of the envelope of Murphy's bipolytrope is,

<math>~\phi(\eta)</math>	<math>~=</math>	<math>~\frac{B^{-1}\sin[\ln(A\eta)^{1/2})]}{\eta^{1/2}\{3-2\sin^2[\ln(A\eta)^{1/2}]\}^{1/2}} </math>
	<math>~=</math>	<math>~\frac{B^{-1}\sin\Delta}{\eta^{1/2}(3-2\sin^2\Delta)^{1/2}} \, ,</math>

and the first derivative of this function is,

<math>~\frac{d\phi}{d\eta}</math>

<math>~=</math>

<math>~- \frac{B^{-1}(3\sin\Delta - 2\sin^3\Delta -3\cos\Delta) }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} \, , </math>

where we have adopted the shorthand notation,

<math>~\Delta \equiv \ln(A\eta)^{1/2} \, .</math>

Chandrasekhar's U and V Functions

As presented by Murphy (1983), most of the development and analysis of this model was conducted within the framework of what is commonly referred to in the astrophysics community as the "U-V" plane. Specifically in the context of the model's <math>~n=5</math> envelope, this pair of referenced functions are:

<math>~U_{5F} \equiv \eta \phi^5 \biggl(- \frac{d\phi}{d\eta}\biggr)^{-1}</math>	<math>~=</math>	<math>~ \frac{B^{-4}\eta \sin^5\Delta}{\eta^{5/2}\{3-2\sin^2\Delta\}^{5/2}} \biggl[ \frac{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}}{3\sin\Delta - 2\sin^3\Delta -3\cos\Delta } \biggr] </math>
	<math>~=</math>	<math>~ \frac{2B^{-4}\sin^5\Delta}{[3-2\sin^2\Delta][3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ]} </math>
	<math>~=</math>	<math>~ \frac{-2B^{-4}\sin^5\Delta}{[2+\cos(2\Delta)][3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ]} \, ; </math>
<math>~V_{5F} \equiv \frac{\eta}{ \phi} \biggl(- \frac{d\phi}{d\eta}\biggr)</math>	<math>~=</math>	<math>~\frac{\eta^{3/2}\{3-2\sin^2\Delta\}^{1/2}} {\sin\Delta} \frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} </math>
	<math>~=</math>	<math>~\frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\sin\Delta (3-2\sin^2\Delta)} </math>
	<math>~=</math>	<math>~\frac{-[3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ] }{2\sin\Delta [2+\cos(2\Delta)]} \, . </math>

After recognizing that <math>~\cos(2\Delta) = \cos(2\ln\eta^{1/2}) = \cos(\ln\eta)\, ,</math> we see that these expressions for the functions, <math>~U_{5F}</math> and <math>~V_{5F}</math>, match the expressions used by Murphy (1983) and reproduced (slightly edited) here as an image, for ease of comparison:

<\td>

Related Discussions

• Bipolytrope with n_c = 1 and n_e=5
• Polytropes emdeded in an external medium
• Constructing BiPolytropes

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation