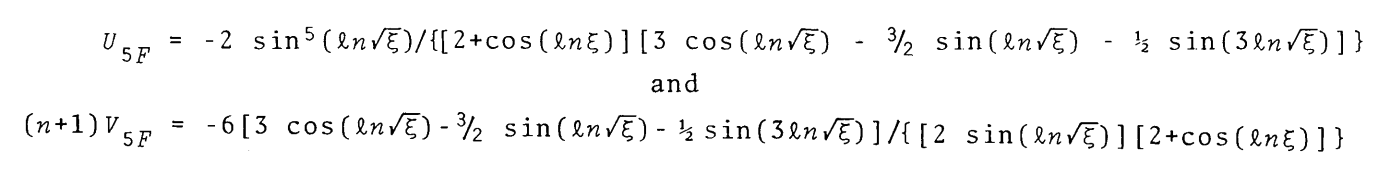Difference between revisions of "User:Tohline/SSC/Structure/BiPolytropes/MurphyUVplane"
(Begin laying out text of this new chapter, borrowing from our more complete discussion of this bipolytrope's construction) |
(→Chandrasekhar's U and V Functions: Get rid of large "bordered table box" surrounding original text) |
||
| Line 87: | Line 87: | ||
==Chandrasekhar's U and V Functions== | ==Chandrasekhar's U and V Functions== | ||
As presented by [http://adsabs.harvard.edu/abs/1983PASAu...5..175M Murphy (1983)], most of the development and analysis of this model was conducted within the framework of what is commonly referred to in the astrophysics community as the "U-V" plane. Specifically in the context of the model's <math>~n=5</math> envelope, this pair of referenced functions are: | As presented by [http://adsabs.harvard.edu/abs/1983PASAu...5..175M Murphy (1983)], most of the development and analysis of this model was conducted within the framework of what is commonly referred to in the astrophysics community as the "U-V" plane. Specifically in the context of the model's <math>~n=5</math> envelope, this pair of referenced functions are: | ||
<div align="center"> | <div align="center"> | ||
| Line 187: | Line 177: | ||
After recognizing that <math>~\cos(2\Delta) = \cos(2\ln\eta^{1/2}) = \cos(\ln\eta)\, ,</math> we see that these expressions for the functions, <math>~U_{5F}</math> and <math>~V_{5F}</math>, match the expressions used by [http://adsabs.harvard.edu/abs/1983PASAu...5..175M Murphy (1983)] and reproduced (slightly edited) here as an image, for ease of comparison: | After recognizing that <math>~\cos(2\Delta) = \cos(2\ln\eta^{1/2}) = \cos(\ln\eta)\, ,</math> we see that these expressions for the functions, <math>~U_{5F}</math> and <math>~V_{5F}</math>, match the expressions used by [http://adsabs.harvard.edu/abs/1983PASAu...5..175M Murphy (1983)] and reproduced (slightly edited) here as an image, for ease of comparison: | ||
<table border=" | <table border="1" cellpadding="8" align="center"> | ||
<tr><td align="center"> | <tr><td align="center"> | ||
[[File:Murphy1983UVfunctions.png|center|700px|U_5F and V_5F Functions by Murphy (1983)]] | [[File:Murphy1983UVfunctions.png|center|700px|U_5F and V_5F Functions by Murphy (1983)]] | ||
=Related Discussions= | =Related Discussions= | ||
Revision as of 20:52, 1 May 2015
UV Plane Functions as Analyzed by Murphy (1983)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
This chapter supports and expands upon an accompanying discussion of the construction of a bipolytrope in which the core has an <math>~n_c=1</math> polytropic index and the envelope has an <math>~n_e=5</math> polytropic index. This system is particularly interesting because the entire structure can be described by closed-form, analytic expressions. Here we provide an in-depth analysis of the work published by J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175) in which the derivation of this particular bipolytropic configuration was first attempted. As can be seen from the following list of "key references," however, this publication was only one of a series of interrelated works by Murphy. We will henceforth refer to this <math>~(n_c, n_e) = (1, 5)</math> system as "Murphy's bipolytrope."
Key References
- S. Srivastava (1968, ApJ, 136, 680) A New Solution of the Lane-Emden Equation of Index n = 5
- H. A. Buchdahl (1978, Australian Journal of Physics, 31, 115): Remark on the Polytrope of Index 5 — the result of this work by Buchdahl has been highlighted inside our discussion of bipolytropes with <math>~(n_c, n_e) = (5, 1)</math>.
- J. O. Murphy (1980a, Proc. Astr. Soc. of Australia, 4, 37): A Finite Radius Solution for the Polytrope Index 5
- J. O. Murphy (1980b, Proc. Astr. Soc. of Australia, 4, 41): On the F-Type and M-Type Solutions of the Lane-Emden Equation
- J. O. Murphy (1981, Proc. Astr. Soc. of Australia, 4, 205): Physical Characteristics of a Polytrope Index 5 with Finite Radius
- J. O. Murphy (1982, Proc. Astr. Soc. of Australia, 4, 376): A Sequence of E-Type Composite Analytical Solutions of the Lane-Emden Equation
- J. O. Murphy (1983, Australian Journal of Physics, 36, 453): Structure of a Sequence of Two-Zone Polytropic Stellar Models with Indices 0 and 1
- J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175): Composite and Analytical Solutions of the Lane-Emden Equation with Polytropic Indices n = 1 and n = 5
- J. O. Murphy & R. Fiedler (1985a, Proc. Astr. Soc. of Australia, 6, 219): Physical Structure of a Sequence of Two-Zone Polytropic Stellar Models
- J. O. Murphy & R. Fiedler (1985b, Proc. Astr. Soc. of Australia, 6, 222): Radial Pulsations and Vibrational Stability of a Sequence of Two-Zone Polytropic Stellar Models
Relevant Lane-Emden Functions
As is detailed in our accompanying discussion, the Lane-Emden function governing the structure of the core of Murphy's bipolytrope is,
<math> \theta(\xi) = \frac{\sin\xi}{\xi} \, , </math>
and the first derivative of this function with respect to the dimensionless radial coordinate, <math>~\xi</math>, is,
<math> \frac{d\theta}{d\xi} = -\frac{1}{\xi^{2}} (\sin\xi - \xi\cos\xi) \, . </math>
Also as is detailed in our accompanying discussion, the Lane-Emden function governing the structure of the envelope of Murphy's bipolytrope is,
|
<math>~\phi(\eta)</math> |
<math>~=</math> |
<math>~\frac{B^{-1}\sin[\ln(A\eta)^{1/2})]}{\eta^{1/2}\{3-2\sin^2[\ln(A\eta)^{1/2}]\}^{1/2}} </math> |
|
|
<math>~=</math> |
<math>~\frac{B^{-1}\sin\Delta}{\eta^{1/2}(3-2\sin^2\Delta)^{1/2}} \, ,</math> |
and the first derivative of this function is,
|
<math>~\frac{d\phi}{d\eta}</math> |
<math>~=</math> |
<math>~- \frac{B^{-1}(3\sin\Delta - 2\sin^3\Delta -3\cos\Delta) }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} \, , </math> |
where we have adopted the shorthand notation,
<math>~\Delta \equiv \ln(A\eta)^{1/2} \, .</math>
Chandrasekhar's U and V Functions
As presented by Murphy (1983), most of the development and analysis of this model was conducted within the framework of what is commonly referred to in the astrophysics community as the "U-V" plane. Specifically in the context of the model's <math>~n=5</math> envelope, this pair of referenced functions are:
|
<math>~U_{5F} \equiv \eta \phi^5 \biggl(- \frac{d\phi}{d\eta}\biggr)^{-1}</math> |
<math>~=</math> |
<math>~ \frac{B^{-4}\eta \sin^5\Delta}{\eta^{5/2}\{3-2\sin^2\Delta\}^{5/2}} \biggl[ \frac{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}}{3\sin\Delta - 2\sin^3\Delta -3\cos\Delta } \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2B^{-4}\sin^5\Delta}{[3-2\sin^2\Delta][3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ]} </math> |
|
|
<math>~=</math> |
<math>~ \frac{-2B^{-4}\sin^5\Delta}{[2+\cos(2\Delta)][3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ]} \, ; </math> |
|
<math>~V_{5F} \equiv \frac{\eta}{ \phi} \biggl(- \frac{d\phi}{d\eta}\biggr)</math> |
<math>~=</math> |
<math>~\frac{\eta^{3/2}\{3-2\sin^2\Delta\}^{1/2}} {\sin\Delta} \frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} </math> |
|
|
<math>~=</math> |
<math>~\frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\sin\Delta (3-2\sin^2\Delta)} </math> |
|
|
<math>~=</math> |
<math>~\frac{-[3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ] }{2\sin\Delta [2+\cos(2\Delta)]} \, . </math> |
After recognizing that <math>~\cos(2\Delta) = \cos(2\ln\eta^{1/2}) = \cos(\ln\eta)\, ,</math> we see that these expressions for the functions, <math>~U_{5F}</math> and <math>~V_{5F}</math>, match the expressions used by Murphy (1983) and reproduced (slightly edited) here as an image, for ease of comparison:
Related Discussions
| ||||