User:Tohline/2DStructure/ToroidalCoordinateIntegrationLimits

Toroidal-Coordinate Integration Limits

In support of our accompanying discussion of the gravitational potential of a uniform-density circular torus, here we explain in detail what limits of integration must be specified in order to accurately determine the volume — and, hence also the total mass — of such a torus using toroidal coordinates.

Preamble

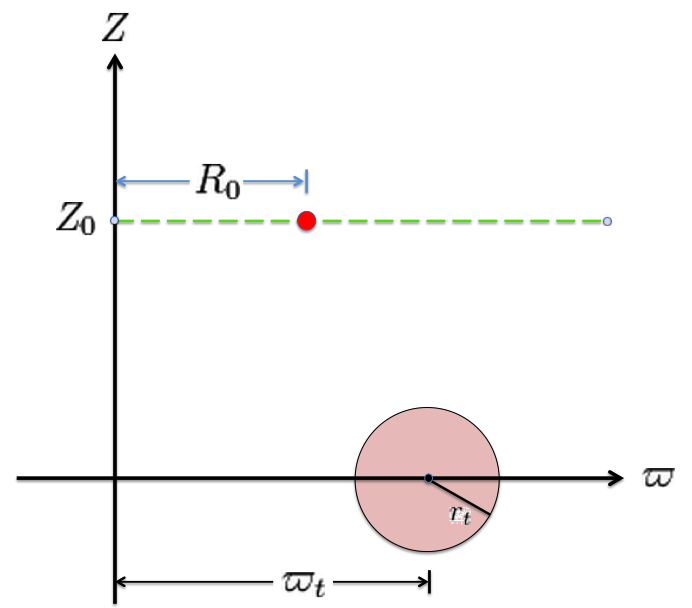
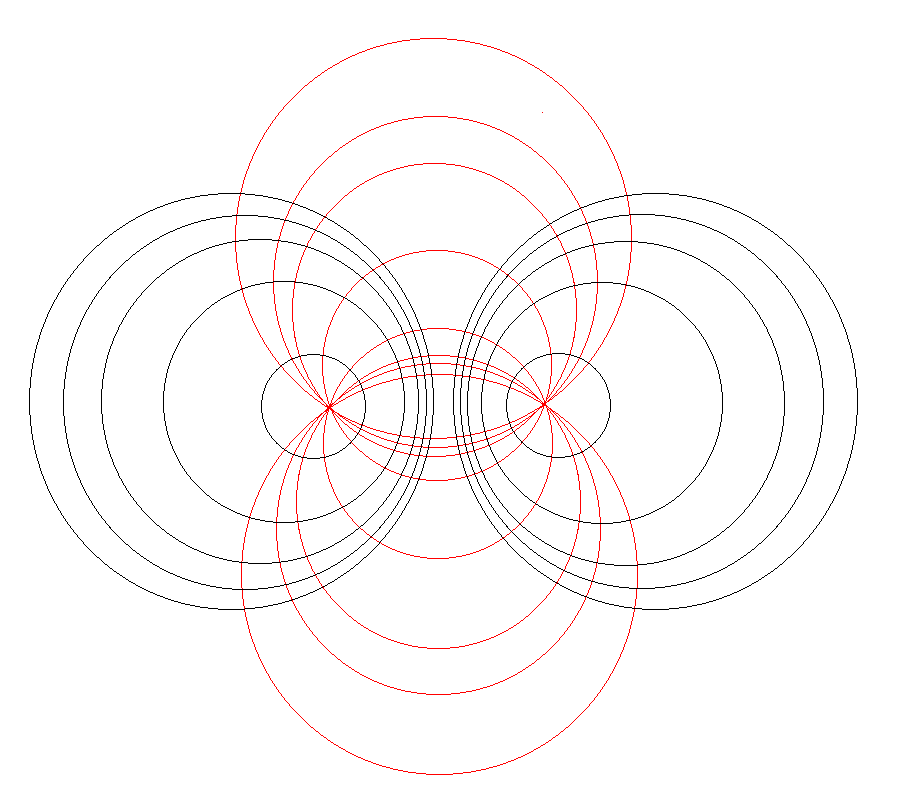
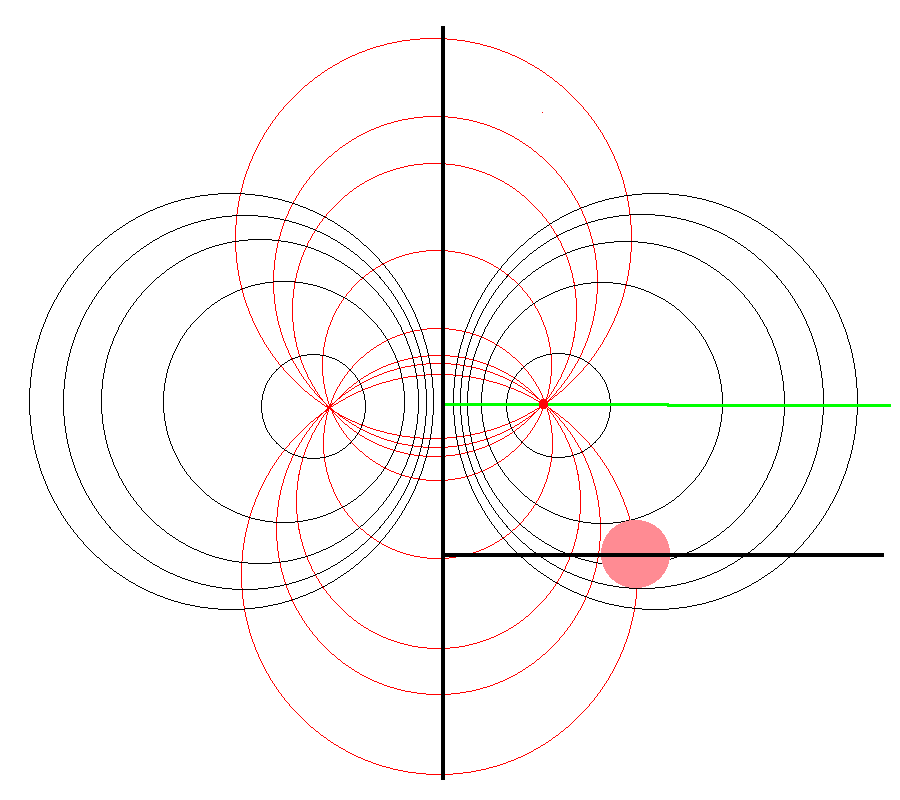
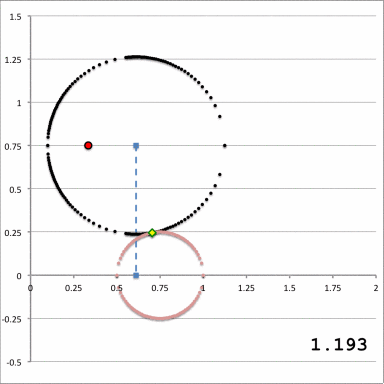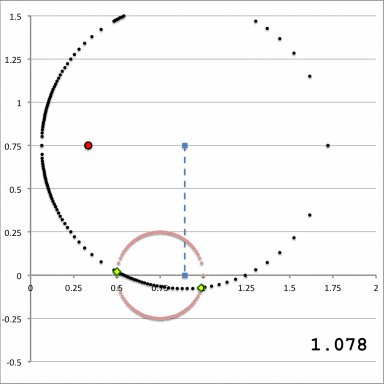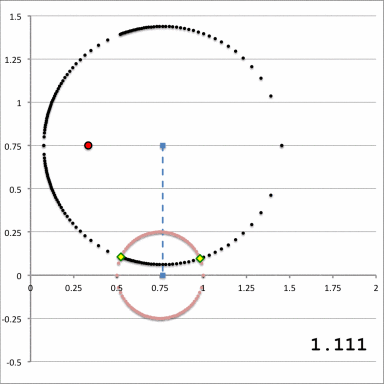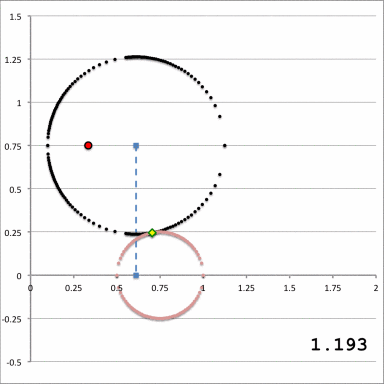
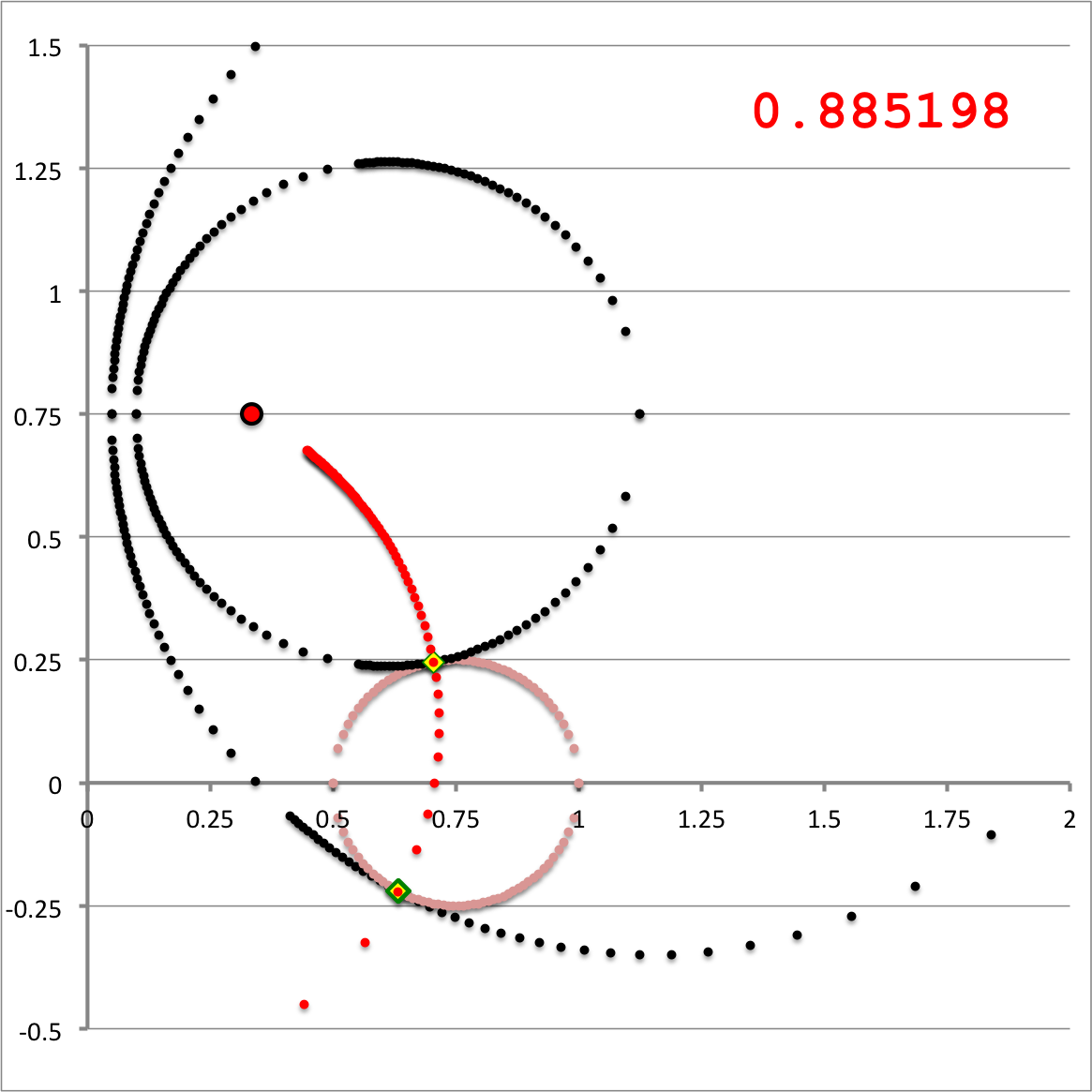
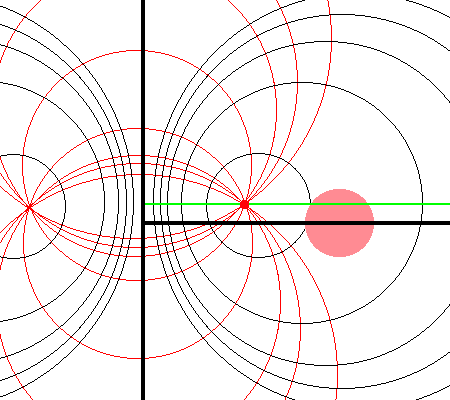
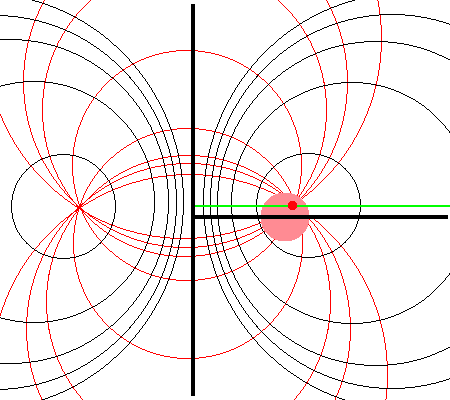
Referencing the illustration displayed in the left-hand panel of Figure 1, our goal is to determine the gravitational potential at any cylindrical-coordinate location <math>~(R_0, Z_0)</math> due to a uniform-density circular torus whose major radius is <math>~\varpi_t</math> and whose minor, cross-sectional radius is <math>~r_t</math>. Here we explain how a toroidal coordinate system <math>~(\xi_1, \xi_2)</math> — as defined, for example, by MF53 and as illustrated schematically in the right-hand panel of Figure 1 — can be used to reduce the geometric complexity of this problem. In particular, we show how, when using an appropriately aligned toroidal coordinate system, the three-dimensional, weighted integral over the mass distribution can be reduced to the sum of a small number (1 - 4) of one-dimensional integrals over the "radial" <math>~(\xi_1)</math> coordinate.

Figure 1:    Meridional slice through …
(Pink) Circular Torus	Toroidal Coordinate System (schematic) (see also Wikipedia's Apollonian Circles)
The pink circle represents the meridional cross-section through an axisymmetric, circular torus that lies in the equatorial plane of a cylindrical <math>~(\varpi, Z)</math>, coordinate system. The torus has a major axis of length, <math>~\varpi_t</math>, and a minor, cross-sectional radius of length, <math>~r_t</math>. The red circular dot identifies the cylindrical-coordinate location, <math>~(R_0, Z_0)</math>, at which the gravitational potential is to be evaluated.	As is explained more fully in Wikipedia's discussion of toroidal coordinates, rotating this two-dimensional bipolar coordinate system about the vertical axis produces a three-dimensional toroidal coordinate system. Black circles centered on the horizontal axis become circular tori — each identifying an axisymmetric, <math>\xi_1 =</math> constant surface; whereas, red circles centered on the vertical axis become spheres — each identifying an axisymmetric, <math>\xi_2 =</math> constant surface.

Quantitative Illustration of Employed Toroidal Coordinate System

Schematic Zones
Zone I <math>~Z_0 > r_t</math> for any <math>~a</math>	Zone II <math>~r_t > Z_0 > 0</math> and <math>~a < \varpi_t - \sqrt{r_t^2 - Z_0^2}</math>	Zone III <math>~r_t > Z_0 > 0</math> and <math>~\varpi_t - \sqrt{r_t^2 - Z_0^2} < a < \varpi_t + \sqrt{r_t^2 - Z_0^2}</math>

<math>~\frac{V_i}{V_\mathrm{torus}}</math> <math>~=</math> <math>~\frac{a^3}{2\pi \varpi_t r_t^2} \int\limits_{\xi_1 = \lambda_i}^{\xi_1 = \Lambda_i} d\xi_1 \biggl\{ \frac{(1-\xi_2^2)^{1/2} [ 4\xi_1^2 - 3\xi_1 \xi_2 - 1]}{(\xi_1^2-1)^2 (\xi_1 - \xi_2)^2} + \biggl[ \frac{(2\xi_1^2 + 1)}{(\xi_1^2-1)^{5/2}}\biggr] \cos^{-1}\biggl[ \frac{(\xi_1\xi_2 - 1 )}{(\xi_1- \xi_2)} \biggr] \biggr\}_{\xi_2 = \gamma_i}^{\xi_2 = \Gamma_i} \, . </math>

<math>~\Phi_i(a,Z_0)</math> <math>~=</math> <math>~\frac{2^{5/2} G \rho_0 a^{2}}{3} \int\limits_{\xi_1 = \lambda_i}^{\xi_1 = \Lambda_i} \frac{(\xi_1+1)^{1/2}K(\mu) d\xi_1}{(\xi_1^2 - 1)^2 [ (\xi_1^2 - 1)^{1/2}+\xi_1 ]^{1/2} } \biggr[ \frac{\sin \theta(5\xi_1^2 - 4\xi_1 \cos \theta - 1)}{(\xi_1+1)^{1/2} (\xi_1 - \cos \theta)^{3/2}} </math>     <math>~ - 4\xi_1 E\biggl( \frac{\pi-\theta}{2} \, , \sqrt{\frac{2}{\xi_1 + 1}} \biggr) + (\xi_1-1) F\biggl( \frac{\pi-\theta}{2} \, , \sqrt{\frac{2}{\xi_1 + 1}} \biggr) \biggr]_{\theta = \cos^{-1}(\gamma_i)}^{\theta = \cos^{-1}(\Gamma_i)} \, . </math>

See Also

• Wikipedia's discussion of Toroidal Coordinates

 

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation