Difference between revisions of "User:Tohline/2DStructure/ToroidalCoordinateIntegrationLimits"
(→Preamble: More preamble material, including general volume integral and general integral for the gravitational potential) |
|||
| Line 45: | Line 45: | ||
<math>~Z_0 > r_t</math><p></p>for any <math>~a</math></th> | <math>~Z_0 > r_t</math><p></p>for any <math>~a</math></th> | ||
<th align="center" colspan="1"><font size="+1">Zone II</font><p></p> | <th align="center" colspan="1"><font size="+1">Zone II</font><p></p> | ||
<math>~r_t > Z_0 > 0</math><p></p>and<p></p><math>~a < | <math>~r_t > Z_0 > 0</math><p></p>and<p></p><math>~a < \varpi_t - \sqrt{r_t^2 - Z_0^2}</math></th> | ||
<th align="center" colspan="1"><font size="+1">Zone III</font><p></p> | <th align="center" colspan="1"><font size="+1">Zone III</font><p></p> | ||
<math>~r_t > Z_0 > 0</math><p></p>and<p></p><math>~\varpi_t - \sqrt{r_t^2 - Z_0^2} < a < \ | <math>~r_t > Z_0 > 0</math><p></p>and<p></p><math>~\varpi_t - \sqrt{r_t^2 - Z_0^2} < a < \varpi_t + \sqrt{r_t^2 - Z_0^2}</math></th> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
Revision as of 02:53, 10 November 2015
Toroidal-Coordinate Integration Limits
In support of our accompanying discussion of the gravitational potential of a uniform-density circular torus, here we explain in detail what limits of integration must be specified in order to accurately determine the volume — and, hence also the total mass — of such a torus using toroidal coordinates.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Preamble
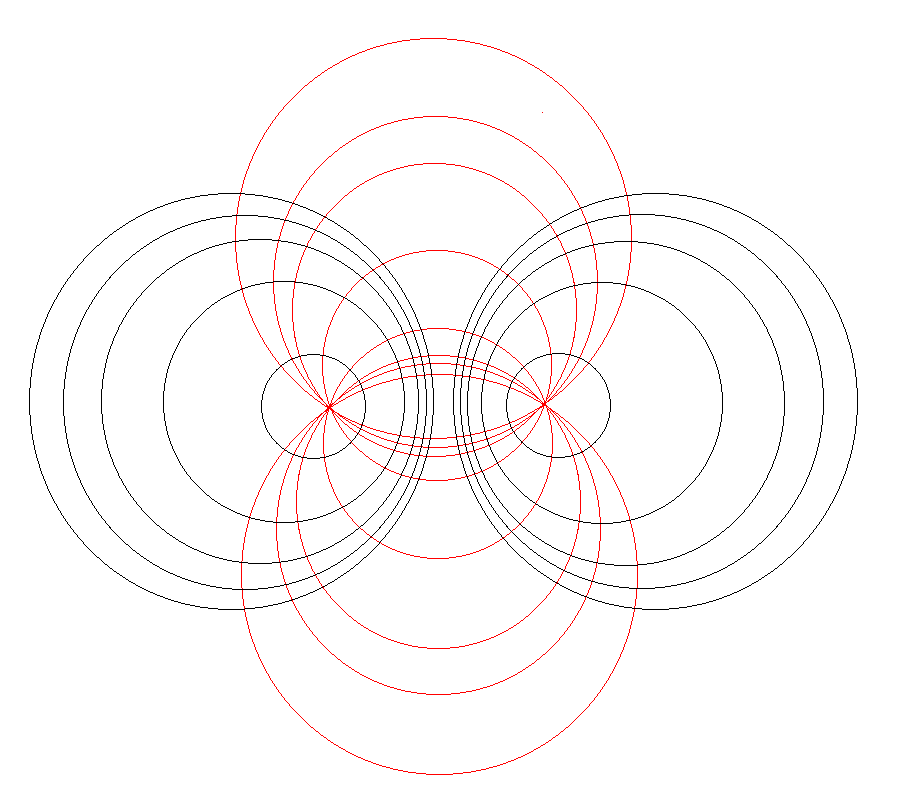
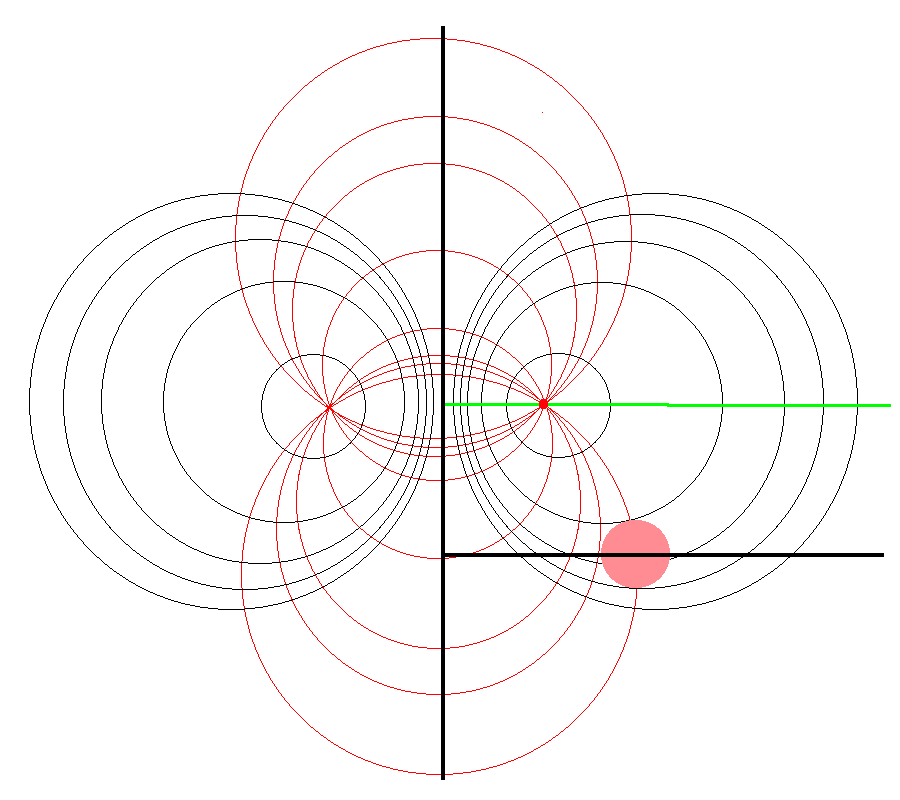
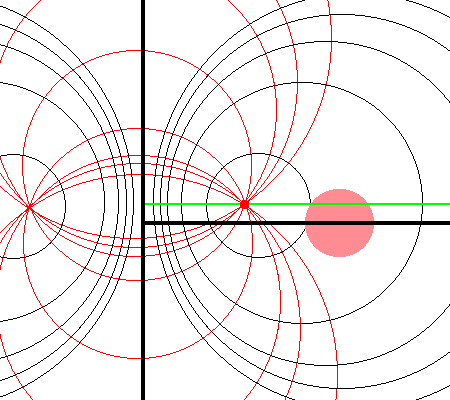
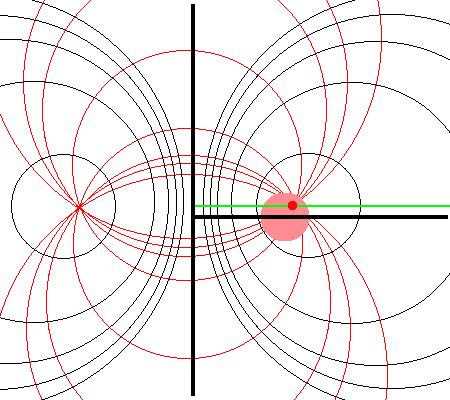
| Apollonian Circles (schematic) (see also Wikipedia's Apollonian Circles) | |
|---|---|
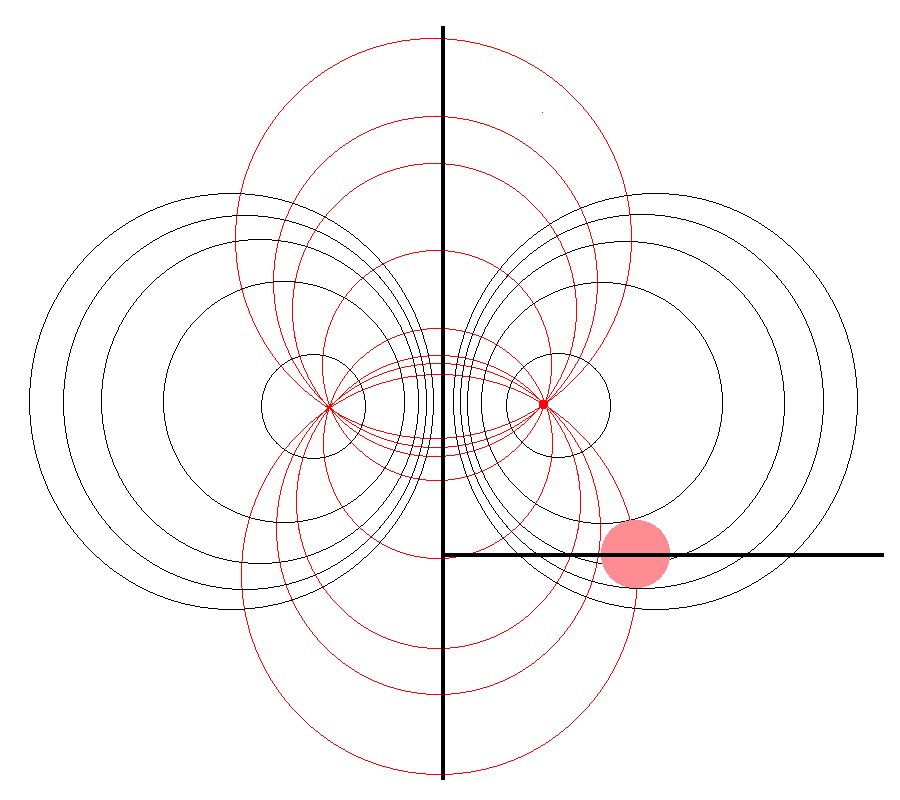
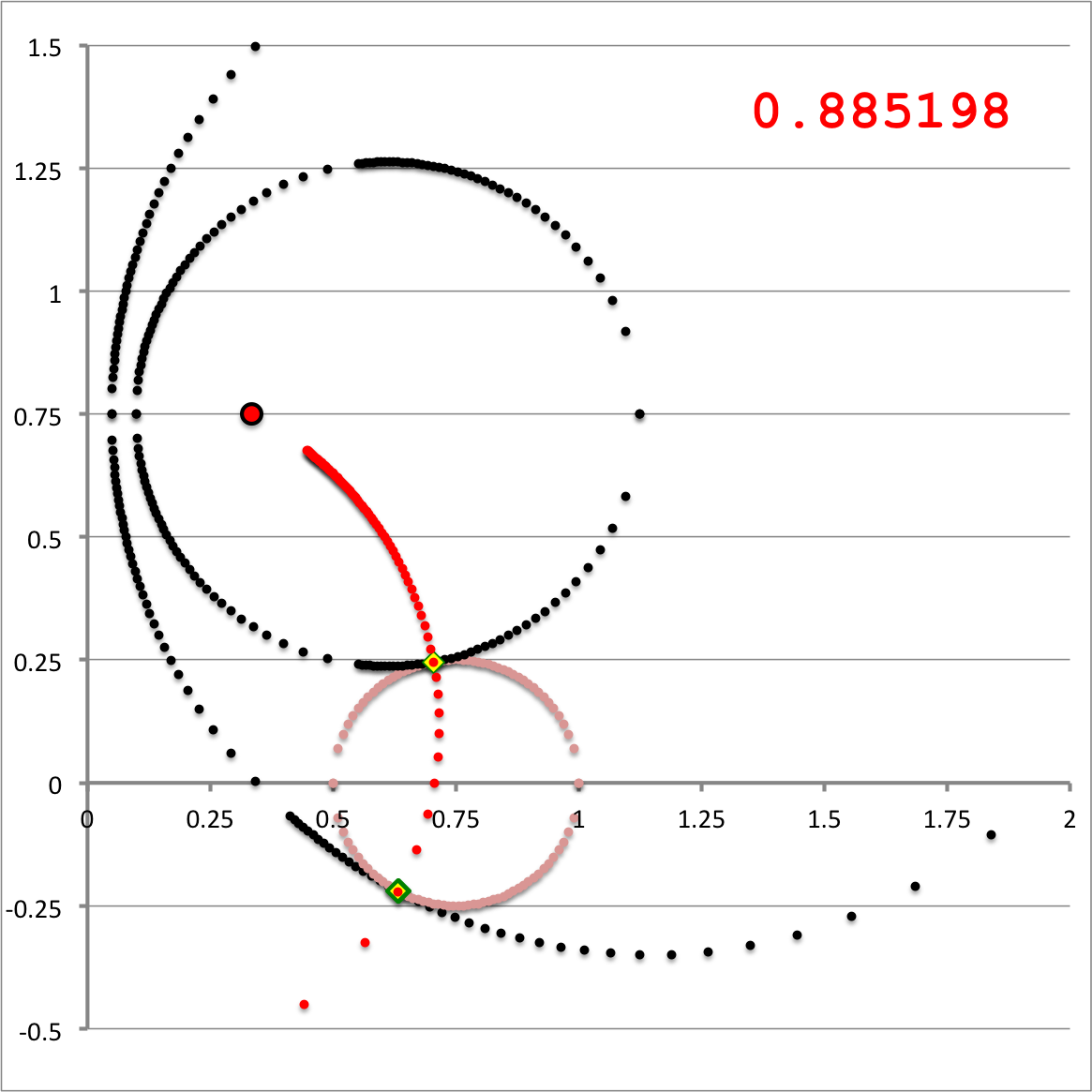
| Quantitative Illustration of Employed Toroidal Coordinate System | |
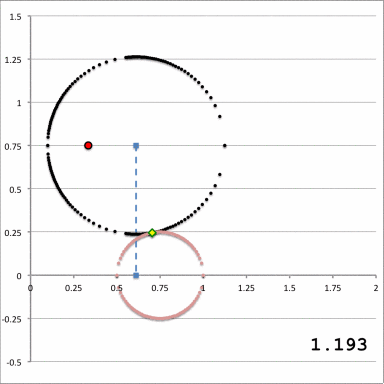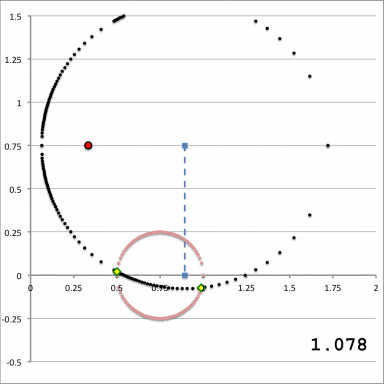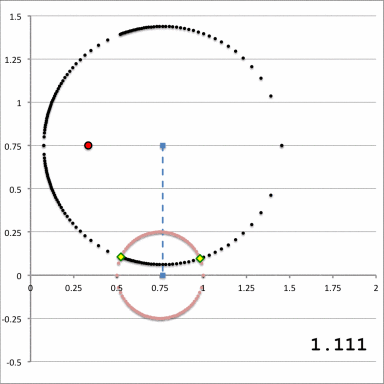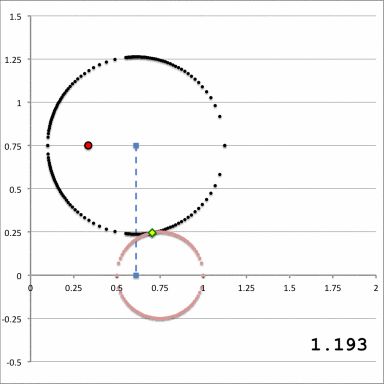
| Schematic Zones | ||
|---|---|---|
| Zone I <math>~Z_0 > r_t</math>for any <math>~a</math> | Zone II <math>~r_t > Z_0 > 0</math>and<math>~a < \varpi_t - \sqrt{r_t^2 - Z_0^2}</math> | Zone III <math>~r_t > Z_0 > 0</math>and<math>~\varpi_t - \sqrt{r_t^2 - Z_0^2} < a < \varpi_t + \sqrt{r_t^2 - Z_0^2}</math> |
|
|
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |