Toroidal-Coordinate Integration Limits
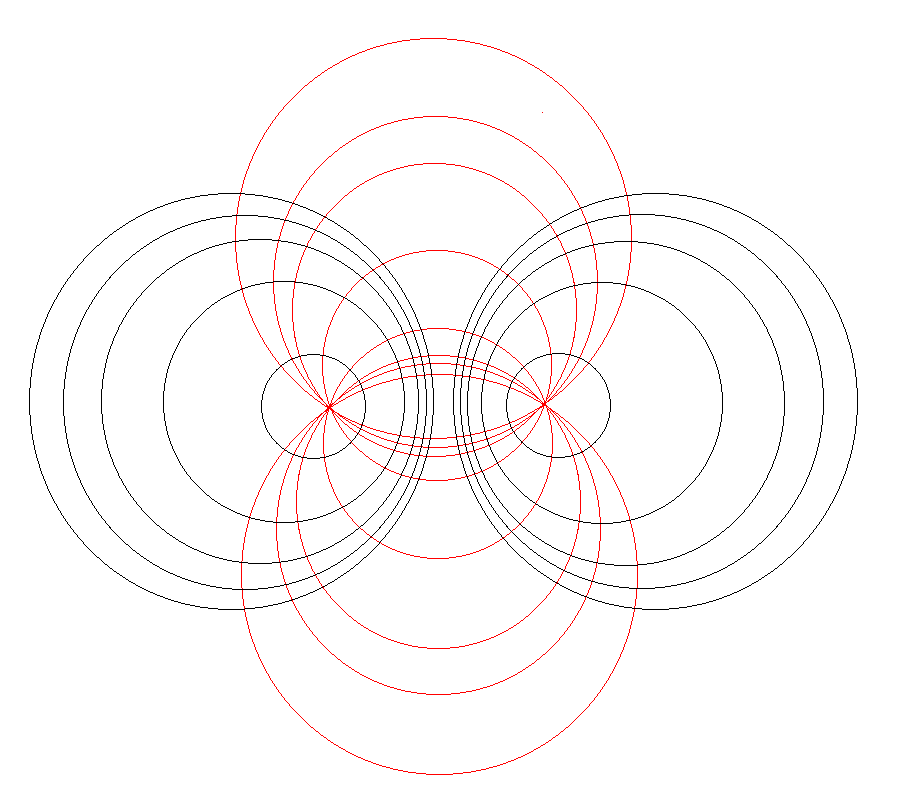
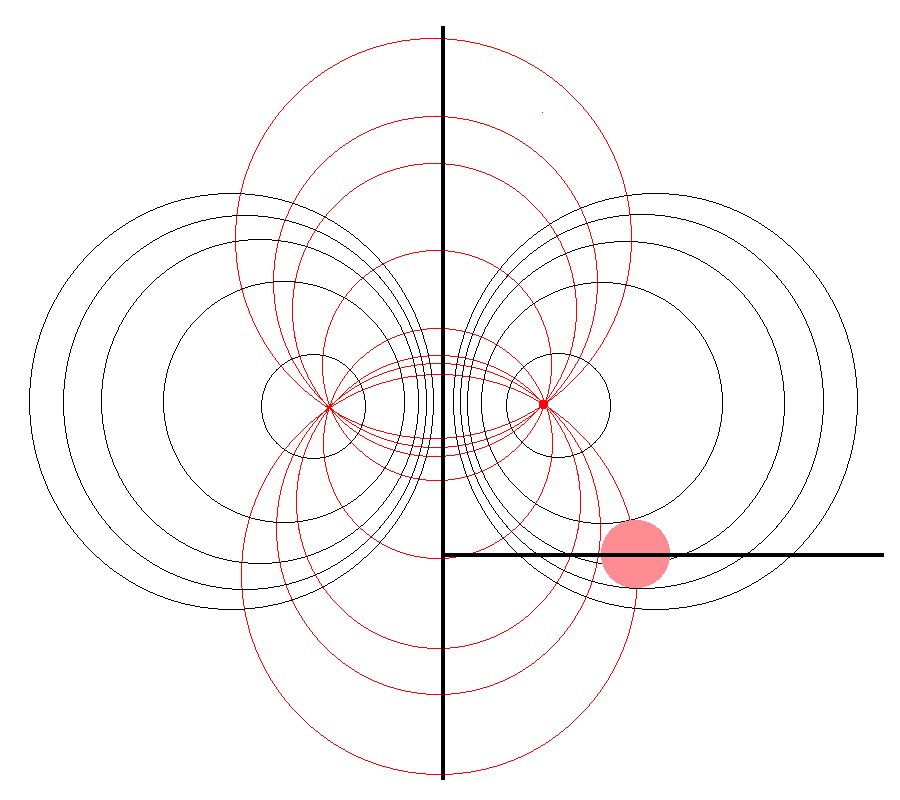
In support of our accompanying discussion of the gravitational potential of a uniform-density circular torus, here we explain in detail what limits of integration must be specified in order to accurately determine the volume — and, hence also the total mass — of such a torus using toroidal coordinates.
Preamble
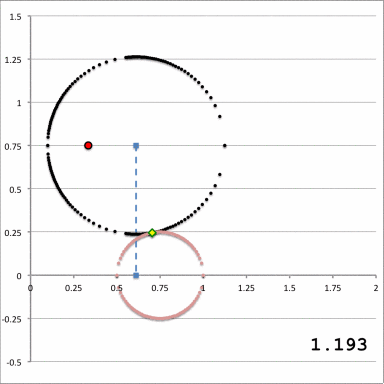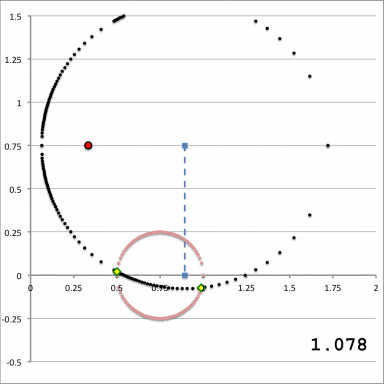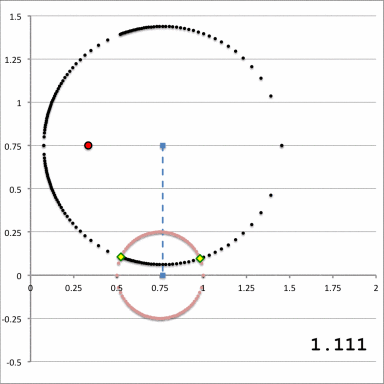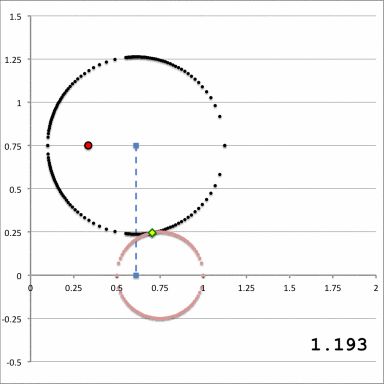
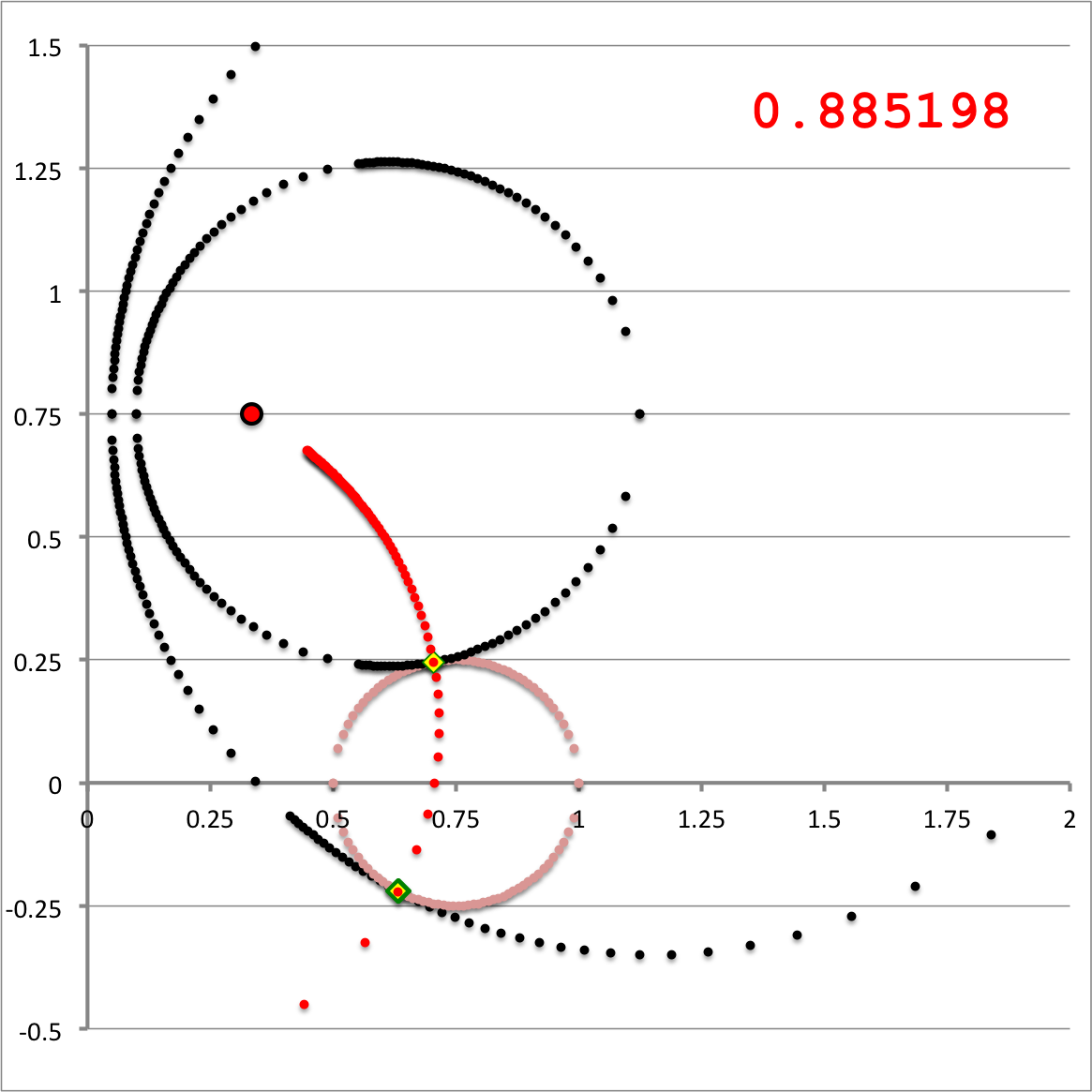
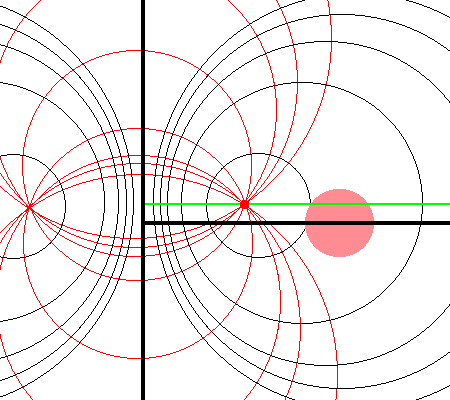
| Schematic Zones |
| Zone I
<math>~Z_0 > r_t</math>for any <math>~a</math> |
Zone II
<math>~r_t > Z_0 > 0</math>and<math>~a < (\varpi_t-r_t)</math> |
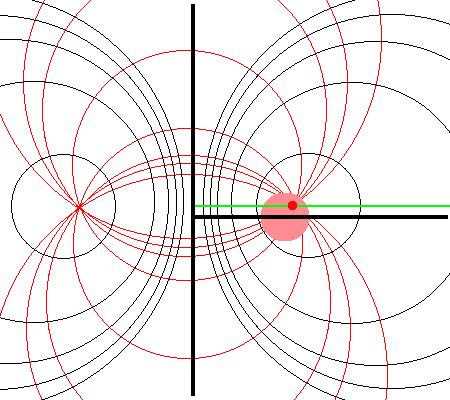
Zone III
<math>~r_t > Z_0 > 0</math>and<math>~\varpi_t - \sqrt{r_t^2 - Z_0^2} < a < \varpi+ + \sqrt{r_t^2 - Z_0^2}</math> |
|
|
|
|
|
<math>~\frac{V_i}{V_\mathrm{torus}}</math>
|
<math>~=</math>
|
<math>~\frac{a^3}{2\pi \varpi_t r_t^2} \int\limits_{\xi_1 = \lambda_i}^{\xi_1 = \Lambda_i} d\xi_1
\biggl\{
\frac{(1-\xi_2^2)^{1/2} [ 4\xi_1^2 - 3\xi_1 \xi_2 - 1]}{(\xi_1^2-1)^2 (\xi_1 - \xi_2)^2}
+ \biggl[ \frac{(2\xi_1^2 + 1)}{(\xi_1^2-1)^{5/2}}\biggr] \cos^{-1}\biggl[ \frac{(\xi_1\xi_2 - 1 )}{(\xi_1- \xi_2)} \biggr]
\biggr\}_{\xi_2 = \gamma_i}^{\xi_2 = \Gamma_i} \, .
</math>
|
|
|
<math>~\Phi_i(a,Z_0)</math>
|
<math>~=</math>
|
<math>~\frac{2^{5/2} G \rho_0 a^{2}}{3}
\int\limits_{\xi_1 = \lambda_i}^{\xi_1 = \Lambda_i} \frac{(\xi_1+1)^{1/2}K(\mu) d\xi_1}{(\xi_1^2 - 1)^2 [ (\xi_1^2 - 1)^{1/2}+\xi_1 ]^{1/2} }
\biggr[ \frac{\sin \theta(5\xi_1^2 - 4\xi_1 \cos \theta - 1)}{(\xi_1+1)^{1/2} (\xi_1 - \cos \theta)^{3/2}}
</math>
|
|
|
|
<math>~ - 4\xi_1 E\biggl( \frac{\pi-\theta}{2} \, , \sqrt{\frac{2}{\xi_1 + 1}} \biggr)
+ (\xi_1-1) F\biggl( \frac{\pi-\theta}{2} \, , \sqrt{\frac{2}{\xi_1 + 1}} \biggr) \biggr]_{\theta = \cos^{-1}(\gamma_i)}^{\theta = \cos^{-1}(\Gamma_i)} \, .
</math>
|
|
See Also