Virial Equilibrium of Adiabatic Spheres (Summary)

The summary presented here has been drawn from our accompanying detailed analysis of the structure of pressure-truncated polytropes.

Detailed Force-Balanced Solution

As has been discussed in detail in another chapter, Horedt (1970), Whitworth (1981) and Stahler (1983) have separately derived what the equilibrium radius, <math>~R_\mathrm{eq}</math>, is of a polytropic sphere that is embedded in an external medium of pressure, <math>~P_e</math>. Their solution of the detailed force-balanced equations provides a pair of analytic expressions for <math>~R_\mathrm{eq}</math> and <math>~P_e</math> that are parametrically related to one another through the Lane-Emden function, <math>~\theta</math>, and its radial derivative. For example — see our related discussion for more details — from Horedt's work we obtain the following pair of equations:

<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = r_a \cdot \biggl( \frac{R_\mathrm{Horedt}}{R_\mathrm{norm}} \biggr) </math>	<math>~=~</math>	<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \biggr]^{1/(n-3)} \, , </math>
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} = p_a \cdot \biggl( \frac{P_\mathrm{Horedt}}{P_\mathrm{norm}} \biggr) </math>	<math>~=~</math>	<math> \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \, , </math>

where we have introduced the normalizations,

<math>~R_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math>
<math>~P_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, .</math>

In the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the isolated polytrope, but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the embedded polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Horedt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated isolated (and untruncated) polytrope.

From these previously published works, it is not obvious how — or even whether — this pair of parametric equations can be combined to directly show how the equilibrium radius depends on the value of the external pressure. Our examination of the free-energy of these configurations and, especially, an application of the viral theorem shows this direct relationship. Foreshadowing these results, we note that,

<math>~\biggl[ \biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4\biggr]_\mathrm{Horedt} </math>

<math> \biggl[ \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \biggr] \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{2} \, ; </math>

or, given that <math>~P_\mathrm{norm}R_\mathrm{norm}^4 = GM_\mathrm{tot}^2</math>, this can be rewritten as,

<math>~\biggl[ \frac{P_e R_\mathrm{eq}^4}{G M_\mathrm{limit}^2} \biggr]_\mathrm{Horedt} </math>

<math> \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \, . </math>

Free Energy Function and Virial Theorem

The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following,

Algebraic Free-Energy Function

<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} +~ \frac{1}{(\gamma - 1)} \mathcal{B} \chi^{3-3\gamma} +~ \mathcal{D}\chi^3 \, . </math>

In this expression, the size of the configuration is set by the value of the dimensionless radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>; as is clarified, below, the values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, characterize the relative importance, respectively, of the gravitational potential energy and the internal thermal energy of the configuration; <math>~\gamma</math> is the exponent (from the adopted equation of state) that identifies the adiabat along which the configuration heats or cools upon expansion or contraction; and the relative importance of the imposed external pressure is expressed through the free-energy expression's third constant coefficient, specifically,

<math>~\mathcal{D} \equiv \frac{4\pi}{3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, .</math>

When examining a range of physically reasonable configuration sizes for a given choice of the constants <math>~(\gamma, \mathcal{A}, \mathcal{B}, \mathcal{D})</math>, a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> will often reveal one or two extrema. Each extremum is associated with an equilibrium radius, <math>~\chi_\mathrm{eq} \equiv R_\mathrm{eq}/R_\mathrm{norm}</math>.

Equilibrium Adiabatic Pressure-Radius Diagram

Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our accompanying detailed analysis of the structure of pressure-truncated polytropes, we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following,

Algebraic Expression of the Virial Theorem

<math> \Pi_\mathrm{ad} = \frac{(\Chi_\mathrm{ad}^{4-3\gamma} - 1)}{\Chi_\mathrm{ad}^4} \, , </math>

where, after setting <math>~\gamma = (n+1)/n</math>,

<math>~\Pi_\mathrm{ad}</math>	<math>~=</math>	<math> ~\mathcal{D} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr]^{1/(n-3)} \, , </math> and,
<math>~\Chi_\mathrm{ad}</math>	<math>~=</math>	<math> ~\chi_\mathrm{eq} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \, . </math>

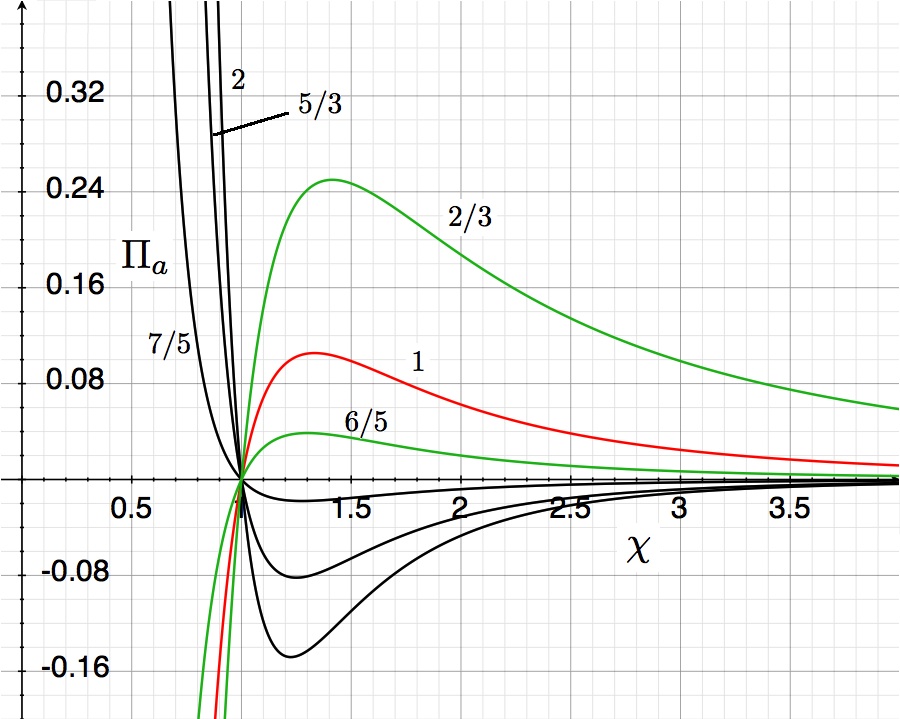
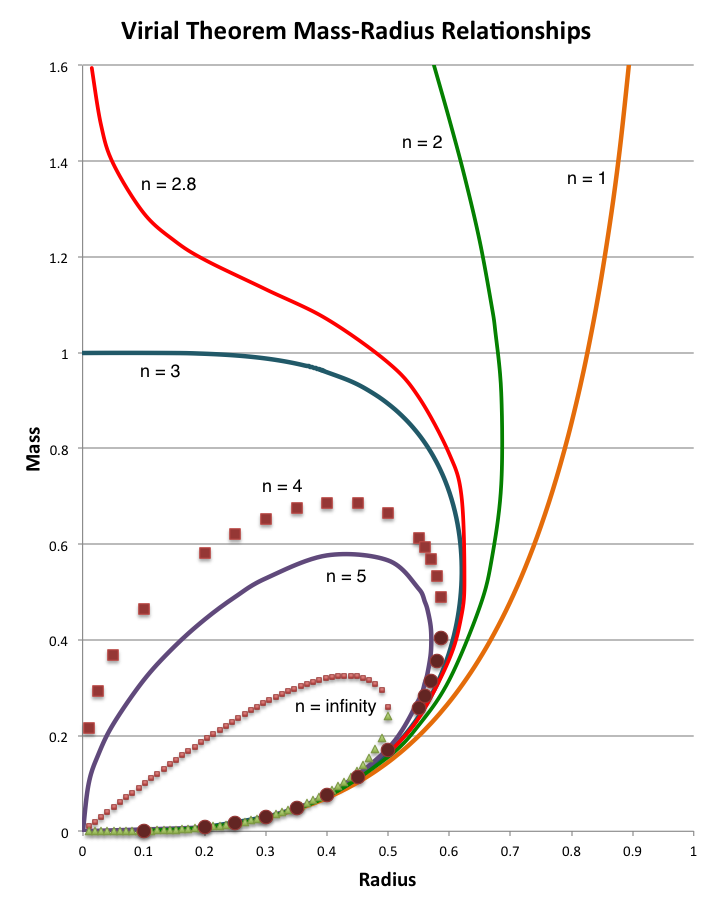
The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\Chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative.

If we multiply the above free=energy function through by an appropriate combination of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, and make the substitution, <math>~\gamma \rightarrow (n+1)/n</math>, it also takes on a particularly simple form featuring the newly defined dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, and the newly identified dimensionless radius, <math>~\Chi \equiv \chi(\mathcal{B}/\mathcal{A})^{n/(n-3)}</math>. Specifically, we obtain the,

Renormalized Free-Energy Function

<math> \mathfrak{G}^{**} \equiv \mathfrak{G}^* \biggl[ \frac{\mathcal{A}^3}{\mathcal{B}^n} \biggr]^{1/(n-3)} = -3 \Chi^{-1} +~ n\Chi^{-3/n} +~ \Pi_\mathrm{ad}\Chi^3 \, . </math>

Relationship to Detailed Force-Balanced Models

Structural Form Factors

In our accompanying detailed analysis, we demonstrate that the expressions given above for the free-energy function and the virial theorem are correct in sufficiently strict detail that they can be used to precisely match — and assist in understanding — the equilibrium of embedded polytropes whose structures have been determined from the set of detailed force-balance equations. In order to draw this association, it is only necessary to realize that, very broadly, the constant coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, in the above algebraic free-energy expression are expressible in terms of three structural form factors, <math>~\tilde\mathfrak{f}_M</math>, <math>~\tilde\mathfrak{f}_W</math>, and <math>~\tilde\mathfrak{f}_A</math>, as follows:

<math>~\mathcal{A}</math>	<math>~\equiv</math>	<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^2 \cdot \tilde\mathfrak{f}_W \, ,</math>
<math>~\mathcal{B}</math>	<math>~\equiv</math>	<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} \cdot \tilde\mathfrak{f}_A = \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3(n+1)/n} \biggr]_\mathrm{eq} \cdot \tilde\mathfrak{f}_A \, ; </math>

and that, specifically in the context of spherically symmetric, pressure-truncated polytropes, we can write,

<math>~\tilde\mathfrak{f}_M</math>	<math>~=</math>	<math>~ \biggl[ - \frac{3\tilde\theta^'}{\tilde\xi} \biggr] \, ,</math>
<math>\tilde\mathfrak{f}_W </math>	<math>~=</math>	<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\tilde\theta^'}{\tilde\xi} \biggr]^2 \, ,</math>
<math>\tilde\mathfrak{f}_A </math>	<math>~=</math>	<math> \frac{3(n+1) }{(5-n)} ~\biggl[ \tilde\theta^' \biggr]^2 + \tilde\theta^{n+1} \, . </math>

After plugging these nontrivial expressions for <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> into the righthand sides of the above equations for <math>~\Pi_\mathrm{ad}</math> and <math>~\Chi_\mathrm{ad}</math> and, simultaneously, using Horedt's detailed force-balanced expressions for <math>~r_a</math> and <math>~p_a</math> to specify, respectively, <math>~\chi_\mathrm{eq}</math> and <math>~P_e/P_\mathrm{norm}</math> in these same equations, we find that,

<math>~\Pi_\mathrm{ad}</math>	<math>~=</math>	<math>~\eta_\mathrm{ad} (1 + \eta_\mathrm{ad})^{-4n/(n-3)} \, ,</math>
<math>~\Chi_\mathrm{ad}</math>	<math>~=</math>	<math>~(1 + \eta_\mathrm{ad})^{n/(n-3)} \, ,</math>

where the newly identified, key physical parameter,

<math>~\eta_\mathrm{ad} </math>

<math>~\equiv</math>

<math>~\frac{(5-n) \tilde\theta^{n+1}}{3(n+1) (\tilde\theta^')^2} \, .</math>

It is straightforward to show that this more compact pair of expressions for <math>~\Pi_\mathrm{ad}</math> and <math>~\Chi_\mathrm{ad}</math> satisfy the virial theorem presented above.

Physical Meaning of Parameter <math>~\eta_\mathrm{ad}</math>

As defined in our above discussion, <math>~\eta_\mathrm{ad}</math> is the ratio of the two terms that are summed together in the definition of the structural form factor, <math>~\tilde\mathfrak{f}_A</math>. It is worth pointing out what physical quantities are associated with these two terms.

At any radial location within a polytropic configuration, the Lane-Emden function, <math>~\theta</math>, is defined in terms of a ratio of the local density to the configuration's central density, specifically,

<math>\theta \equiv \biggl(\frac{\rho}{\rho_c} \biggr)^{1/n} \, .</math>

Remembering that, at any location within the configuration, the pressure is related to the density via the polytropic equation of state,

we see that,

<math>\frac{P}{P_c} = \theta^{n+1} \, .</math>

Hence, the quantity, <math>~\tilde\theta^{n+1}</math>, which appears as the second term in our definition of <math>~\tilde\mathfrak{f}_A</math>, is the ratio, <math>~(P/P_c)_{\tilde\xi}</math>, evaluated at the surface of the truncated polytropic sphere. But, by construction, the pressure at this location equals the pressure of the external medium in which the polytrope is embedded, so we can write,

<math>\tilde\theta^{n+1} = \frac{P_e}{P_c} \, .</math>

In our accompanying detailed analysis, we have employed the virial theorem expression to demonstrate that the first term in our definition of <math>~\tilde\mathfrak{f}_A</math> provides a measure the configuration's normalized central pressure. Specifically, we show that,

<math>~\biggl( \frac{4\pi}{3} \biggr) \frac{P_c R_\mathrm{eq}^4}{G M_\mathrm{limit}^2}</math>

<math>~[3 (n+1) (\tilde\theta^')^2]^{-1} \, .</math>

We conclude, therefore, that quite generally,

<math>(5-n) \tilde\mathfrak{f}_A </math>	<math>~=</math>	<math> \biggl( \frac{3}{4\pi} \biggr) \frac{G M_\mathrm{limit}^2}{P_c R_\mathrm{eq}^4} + (5-n) \frac{P_e}{P_c} </math>
	<math>~=</math>	<math> \biggl( \frac{3}{4\pi} \biggr) \frac{G M_\mathrm{limit}^2}{P_c R_\mathrm{eq}^4} \biggl[1 + \eta_\mathrm{ad} \biggr] \, , </math>

and that,

<math>~\eta_\mathrm{ad} </math>

<math>\biggl[ \frac{4\pi (5-n)}{3} \biggr] \frac{P_e R_\mathrm{eq}^4}{G M_\mathrm{limit}^2} \, .</math>

Desired Pressure-Radius Relation

It is now clear from our review, above, of Horedt's detailed force-balanced solution, that

<math>\frac{4\pi (5-n)}{3}\biggl[\frac{P_e R_\mathrm{eq}^4}{G M_\mathrm{limit}^2} \biggr]_\mathrm{Horedt} </math>

<math>~\eta_\mathrm{ad} \, .</math>

Hence, the pair of parametric equations obtained via a solution of the detailed force-balanced equations satisfy our, slightly rearranged,

Algebraic Expression of the Virial Theorem

<math> \Pi_\mathrm{ad} \Chi_\mathrm{ad}^4 = \Chi_\mathrm{ad}^{(n-3)/n} - 1 \, . </math>

More to the point, it is now clear that this virial theorem expression provides the direct relationship between the configuration's dimensionless equilibrium radius as defined by Horedt, <math>~r_a</math>, and the dimensionless applied external pressure as defined by Horedt, <math>~p_a</math>, that was not apparent from the original pair of parametric relations. Horedt's parameters, <math>~r_a</math> and <math>~p_a</math>, can be directly associated to our parameters, <math>~\Chi_\mathrm{ad}</math> and <math>~\Pi_\mathrm{ad}</math>, via two new normalizations, <math>~r_n</math> and <math>~p_n</math>, defined through the relations,

<math>~\Chi_\mathrm{ad} = \frac{r_a}{r_n}</math>

and

<math>~\Pi_\mathrm{ad} = \frac{p_a}{p_n} \, .</math>

Specifically in terms of the coefficients in the free-energy expression,

<math>~\equiv</math>

<math>~ \frac{(n+1)^n}{4\pi} \biggl[ \mathcal{A} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} \biggr]^n \biggl[ \mathcal{B} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-(n+1)/n} \biggr]^{-n} \, , </math>

and,

<math>~\equiv</math>

<math>~ \frac{3^{n-3}}{(4\pi)^4 (n+1)^{3(n+1)}} \biggl[ \mathcal{A} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} \biggr]^{-3(n+1)} \biggl[ \mathcal{B} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-(n+1)/n} \biggr]^{4n} \, ; </math>

while, in terms of the structural form factors,

<math>~\equiv</math>

<math>~ \frac{1}{3} \biggl[ \frac{(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A} \biggr]^n \mathfrak{f}_M^{1-n} \, , </math>

and,

<math>~\equiv</math>

<math>~ \frac{1}{(4\pi)^8} \biggl[ \frac{3\cdot 5^3}{(n+1)^3} \cdot \frac{\mathfrak{f}_M^2}{\mathfrak{f}_W^3} \biggr]^{n+1} \mathfrak{f}_A^{4n} \, . </math>

Discussion

Model Sequences

Equilibrium Adiabatic Pressure-Radius Diagram

After choosing a value for the system's adiabatic index (or, equivalently, its polytropic index), <math>~\gamma = (n+1)/n</math>, the functional form of the virial theorem expression, <math>~\Pi_\mathrm{ad}(\chi_\mathrm{ad})</math>, is known and, hence, the equilibrium model sequence can be plotted. Half-a-dozen such model sequences are shown in the figure near the beginning of this discussion. Each curve can be viewed as mapping out a single-parameter sequence of equilibrium models; "evolution" along the curve can be accomplished by varying the key parameter, <math>~\eta_\mathrm{ad}</math>, over the physically relevant range, <math>0 \le \eta_\mathrm{ad} < \infty</math>. To simplify our discussion, here, we redisplay the above figure and repeat a few key algebraic relations.

<math>~\eta_\mathrm{ad} </math>	<math>~\equiv</math>	<math>~\frac{(5-n) \tilde\theta^{n+1}}{3(n+1) (\tilde\theta^')^2} = \biggl[ \frac{4\pi (5-n)}{3} \biggr] \frac{P_e R_\mathrm{eq}^4}{G M_\mathrm{limit}^2}\, ,</math>
<math>~\Pi_\mathrm{ad}</math>	<math>~=</math>	<math>~\eta_\mathrm{ad} (1 + \eta_\mathrm{ad})^{-4n/(n-3)} \, ,</math>
<math>~\Chi_\mathrm{ad}</math>	<math>~=</math>	<math>~(1 + \eta_\mathrm{ad})^{n/(n-3)} \, ,</math>

When <math>~\eta_\mathrm{ad}</math> is zero

For the types of systems that are presently most relevant to astrophysical discussions, the key parameter, <math>~\eta_\mathrm{ad}</math>, can be zero for one of two reasons: Either <math>~n=5</math>; or <math>~\tilde\theta \rightarrow \theta_{\xi_1} = 0</math>. In the latter case, all curves converge on the same point, that is, <math>~(\Chi_\mathrm{ad}, \Pi_\mathrm{ad}) = (1, 0)</math>. This corresponds to the case of no external medium <math>~(P_e = 0)</math> and, hence, the associated equilibrium configuration is the familiar isolated polytropic sphere. As can be deduced from our above discussion of the algebraic expression of the virial theorem, because <math>~\Chi_\mathrm{ad} = 1</math>, the equilibrium radius of such a configuration is,

<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = \chi_\mathrm{eq}</math>

<math>~\biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{n/(n-3)} \, .</math>

As is demonstrated in an accompanying discussion and also mentioned above, after inserting the relevant expressions for the free-energy coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, this provides the key relationship between the mass, equilibrium radius, and central pressure of an isolated polytrope, namely,

<math>~\frac{P_c R_\mathrm{eq}^4}{G M_\mathrm{limit}^2}</math>

<math>~\frac{1}{[4\pi (n+1) (\theta^')^2]_{\xi_1}} \, .</math>

As we have reviewed elsewhere — see also our detailed discussion of isolated polytropes — this is a familiar relationship, appearing prominently in Chapter IV (p. 99, equations 80 and 81) of Chandrasekhar [C67] in association with his discussion of the dimensionless coefficient, <math>~W_n</math>, and the central pressure of polytropes.

In the former case — that is, in the case where <math>~\eta_\mathrm{ad} \rightarrow 0</math> because the chosen polytropic index is, <math>~n=5</math> — it must be the case that <math>~\Chi_\mathrm{ad} = 1</math> along the entire sequence (see the green curve labeled <math>~\gamma = (n+1)/n = 6/5</math> in the accompanying figure). This means that the expression for the central pressure,

<math>~\frac{P_c R_\mathrm{eq}^4}{G M_\mathrm{limit}^2}</math>

<math>~\frac{1}{[4\pi (n+1) (\tilde\theta^')^2]} \, ,</math>

does not explicitly depend on the size of the applied external pressure. But the central pressure does depend on the radial location at which the configuration is truncated, via the parameter <math>~\tilde\theta^'</math>, which is evaluated at <math>~\tilde\xi</math>, rather than at <math>~\xi_1</math>.

Stability

Analysis of the free-energy function allows us to not only ascertain the equilibrium radius of isolated polytropes and pressure-truncated polytropic configurations, but also the relative stability of these configurations. We begin by repeating the,

Renormalized Free-Energy Function

<math> \mathfrak{G}^{**} = -3 \Chi^{-1} +~ n\Chi^{-3/n} +~ \Pi_\mathrm{ad}\Chi^3 \, . </math>

The first and second derivatives of <math>~\mathfrak{G}^{**}</math>, with respect to the dimensionless radius, <math>~\Chi</math>, are, respectively,

<math>~\frac{\partial\mathfrak{G}^{**}}{\partial\Chi}</math>	<math>~=</math>	<math>~3 \Chi^{-2} -3\Chi^{-(n+3)/n} + 3\Pi_\mathrm{ad} \Chi^2 \, ,</math>
<math>~\frac{\partial^2\mathfrak{G}^{**}}{\partial\Chi^2}</math>	<math>~=</math>	<math>~-6 \Chi^{-3} + \frac{3(n+3)}{n} \Chi^{-(2n+3)/n} + 6\Pi_\mathrm{ad} \Chi \, .</math>

As alluded to, above, equilibrium radii are identified by values of <math>~\Chi</math> that satisfy the equation, <math>\partial\mathfrak{G}^{**}/\partial\Chi = 0</math>. Specifically, marking equilibrium radii with the subscript "ad", they will satisfy the

Algebraic Expression of the Virial Theorem

<math> \Pi_\mathrm{ad} = \frac{\Chi_\mathrm{ad}^{(n-3)/n} - 1}{\Chi_\mathrm{ad}^4} \, . </math>

Dynamical stability then depends on the sign of the second derivative of <math>~\mathfrak{G}^{**}</math>, evaluated at the equilibrium radius; specifically, configurations will be stable if,

<math>~\frac{\partial^2\mathfrak{G}^{**}}{\partial\Chi^2}\biggr|_{\Chi_\mathrm{ad}}</math>

<math>~0 \, ,</math> (stable)

and they will be unstable if, upon evaluation at the equilibrium radius, the sign of the second derivative is less than zero. Hence, isolated polytropes as well as pressure-truncated polytropic configurations will be stable if,

<math>~0</math>	<math>~< </math>	<math>~3 \Chi_\mathrm{ad}^{-3} \biggl[ - 2 + \frac{(n+3)}{n} \Chi_\mathrm{ad}^{(n-3)/n} + 2\Pi_\mathrm{ad} \Chi_\mathrm{ad}^4 \biggr]</math>
	<math>~< </math>	<math>~3 \Chi_\mathrm{ad}^{-3} \biggl\{ \frac{(n+3)}{n} \Chi_\mathrm{ad}^{(n-3)/n} + 2[\Chi_\mathrm{ad}^{(n-3)/n} -1] - 2\biggr\}</math>
	<math>~< </math>	<math>~3 \Chi_\mathrm{ad}^{-3} \biggl[ \frac{3(n+1)}{n} \Chi_\mathrm{ad}^{(n-3)/n} - 4\biggr]</math>
<math>\Rightarrow~~~~\Chi_\mathrm{ad}</math>	<math>~> </math>	<math>~\biggl[ \frac{4n}{3(n+1)} \biggr]^{n/(n-3)} \, .</math> (stable)

Reference to this stability condition proves to be simpler if we define the limiting configuration size as,

<math>~\Chi_\mathrm{min} \equiv \biggl[ \frac{4n}{3(n+1)} \biggr]^{n/(n-3)} \, ,</math>

and write the stability condition as,

<math>~\Chi_\mathrm{ad} > \Chi_\mathrm{min} \, .</math> (stable)

When examining the equilibrium sequences found in the upper-righthand quadrant of the figure at the top of this page — each corresponding to a different value of the polytropic index, <math>~n > 3</math> or <math>~n < 0</math> — we find that <math>~\Chi_\mathrm{min}</math> corresponds to the location along each sequence where the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, reaches a maximum. (Keeping in mind that the virial theorem defines each of these sequences, this statement of fact can be checked by identifying where the condition, <math>~\partial\Pi_\mathrm{ad}/\partial\Chi_\mathrm{ad} = 0</math>, occurs according to the algebraic expression of the virial theorem.) Hence, we conclude that, along each sequence, no equilibrium configurations exist for values of the dimensionless external pressure that are greater than,

<math>~\Pi_\mathrm{max}</math>	<math>~\equiv</math>	<math>~\Chi_\mathrm{min}^{-4} \biggl[ \Chi_\mathrm{min}^{(n-3)/n} - 1 \biggr] </math>
	<math>~=</math>	<math>~\biggl[ \frac{3(n+1)}{4n} \biggr]^{4n/(n-3)} \biggl[\frac{4n}{3(n+1)} - 1 \biggr]</math>
	<math>~=</math>	<math>~\biggl\{ \biggl[ \frac{3(n+1)}{4n} \biggr]^{4n} \biggl[\frac{n-3}{3(n+1)} \biggr]^{n-3} \biggr\}^{1/(n-3)}</math>
<math>~\Rightarrow~~~~\Pi_\mathrm{max}^{n-3}</math>	<math>~=</math>	<math>~(4n)^{-4n}~[3(n+1)]^{3(n+1)} ~(n-3)^{n-3} \, .</math>

In the context of a general examination of the free-energy of pressure-truncated polytropes, it is worth noting that this limit on the external pressure also establishes a limit on the coefficient, <math>~\mathcal{D}</math>, that appears in the free energy function. Specifically, we will not expect to find any extrema in the free energy if,

<math>~\mathcal{D} > \mathcal{D}_\mathrm{max}</math>

<math>~\equiv</math>

<math>~(n-3) \biggl\{ \biggl[ \frac{\mathcal{B}}{4n} \biggr]^{4n}~\biggl[ \frac{3(n+1)}{\mathcal{A}} \biggr]^{3(n+1)} ~\biggr\}^{1/(n-3)} \, .</math>

Finally, it is worth noting that the point along each equilibrium sequence that is identified by the coordinates, <math>~(\Chi_\mathrm{min}, \Pi_\mathrm{max})</math> always corresponds to,

<math>~\eta_\mathrm{ad} = \eta_\mathrm{crit} \equiv \frac{n-3}{3(n+1)} \, .</math>

Summary

<math>~\eta_\mathrm{crit}</math>	<math>~\equiv</math>	<math>~ \frac{n-3}{3(n+1)} </math>
<math>~\Pi_\mathrm{max}</math>	<math>~\equiv</math>	<math>~(n-3) \biggl\{~\frac{ [3(n+1)]^{3(n+1)} }{(4n)^{4n}} \biggr\}^{1/(n-3)} </math>
<math>~\Chi_\mathrm{min} </math>	<math>~\equiv</math>	<math> \biggl[ \frac{4n}{3(n+1)} \biggr]^{n/(n-3)} </math>

Try Polytropic Index of 4

Groundwork

In an effort to more fully understand what can be learned from an examination of the free-energy, let's play with <math>~n=4</math> polytropic models. First, let's plot <math>~\mathfrak{G}^{**}(\Chi)</math> using a specific, trial value of the coefficient, <math>~\Pi_\mathrm{ad}</math>, keeping in mind that,

<math>~\eta_\mathrm{crit}\biggr\|_{n=4}</math>	<math>~=</math>	<math>~\frac{1}{15} = 0.066667 \, ;</math>
<math>~\Pi_\mathrm{max}\biggr\|_{n=4}</math>	<math>~=</math>	<math>~\frac{15^{15}}{16^{16}} = 0.02373828 \, ;</math>
<math>~\Chi_\mathrm{min}\biggr\|_{n=4}</math>	<math>~=</math>	<math>~\biggl( \frac{16}{15} \biggr)^4 = 1.294538 \, .</math>

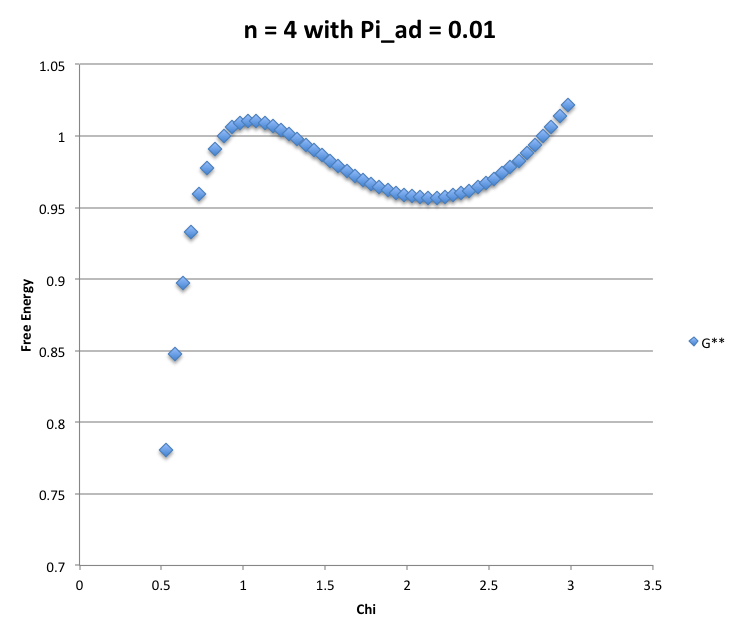
At the top of the table, shown below, we display a plot of the,

Renormalized Free-Energy Function

<math> \mathfrak{G}^{**} = -3 \Chi^{-1} +~ n\Chi^{-3/n} +~ \Pi_\mathrm{ad}\Chi^3 \, , </math>

where we have set <math>~n = 4</math>, and <math>~\Pi_\mathrm{ad} = 0.01</math>. Reading quantities off of the plot, the left and right extrema identify equilibria having the following approximate dimensionless radii: <math>~\Chi_\mathrm{left} \approx 1.03</math> and <math>~\Chi_\mathrm{right} \approx 2.13</math>. Upon closer examination (plots not shown), we have determined that, <math>~\Chi_\mathrm{left} \approx 1.0494</math> and <math>~\Chi_\mathrm{right} \approx 2.13905</math>. In accordance with our stability analysis, these values of <math>~\Chi_\mathrm{ad}</math> fall on either side of the demarcation value, <math>~\Chi_\mathrm{min} = (16/15)^4</math>, with the one on the left being a local maximum in the free energy — indicating an unstable equilibrium — while the one on the right is a local minimum — indicating a stable equilibrium. Next, let's check to see if both extrema satisfy the,

Algebraic Expression of the Virial Theorem

<math> \Pi_\mathrm{ad} = \frac{\Chi_\mathrm{ad}^{(n-3)/n} - 1}{\Chi_\mathrm{ad}^4} \, . </math>

For the unstable equilibrium configuration, we calculate,

<math>\Pi_\mathrm{ad} \approx [(1.0494)^{1/4} - 1]/(1.0494)^4 = 1.000024 \times 10^{-2}</math>;

while, for the stable equilibrium we calculate,

<math>\Pi_\mathrm{ad} \approx [(2.13905)^{1/4} - 1]/(2.13905)^4 = 1.000018 \times 10^{-2}</math>.

Because we inserted a value of <math>~\Pi_\mathrm{ad} = 0.01</math> into the free-energy expression, we conclude that, as desired, both identified extrema satisfy the virial relation to the measured accuracy. These parameter values, and the corresponding values of many other related physical parameters are summarized in the following table, along with the algebraic relations that were used to calculate them.

First Table


Determined from Plot of Renormalized Free-Energy with <math>~(n, \Pi_\mathrm{ad}) = (4, 0.01)</math>
		Maximum	Minimum
	<math>~\Chi</math>	<math>~1.0494</math>	<math>~2.13905</math>
Immediate Implications from Virial Theorem
<math>~\Chi^{1/4} - 1</math>	<math>~\eta_\mathrm{ad}</math>	<math>~0.012128</math>	<math>~0.20936</math>
<math>~(\Chi^{1/4} - 1)\cdot \Chi^{-4}</math>	<math>~\Pi_\mathrm{ad}</math>	<math>~1.000024 \times 10^{-2}</math>	<math>~1.000018 \times 10^{-2}</math>
Associated Detailed Force-Balanced Model Parameters obtained via interpolation of tabulated numbers on p. 399 of Horedt (1986, ApJS, vol. 126)
	<math>~\tilde\xi</math> (approx.)	<math>~4.81</math>	<math>~1.624</math>
	<math>~\tilde\theta</math> (approx.)	<math>~0.251</math>	<math>~0.709</math>
	<math>~- \tilde\theta^'</math> (approx.)	<math>~0.0727</math>	<math>~0.239</math>
<math>~\frac{1}{15}\cdot \frac{\tilde\theta^5}{(\tilde\theta^')^2}</math>	<math>~\eta</math> (check)	<math>~0.0126</math>	<math>~0.2091</math>
and, hence, Implied Structural Form Factors & Coefficients <math>~\mathcal{B}</math> & <math>~\mathcal{A}</math>
<math>~3(-\tilde\theta^')/\tilde\xi</math>	<math>~\mathfrak{f}_M</math>	<math>~0.0453</math>	<math>~0.4415</math>
<math>~5[3(-\tilde\theta^')/\tilde\xi]^2</math>	<math>~\mathfrak{f}_W</math>	<math>~0.01028</math>	<math>~0.975</math>
<math>~15(-\tilde\theta^')^2 + \tilde\theta^5</math>	<math>~\mathfrak{f}_A</math>	<math>~0.08028</math>	<math>~1.036</math>
<math>~\biggl(\frac{3}{4\pi} \biggr)^{1/4} \mathfrak{f}_M^{-5/4} \cdot \mathfrak{f}_A</math>	<math>~\mathcal{B}</math>	<math>~2.682</math>	<math>~2.0122</math>
<math>~\frac{\tilde\mathfrak{f}_W}{5 \tilde\mathfrak{f}_M^2} </math>	<math>~\mathcal{A}</math>	<math>~1</math>	<math>~1</math>
Given <math>~\Pi_\mathrm{ad}</math>, <math>~\Chi</math>, and <math>~\mathcal{B}</math>, we obtain
<math>~\frac{3}{4\pi}\mathcal{D} = \frac{3}{4\pi} \Pi_\mathrm{ad} \mathcal{B}^{16} </math>	<math>~\frac{P_e}{P_\mathrm{norm}}</math>	<math>~1.71 \times 10^4</math>	<math>~1.72 \times 10^2</math>
<math>~\Chi \mathcal{B}^{-4}</math>	<math>~\chi_\mathrm{eq}</math>	<math>~0.0203</math>	<math>~0.1305</math>
Compare with Horedt's Equilibrium Parameters obtained from DFB Models
<math>\biggl[ \biggl( \frac{5^3}{4\pi} \biggr) \tilde\theta( -\tilde\xi^2 \tilde\theta' )^{2} \biggr]^{5} </math>	<math>~\frac{P_e}{P_\mathrm{norm}}</math>	<math>~1.76 \times 10^4</math>	<math>~1.73 \times 10^2</math>
<math> \biggl( \frac{4\pi}{5^4} \biggr) \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{-3} </math>	<math>~\chi_\mathrm{eq}</math>	<math>~0.0203</math>	<math>~0.130</math>

Now, we are convinced that both extrema identify perfectly valid equilibrium configurations. However, in the context of astrophysics, the two identified equilibria are not connected to one another in any meaningful way. In particular, two of the free-energy coefficients, <math>~\mathcal{B}</math> and <math>~\mathcal{D}</math>, have different values in the two cases; and, by inference, the normalized external pressure, <math>~P_e/P_\mathrm{norm}</math>, is different in the two cases. So the plotted free-energy curve does not represent a "constant pressure" evolutionary trajectory. How do we identify two equilibria that are associated with the same normalized external pressure? And how do we identify the free-energy "evolutionary trajectory" that connects the two states?

Second Table

Here, we have decided to look for a stable equilibrium state that is bounded by the same external pressure as the unstable state that has been identified in the above figure and table. Rather than going straight to the free-energy expression in search of the desired stable configuration, we cheated a bit. Using the properties of an <math>~n=4</math> polytrope, as tabulated on p. 399 of Horedt (1986, ApJS, vol. 126), in conjunction with the algebraic expression found in the next-to-last row of the above table, namely,

<math> \frac{P_e}{P_\mathrm{norm}} = \biggl[ \biggl( \frac{5^3}{4\pi} \biggr) \tilde\theta( -\tilde\xi^2 \tilde\theta' )^{2} \biggr]^{5} \, , </math>

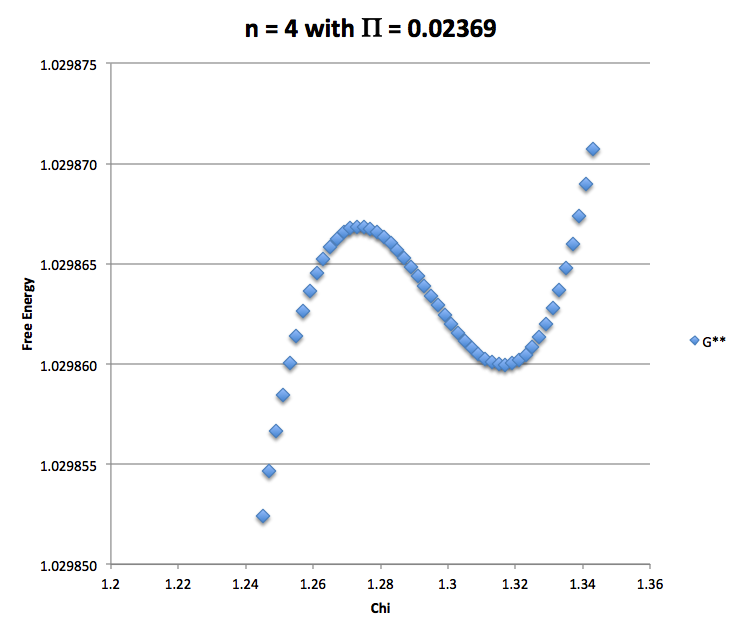
we examined how <math>~P_e</math> varies with <math>~\tilde\xi</math>. We found that <math>~P_e/P_\mathrm{norm} = 1.71\times 10^4</math> at <math>~\tilde\xi = 2.6</math>, which is almost identical to the value of the normalized external pressure that we determined was associated with the unstable equilibrium state (at <math>~\tilde\xi = 4.81</math>) above. As is illustrated by the figure and table that follows, we determined that the stable equilibrium state associated with this normalized external pressure is the minimum that occurs on the free energy curve having parameters, <math>~(n, \Pi_\mathrm{ad}) = (4, 0.02369)</math>.


Determined from Plot of Renormalized Free-Energy with <math>~(n, \Pi_\mathrm{ad}) = (4, 0.02369)</math>
		Maximum	Minimum
	<math>~\Chi</math>	<math>~1.274</math>	<math>~1.317</math>
Immediate Implications from Virial Theorem
<math>~\Chi^{1/4} - 1</math>	<math>~\eta_\mathrm{ad}</math>	<math>~0.0624</math>	<math>~0.0713</math>
<math>~(\Chi^{1/4} - 1)\cdot \Chi^{-4}</math>	<math>~\Pi_\mathrm{ad}</math>	<math>~0.02369</math>	<math>~0.02369 </math>
Associated Detailed Force-Balanced Model Parameters obtained via interpolation of tabulated numbers on p. 399 of Horedt (1986, ApJS, vol. 126)
	<math>~\tilde\xi</math> (approx.)	----	<math>~2.6</math>
	<math>~\tilde\theta</math> (approx.)	----	<math>~0.5048</math>
	<math>~- \tilde\theta^'</math> (approx.)	----	<math>~0.175</math>
<math>~\frac{1}{15}\cdot \frac{\tilde\theta^5}{(\tilde\theta^')^2}</math>	<math>~\eta</math> (check)	----	<math>~0.0714</math>
and, hence, Implied Structural Form Factors & Coefficients <math>~\mathcal{B}</math> & <math>~\mathcal{A}</math>
<math>~3(-\tilde\theta^')/\tilde\xi</math>	<math>~\mathfrak{f}_M</math>	----	<math>~0.2019</math>
<math>~5[3(-\tilde\theta^')/\tilde\xi]^2</math>	<math>~\mathfrak{f}_W</math>	----	<math>~0.2039</math>
<math>~15(-\tilde\theta^')^2 + \tilde\theta^5</math>	<math>~\mathfrak{f}_A</math>	----	<math>~0.4922</math>
<math>~\biggl(\frac{3}{4\pi} \biggr)^{1/4} \mathfrak{f}_M^{-5/4} \cdot \mathfrak{f}_A</math>	<math>~\mathcal{B}</math>	----	<math>~2.542</math>
<math>~\frac{\tilde\mathfrak{f}_W}{5 \tilde\mathfrak{f}_M^2} </math>	<math>~\mathcal{A}</math>	<math>~1</math>	<math>~1</math>
Given <math>~\Pi_\mathrm{ad}</math>, <math>~\Chi</math>, and <math>~\mathcal{B}</math>, we obtain
<math>~\frac{3}{4\pi}\mathcal{D} = \frac{3}{4\pi} \Pi_\mathrm{ad} \mathcal{B}^{16} </math>	<math>~\frac{P_e}{P_\mathrm{norm}}</math>	----	<math>~1.71 \times 10^4</math>
<math>~\Chi \mathcal{B}^{-4}</math>	<math>~\chi_\mathrm{eq}</math>	----	<math>~0.0316</math>
Compare with Horedt's Equilibrium Parameters obtained from DFB Models
<math>\biggl[ \biggl( \frac{5^3}{4\pi} \biggr) \tilde\theta( -\tilde\xi^2 \tilde\theta' )^{2} \biggr]^{5} </math>	<math>~\frac{P_e}{P_\mathrm{norm}}</math>	----	<math>~1.71 \times 10^4</math>
<math> \biggl( \frac{4\pi}{5^4} \biggr) \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{-3} </math>	<math>~\chi_\mathrm{eq}</math>	----	<math>~0.0316</math>

Summary

The algebraic free-energy function associated with pressure-truncated <math>~n=4</math> polytropes is,

<math> \mathfrak{G}^*\biggr|_{n=4} = -3\mathcal{A} \chi^{-1} +~ 4\mathcal{B} \chi^{-3/4} +~ \mathcal{D}\chi^3 \, , </math>

and the corresponding renormalized free-energy function is,

<math> \mathfrak{G}^{**}\biggr|_{n=4} \equiv \mathfrak{G}^* \biggl[ \frac{\mathcal{A}^3}{\mathcal{B}^n} \biggr]^{1/(n-3)} = -3 \Chi^{-1} +~ 4\Chi^{-3/4} +~ \Pi_\mathrm{ad}\Chi^3 \, . </math>

As has been demonstrated, above, the two equilibrium states that are supported by the same external pressure of, <math>~P_e/P_\mathrm{norm} = 1.71 \times 10^4</math>, are associated with extrema found in the following free-energy curves: The unstable equilibrium appears as a relative maximum in the free-energy curves having the coefficient values,

<math>~\Pi_\mathrm{ad} = 0.01</math> or <math>(\mathcal{A}, \mathcal{B}, \mathcal{D}) = (1, 2.682, 7.16\times 10^4) \, .</math>

The stable equilibrium appears as a relative minimum in the free-energy curves having the coefficient values,

<math>~\Pi_\mathrm{ad} = 0.02369</math> or <math>(\mathcal{A}, \mathcal{B}, \mathcal{D}) = (1, 2.542, 7.16\times 10^4) \, .</math>

Configurations Sharing the Same External Pressure

ASIDE: In retrospect, it is obvious that pairs of truncated equilibrium configurations of a given polytropic index that are bounded by the same external pressure — and, hence, that may share a physical evolutionary connection — will share the same value of Horedt's dimensionless pressure,

<math>~\equiv</math>

<math> \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, . </math>

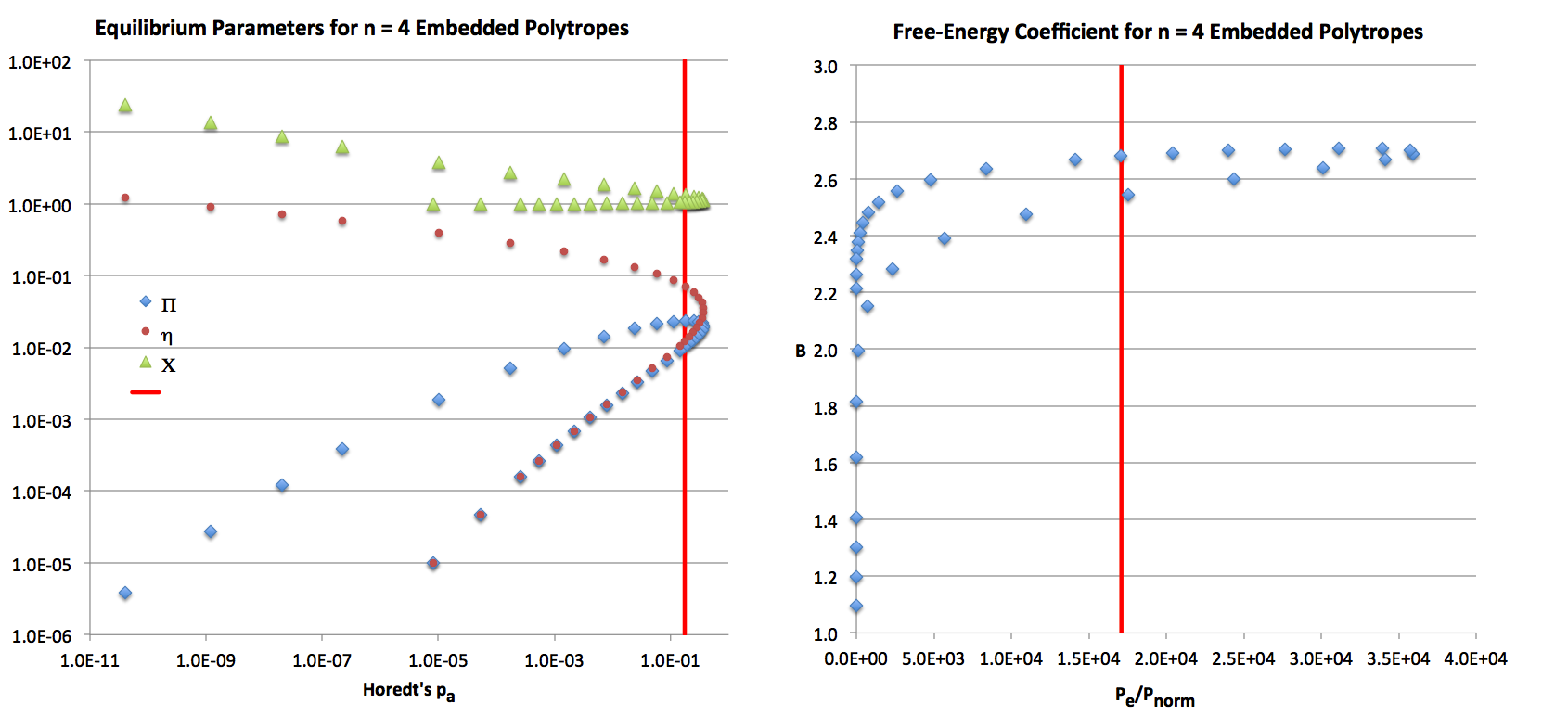
The implication is that a single free-energy curve with constant coefficients cannot connect the two equilibrium states. There are certainly two separate equilibrium states that can be supported by the specified external pressure, but these two states exhibit somewhat different values of the structural form factors, which leads to different values of the coefficient, <math>~\mathcal{B}</math>. The righthand plot in the following figure shows how <math>~\mathcal{B}</math> varies with the applied external pressure in <math>~n=4</math> polytropes.

Variation of Various Physical Parameters along the Sequence of Pressure-Truncated <math>~n=4</math> Polytropes

[Structural data obtained from the table provided on p. 399 of Horedt (1986, ApJS, vol. 126)]

Left: This log-log plot displays the variation with applied external pressure, <math>~p_a</math> (increasing to the right along the horizontal axis), of the renormalized pressure, <math>~\Pi_\mathrm{ad}</math> (light blue diamonds), the renormalized equilibrium radius, <math>~\Chi_\mathrm{ad}</math> (light green triangles), and the key physical parameter, <math>~\eta_\mathrm{ad}</math> (maroon circles). As the diagram illustrates, each parameter is double-valued, demonstrating that, for any choice of the dimensionless external pressure (as long as the pressure is less than a well-defined limiting value), there are two available equilibrium states. Along all three curves, parameter values associated with the stable equilibrium are traced by the upper portion of the curve. The red vertical line has been drawn at the value of <math>~{p_a} = 0.176</math>, corresponding to the external pressure <math>~(P_e/P_\mathrm{norm} = 1.71\times 10^4)</math> examined in the above two tables. This red line intersects the <math>~\Pi(p_a)</math> curve at <math>~\Pi = 0.01</math> (unstable state examined above) and at <math>~\Pi = 0.02369</math> (stable state examined above).

Right: This plot (linear scale on both axes) shows how <math>~\mathcal{B}</math> (curve outlined by light blue diamonds) varies with the applied external pressure, <math>~P_e/P_\mathrm{norm}</math>, in <math>~n=4</math> polytropes. The curve bends back on itself, showing that at any value of <math>~P_e</math>, below some limiting value, two equilibrium configurations exist and they have different values of <math>~\mathcal{B}</math>. The vertical red line identifies the value of the external pressure <math>~(P_e/P_\mathrm{norm} = 1.71\times 10^4)</math> that has been used as an example in the above two tables to illustrate how a pair of physically associated equilibrium states can be identified. This red line intersects the displayed curve at <math>~\mathcal{B} = 2.682</math> (unstable state examined above) and at <math>~\mathcal{B} = 2.542</math> (stable state examined above).

Curiosity

Pressure vs. pressure plot

The figure displayed here, on the right, is a magnification of a segment of the <math>~\Pi(p_a)</math> curve (light blue diamonds) shown in the lefthand panel of the preceding figure, although here we have used a linear, rather than a log, scale on both axes. The quantity being plotted along both axes is the external pressure, but normalized in different ways. The quantity, <math>~p_a</math> (horizontal axis), provides a direct measure of the physical external (hence, also, surface) pressure, while the quantity, <math>~\Pi</math> (vertical axis), is the external pressure renormalized by a specific combination of the free-energy coefficients. Our stability analysis has been conducted assuming that the free-energy coefficients — which are expressible in terms of structural form factors — are constants, that is, they do not vary with the size of the configuration. Hence, it is the limiting value of <math>~\Pi_\mathrm{ad}</math>, specifically,

<math>~\Pi_\mathrm{max}\biggr|_{n=4}</math>

that identifies the demarcation between stable and unstable states. This limiting value is identified by the horizontal red-dashed line in the figure; and the relevant demarcation point appears where this tangent line touches the curve. According to our stability analysis, equilibrium configurations to the left of this demarcation point are stable while configurations to the right are unstable.

In the context of our discussion of the lefthand diagram in the preceding figure — see especially the relevant figure caption — we claimed that, for each physically allowed value of the external pressure, <math>~p_a</math>, the parameter, <math>~\Pi</math>, was double-valued and that configurations along the upper segment of its curve were stable. After studying a magnification of this parameter curve near its turning point, a bit of clarification is required. It appears as though equilibrium models lying along the short upper segment of the curve that falls between the demarcation/tangent point at <math>~\Pi_\mathrm{max}</math> and the maximum value of <math>~p_a</math> are unstable. This means that, even though two equilibrium configurations can be constructed at each value of <math>~p_a</math> in this region near and including the turning point, both configurations are dynamically unstable. We conclude, therefore, that stable configurations only exist for values of <math>~p_a</math> that are less than the value associated with <math>~\Pi_\mathrm{max}</math>.

Mass-Radius Relation

Up to this point in our discussion, we have focused on an analysis of the pressure-radius relationship that defines the equilibrium configurations of pressure-truncated polytropes. In effect, we have viewed the problem through the same lens as did Horedt (1970) and, separately, Whitworth (1981), defining variable normalizations in terms of the polytropic constant, <math>~K</math>, and the configuration mass, <math>~M_\mathrm{tot}</math>, which were both assumed to be held fixed throughout the analysis. Here we switch to the approach championed by Stahler (1983), defining variable normalizations in terms of <math>~K</math> and <math>~P_e</math>, and examining the mass-radius relationship of pressure-truncated polytropes.

Detailed Force-Balanced Solution

As has been summarized in our accompanying review of detailed force-balanced models of pressure-truncated polytropes, Stahler (1983) found that a spherical configuration's equilibrium radius is related to its mass through the following pair of parametric equations:

<math> ~\frac{M_\mathrm{tot}}{M_\mathrm{SWS} } </math>	<math>~=~</math>	<math> \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \tilde\theta^{(n-3)/2} (- \tilde\xi^2 \tilde\theta^') \, , </math>
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } </math>	<math>~=~</math>	<math> \biggl( \frac{n}{4\pi} \biggr)^{1/2} \tilde\xi \tilde\theta^{(n-1)/2} \, , </math>

where,

<math>M_\mathrm{SWS} \equiv \biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math>

<math> R_\mathrm{SWS} \equiv \biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, . </math>

Mapping from Above Discussion

Looking back on the definitions of <math>~\Pi_\mathrm{ad}</math> and <math>~\Chi_\mathrm{ad}</math> that we introduced in connection with our initial concise algebraic expression of the virial theorem, we can write,

<math>~P_e </math>	<math>~=</math>	<math> ~P_\mathrm{norm} \biggl( \frac{3}{4\pi} \biggr) \Pi_\mathrm{ad} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr]^{1/(n-3)} </math>
	<math>~=</math>	<math> ~\biggl( \frac{3}{4\pi} \biggr) \Pi_\mathrm{ad} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr]^{1/(n-3)} \biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, , </math>
<math>~R_\mathrm{eq} </math>	<math>~=</math>	<math> ~R_\mathrm{norm} \Chi_\mathrm{ad} \biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{n/(n-3)} </math>
	<math>~=</math>	<math> ~\Chi_\mathrm{ad} \biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{n/(n-3)} \biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, . </math>

The first of these two expressions can be flipped around to give an expression for <math>~M_\mathrm{tot}</math> in terms of <math>~P_e</math> and, then, as normalized to <math>~M_\mathrm{SWS}</math>. Specifically,

<math>~ M_\mathrm{tot}^{2(n+1)}</math>	<math>~=</math>	<math> ~\biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{n-3} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr] \biggl[ \frac{K^{4n}}{G^{3(n+1)}P_e^{n-3} } \biggr] </math>
	<math>~=</math>	<math> ~M_\mathrm{SWS}^{2(n+1)} \biggl( \frac{n}{n+1} \biggr)^{3(n+1)} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{n-3} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr] </math>
<math>~ \Rightarrow~~~ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}</math>	<math>~=</math>	<math> ~\biggl( \frac{n}{n+1} \biggr)^{3/2} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(n-3)/[2(n+1)]} \biggl[ \frac{\mathcal{B}^{2n/(n+1)}}{\mathcal{A}^{3/2}} \biggr] \, . </math>

This means, as well, that we can rewrite the equilibrium radius as,

<math>~R_\mathrm{eq}^{n-3} </math>	<math>~=</math>	<math> ~\Chi_\mathrm{ad}^{n-3} \biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{n} \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} </math>
	<math>~=</math>	<math> ~\Chi_\mathrm{ad}^{n-3} \biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{n} \biggl( \frac{G}{K} \biggr)^n \biggl\{ \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{n-3} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr] \biggl[ \frac{K^{4n}}{G^{3(n+1)}P_e^{n-3} } \biggr] \biggr\}^{(n-1)/[2(n+1)]} </math>
	<math>~=</math>	<math> ~\Chi_\mathrm{ad}^{n-3} \biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{n} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr]^{(n-1)/[2(n+1)]} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(n-3)(n-1)/[2(n+1)]} \biggl( \frac{G}{K} \biggr)^n \biggl\{ \biggl[ \frac{K^{4n}}{G^{3(n+1)}P_e^{n-3} } \biggr] \biggr\}^{(n-1)/[2(n+1)]} </math>
	<math>~=</math>	<math> ~\Chi_\mathrm{ad}^{n-3} \biggl\{ \biggl[ \frac{\mathcal{A}}{\mathcal{B}} \biggr]^{2n(n+1)} \biggl[ \frac{\mathcal{B}^{4n(n-1)}}{\mathcal{A}^{3(n+1)(n-1)}} \biggr]\biggr\}^{1/[2(n+1)]} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(n-3)(n-1)/[2(n+1)]} \biggl\{ \biggl( \frac{G}{K} \biggr)^{2n(n+1)} \biggl[ \frac{K^{4n(n-1)}}{G^{3(n+1)(n-1)}P_e^{(n-3)(n-1)} } \biggr] \biggr\}^{1/[2(n+1)]} </math>
	<math>~=</math>	<math> ~\Chi_\mathrm{ad}^{n-3} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(n-3)(n-1)/[2(n+1)]} \biggl[ \mathcal{A}^{-(n+1)(n-3)} \mathcal{B}^{2n(n-3)} \biggr]^{1/[2(n+1)]} \biggl[ G^{(3-n)(n+1)} K^{2n(n-3)} P_e^{(n-3)(1-n)} \biggr]^{1/[2(n+1)]} </math>
	<math>~=</math>	<math> ~R_\mathrm{SWS}^{n-3} \biggl( \frac{n}{n+1} \biggr)^{(n-3)/2} \Chi_\mathrm{ad}^{n-3} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(n-3)(n-1)/[2(n+1)]} \biggl[ \mathcal{A}^{-(n+1)(n-3)} \mathcal{B}^{2n(n-3)} \biggr]^{1/[2(n+1)]} </math>
<math>~\Rightarrow~~~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } </math>	<math>~=</math>	<math> ~\biggl( \frac{n}{n+1} \biggr)^{1/2} \Chi_\mathrm{ad} \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(n-1)/[2(n+1)]} \biggl[ \frac{\mathcal{B}^{n/(n+1)}}{\mathcal{A}^{1/2}} \biggr] \, . </math>

Flipping both of these expressions around, we see that,

<math>~\Pi_\mathrm{ad} </math>

<math> ~\frac{4\pi}{3} \biggl\{ \biggl( \frac{n+1}{n} \biggr)^{3(n+1)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2(n+1)} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr] \biggr\}^{1/(n-3)} \, , </math>

and,

<math>~\Chi_\mathrm{ad} </math>	<math>~=</math>	<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggl( \frac{n+1}{n} \biggr)^{1/2} \biggl[ \frac{\mathcal{A}^{1/2}}{\mathcal{B}^{n/(n+1)}} \biggr] \biggl( \frac{3\Pi_\mathrm{ad} }{4\pi} \biggr)^{(1-n)/[2(n+1)]} </math>
	<math>~=</math>	<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggl( \frac{n+1}{n} \biggr)^{1/2} \biggl[ \frac{\mathcal{A}^{1/2}}{\mathcal{B}^{n/(n+1)}} \biggr] \biggl\{ \biggl( \frac{n+1}{n} \biggr)^{3(n+1)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2(n+1)} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr] \biggr\}^{(1-n)/[2(n+1)(n-3)]} </math>
	<math>~=</math>	<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{(1-n)/(n-3)} \biggl( \frac{n}{n+1} \biggr)^{n/(n-3)} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \, . </math>

Hence, our earlier derived compact expression for the virial theorem becomes,

<math>~1</math>	<math>~=</math>	<math> \biggl\{ \frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{(1-n)/(n-3)} \biggl( \frac{n}{n+1} \biggr)^{n/(n-3)} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \biggr\}^{(n-3)/n} </math>
		<math> -~ \frac{4\pi}{3} \biggl\{ \biggl( \frac{n+1}{n} \biggr)^{3(n+1)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2(n+1)} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr] \biggr\}^{1/(n-3)} \biggl\{ \frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{(1-n)/(n-3)} \biggl( \frac{n}{n+1} \biggr)^{n/(n-3)} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \biggr\}^4 </math>
	<math>~=</math>	<math> \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggr)^{(n-3)/n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{(1-n)/n} \biggl( \frac{n}{n+1} \biggr) \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr] -~ \frac{4\pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggr)^4 \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{-2} \biggl( \frac{n}{n+1} \biggr) \frac{1}{\mathcal{A}} \, . </math>

Or, rearranged,

<math>\frac{4\pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggr)^4 - \mathcal{B} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS} } \biggr)^{(n-3)/n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} +~ \mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2} = 0 \, . </math>

After adopting modified length- and mass-normalizations, <math>~R_\mathrm{mod}</math> and <math>~M_\mathrm{mod}</math>, such that,

<math>~\frac{M_\mathrm{SWS}}{M_\mathrm{mod}}</math>	<math>~\equiv</math>	<math>~\biggl( \frac{4\pi}{3} \biggr)^{2n/(n+1)} \biggl[ \frac{3(n+1)}{4\pi n} \biggr]^{3/2} \frac{\mathcal{A}^{3/2}}{\mathcal{B}^{2n/(n+1)}} \, ,</math>
<math>~\frac{R_\mathrm{SWS}}{R_\mathrm{mod}}</math>	<math>~\equiv</math>	<math>~\biggl( \frac{4\pi}{3} \biggr)^{n/(n+1)} \biggl[ \frac{3(n+1)}{4\pi n} \biggr]^{1/2} \frac{\mathcal{A}^{1/2}}{\mathcal{B}^{n/(n+1)}} \, ,</math>

we obtain the

Virial Theorem in terms of Mass and Radius

<math> \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{mod}} \biggr)^4 - \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{mod}} \biggr)^{(n-3)/n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{mod}} \biggr)^{(n+1)/n} + \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{mod}} \biggr)^2 = 0 \, . </math>

This analytic function is plotted for seven different values of the polytropic index, <math>~n</math>, as indicated, in the lefthand diagram of the following table.

Now that we have this very general, yet concise, algebraic expression for the mass-radius relationship of all pressure-truncated polytropes, let's replace the new "mod" normalizations with Stahler's original normalizations, <math>~R_\mathrm{SWS}</math> and <math>~M_\mathrm{SWS}</math>, to understand more completely how this general expression should be viewed in relation to the parametric relations provided by solutions of the detailed force-balanced models. We will henceforth use the notation,

<math>~\mathcal{X}</math>	<math>~\equiv</math>	<math>~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \, ,</math>
<math>~\mathcal{Y}</math>	<math>~\equiv</math>	<math>~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \, .</math>

In the virial theorem expression we will make the following replacements:

<math>~\frac{R_\mathrm{eq}}{R_\mathrm{mod}} ~~~ \rightarrow ~~~ \mathcal{X} \cdot \frac{R_\mathrm{SWS}}{R_\mathrm{mod}}</math>	<math>~=</math>	<math>~\mathcal{X} \biggl( \frac{4\pi}{3} \biggr)^{n/(n+1)} \biggl[ \frac{3(n+1)}{4\pi n} \biggr]^{1/2} \frac{\mathcal{A}^{1/2}}{\mathcal{B}^{n/(n+1)}} \, ,</math>
<math>~\frac{M_\mathrm{tot}}{M_\mathrm{mod}} ~~~ \rightarrow ~~~ \mathcal{Y} \cdot \frac{M_\mathrm{SWS}}{M_\mathrm{mod}}</math>	<math>~=</math>	<math>~\mathcal{Y} \biggl( \frac{4\pi}{3} \biggr)^{2n/(n+1)} \biggl[ \frac{3(n+1)}{4\pi n} \biggr]^{3/2} \frac{\mathcal{A}^{3/2}}{\mathcal{B}^{2n/(n+1)}} \, . </math>

Next, we recognize that, in order to graphically display the mass-radius relation derived from the virial theorem in the <math>~\mathcal{X}-\mathcal{Y}</math> plane, we must write out the expressions for the free-energy coefficients. After setting <math>~M_\mathrm{limit}/M_\mathrm{tot} = 1</math> in the above summary expressions, we obtain,

<math>~\mathcal{A}</math>	<math>~=</math>	<math>\frac{1}{5} \cdot \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} = \frac{1}{5-n} \, ,</math>
<math>~\mathcal{B}</math>	<math>~\equiv</math>	<math> \biggl( \frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{(n+1)/n}} = \frac{1}{3(5-n) ( 4\pi )^{1/n}} \biggl[ 3(n+1) (\tilde\theta^')^2 + (5-n)\tilde\theta^{n+1} \biggr] \biggl( \frac{\tilde\xi}{\tilde\theta^'} \biggr)^{(n+1)/n} \, . </math>

In an effort not to be caught dividing by zero while investigating the specific case of <math>~n=5</math> polytropes, we will adopt as shorthand notation,

<math>\mathfrak{b}_n \equiv \biggl[ (4\pi)^{1/n} (5-n)\mathcal{B}\biggr] = \biggl[ (n+1) (\tilde\theta^')^2 + \biggl( \frac{5-n}{3} \biggr)\tilde\theta^{n+1} \biggr] \biggl( \frac{\tilde\xi}{\tilde\theta^'} \biggr)^{(n+1)/n} \, . </math>

Hence, the replacements become,

<math>~\frac{R_\mathrm{eq}}{R_\mathrm{mod}} </math>	<math>~~~ \rightarrow ~~~</math>	<math>~\mathcal{X} \biggl( \frac{4\pi}{3} \biggr)^{n/(n+1)} \biggl[ \frac{3(n+1)}{4\pi n} \biggr]^{1/2} (5-n)^{(n-1)/[2(n+1)]} (4\pi)^{1/(n+1)} \mathfrak{b}_n^{-n/(n+1)} </math>
	<math>~=</math>	<math>~\mathcal{X} (5-n)^{(n-1)/[2(n+1)]} \biggl( \frac{n+1}{n} \biggr)^{1/2} (4\pi)^{1/2} \cdot 3^{(1-n)/[2(n+1)]} \cdot \mathfrak{b}_n^{-n/(n+1)} \, , </math>
<math>~\frac{M_\mathrm{tot}}{M_\mathrm{mod}} </math>	<math>~~~ \rightarrow ~~~</math>	<math>~\mathcal{Y} \biggl( \frac{4\pi}{3} \biggr)^{2n/(n+1)} \biggl[ \frac{3(n+1)}{4\pi n} \biggr]^{3/2} (5-n)^{(n-3)/[2(n+1)]} (4\pi)^{2/(n+1)} \mathfrak{b}_n^{-2n/(n+1)} </math>
	<math>~=</math>	<math>~\mathcal{Y} (5-n)^{(n-3)/[2(n+1)]} \biggl( \frac{n+1}{n} \biggr)^{3/2} (4\pi)^{1/2} \cdot 3^{(3-n)/[2(n+1)]} \cdot \mathfrak{b}_n^{-2n/(n+1)} \, , </math>

and, in particular, the cross term in the virial theorem expression becomes,

<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{mod}} \biggr)^{(n-3)/n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{mod}} \biggr)^{(n+1)/n}</math>

<math>~\mathcal{X}^{(n-3)/n} \mathcal{Y}^{(n+1)/n} \biggl( \frac{5-n}{3} \biggr)^{(n-3)/(n+1)} \biggl( \frac{n+1}{n} \biggr)^{2} (4\pi)^{(n-1)/n} \cdot \mathfrak{b}_n^{(1-3n)/(n+1)} \, . </math>

Via these replacements the concise and general Virial Theorem expression derived above morphs into the,

Virial Theorem written in terms of <math>~\mathcal{X}</math>, <math>~\mathcal{Y}</math>, and <math>~\mathfrak{b}_n</math>

<math> k_\xi \biggl\{ \mathcal{X}^4 \biggl[\frac{4\pi (5-n)}{3} \biggr] - \mathcal{X}^{(n-3)/n} \mathcal{Y}^{(n+1)/n} (4\pi)^{-1/n} \mathfrak{b}_n + \mathcal{Y}^2 \biggl(\frac{n+1}{n}\biggr) \biggr\} = 0 \, , </math>

where the leading coefficient is,

<math>~\equiv</math>

<math>~ 4\pi \biggl( \frac{5-n}{3} \biggr)^{(n-3)/(n+1)} \biggl(\frac{n+1}{n} \biggr)^2 \mathfrak{b}_n^{-4n/(n+1)} \, . </math>

In carrying out this last derivation we could be accused of reinventing the wheel, as the expression inside the curly braces is simply <math>~(5-n)</math> times the virial expression presented inside an outlined box, above, just before we introduced the modified normalization parameters, <math>~R_\mathrm{mod}</math> and <math>~M_\mathrm{mod}</math>.

Relating and Reconciling Two Mass-Radius Relationships for n = 5 Polytropes

Now, let's examine the case of pressure-truncated, <math>~n=5</math> polytropes. As we have discussed in the context of detailed force-balanced models, Stahler (1983) has deduced that all <math>~n=5</math> equilibrium configurations obey the mass-radius relationship,

<math>~\biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^2 - 5 \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) + \frac{2^2 \cdot 5 \pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 </math>

where, as reviewed above, the mass and radius normalizations, <math>~M_\mathrm{SWS}</math> and <math>~R_\mathrm{SWS}</math>, may be treated as constants once the parameters <math>~K</math> and <math>~P_e</math> are specified. In contrast to this, the mass-radius relationship that we have just derived from the virial theorem for pressure-truncated, <math>~n=5</math> polytropes is,

<math> \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{mod}} \biggr)^2 - \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{mod}} \biggr)^{2/5} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{mod}} \biggr)^{6/5} + \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{mod}} \biggr)^4 = 0 \, , </math>

where the mass and radius normalizations,

<math>~M_\mathrm{mod}\biggr\|_{n=5}</math>	<math>~=</math>	<math>~M_\mathrm{SWS} \biggl( \frac{3\mathcal{B}}{4\pi} \biggr)^{5/3} \biggl[ \frac{2\cdot 5\pi}{3^2 \mathcal{A}} \biggr]^{3/2} \, ,</math>
<math>~R_\mathrm{mod}\biggr\|_{n=5}</math>	<math>~=</math>	<math>~R_\mathrm{SWS} \biggl( \frac{3\mathcal{B}}{4\pi}\biggr)^{5/6} \biggl[ \frac{2\cdot 5\pi}{3^2\mathcal{A}} \biggr]^{1/2} \, ,</math>

depend, not only on <math>~K</math> and <math>~P_e</math> via the definitions of <math>~M_\mathrm{SWS}</math> and <math>~R_\mathrm{SWS}</math>, but also on the structural form factors via the free-energy coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. While these two separate mass-radius relationships are similar, they are not identical. In particular, the middle term involving the cross-product of the mass and radius contains different exponents in the two expressions. It is not immediately obvious how the two different polynomial expressions can be used to describe the same physical sequence.

This apparent discrepancy is reconciled as follows: The structural form factors — and, hence, the free-energy coefficients — vary from equilibrium configuration to equilibrium configuration. So it does not make sense to discuss evolution along the sequence that is defined by the second of the two polynomial expressions. If you want to know how a given system's equilibrium radius will change as its mass changes, the first of the two polynomials will do the trick. However, the equilibrium radius of a given system can be found by looking for extrema in the free-energy function while holding the free-energy coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, constant; more importantly, the relative stability of a given equilibrium system can be determined by analyzing the behavior of the system's free energy while holding the free-energy coefficients constant. Dynamically stable versus dynamically unstable configurations can be readily distinguished from one another along the sequence that is defined by the second polynomial expression; they cannot be readily distinguished from one another along the sequence that is defined by the first polynomial expression. It is useful, therefore, to determine how to map a configuration's position on one of the sequences to the other.

Plotting Stahler's Relation

Switching, again, to the shorthand notation,

<math>~\mathcal{X}</math>	<math>~\equiv</math>	<math>~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \, ,</math>
<math>~\mathcal{Y}</math>	<math>~\equiv</math>	<math>~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \, ,</math>

the equilibrium mass-radius relation defined by the first of the two polynomial expressions can be plotted straightforwardly in either of two ways. One way is to recognize that the polynomial is a quadratic expression whose solution is,

<math>~\mathcal{Y}</math>

<math>~\frac{5}{2} \mathcal{X} \biggl\{ 1 \pm \biggl[ 1 - \biggl( \frac{2^4\cdot \pi}{3\cdot 5^2} \biggr) \mathcal{X}^2 \biggr]^{1/2} \biggr\} \, .</math>

Another is to determine the normalized mass and normalized radius individually through Stahler's pair of parametric relations. Drawing partly from our above discussion and partly from a separate discussion where we provide a tabular summary of the properties of pressure-truncated <math>~n=5</math> polytropes, these are,

<math> ~\mathcal{X}\biggr\|_{n=5} </math>	<math>~=~</math>	<math> \biggl( \frac{5}{4\pi} \biggr)^{1/2} \tilde\xi \tilde\theta^{2} = \biggl\{ \frac{3\cdot 5}{2^2 \pi} \biggl[ \frac{\tilde\xi^2/3}{(1+\tilde\xi^2/3)^{2}} \biggr] \biggr\}^{1/2} \, , </math>
<math> ~\mathcal{Y}\biggr\|_{n=5} </math>	<math>~=~</math>	<math> \biggl( \frac{5^3}{4\pi} \biggr)^{1/2} \tilde\theta (- \tilde\xi^2 \tilde\theta^') = \biggl[ \biggl( \frac{3 \cdot 5^3}{2^2\pi} \biggr) \frac{(\tilde\xi^2/3)^3}{(1+\tilde\xi^2/3)^{4}} \biggr]^{1/2} \, . </math>

The entire sequence will be traversed by varying the Lane-Emden parameter, <math>~\tilde\xi</math>, from zero to infinity. In each of the figure panels presented below, Stahler's mass-radius relation has been plotted using the solution to the quadratic equation; points along the sequence derived from the positive root are shown in green while those derived from the negative root are shown in blue. But also in each panel, the pair of parametric equations has been used to identify the specific equilibrium configuration that corresponds to a particular choice of <math>~\tilde\xi</math>, as indicated.

Plotting the Virial Theorem Relation

The relevant relation is obtained by plugging <math>~n = 5</math> into the general mass-radius relation derived above, repeated here for clarity:

<math> \mathcal{X}^4 \biggl[\frac{4\pi (5-n)}{3} \biggr] - \mathcal{X}^{(n-3)/n} \mathcal{Y}^{(n+1)/n} (4\pi)^{-1/n} \mathfrak{b}_\pi + \mathcal{Y}^2 \biggl(\frac{n+1}{n}\biggr) = 0 </math>

where,

<math>\mathfrak{b}_n = \biggl[ (n+1) (-\tilde\theta^')^2 + \biggl( \frac{5-n}{3} \biggr)\tilde\theta^{n+1} \biggr] \biggl( \frac{\tilde\xi}{-\tilde\theta^'} \biggr)^{(n+1)/n} </math>

We obtain,

<math>~\mathcal{Y}^2 \biggl(\frac{6}{5}\biggr) </math>	<math>~=</math>	<math>\mathcal{X}^{2/5} \mathcal{Y}^{6/5} (4\pi)^{-1/5} \mathfrak{b}_{n=5} </math>
<math>~\Rightarrow ~~~~ \mathcal{Y}^4 </math>	<math>~=</math>	<math>\mathcal{X}^{2} \biggl[ \biggl( \frac{5^5}{2^5\cdot 3^5}\biggr) \frac{\mathfrak{b}^5_{n=5}}{4\pi} \biggr] = \mathcal{X}^{2} \biggl( \frac{5^5}{4\pi}\biggr) \biggl[ (-\tilde\theta^')^{4} \tilde\xi^6 \biggr]_{n=5} </math>
<math>~\Rightarrow ~~~~ \mathcal{Y}^2 </math>	<math>~=</math>	<math> \mathcal{X} \biggl( \frac{5^5}{2^2 \cdot 3^4 \pi}\biggr)^{1/2} \biggl[ \tilde\xi^{5} \biggl( 1 + \frac{\tilde\xi^2}{3} \biggr)^{-3} \biggr] \, . </math>

In order to arrive at this last expression, we have inserted the definition of <math>~\tilde\theta^'</math> as provided for <math>~n=5</math> polytropic structures in another section's summary table. It is worth emphasizing that, for this particular case, the final polynomial expression is relatively simple because one term in the virial expression and another in the definition of <math>~\mathfrak{b}_n</math> that included the coefficient, <math>~(5-n)</math>, were set to zero.

Relating and Reconciling Two Mass-Radius Relationships for n = 4 Polytropes

User:Tohline/SSC/Virial/PolytropesSummary

Contents

Virial Equilibrium of Adiabatic Spheres (Summary)

Detailed Force-Balanced Solution

Free Energy Function and Virial Theorem

Relationship to Detailed Force-Balanced Models

Structural Form Factors

Physical Meaning of Parameter <math>~\eta_\mathrm{ad}</math>

Desired Pressure-Radius Relation

Discussion

Model Sequences

When <math>~\eta_\mathrm{ad}</math> is zero

Stability

Try Polytropic Index of 4

Groundwork

First Table

Second Table

Summary

Curiosity

Mass-Radius Relation

Detailed Force-Balanced Solution

Mapping from Above Discussion

Relating and Reconciling Two Mass-Radius Relationships for n = 5 Polytropes

Plotting Stahler's Relation

Plotting the Virial Theorem Relation

Relating and Reconciling Two Mass-Radius Relationships for n = 4 Polytropes

Navigation menu

Search