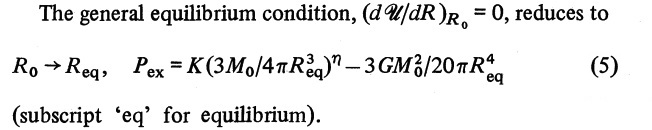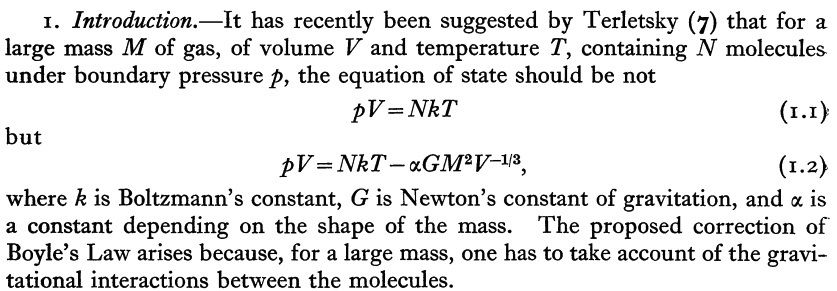Virial Equilibrium

Free Energy Expression (review)

As has been explained elsewhere, associated with any self-gravitating, gaseous configuration we can identify a total "Gibbs-like" free energy, <math>\mathfrak{G}</math>, given by the sum of the relevant contributions to the total energy of the configuration,

<math> \mathfrak{G} = W + U + T_\mathrm{rot} + P_e V + \cdots \, , </math>

where, for the purposes of this discussion, we have explicitly included the gravitational potential energy, <math>W</math>, the total internal energy, <math>U</math>, the rotational kinetic energy, <math>T_\mathrm{rot}</math>, and a term that accounts for surface effects if the configuration of volume <math>V</math> is embedded in an external medium of pressure <math>P_e</math>. For spherically symmetric configurations that have a uniform density and are uniformly rotating, each of the terms contributing to this free-energy expression can be written as a product of a scalar coefficient and a function of the configuration's radius, <math>R</math>, as follows:

<math> \mathfrak{G} = -A\biggl( \frac{R}{R_0} \biggr)^{-1} +~ (1-\delta_{1\gamma_g})B\biggl( \frac{R}{R_0} \biggr)^{-3(\gamma_g-1)} -~ \delta_{1\gamma_g} B_I \ln \biggl( \frac{R}{R_0} \biggr) +~ C \biggl( \frac{R}{R_0} \biggr)^{-2} +~ D\biggl( \frac{R}{R_0} \biggr)^3 \, , </math>

where, <math>R_0</math> is an, as yet unspecified, scale length,

<math>A</math>	<math>\equiv</math>	<math>\frac{3}{5} \frac{GM^2}{R_0} \, ,</math>
<math>B</math>	<math>\equiv</math>	<math> \biggl[ \frac{K}{(\gamma_g-1)} \biggl( \frac{3}{4\pi R_0^3} \biggr)^{\gamma_g - 1} \biggr] M^{\gamma_g} \, , </math>
<math>B_I</math>	<math>\equiv</math>	<math> 3c_s^2 M =3 KM \, , </math>
<math>C</math>	<math>\equiv</math>	<math> \frac{5J^2}{4MR_0^2} \, , </math>
<math>D</math>	<math>\equiv</math>	<math> \frac{4}{3} \pi R_0^3 P_e \, . </math>

As written here, the coefficient <math>B</math> that appears in the definition of the configuration's total internal energy comes from assuming that the configuration will expand or contract adiabatically, that is, that internally the pressure scales with density as,

<math>P = K \rho^{\gamma_g} \, ,</math>

where <math>K</math> specifies the specific entropy of the gas and <math>~\gamma_\mathrm{g}</math> <math>\ne 1</math> is the ratio of specific heats. (Note that the Kroniker delta function <math>\delta_{1\gamma_g} = 0</math>, since <math>\gamma_g \ne 1</math>.) If compressions/expansions occur isothermally (<math>\gamma_g = 1</math>, hence, <math>\delta_{1\gamma_g} = 1</math>), the relevant <math>P-\rho</math> relationship is,

Once the pressure exerted by the external medium (<math>P_e</math>), and the configuration's mass (<math>M</math>), angular momentum (<math>J</math>), and specific entropy (via <math>K</math>) — or, in the isothermal case, sound speed (<math>c_s</math>) — have been specified, the values of all of the coefficients are known and this algebraic expression for <math>\mathfrak{G}</math> describes how the free energy of the configuration will vary with the configuration's size (<math>R</math>) for a given choice of <math>\gamma_g</math>.

Visual Representation

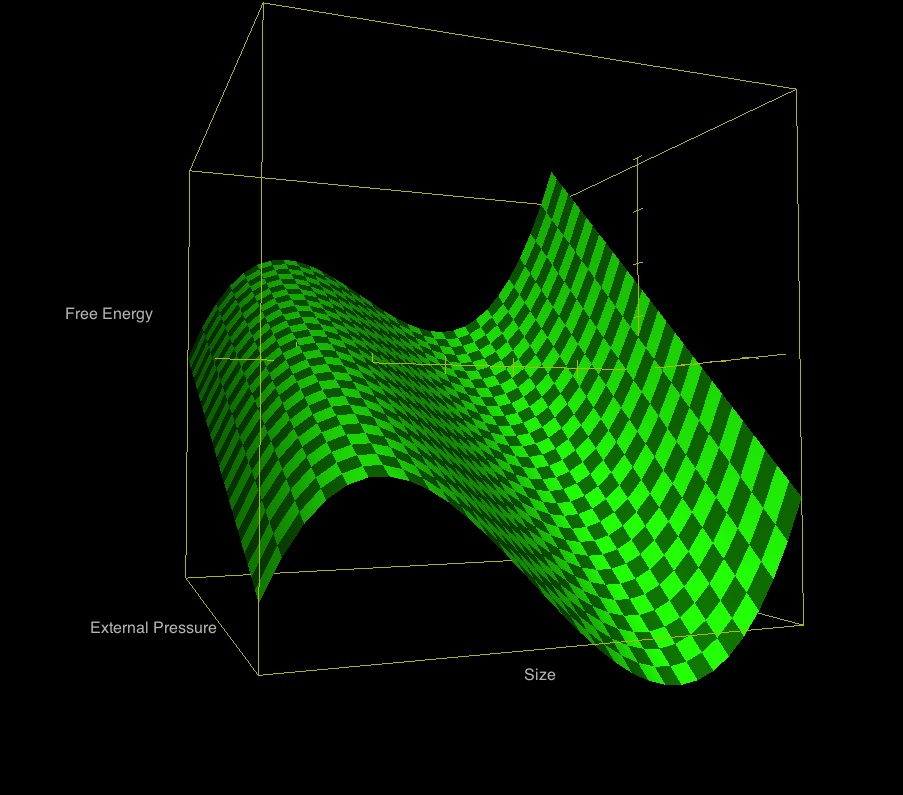
Figure 1: Free Energy Surface

This segment of the free energy "surface" shows how the free energy varies as the size of the configuration and the applied external pressure are varied, while all other relevant physical attributes are held fixed.

The plotted function — derived from the above expression for <math>\mathfrak{G}</math>, with <math>\gamma_\mathrm{g} = 1</math> and <math>C=0</math> (see further discussion, below) — is, specifically,

<math> \frac{\mathfrak{G}}{3Mc_s^2} = 3000\biggl[ - \frac{1}{\chi} - \ln\chi + \frac{\Pi}{3}\chi^3 + 0.9558 \biggr] \, . </math>

As shown, the size of the configuration <math>(\chi)</math> increases to the right from <math>1.2</math> to <math>1.51</math>; the dimensionless external pressure <math>(\Pi)</math> increases into the screen from <math>0.103</math> to <math>0.104</math>; and the dimensionless free energy, <math>\mathfrak{G}/(3Mc_s^2)</math>, increases upward.

Energy Extrema

As is illustrated in Figure 1, above, the free energy "surface" generally will exhibit multiple local minima and local maxima, and may also possess one or more points of inflection. The locations along the energy surface where these special points arise identify equilibrium states, and the associated values of <math>(R/R_0)_\mathrm{eq}</math> give the radii of the equilibrium configurations.

For a given choice of the set of physical parameters <math>M</math>, <math>K</math>, <math>J</math>, <math>P_e</math>, and <math>\gamma_g</math>, extrema occur wherever,

<math> \frac{d\mathfrak{G}}{dR} = 0 \, . </math>

For the free energy function identified above,

<math> \frac{d\mathfrak{G}}{dR} = \frac{1}{R_0} \biggl[ A\chi^{-2} +~ (1-\delta_{1\gamma_g})~3(1 - \gamma_g) B\chi^{2 -3\gamma_g} -~ \delta_{1\gamma_g} B_I \chi^{-1} ~ -2C \chi^{-3} +~ 3D\chi^2 \biggr] \, . </math>

where,

<math>\chi \equiv \frac{R}{R_0} \, .</math>

So <math>\chi_\mathrm{eq} \equiv (R/R_0)_\mathrm{eq}</math> is obtained from the real root(s) of the equation,

<math> A \chi^{-2} +~ (1-\delta_{1\gamma_g})~3(1 - \gamma_g) B\chi^{2 -3\gamma_g} -~ \delta_{1\gamma_g} B_I \chi^{-1} ~ -2C \chi^{-3} +~ 3D\chi^2 = 0 \, , </math>

or, equivalently, from the roots of the equation,

<math> 2C \chi^{-2} + ~ (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>

As a definition of equilibrium states, this last expression is also the well-known scalar virial equation, derivable from the first moment of the equation of motion. A more recognizable expression can be obtained by replacing each of the terms by the energy contents that they represent:

<math> 2(T_\mathrm{rot} + S) + W - 3P_e V = 0 \, . </math>

In this expression, <math>S</math> is the thermal energy content of the configuration; the relationship between <math>S</math> and the configuration's total internal energy, <math>U</math>, is provided in our associated derivation of both the adiabatic and isothermal free energy functions.

Examples

Isolated, Nonrotating Configuration

For a nonrotating configuration <math>(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>(D=P_e = 0)</math>, the statement of virial equilibrium is,

<math> (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} = 0 \, . </math>

Isothermal

For isothermal configurations <math>(\delta_{1\gamma_g} = 1)</math>, one and only one equilibrium state arises where,

that is,

<math> R_\mathrm{eq} = R_0 \chi_\mathrm{eq} = \frac{A}{B_I}\cdot R_0 = \frac{GM}{5c_s^2} \, . </math>

Adiabatic

For adiabatic configurations <math>(\delta_{1\gamma_g} = 0)</math>, one equilibrium state exists for each value of <math>\gamma_g</math> and it occurs where,

<math> 3(\gamma_g-1) B\chi^{3 -3\gamma_g} = A\chi^{-1} \, , </math>

that is, where,

<math> R_\mathrm{eq} = R_0 \chi_\mathrm{eq} = \biggl[ \frac{3(\gamma_g-1) B}{A} \cdot R_0^{(3\gamma_g-4)} \biggr]^{1/(3\gamma_g-4)} = \biggl[ 5\biggl( \frac{3}{4\pi} \biggr)^{\gamma_g-1} \cdot \frac{KM^{(\gamma_g-2)}}{G} \biggr]^{1/(3\gamma_g-4)} \, . </math>

Notice that, for <math>\gamma_g=2</math>, the equilibrium radius depends only on the specific entropy of the gas and is independent of the configuration's mass. Conversely, notice that, for <math>\gamma_g = 4/3</math>, the mass of the configuration is independent of the radius. For all other values of <math>\gamma_g</math>, the equilibrium mass-radius relationship for adiabatic configurations is,

<math> M^{(\gamma_g - 2)} \propto R_\mathrm{eq}^{(3\gamma_g -4)} \, . </math>

This means that, for <math>\gamma_g</math> > <math> 2</math> or <math>\gamma_g </math>< <math>4/3</math>, configurations with larger mass (but the same specific entropy) have larger equilibrium radii. However, for <math>\gamma_g</math> in the range, <math>2</math> > <math>\gamma_g </math> > <math>4/3</math>, configurations with larger mass have smaller equilibrium radii.

Note that the result obtained for the isothermal configuration could have been obtained by setting <math>\gamma_g = 1</math> in this adiabatic solution, because <math>K = c_s^2</math> when <math>\gamma_g = 1</math>.

Nonrotating Configuration Embedded in an External Medium

For a nonrotating configuration <math>(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>P_e</math> of, an external medium, the statement of virial equilibrium is,

<math> (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>

Adiabatic

Hence, for adiabatic configurations <math>(\delta_{1\gamma_g} = 0)</math>, equilibrium states exist at radii given by the roots of the following expression:

<math> 3(\gamma_g-1) B\chi^{3 -3\gamma_g} ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>

This is precisely the same condition that derives from setting equation (3) to zero in Whitworth's (1981, MNRAS, 195, 967) discussion of the "global gravitational stability for one-dimensional polyropes." The overlap with Whitworth's narative is perhaps clearer after introducing the algebraic expressions for the coefficients <math>A</math>, <math>B</math>, and <math>D</math>, dividing the equation through by <math>(3\chi^3 V_0) = (4\pi R^3)</math>, and rewriting <math>R</math> as <math>R_\mathrm{eq}</math> to obtain,

<math> P_e = K \biggl( \frac{3M}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} - \biggl( \frac{3GM^2}{20\pi R_\mathrm{eq}^4} \biggr) \, . </math>

This exactly matches equation (5) of Whitworth, which reads:

Ideally we would like to invert this equation to obtain an analytic expression for the configuration's equilibrium radius in terms of the physical parameters, <math>M</math>, <math>K</math>, and <math>P_e</math>. However, this cannot be accomplished for an arbitrary value of the adiabatic exponent, <math>\gamma_g</math>.

Isothermal

For isothermal configurations <math>(\delta_{1\gamma_g} = 1)</math>, we deduce that equilibrium states exist at radii given by the roots of the equation,

Bonnor's (1956) Equivalent Relation

Inserting the expressions for the coefficients <math>B_I</math>, <math>A</math>, and <math>D</math> gives,

<math> 3Mc_s^2 ~- \frac{3}{5} \frac{GM^2}{R} = 3 P_e \biggl( \frac{4\pi}{3} R^3\biggr) \, , </math>

or, because the volume <math>V = (4\pi R^3/3)</math> for a spherical configuration, we can write,

<math> 3P_e V = 3Mc_s^2 ~- \frac{3}{5} \biggl( \frac{4\pi}{3} \biggr)^{1/3} \frac{GM^2}{V^{1/3}} \, . </math>

It is instructive to compare this expression for a self-gravitating, isothermal equilibrium sphere to the one that was presented in 1956 by Bonnor (1956, MNRAS, 116, 351) as equation (1.2) in a paper titled, "Boyle's Law and Gravitational Instability":

Once we realize that, for an isothermal configuration, twice the thermal energy content, <math>2S</math>, can be written as <math>(3NkT)</math> just as well as via the product, <math>(3Mc_s^2)</math>, we see that our expression is identical to Bonnor's if we set the prefactor on Bonnor's last term, <math>\alpha = (4\pi/3)^{1/3}/5</math>. (Indeed, later on the first page of his paper, Bonnor points out that this is the appropriate value for <math>\alpha</math> when considering a uniform density sphere.)

P-V Diagram

Returning to the dimensionless form of this expression and multiplying through by <math>[-\chi/(3D)]</math>, we obtain,

Now, taking a cue from the solution presented above for an isolated isothermal configuration, we choose to set the previously unspecified scale factor, <math>R_0</math>, to,

in which case <math>B_I = A</math>, and the quartic equation governing the radii of equilibrium states becomes, simply,

where,

<math> \Pi \equiv \frac{3D}{B_I} = \frac{4\pi R_0^3 P_e}{3Mc_s^2} = \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 c_s^8} \, . </math>

For a given choice of configuration mass and sound speed, this parameter, <math>\Pi</math>, can be viewed as a dimensionless external pressure. Alternatively, for a given choice of <math>P_e</math> and <math>c_s</math>, <math>\Pi^{1/2}</math> can represent a dimensionless mass; or, for a given choice of <math>M</math> and <math>P_e</math>, <math>\Pi^{-1/8}</math> can represent a dimensionless sound speed. Here we will view it as a dimensionless external pressure.

The above quartic equation can be rearranged immediately to give the external pressure that is required to obtain a particular configuration radius, namely,

Quartic Solution

Equilibrium configurations may be found at the four roots of this quartic equation, assuming the roots are real.

Roots of the quartic equation: <math>\chi^4 - \chi \Pi^{-1}+ \Pi^{-1} = 0 </math>

<math>\chi_1</math>	<math>=</math>	<math> +\frac{1}{2} y_r^{1/2} + \frac{1}{2} D_q \, ; </math>
<math>\chi_2</math>	<math>=</math>	<math> +\frac{1}{2} y_r^{1/2} - \frac{1}{2} D_q \, ; </math>
<math>\chi_3</math>	<math>=</math>	<math> -\frac{1}{2} y_r^{1/2} + \frac{1}{2} E_q \, ; </math>
<math>\chi_4</math>	<math>=</math>	<math> -\frac{1}{2} y_r^{1/2} - \frac{1}{2} E_q \, , </math>

where,

<math>D_q</math>	<math>\equiv</math>	<math> y_r^{1/2} \biggl[ \frac{2}{\Pi} y_r^{-3/2} - 1 \biggr]^{1/2} \, , </math>
<math>E_q</math>	<math>\equiv</math>	<math> y_r^{1/2} \biggl[ - \frac{2}{\Pi} y_r^{-3/2} - 1 \biggr]^{1/2} \, , </math>

and,

<math> y_r \equiv \biggl( \frac{1}{2\Pi^2} \biggr)^{1/3} \biggl\{ \biggl[ 1 + \sqrt{1-\frac{2^8}{3^3}\Pi} \biggr]^{1/3} + \biggl[ 1 - \sqrt{1-\frac{2^8}{3^3}\Pi} \biggr]^{1/3} \biggr\} \, , </math>

is the real root of the cubic equation,

Show that derived result is, essentially, the Bonnor-Ebert sphere. Should we also draw analogy with collapse of isothermal core of red giant, or leave this to the later stability discussion?

User:Tohline/SphericallySymmetricConfigurations/Virial

Contents

Virial Equilibrium

Free Energy Expression (review)

Visual Representation

Energy Extrema

Examples

Isolated, Nonrotating Configuration

Isothermal

Adiabatic

Nonrotating Configuration Embedded in an External Medium

Adiabatic

Isothermal

Bonnor's (1956) Equivalent Relation

P-V Diagram

Quartic Solution

Navigation menu

Search