Toroidal Configurations and Related Coordinate Systems

Preamble

As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?

I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.¹ (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.

I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened, axisymmetric potentials.^2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system.

Toroidal Coordinates

Presentation by MF53

The orthogonal toroidal coordinate system <math>(\xi_1,\xi_2,\xi_3=\cos\varphi)</math> discussed by MF53 has the following properties:

<math> \frac{x}{a} </math>	<math> = </math>	<math> \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\cos\varphi </math>
<math> \frac{y}{a} </math>	<math> = </math>	<math> \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\sin\varphi </math>
<math> \frac{z}{a} </math>	<math> = </math>	<math> \frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} </math>
<math> \frac{\varpi}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 \biggr]^{1/2} </math>	<math> = </math>	<math> \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} </math>
<math> \frac{r}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 + \biggl(\frac{z}{a}\biggr)^2\biggr]^{1/2} </math>	<math> = </math>	<math> \biggl[ \frac{\xi_1 + \xi_2}{\xi_1 - \xi_2} \biggr]^{1/2} </math>

According to MF53, the associated scale factors of this orthogonal coordinate system are:

<math> \frac{h_1}{a} </math>	<math> = </math>	<math> \frac{1}{(\xi_1 - \xi_2)(\xi_1^2 - 1)^{1/2}} </math>
<math> \frac{h_2}{a} </math>	<math> = </math>	<math> \frac{1}{(\xi_1 - \xi_2)(1-\xi_2^2)^{1/2}} </math>
<math> \frac{h_3}{a} </math>	<math> = </math>	<math> \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\frac{1}{\sin\varphi} </math>

Tohline's Ramblings

My inversion of these coordinate definitions has lead to the following expressions:

<math> \xi_1 </math>	<math> = </math>	<math> \frac{r(r^2 + 1)} {[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} </math>
<math> \xi_2 </math>	<math> = </math>	<math> \frac{r(r^2 - 1)}{[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} </math>

where,

<math> \chi \equiv \frac{\varpi}{a} ~~~;~~~\zeta\equiv\frac{z}{a} ~~~\mathrm{and} ~~~ r=(\chi^2 + \zeta^2)^{1/2} . </math>

Apparently the allowed ranges of the two meridional-plane coordinates are:

<math> +1 \leq \xi_1 \leq \infty ~~~\mathrm{and} ~~~ -1 \leq \xi_2 \leq +1 . </math>

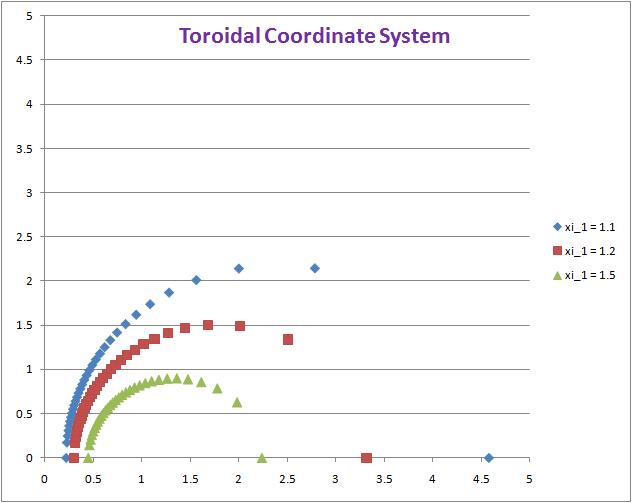
Example Toroidal Surfaces

$Meridional contours of constant <math>\xi_1</math>.$

In the accompanying figure, we've outlined three different a <math>\xi_1 = \mathrm{constant}</math> meridional contours for the MF53 toroidal coordinate system. The illustrated values are,

<math> \xi_1 </math>	=	1.1	(blue);
<math> \xi_1 </math>	=	1.2	(red);
<math> \xi_1 </math>	=	1.5	(gold);

References

Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

User:Tohline/Appendix/Ramblings/ToroidalCoordinates

Contents