User:Tohline/Apps/Wong1973Potential
Wong's (1973) Analytic Potential

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Drawing principally from the published works of C.-Y. Wong (1973, Annals of Physics, 77, 279) and H. S. Cohl & J. E. Tohline (1999, ApJ, 527, 86), in an accompanying discussion we have detailed how the gravitational potential of any finite mass distribution can be determined using toroidal coordinates, rather than, say, cartesian, spherical or cylindrical coordinates. Specifically for axisymmetric systems, the relevant expression derived by Wong (1973) — involving a pair of integrals over the meridional-plane coordinates, <math>~(\eta,\theta)</math>, and a summation over all polar angle modes — is,
|
<math>~\Phi(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2Ga^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \int d\eta^' ~\sinh\eta^'~P^0_{n-1 / 2}(\cosh\eta_<) ~Q^0_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl\{ \frac{ ~\cos[n(\theta - \theta^')]}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr\} \rho(\eta^',\theta^') \, , </math> |
|
Wong (1973), p. 293, Eq. (2.55) |
||
while the expression derived by Cohl & Tohline (1999) — involving different integrand expressions and no summation — is,
|
<math>~\Phi(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2Ga^2 \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{- 1 / 2}(\Chi) \rho(\eta^',\theta^') \, , </math> |
|
Cohl & Tohline (1999), p. 88, Eqs. (31) & (32a) |
||
where, <math>~a</math> is the radius of the toroidal-coordinate system's anchor ring, <math>~P^0_{n-\frac{1}{2}}</math> and <math>~Q^0_{n-\frac{1}{2}}</math> are zero-order half-integer-degree associated Legendre functions of, respectively, the first and second kind, and
|
<math>~\Chi</math> |
<math>~\equiv</math> |
<math>~ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^'} \, . </math> |
In the subsection of our accompanying discussion titled, "Rearranging Terms and Incorporating Special-Function Relations," we have explicitly demonstrated that these two expressions lead to identical evaluations of the gravitational potential.
Here we build upon this technical foundation and detail how Wong (1973) was able to complete both integrals to derive an analytic expression for the potential (inside as well as outside) of axisymmetric, uniform-density tori having an arbitrarily specified ratio of the major to minor (cross-sectional) radii, <math>~R/d</math>. This is an outstanding accomplishment that has received little attention in the astrophysics literature and, therefore, is underappreciated.
Uniform-Density Torus
From an accompanying review, we see that for a torus of major radius <math>~R</math> and minor radius <math>~d</math>, the most accommodating (cylindrical-coordinate-based) radial coordinate location of the toroidal coordinate system's anchor ring is defined such that,
|
<math>~a^2</math> |
<math>~\equiv</math> |
<math>~R^2 - d^2 \, .</math> |
|
Wong (1973), Eq. (2.8) |
||
Then the corresponding (toroidal-coordinate-based) radial coordinate location <math>~\eta_0</math> of the surface of the torus is,
|
<math>~\eta_0</math> |
<math>~=</math> |
<math>~\cosh^{-1}\biggl(\frac{R}{d}\biggr) \, .</math> |
|
Wong (1973), Eq. (2.9) |
||
Alternatively, given <math>~\eta_0</math> and the value of the parameter <math>~a</math>, we have,
|
<math>~R</math> |
<math>~=</math> |
<math>~a \coth\eta_0 \, ,</math> |
|
<math>~d</math> |
<math>~=</math> |
<math>~\frac{a}{\sinh\eta_0} \, .</math> |
|
Wong (1973), Eqs. (2.10) & (2.11) |
||
If such an axisymmetric torus has a uniform density, <math>~\rho_0</math>, then according to the above-cited Cohl & Tohline (1999) expression, the gravitational potential is,
|
<math>~\Phi_\mathrm{CT}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2G\rho_0 a^2 \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \int_{\eta_0}^\infty d\eta^' \int_{-\pi}^\pi d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{- 1 / 2}(\Chi) \, . </math> |
In contrast, according to Wong's (1973) expression, the gravitational potential is,
|
<math>~\Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2G \rho_0 a^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \int_{\eta_0}^\infty d\eta^' ~\sinh\eta^'~P_{n-1 / 2}(\cosh\eta_<) ~Q_{n-1 / 2}(\cosh\eta_>) \int_{-\pi}^\pi \frac{ \cos[n(\theta - \theta^')] d\theta^' }{(\cosh\eta^' - \cos\theta^')^{5/2}} \, . </math> |
|
Wong (1973), p. 293, Eq. (2.55) |
||
Which Is Easier to Evaluate?
As has already been alluded to, upon evaluation, we should expect the expressions for <math>~\Phi_\mathrm{CT}</math> and for <math>~\Phi_\mathrm{W}</math> to give identical values for the gravitational potential at all coordinate locations <math>~(\eta,\theta)</math> across the entire meridional plane. But which of the two expressions is easier to evaluate?
CT
If the desire is to perform the evaluation numerically, then the <math>~\Phi_\mathrm{CT}</math> expression is almost certainly easier to contend with. It only requires a double integration; and as has been detailed in an accompanying discussion, the only relatively unfamiliar special function that appears in the integrand, <math>~Q_{-\frac{1}{2}}(\Chi)</math>, can be re-expressed in terms of (the more familiar) complete elliptic integral of the first kind, namely,
|
<math>~Q_{-\frac{1}{2}}(\Chi)</math> |
<math>~=</math> |
<math>~ \mu K(\mu) \, , </math> |
where,
|
<math>~\mu</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{2}{\Chi + 1} \biggr]^{1 / 2}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{2 \sinh\eta \cdot \sinh\eta^' }{ \cosh(\eta^' + \eta) - \cos(\theta^' - \theta) } \biggr]^{1 / 2} \, .</math> |
The task is daunting, however, if the desire is to evaluate the expression for <math>~\Phi_\mathrm{CT}</math> analytically. To our knowledge, no one has yet been able to start from the expression as presented here for <math>~\Phi_\mathrm{CT}</math> and complete the integral over the angular coordinate, <math>~\theta^'</math>, analytically, let alone analytically evaluate the second, radial integral. This is principally because the integrand of the first (angular) integral contains a nontrivial function multiplied by a special function whose argument is, itself, a nontrivial function of both <math>~\theta^'</math> and <math>~\eta^'</math>.
W
At first glance, the expression for <math>~\Phi_\mathrm{W}</math> is much more complex than the expression for <math>~\Phi_\mathrm{CT}</math>. It not only requires a double integration, but also an infinite-series summation over the integer index, <math>~n</math>; and the radial integrand contains a product of two (relatively unfamiliar) associated Legendre functions of various half-integer orders (toroidal functions). Developing a numerical algorithm to evaluate <math>~\Phi_\mathrm{W}</math> to a certain accuracy — presumably set by the number of terms included in the summation over <math>~n</math> — would certainly be a more challenging task than developing a numerical algorithm to evaluate <math>~\Phi_\mathrm{CT}</math>.
Analytic Integration Over the Angular Coordinate
However, focusing only on the integration over the angular coordinate, we see that the integrand in the expression for <math>~\Phi_\mathrm{W}</math> is significantly less imposing than the one that appears in the expression for <math>~\Phi_\mathrm{CT}</math>. Wong (1973) was able to evaluate this definite integral in closed form, analytically. While Wong does not record the detailed steps that he used to evaluate this definite integral, he does indicate that he received guidance from Volume I of A. Erdélyi's (1953) Higher Transcendental Functions. We therefore presume that he adopted the line of reasoning that we have detailed in the Appendix, below, in deriving the expression labeled ③. Wong recognized, what we have explicitly demonstrated, namely,
|
<math>~\int_{-\pi}^\pi d\theta^' (\cosh\eta^' - \cos\theta^')^{- 5 / 2} \cos[n(\theta - \theta^')]</math> |
<math>~=</math> |
<math>~2\cos(n\theta) \int_0^\pi \frac{ \cos(n\theta^')~d\theta^' }{ (\cosh\eta^' - \cos \theta^')^{\frac{5}{2}} } </math> |
<math>~=</math> |
<math>~ \frac{8\sqrt{2}}{3} \biggl[ \frac{\cos(n\theta)}{\sinh^2\eta^'} \biggr] Q^2_{n- \frac{1}{2}} (\cosh\eta^') \,. </math> |
|
Wong (1973), p. 293, Eq. (2.56) |
||||
|
CAUTION: It is important to appreciate that, in this expression as well as in the expressions to follow, the term, <math>~Q^2_{n-\frac{1}{2}}(z)</math>, is not the square of the zero-order toroidal function, <math>~Q^0_{n - \frac{1}{2}}(z)</math>, but is instead the toroidal function of order two. In an accompanying discussion we present an analytic expression for <math>~Q^2_{-\frac{1}{2}}(z)</math> — and a separate analytic expression for <math>~Q^1_{-\frac{1}{2}}(z)</math> — in terms of complete elliptic integrals, as well as a recurrence relation that can be used to generate analytic expressions for all other order-two (and all other order-one) toroidal functions that have higher half-integer degrees, <math>~n-\tfrac{1}{2}</math> for <math>~n \ge 1</math>. |
Hence, Wong was able to simplify the expression for <math>~\Phi_\mathrm{W}</math> to one that — albeit, in addition to an infinite summation over the index, <math>~n</math> — only requires integration over the radial coordinate, <math>~\eta^'</math>. Specifically, he obtained,
|
<math>~\Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2G \rho_0 a^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \int_{\eta_0}^\infty d\eta^' ~\sinh\eta^'~P_{n-1 / 2}(\cosh\eta_<) ~Q_{n-1 / 2}(\cosh\eta_>)\biggl\{ \frac{8\sqrt{2}}{3} \biggl[ \frac{\cos(n\theta)}{\sinh^2\eta^'} \biggr] Q^2_{n- \frac{1}{2}} (\cosh\eta^') \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \biggl( \frac{16\sqrt{2}}{3} \biggr) G \rho_0 a^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) \int_{\eta_0}^\infty d\eta^' \Biggl[ \frac{Q^2_{n- \frac{1}{2}} (\cosh\eta^')}{\sinh\eta^'} \Biggr] ~P_{n-1 / 2}(\cosh\eta_<) ~Q_{n-1 / 2}(\cosh\eta_>) \, . </math> |
|
Wong (1973), p. 294, Eq. (2.57) |
||
Analytic Integration Over the Radial Coordinate
Now, in considering how to handle integration over the radial coordinate, <math>~\eta^'</math>, let's examine, first, the case where <math>~\eta^' \ge \eta_0 > \eta</math>, that is, the potential is being evaluated at a location that is entirely outside of the torus. In this case,
|
<math>~\Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - \biggl( \frac{16\sqrt{2}}{3} \biggr) G \rho_0 a^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) ~P_{n-1 / 2}(\cosh\eta) \int_{\eta_0}^\infty d\eta^' \Biggl[ \frac{Q^2_{n- \frac{1}{2}} (\cosh\eta^')}{\sinh\eta^'} \Biggr] ~Q_{n-1 / 2}(\cosh\eta^') \, . </math> |
So we are interested in carrying out the "radial" integral,
|
<math>~ \int_{\eta_0}^\infty d\eta^' \sinh\eta^' \Biggl[ \frac{Q^2_{n- \frac{1}{2}} (\cosh\eta^')}{\sinh^2\eta^'} \Biggr] ~Q_{n-1 / 2}(\cosh\eta^') </math> |
<math>~=</math> |
<math>~ \int_{\cosh(\eta_0)}^{\cosh(\infty)} dt \Biggl[ \frac{Q^2_{n- \frac{1}{2}} (t)~Q_{n-\frac{1}{2}}(t)}{t^2 - 1} \Biggr] \, , </math> |
where we have made the association, <math>~\cosh\eta^' \rightarrow t</math>, in which case, <math>~dt = \sinh\eta^' d\eta^'</math>. Following the line of reasoning that we have detailed in the Appendix, below, in deriving the expression labeled ④, this integral can be evaluated in closed form to give,
|
<math>~ \int_a^b\biggl[ \frac{Q_{n - \frac{1}{2}}^2(t) ~Q_{n - \frac{1}{2}}(t) }{(t^2-1)}\biggr]~dt </math> |
<math>~=</math> |
<math>~ \frac{1}{4} \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t) ~ Q_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr]_a^b \, . </math> |
|
Wong (1973), Eq. (2.58) |
||
Hence, we have,
|
<math>~\Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - \biggl( \frac{4\sqrt{2}}{3} \biggr) G \rho_0 a^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times P_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t) ~ Q_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr]_{t = \cosh \eta_0}^{t = \cosh\infty} \, . </math> |
Or, given that, in this uniform-density configuration, the density is exactly the mass divided by the torus volume, that is,
|
<math>~\rho_0 = \frac{M}{V}</math> |
<math>~=</math> |
<math>~\frac{M \sinh^3\eta_0}{2\pi^2 a^3 \cosh{\eta_0}} \, ,</math> |
we have,
|
<math>~\Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - \frac{2\sqrt{2}~ GM}{3\pi^2 a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times P_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t) ~ Q_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr]_{t = \cosh \eta_0}^{t = \cosh\infty} \, . </math> |
In a separate chapter, we have examined the asymptotic behavior of the toroidal functions, <math>~Q_{n-\tfrac{1}{2}}(t)</math>, which is,
|
<math>~\lim_{\chi\rightarrow \infty} Q_{n-\frac{1}{2}}(t)</math> |
<math>~\propto</math> |
<math>~ \frac{1}{t^{n+\frac{1}{2}} } \, . </math> |
This means that, at the upper integration limit, these toroidal functions go to zero. As a result, we can write,
| Exterior Solution: <math>~\eta_0 \ge \eta</math> | ||||||
|
This expression matches the potential for the exterior region that is obtained by combining Wong's (1973) Eqs. (2.59), (2.61) and (2.63).
Now, let's examine the potential evaluated at a radial location, <math>~\eta</math>, that is positioned inside the surface of the torus. That is, <math>~\eta_0 < \eta \le \infty</math>. We need to add expressions that have two different sets of integration limits as follows. First, over the subregion, <math>~\eta \le \eta^' \le \infty</math>, we use the same expression for <math>~\Phi_\mathrm{W}</math> but employ the new limits, as indicated; and second, over the subregion <math>~\eta_0 \le \eta^' \le \eta</math>, we swap the roles of <math>~P_{n-\frac{1}{2}}</math> and <math>~Q_{n-\frac{1}{2}}</math>.
|
<math>~\Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ \Phi_\mathrm{W}|_\mathrm{subregion1} + \Phi_\mathrm{W}|_\mathrm{subregion2} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2\sqrt{2}~ GM}{3\pi^2 a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times P_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t) ~ Q_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr]_{t = \cosh \eta}^{t = \cosh\infty} </math> |
|
|
|
<math>~ - \frac{2\sqrt{2}~ GM}{3\pi^2 a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times Q_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t) ~ P_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr]_{t = \cosh \eta_0}^{t = \cosh\eta} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2\sqrt{2}~ GM}{3\pi^2 a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times \biggl\{ P_{n-1 / 2}(\cosh\eta) \biggl[ (n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh\eta) Q_{n - \frac{1}{2}}^2(\cosh\eta) - (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(\cosh\eta) ~ Q_{n - \frac{1}{2}}(\cosh\eta) \biggr] </math> |
|
|
|
<math>~ + Q_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(\cosh\eta) ~ P_{n - \frac{1}{2}}(\cosh\eta) - (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh\eta) Q_{n - \frac{1}{2}}^2(\cosh\eta) \biggr] </math> |
|
|
|
<math>~ - Q_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(\cosh{\eta_0}) ~ P_{n - \frac{1}{2}}(\cosh{\eta_0}) - (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh{\eta_0}) Q_{n - \frac{1}{2}}^2(\cosh{\eta_0}) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2\sqrt{2}~ GM}{3\pi^2 a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times \biggl\{ P_{n-1 / 2}(\cosh\eta) \biggl[ (n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh\eta) Q_{n - \frac{1}{2}}^2(\cosh\eta) \biggr] - Q_{n-1 / 2}(\cosh\eta) \biggl[ (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh\eta) Q_{n - \frac{1}{2}}^2(\cosh\eta) \biggr] </math> |
|
|
|
<math>~ - Q_{n-1 / 2}(\cosh\eta) \biggl[ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(\cosh{\eta_0}) ~ P_{n - \frac{1}{2}}(\cosh{\eta_0}) - (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh{\eta_0}) Q_{n - \frac{1}{2}}^2(\cosh{\eta_0}) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2\sqrt{2}~ GM}{3\pi^2 a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) </math> |
|
|
|
<math>~ \times \biggl\{ Q_{n-1 / 2}(\cosh\eta) \biggl[ (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh{\eta_0}) Q_{n - \frac{1}{2}}^2(\cosh{\eta_0})
- (n - \tfrac{3}{2}) ~ P_{n - \frac{1}{2}}(\cosh{\eta_0})~Q^2_{n + \frac{1}{2}}(\cosh{\eta_0}) \biggr] </math> |
|
|
|
<math>~ - (n+\tfrac{1}{2})Q_{n - \frac{1}{2}}^2(\cosh\eta) \biggl[ Q_{n-1 / 2}(\cosh\eta) P_{n+\frac{1}{2}}(\cosh\eta) - Q_{n+\frac{1}{2}}(\cosh\eta) P_{n-1 / 2}(\cosh\eta) \biggr] \biggr\} </math> |
Drawing on the identified "Key Equation" expression,
|
<math>~(\xi - z)\sum_{m=0}^n (2m+1)P_m(z) Q_m(\xi)</math> |
<math>~=</math> |
<math>~ 1 - (\ell+1)[P_{\ell+1}(z) Q_\ell(\xi) - P_\ell(z)Q_{\ell+1}(\xi)] </math> |
|
|
Abramowitz & Stegun (1995), p. 335, eq. (8.9.2) |
|||
and adopting the associations, <math>~z = \xi = \cosh\eta</math> and <math>~\ell \rightarrow (n-\tfrac{1}{2})</math>, we recognize that,
|
<math>~(n+\tfrac{1}{2})[P_{n+\frac{1}{2}}(\cosh\eta) Q_{n-\frac{1}{2}} (\cosh\eta) - P_{n-\frac{1}{2}}(\cosh\eta)Q_{n+\frac{1}{2}}(\cosh\eta)] </math> |
<math>~=</math> |
<math>~ 1 \, . </math> |
Hence, we can write,
| Interior Solution: <math>~\eta \ge \eta_0 </math> | ||||||
|
This expression matches the potential for the interior region that is obtained by combining Wong's (1973) Eqs. (2.59), (2.60) and (2.62). Finally, drawing on yet another identified "Key Equation," namely,
|
<math>~ Q_{-\frac{1}{2}}^\mu(z) + 2\sum_{n=1}^\infty Q^\mu_{n-\frac{1}{2}}(z) \cos(n\nu) </math> |
<math>~=</math> |
<math>~ e^{i\mu\pi}~\biggl(\frac{\pi}{2} \biggr)^{1 / 2} \Gamma(\mu + \tfrac{1}{2})\biggl[ \frac{(z^2-1)^{\mu/2}}{(z - \cos\nu)^{\mu + \frac{1}{2}}} \biggr] </math> |
|
|
A. Erdélyi (1953): Volume I, §3.10, p. 166, eq. (3) |
|||
| Valid for: |
<math>~\mathrm{Re}~\mu > - \tfrac{1}{2}</math> |
and adopting the associations, <math>~\mu \rightarrow 2</math>, <math>~\nu \rightarrow \theta</math>, and <math>~z \rightarrow \cosh\eta</math>, we see that,
|
<math>~ \sum_{n=0}^\infty \epsilon_n \cos(n\theta) ~Q^2_{n-\frac{1}{2}}(\cosh\eta) </math> |
<math>~=</math> |
<math>~ (-1)^2~\biggl(\frac{\pi}{2} \biggr)^{1 / 2} \Gamma(2 + \tfrac{1}{2})\biggl[ \frac{ \sinh^2\eta }{(\cosh\eta - \cos\theta)^{\frac{5}{2}}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{\pi}{2} \biggr)^{1 / 2} \biggl[ \frac{4! \sqrt{\pi}}{ 4^2 \cdot 2! } \biggr] \biggl[ \frac{ \sinh^2\eta }{(\cosh\eta - \cos\theta)^{\frac{5}{2}} } \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{1}{2} \biggr)^{1 / 2} \biggl[ \frac{ 3\pi}{ 2^2} \biggr] \biggl[ \frac{ \sinh^2\eta }{(\cosh\eta - \cos\theta)^{\frac{5}{2}} } \biggr] \, . </math> |
|
Wong (1973), Eq. (2.64) |
||
Hence, the interior solution can be rewritten as,
|
<math>~\Phi_\mathrm{W}(\eta,\theta)\bigr|_\mathrm{interior}</math> |
<math>~=</math> |
<math>~ \frac{ GM}{2\pi a} \biggl[ \frac{\sinh^3\eta_0}{ \cosh{\eta_0}} \biggr] \biggl\{ \biggl[ \frac{ \sinh\eta }{(\cosh\eta - \cos\theta) } \biggr]^2 ~ - ~ \frac{2^2\sqrt{2}~ }{3\pi} (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \cos(n\theta) \, . </math> |
|
|
|
<math>~ \times Q_{n-1 / 2}(\cosh\eta) \biggl[ (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh{\eta_0}) Q_{n - \frac{1}{2}}^2(\cosh{\eta_0})
- (n - \tfrac{3}{2}) ~ P_{n - \frac{1}{2}}(\cosh{\eta_0})~Q^2_{n + \frac{1}{2}}(\cosh{\eta_0}) \biggr] \biggr\} \, . </math> |
|
Wong (1973), Eq. (2.65) |
||
Evaluation
Composite Gravitational Potential
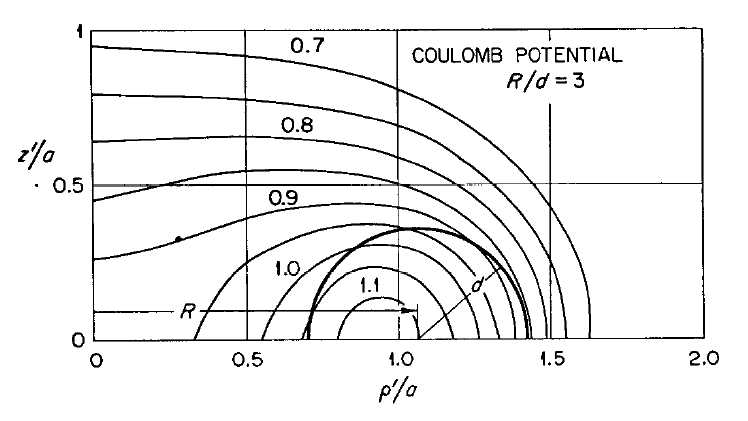
In order to illustrate how the potential behaves both inside and outside (in the immediate vicinity) of a uniform-density torus, Wong (1973) set <math>~R/d = \cosh\eta_0 = 3</math> and evaluated the pair of boxed-in expressions for <math>~\Phi_\mathrm{W}(\eta,\theta)</math> given above, over most of the cylindrical-coordinate range, <math>~0 \le \varpi/a \le 2.0</math> and <math>~0 \le z/a \le 1.0</math>. (He certainly truncated the series summation at a finite number of terms, but his article does not state how many terms he included.) The meridional-plane contour plot that resulted from this evaluation appears as Figure 7 in Wong (1973) and has been reprinted here, unaltered, in the top panel of our Figure 1.
| Figure 1 |
|---|
|
Figure 7 extracted without modification from p. 297 of Wong (1973)
"Toroidal and Spherical Bubble Nuclei"
Annals of Physics, vol. 77, pp. 279-353 © Elsevier Science |
|
Figure Caption: Contours of the Coulomb (gravitational) potential in the meridional plane for a uniformly charged (uniform-density) torus with an aspect ratio, <math>~R/d = \cosh\eta_0 = 3</math>. (Top) Figure 7 extracted without modification from Wong (1973). (Bottom) Contour plot resulting from our numerical evaluation of Wong's analytically specified potential, <math>~\Phi_\mathrm{w}</math>. The toroidal coordinate system's anchor ring is located at position <math>~(\varpi/a, z/a) = (1.0,0.0)</math>, as explicitly identified by the axis label (top panel), and as marked by a small purple circular marker (bottom panel). The circular cross-section of the torus is identified by the thick-black semicircle (top panel) and by the black circle (bottom panel). The center of this toroidal cross-section lies just outside the location of the anchor ring at the radial-coordinate position, <math>~R/a = [1 - (R/d)^{-2}]^{- 1 / 2} = 3/2^{3 / 2} </math>; this position is marked by a small white circular marker in the bottom panel. Notice that the absolute potential minimum is positioned just inside the location of the anchor ring. |
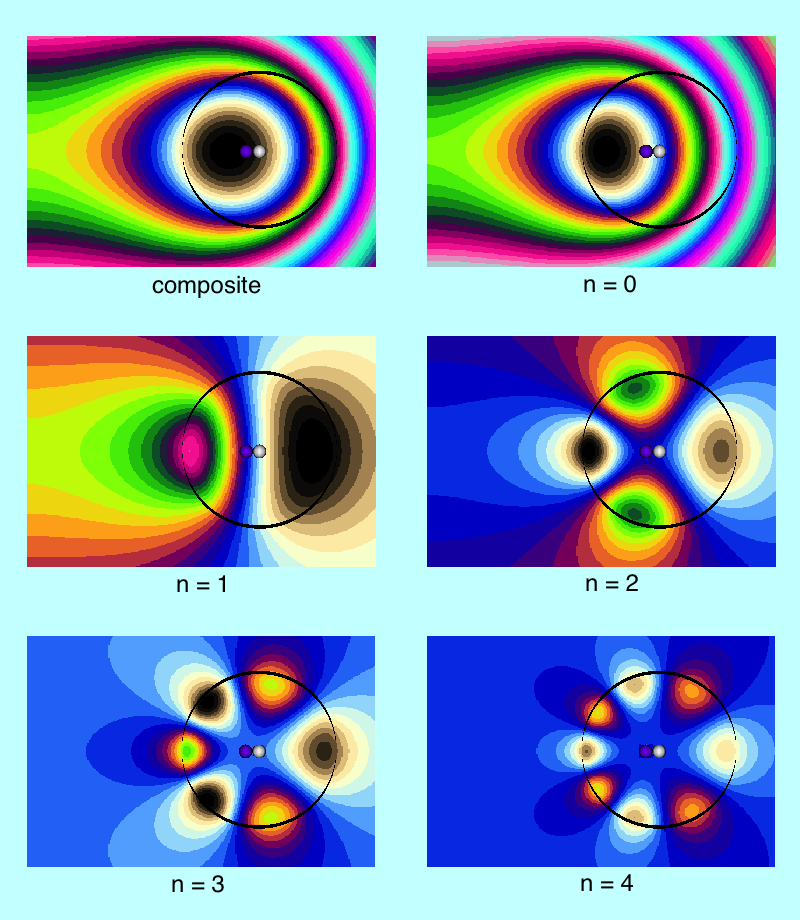
We have also evaluated Wong's (1973) derived potential function, <math>~\Phi_\mathrm{W}(\eta,\theta)</math>, both inside and outside (in the immediate vicinity) of a uniform-density torus whose aspect ratio is, <math>~R/d = \cosh\eta_0 = 3</math>. (As is discussed further, below, we included only the terms, n = 0, 1, 2, & 3, in the series summation.) A colored contour plot resulting from our evaluation is displayed in the bottom panel of our Figure 1; the height and width of this rectangular image have been linearly scaled to lengths that allow straightforward — although regrettably not exact — comparison with Wong's (1973) published Figure 7. The Figure 1 caption highlights some specific points of comparison. Qualitatively, at least, our plotted contours match quite well the contours presented by Wong (1973).
In designing a numerical algorithm to evaluate <math>~\Phi_\mathrm{W}</math>, we first followed Wong's (1973) lead and rewrote the interior/exterior expressions in a more compact form. After defining the leading amplitude coefficient,
<math>~D_0 \equiv \frac{2^{3/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] \, ,</math>
and the pair of parameters,
|
<math>~B_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~ (n+\tfrac{1}{2})P_{n+\frac{1}{2}}(\cosh{\eta_0}) Q_{n - \frac{1}{2}}^2(\cosh{\eta_0}) - (n - \tfrac{3}{2}) ~ P_{n - \frac{1}{2}}(\cosh{\eta_0})~Q^2_{n + \frac{1}{2}}(\cosh{\eta_0}) \, , </math> |
|
<math>~C_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~(n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh \eta_0) Q_{n - \frac{1}{2}}^2(\cosh \eta_0) - (n - \tfrac{3}{2}) Q_{n - \frac{1}{2}}(\cosh \eta_0)~Q^2_{n + \frac{1}{2}}(\cosh \eta_0) \, , </math> |
each of which is only a function of the axis ratio of the torus (via the parameter <math>~\eta_0</math>) and the polar angle index, <math>~n</math>, the (dimensionless) expression for the potential becomes,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~\sum_{n=0}^{\mathrm{nmax}} \epsilon_n \cos(n\theta) A_n(\cosh\eta) \, , </math> |
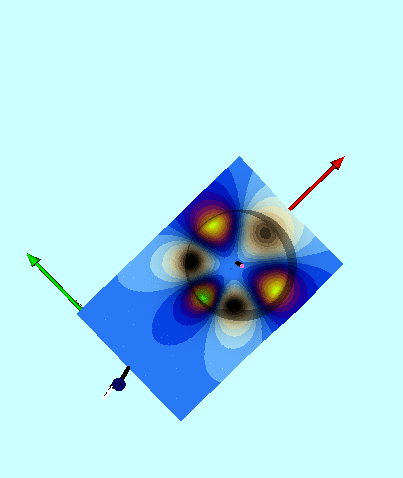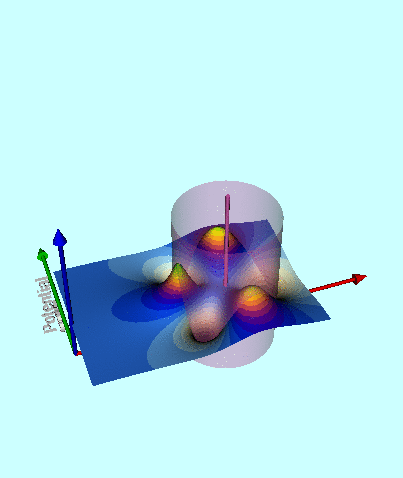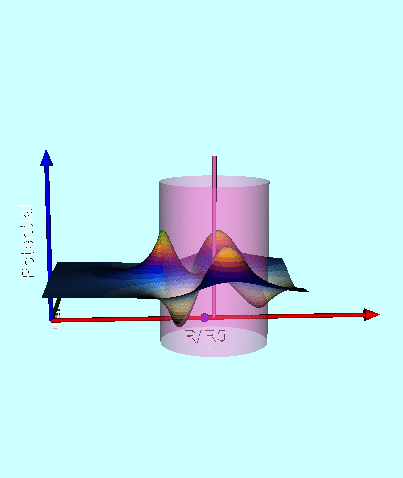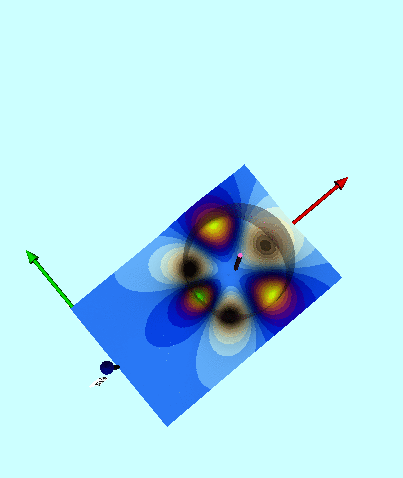
| Figure 2: 3D Animated Depiction of the Warped Surface of Wong's Toroidal Potential |
|---|
where,
|
<math>~A_n(\cosh\eta)\biggr|_\mathrm{interior}</math> |
<math>~=</math> |
<math>~B_n(\cosh\eta_0)Q_{n-\frac{1}{2}}(\cosh\eta) - Q^2_{n-\frac{1}{2}}(\cosh\eta)</math> |
| and | ||
|
<math>~A_n(\cosh\eta)\biggr|_\mathrm{exterior}</math> |
<math>~=</math> |
<math>~C_n(\cosh\eta_0)P_{n-\frac{1}{2}}(\cosh\eta) \, .</math> |
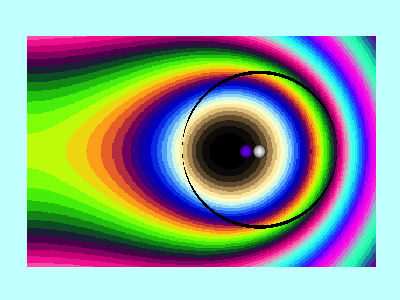
Next, in FORTRAN, we wrote a group of functions/subroutines that allowed us to evaluate the toroidal functions, <math>~P^0_{n-\frac{1}{2}}</math> and <math>~Q^m_{n-\frac{1}{2}}</math>, individually for m = 0, 1, & 2 and for all desired polar angle index values; a (double-precision version of a) set of Numerical Recipes algorithms was used to evaluate complete elliptic integrals of the first and second kind. An accompanying appendix provides details regarding some key tests that we conducted in order to demonstrate the accuracy of these various functions/subroutines. Then, as has already been stated, the (composite) meridional-plane contour diagram displayed in the bottom panel of Figure 1 was generated by setting <math>~R/d = \cosh\eta_0 = 3</math> and <math>~\mathrm{nmax} = 3</math>. A three-dimensional animated depiction of this same potential contour surface is displayed here, on the right. In an effort to better illustrate key features of the warped surface, different frames of the animation present the same surface as viewed from different lines of sight.
Elements of the accompanying 3D animated depiction:
- The pair of (cylindrical-coordinate based) meridional-plane axes are (red) <math>~\varpi/R_0</math> and (green) <math>~Z/R_0</math>, where <math>~R_0</math> is the distance in the equatorial plane from the symmetry axis to the center of the circular cross-section of the torus.
- The scalar value of the potential is plotted along the third (blue) axis; the surface, as a whole, has been shifted vertically in order to place the potential minimum at zero.
- The pink, translucent cylinder identifies the meridional-plane location of the surface of the torus; because the model being illustrated has an axis ratio, <math>~R_0/d = \cosh\eta_0 =3</math>, the radius of the pink cylinder is <math>~d/R_0 = 1/3</math>. This same cylindrical surface of the torus is identified by the thick black circle in the 2D projection of the warped contour surface that is displayed in the bottom panel of our Figure 1. A thin, pink vertical rod identifies the center of the circular cross-section of the (pink) torus; it intersects the red, radial-coordinate axis at the location that is identified in the middle panel of Figure 1 by a small white circular marker.
- As in the middle panel of Figure 1, a small spherical purple marker identifies radial location of the anchor ring associated with the adopted toroidal coordinate system.
Contribution from Individual Modes
| Figure 2: Contribution from Various Polar Angle Nodes | |
|---|---|
Appendix: Selected Toroidal Function Relationships
Here, we draw from the set of toroidal function relationships that have been identified as "Key Equations" in our accompanying Equations appendix. Two related appendices — numbered A.1 and A.2 — may be found in an accompanying discussion.
A.3
|
Our objective is to evaluate the definite integral,
Notice that, since the limits of the integration are <math>~-\pi</math> to <math>~+\pi</math>: The second integral on the right-hand-side goes to zero because the numerator of its integrand — i.e., <math>~\sin(n\theta)</math> — is an odd function; and, with regard to the first integral on the right-hand-side, the lower integration limit can be set to zero and the result doubled because the numerator of its integrand — i.e., <math>~\cos(n\theta)</math> — is an even function. Drawing from Volume I of A. Erdélyi's (1953) Higher Transcendental Functions, we find the following "Key Equation":
Next we adopt the associations, <math>~z \rightarrow \cosh\eta</math>, <math>~t \rightarrow \theta</math>, <math>~\mu \rightarrow 2</math>, and, <math>~\nu \rightarrow n - \tfrac{1}{2}</math>, where <math>~n</math> is zero or a positive integer. In this case we have,
where the prefactor of the second term — that is, <math>~\cos[(n-\tfrac{1}{2})\pi] </math> — goes to zero for all allowable values of the integer, <math>~n</math>. Hence, we conclude that,
where we have set, <math>~ \Gamma(\tfrac{5}{2}) = \Gamma(\tfrac{1}{2} + 2) = \frac{ \sqrt{\pi} \cdot 4! }{4^2 \cdot 2!} = \frac{\sqrt{\pi} \cdot 2^3\cdot 3}{ 2^5 } = \frac{3 \sqrt{\pi}}{2^2} \, . </math> |
|||||||||||||||||||||||||||||
A.4
|
Beginning with the identified "Key Equation",
we will adopt the associations: <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 2</math>, <math>~\nu \rightarrow (n - \tfrac{1}{2})</math>, <math>~\rho \rightarrow 0</math>, and <math>~\sigma \rightarrow ( n - \tfrac{1}{2})</math>. As a result, Erdélyi's (1953) expression becomes,
Drawing upon the recurrence "Key Equation,"
which means, after making the associations, <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 0</math> and <math>~\nu \rightarrow (n-\tfrac{1}{2})</math>, that,
the integral can be rewritten as,
Returning to the same recurrence "Key Equation," but this time adopting the associations, <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 2</math> and <math>~\nu \rightarrow (n-\tfrac{1}{2})</math>, we can write,
in which case the integral becomes,
|
||||||||||||||||||||||||||||||||||||||||
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |