Overview: Marginally Unstable Pressure-Truncated Configurations

Additional details may be found here.

Isothermal

The internal structure of a detailed force-balance model is provided via the function, <math>~\psi(\xi)</math>, which is a solution to the,

Isothermal Lane-Emden Equation

<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>

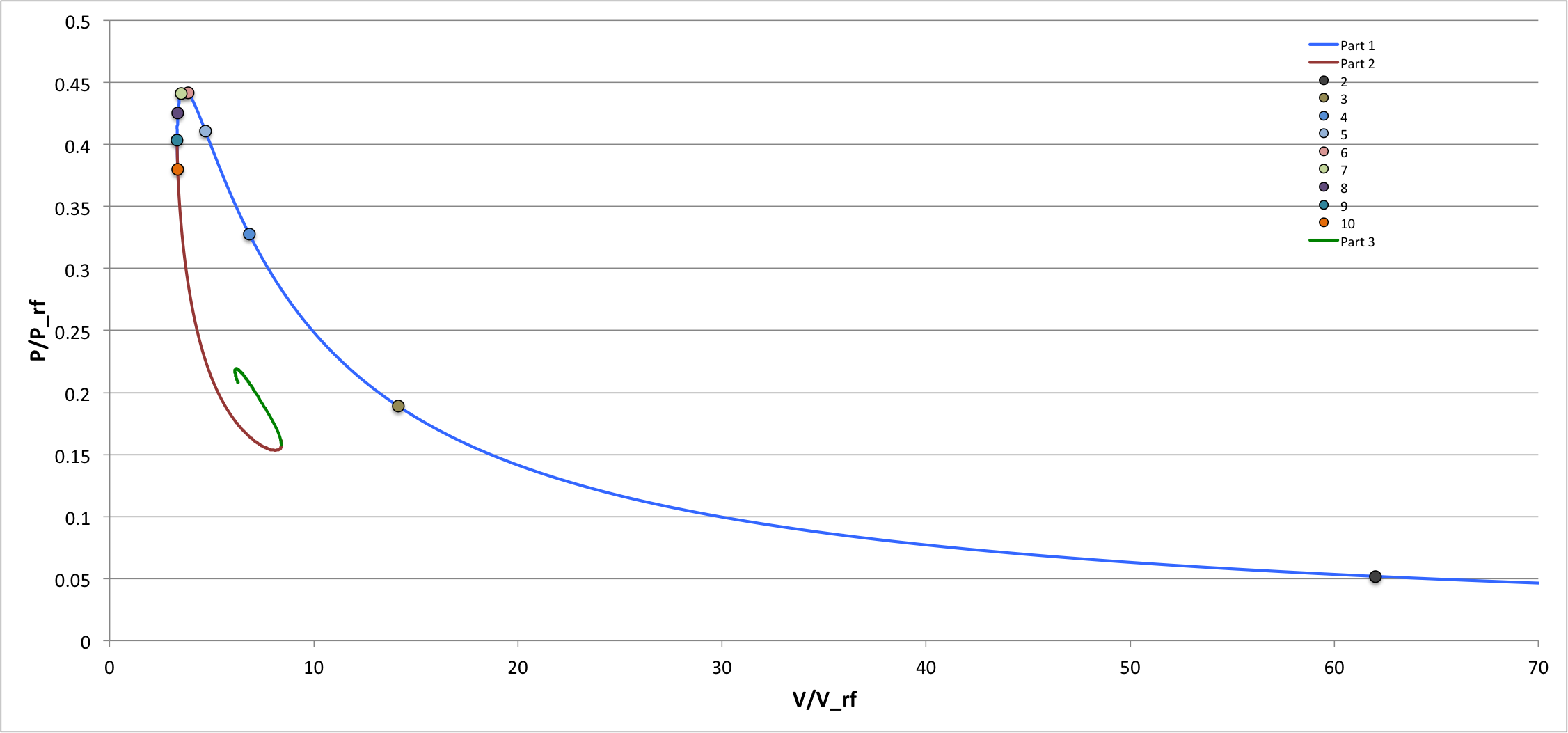
Equilibrium sequence for pressure-truncated configurations is displayed in three ways.

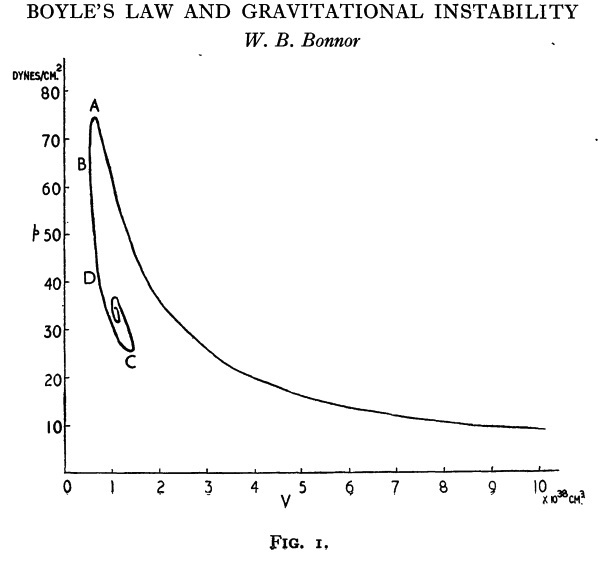
Figure 1: Bonnor's P-V Diagram (see related discussion)

This equation — in the following, slightly rewritten form — can be found among our selected set of key equations associated with the study of radial pulsation, and will henceforth be referred to as the,

Isothermal LAWE

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math>
where: <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math> and, <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

Yabushita (1974, 1975) showed that one valid,

Precise Solution to the Isothermal LAWE
<math>~\sigma_c^2 = 0</math>	and	<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, .</math>

When viewed in concert with the surface boundary condition,

the relevant configuration is precisely defined by the surface condition, xxx, which is identical to the configuration at the turning point.