Radial Oscillations of n = 3 Polytropic Spheres

Background

Our Formulation of the Problem

In an accompanying discussion, we derived the so-called,

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. Because this widely used form of the radial pulsation equation is not dimensionless but, rather, has units of inverse length-squared, we have found it useful to also recast it in the following dimensionless form:

<math> \frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 , </math>

where,

<math>~g_\mathrm{SSC} \equiv \frac{P_c}{R\rho_c} \, ,</math> and <math>~\tau_\mathrm{SSC} \equiv \biggl[\frac{R^2 \rho_c}{P_c}\biggr]^{1/2} \, .</math>

In a separate discussion, we showed that specifically for isolated, polytropic configurations, this linear adiabatic wave equation (LAWE) can be rewritten as,

<math>~0 </math>	<math>~=</math>	<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\frac{\omega^2}{\gamma_g \theta} \biggl(\frac{n+1 }{4\pi G \rho_c} \biggr) - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>
	<math>~=</math>	<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] \frac{dx}{d\xi} + \frac{(n+1)}{\theta}\biggl[\frac{\sigma_c^2}{6\gamma_g } - \frac{\alpha}{\xi} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] x \, ,</math>

where we have adopted the dimensionless frequency notation,

<math>~\sigma_c^2</math>

<math>~\equiv</math>

<math>~\frac{3\omega^2}{2\pi G \rho_c} \, .</math>

In this chapter we carry out a numerical integration of this governing LAWE for <math>~n=3</math> polytropes. The results are presented below.

Schwarzschild (1941)

We can directly compare our results with Schwarzschild's (1941) published work on "Overtone Pulsations for the Standard [Stellar] Model." To begin with, it is straightforward to demonstrate that the last form of the LAWE, provided above, matches equation (2) from Schwarzschild (1941), if <math>~n</math> is set to 3 — see the boxed-in excerpt, immediately below. Note as well that Schwarzschild's dimensionless oscillation frequency — defined in his equation (1) and which we will label, <math>~\omega_\mathrm{Sch}</math> — is related to our dimensionless frequency via the expression,

<math>~\sigma_c^2</math>

<math>~~\leftrightarrow~~</math>

<math>~\biggl( \frac{3\gamma_g}{2} \biggr) \omega_\mathrm{Sch}^2 \, .</math>

Schwarzschild (1941) numerically integrated the LAWE for <math>~n=3</math> polytropic spheres to find eigenvectors (i.e., the spatially discrete eigenfunction and corresponding eigenfrequency) for five separate oscillation modes (the fundamental mode, plus the 1^st, 2^nd, 3^rd, and 4^th overtones) for models having four different adopted adiabatic indexes <math>~\gamma_g = \tfrac{4}{3}, \tfrac{10}{7}, \tfrac{20}{13}, \tfrac{5}{3})</math>.

Paragraph extracted from M. Schwarzschild (1941)

"Overtone Pulsations for the Standard Model"

ApJ, vol. 94, pp. 245 - 252 © American Astronomical Society

³A. S. Eddington (1930), The Internal Constitution of the Stars, pp. 188 and 192.

Drawing from our discussion of the historical treatment of boundary conditions, we presume that Schwarzschild imposed the following constraint at the surface:

<math>~\frac{d\ln x}{d\ln \xi}\biggr\|_\mathrm{surface}</math>	<math>~=</math>	<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) </math>
	<math>~=</math>	<math>~\biggl[ \frac{3\omega^2 R^3}{4\pi G \gamma \bar\rho} - \alpha \biggr] </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl[ \frac{\sigma_c^2}{\gamma } \biggl(\frac{\rho_c}{\bar\rho}\biggr) -2 \alpha \biggr] </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ \biggl[ \mathfrak{F} + 2\alpha \biggr] \biggl(\frac{\rho_c}{\bar\rho}\biggr) -2 \alpha \biggr\} \, .</math>

Recognizing from an accompanying tabulation that, for <math>~n=3</math> polytropes,

<math>~\approx</math>

we presume that the surface boundary condition imposed by Schwarzschild was,

<math>~\frac{d\ln x}{d\ln \xi}\biggr|_\mathrm{surface}</math>

<math>~27.09124 ( \mathfrak{F} + 2\alpha ) - \alpha \, .</math>

Our Table 1 catalogs the eigenfrequencies that Schwarzschild determined (drawn from his Table 1) for these twenty different models/modes.

Table 1: From Table 1 of M. Schwarzschild (1941)
Mode	<math>~\alpha = 0.0</math> <math>~(\gamma_g = 4/3)</math>	<math>~\alpha = 0.2</math> <math>~(\gamma_g = 10/7)</math>	<math>~\alpha = 0.4</math> <math>~(\gamma_g = 20/13)</math>		<math>~\alpha = 0.6</math> <math>~(\gamma_g = 5/3)</math>
Mode	<math>~\omega_\mathrm{Sch}^2</math>	<math>~\omega_\mathrm{Sch}^2</math>	<math>~\omega_\mathrm{Sch}^2</math>	<math>~\mathfrak{F} = \biggl[\frac{3\omega_\mathrm{Sch}^2}{2} - 2\alpha \biggr]</math>	<math>~\omega_\mathrm{Sch}^2</math>
0	0.00000	0.05882	0.10391	-0.64414	0.13670
1	0.16643	0.19139	0.21998	-0.47003	0.25090
2	0.3392	0.3648	0.3920	-0.2120	0.4209
3	0.5600	0.5863	0.6136	+0.1204	0.6420
4	0.8283	0.8554	0.8832	+0.5248	0.9117

Schwarzschild (1941) also documented the radial structure of the eigenfunction that is associated with each of these twenty model/mode eigenfrequencies. Each column of his Table 4, except the first, presents numerical values of the amplitude of a specific model/mode at 84 discrete radial locations throughout the n = 3 polytrope; the first column of the table lists the corresponding radial coordinate, <math>~\xi</math>. Focusing on the model that he analyzed assuming <math>~\alpha = 0.4</math>, we have typed his five columns of data into an Excel spreadsheet and have used this data to generate the pair of plots displayed, below, in Figure 1. The left-hand panel displays the eigenfunction amplitude versus radius, <math>~x(\xi)</math>, for the fundamental mode as well as for the first four overtones; it essentially replicates Figure 1 from Schwarzschild (1941). The right-hand panel displays the same data, but as a semi-log plot; specifically, it displays <math>~y(\xi)</math>, where,

<math>~y \equiv \frac{1}{2} \log_{10}[x^2 + 10^{-8}] \, .</math>

Each sharp valley in this semi-log plot highlights the location of a node in the corresponding eigenfunction, that is, it identifies where <math>~x(\xi)</math> crosses through zero.

Figure 1: Schwarzschild's Eigenfunctions for an n = 3 Polytrope with α = 0.4 (γ = 20/13)

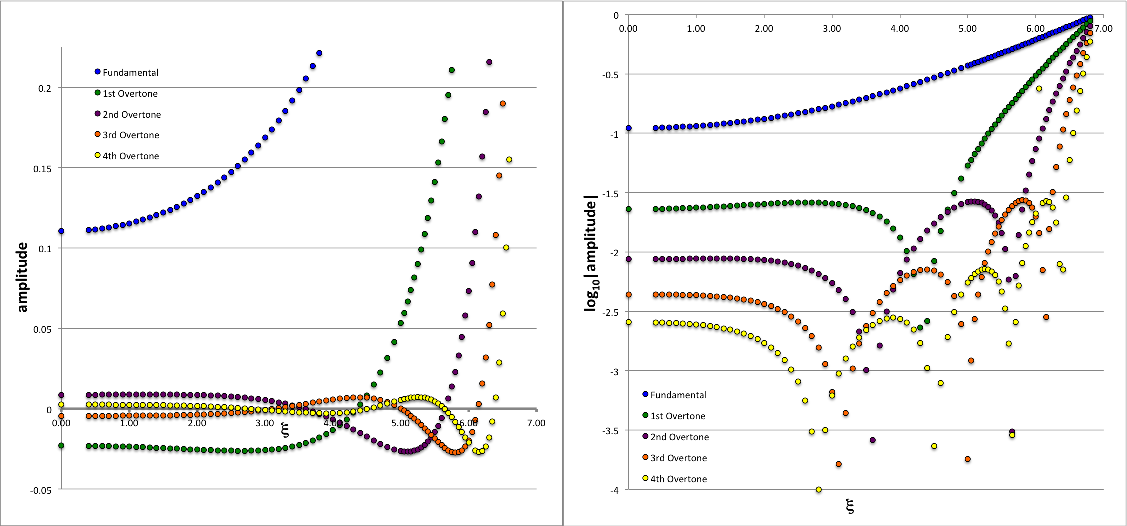Numerical Integration

From the Core to the Surface

Here we use the finite-difference algorithm described separately to integrate the discretized LAWE from the center of the polytropic configuration, outward to its surface, which in this case — see, for example, p. 77 of Horedt (2004) — is located at the polytropic-coordinate location,

<math>~\xi_\mathrm{max} = 6.89684862 \, .</math>

It is assumed, at the outset, that we have in hand an appropriately discretized description of the unperturbed, equilibrium properties of an <math>~n=3</math> polytrope; specifically, at each radial grid line, we have tabulated values of the radial coordinate, <math>~0 \le \xi_i \le \xi_\mathrm{max}</math>, the Lane-Emden function, <math>~\theta_i</math>, and its first radial derivative, <math>~\theta_i'</math>.

The algorithm is as follows (substitute <math>~n=3</math> everywhere):

Establish an equally spaced radial-coordinate grid containing <math>~N</math> grid zones (and, accordingly, <math>~N+1</math> grid lines), in which case the grid-spacing parameter, <math>~\Delta_\xi \equiv \xi_\mathrm{max}/N</math>.
Specify a value of the adiabatic exponent, <math>~\gamma</math>, which, in turn, determines the value of the parameter, <math>~\alpha \equiv (3-4/\gamma) \, .</math>
Choose a value for the (square of the) dimensionless oscillation frequency, <math>~\sigma_c^2</math>, which we will accomplish by assigning a value to the parameter,

<math>~\mathfrak{F} \equiv \frac{\sigma_c^2}{\gamma} - 2\alpha \, .</math>
Set the eigenfunction to unity at the center <math>~(\xi_0 = 0)</math> of the configuration, that is, set <math>~x_0 = 1</math>.
Determine the value of the eigenfunction at the first grid line away from the center — having coordinate location, <math>~\xi_1 = \Delta_\xi </math> — via the expression,

<math>~ x_1 </math>

<math>~=</math>

<math>~ x_0 \biggl[ 1 - \frac{\Delta_\xi^2 (n+1) \mathfrak{F}}{12} \biggr] \, .</math>

At all other grid lines, <math>~i=2,N</math>, determine the value of the eigenfunction, <math>~x_i</math>, via the expression,

<math>~x_i \biggl[2\theta_{i-1} +\frac{4\Delta_\xi \theta_{i-1}}{\xi_{i-1}} - \Delta_\xi (n+1)(- \theta^')_{i-1}\biggr] </math>

<math>~ x_{i-1}\biggl\{4\theta_{i-1} - \frac{\Delta_\xi^2(n+1)}{3}\biggl[ \mathfrak{F}+2\alpha - 2\alpha \biggl(- \frac{3\theta^'}{\xi}\biggr)_{i-1} \biggr] \biggr\} + x_{i-2} \biggl[\frac{4\Delta_\xi \theta_{i-1}}{\xi_{i-1}} - \Delta_\xi (n+1)(- \theta^')_{i-1} - 2\theta_{i-1}\biggr] \, .</math>

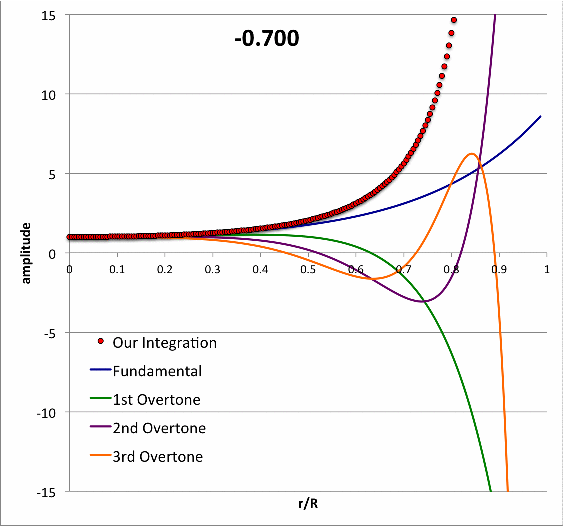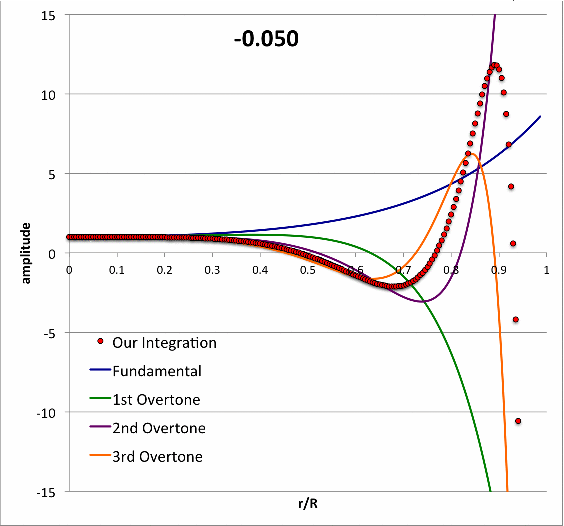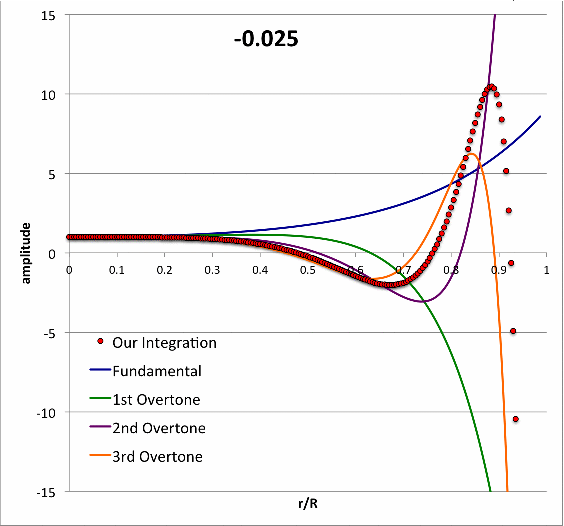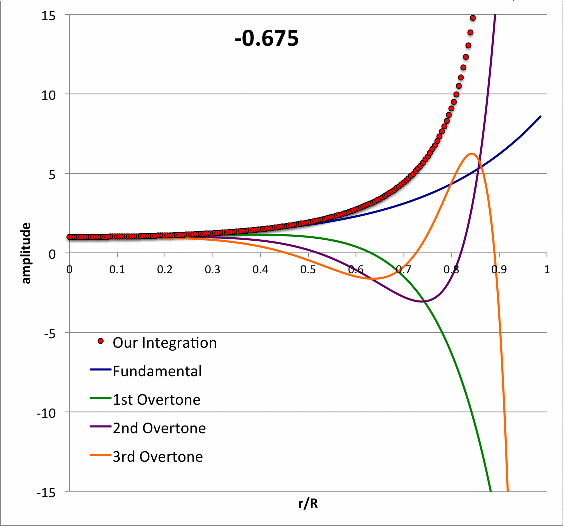
We divided our model into <math>~N = 200</math> radial zones and, using this algorithm, integrated the LAWE from the center of the configuration to the surface, for <math>~\alpha = 0.4</math>, and approximately 40 different chosen values of the frequency parameter across the range, <math>~-0.7 \le \mathfrak{F} \le + 0.3</math>. The radial displacement functions resulting from these integrations are presented in Figure 2 as an animation sequence. The specified value of <math>~\mathfrak{F}</math> is displayed at the top of each animation frame, and the resulting displacement function, <math>~x(r/R)</math>, is traced by the small, red circular markers in each frame.

Figure 2: Numerically Determined Eigenfunctions for Various <math>~\mathfrak{F}</math>

Table 2
Mode	Match Schwarzschild	Match B.C.
Mode	<math>~\mathfrak{F}</math>	<math>~\mathfrak{F}</math>
0	-0.644131578154	-0.644131577959
1	-0.47013976423	-0.47013975308
2	-0.2121284391	-0.2121282667
3	+0.1202565375	+0.120257856

Each frame of the Figure 2 animation also displays, as smooth solid curves, the radial eigenfunctions that Schwarzschild (1941) obtained for the fundamental mode (blue curve) and the first three overtone modes (green, purple, & orange curves, repectively) for his model with <math>~\alpha = 0.4</math>. These are the same curves that appear in the left-hand panel of Figure 1, but here the displacement amplitude has been renormalized such that <math>~x_0 = 1</math>, and, along the horizontal axis, the radial location is marked in terms of the fractional radius, <math>~r/R \equiv \xi/\xi_\mathrm{max}</math>. In our examination of this model, as we approached each specific value of a modal eigenfrequency identified by Schwarzschild — see the frequencies highlighted in pink in our Table 1 — we fine-tuned our choice of the eigenfrequency in order to find a displacement function whose surface amplitude matched, to a high level of precision, the surface amplitude associated with Schwarzschild's corresponding published eigenfunction. The column of our Table 2 whose heading is "Match Schwarzschild" identifies — to at least 10 digits precision — the frequency choice that was required in order for these surface amplitudes to match in each case.

It is gratifying to see that our resulting frequencies match well the values published by Schwarzschild (as highlighted in pink, above). But this does not satisfactorily explain why, among the entire range of displacement functions displayed (in red) in the Figure 2 animation, Schwarzschild labeled these specific ones as the eigenmodes. As we shall now demonstrate, his eigenmode identifications resulted from the imposition of a specific, physically justified constraint on the slope, rather than the value, of the displacement function at the surface of the configuration.

Surface Boundary Condition

As was stated, above, we presume that as Schwarzschild searched for natural modes of oscillation in isolated, <math>~n=3</math> polytropes, he imposed the following boundary condition at the surface of the configuration:

<math>~\frac{d\ln x}{d\ln \xi}\biggr|_\mathrm{surface}</math>

<math>~27.09124 ( \mathfrak{F} + 2\alpha ) - \alpha \, .</math>

In order to duplicate his findings, then, we need to fine tune our specification of the oscillation frequency such that the resulting displacement function presents this behavior at the surface of our model. A finite-difference expression of this logarithmic derivative that is consistent with the above-described finite-difference algorithm, is,

<math>~\frac{d\ln x}{d\ln \xi} \biggr|_\mathrm{surface}</math>

<math>~\approx</math>

<math>~\frac{\xi_\mathrm{max}}{x_N} \biggl[ \frac{x_{N+1}-x_{N-1}}{2\Delta_\xi} \biggr] \, .</math>

Everything is known here, except for the quantity, <math>~x_{N+1}</math>, which can be evaluated using the last expression in our algorithm one more time to, in effect, evaluate the eigenfunction just outside the surface. That is, we obtain <math>~x_{N+1}</math> and, in turn, obtain a value for the logarithmic derivative at the surface, via the expression,

<math>~x_{N+1} \biggl[2\theta_{N} +\frac{4\Delta_\xi \theta_{N}}{\xi_\mathrm{max}} - \Delta_\xi (n+1)(- \theta^')_{N}\biggr] </math>

<math>~ x_{N}\biggl\{4\theta_{N} - \frac{\Delta_\xi^2(n+1)}{3}\biggl[ \mathfrak{F}+2\alpha - 2\alpha \biggl(- \frac{3\theta^'}{\xi}\biggr)_{N} \biggr] \biggr\} + x_{N-1} \biggl[\frac{4\Delta_\xi \theta_{N}}{\xi_\mathrm{max}} - \Delta_\xi (n+1)(- \theta^')_{N} - 2\theta_{N}\biggr] \, .</math>

We added to our numerical algorithm a step that evaluates, in this manner, the logarithmic derivative of the displacement function at the surface of our polytropic configuration. The eigenfrequencies that generated displacement functions with this surface behavior are listed for four separate modes in the column of Table 2 titled, "Match B.C." In every case the values agree to at least five decimal places with the "Match Schwarzschild" eigenfrequencies. We conclude, therefore, that it was the implementation of this surface boundary condition that permitted Schwarzschild to quantitatively identify the properties of the eigenvectors associated with natural radial modes of oscillation in <math>~n=3</math> polytropes.

Related Discussions

Radial Oscillations of Uniform-density sphere
Radial Oscillations of Isolated Polytropes
- Setup
- n = 1: Attempt at Formulating an Analytic Solution
- n = 3: Numerical Solution to compare with M. Schwarzschild (1941)
- n = 5: Attempt at Formulating an Analytic Solution

User:Tohline/SSC/Stability/n3PolytropeLAWE

Contents