Numerically Determined Eigenvectors of a Zero-Zero Bipolytrope

Here we build on the analytic foundation summarized in an accompanying chapter and attempt to numerically construct a variety of eigenvectors that describe radial oscillations of bipolytropes for which, <math>~(n_c, n_e) = (0,0)</math>.

Setup

We'll begin with the linear-adiabatic wave equations that describe oscillations of the core and envelope, separately. We also will immediately restrict our investigation to configurations for which,

<math>~g^2 = \mathcal{B} </math> <math>~\Rightarrow</math> <math>~g^2 = \frac{1+8q^3}{ (1+2q^3)^2 } \, ,</math> and, <math>~q^3 = \mathcal{D} = \biggl[ \frac{\rho_e/\rho_c}{2(1-\rho_e/\rho_c)} \biggr] </math> <math>~\Rightarrow</math> <math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3} \, .</math>

For the core we have,

<math>~ (1 - \eta^2)\frac{d^2x}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} + \mathfrak{F}_\mathrm{core} x \, , </math>

where,

<math>~\eta \equiv \frac{\xi}{g} \, ,</math> and <math>~\mathfrak{F}_\mathrm{core} \equiv \frac{3\omega_\mathrm{core}^2}{2\pi G\gamma_c \rho_c} - 2\alpha_c\, .</math>

And, for the envelope we have,

<math>~ ( 1 - q^3 \xi^3 ) \frac{d^2x}{d\xi^2} + ( 3 - 6q^3 \xi^3 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e \biggr]\frac{x}{\xi^2} \, , </math>

where,

<math>~\mathfrak{F}_\mathrm{env}</math>

<math>~\equiv</math>

<math>~\frac{3\omega^2_\mathrm{env}}{2\pi G \gamma_e \rho_e} - 2\alpha_e \, . </math>

Initial Focus

Properties of 21Analytic Solution

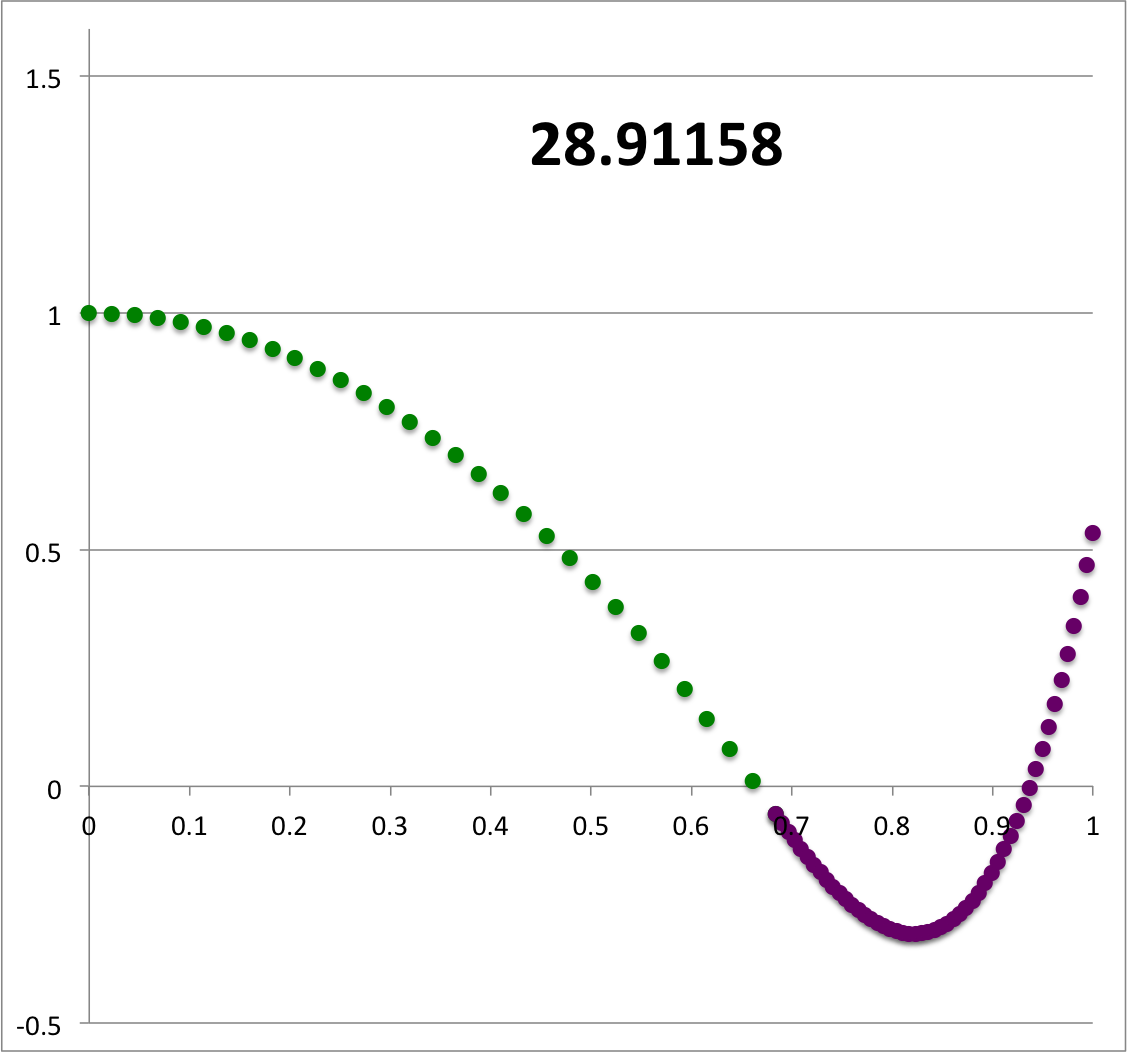
Figure 1

Same analytic, <math>~(\ell,j) = (2,1)</math> eigenfunction as here, but renormalized to unity at the center; numerical label provides value of <math>~\sigma_c^2</math>.

Evidently, one analytic solution with quantum numbers, <math>~(\ell,j) = (2,1)</math>, shown again here on the right, is available for a zero-zero bipolytrope that has the following properties:

<math>~q</math>	<math>~\approx</math>	<math>~0.6840119</math>
<math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3}</math>	<math>~\approx</math>	<math>~0.3902664</math>
<math>~\gamma_e = \frac{4}{3+0.35}</math>	<math>~\approx</math>	<math>~1.1940299</math>
<math>~\gamma_c </math>	<math>~\approx</math>	<math>~1.845579</math>
<math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G \rho_c} = 20\gamma_c - 8 </math>	<math>~\approx</math>	<math>~28.91158 \, .</math>

This means, as well, that,

<math>~c_0 \equiv \sqrt{1+\alpha_e} - 1</math>	<math>~=</math>	<math>~\sqrt{0.65}-1 \approx - 0.1937742</math>
<math>~g^2 \equiv \frac{1+8q^3}{(1+2q^3)^2}</math>	<math>~\approx</math>	<math>~1.3236092</math>
<math>~\mathfrak{F}_\mathrm{core} \equiv \frac{\sigma_c^2 + 8}{\gamma_c} - 6</math>	<math>~=</math>	<math>~14</math>
<math>~\mathfrak{F}_\mathrm{env} \equiv \frac{1}{\gamma_e} \biggl[ \sigma_c^2 \biggl(\frac{\rho_c}{\rho_e} \biggr) + 8\biggr]- 6</math>	<math>~=</math>	<math>~(c_0^2 + 17c_0 +66) = 62.743385</math>

In the envelope, the analytically defined eigenfunction is given by the expression,

<math>~x_{\ell=2} |_\mathrm{env}</math>

<math>~ \xi^{c_0}\biggl[ \frac{ 1 + q^3 A_{21} \xi^{3} + q^6 A_{21}B_{21}\xi^{6} }{ 1 + q^3 A_{21} + q^6 A_{21}B_{21}}\biggr] \, , </math>

where,

<math>~A_{21}</math>	<math>~\equiv</math>	<math>~-\biggl( \frac{ 4c_0 + 22}{2c_0 + 5}\biggr) \approx -4.6016533 \, ,</math>
<math>~B_{21}</math>	<math>~\equiv</math>	<math>~-\biggl( \frac{c_0 + 7 }{2c_0+8}\biggr) \approx -0.8940912 \, ; </math>

and in the core, it is,

<math>~x_{j=1} |_\mathrm{core}</math>

More succinctly we have,

<math>~x_\mathrm{core}</math>

and,

<math>~a \cdot x_\mathrm{env}</math>

<math>~ \xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \, , </math>

where,

<math>~a \equiv -[ 1 + q^3 A_{21} + q^6 A_{21}B_{21}] \approx - 0.05128445 \, .</math>

Demonstrate Core Solution

This means that,

<math>~\frac{dx_\mathrm{core}}{d\xi}</math>

and,

<math>~\frac{d^2x_\mathrm{core}}{d\xi^2}</math>

Therefore, the LAWE for the core becomes,

<math>~[\mathrm{LAWE}]_\mathrm{core}</math>	<math>~=</math>	<math>~ (1 - \eta^2)\frac{d^2x_\mathrm{core}}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx_\mathrm{core}}{d\eta} + \mathfrak{F}_\mathrm{core} x_\mathrm{core} </math>
	<math>~=</math>	<math>~ (g^2 - \xi^2)\frac{d^2x_\mathrm{core}}{d\xi^2} + ( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx_\mathrm{core}}{d\xi} + \mathfrak{F}_\mathrm{core} x_\mathrm{core} </math>
	<math>~=</math>	<math>~ 36.65364(1.3236092 - \xi^2) + 36.65364( 5.2944368 - 6\xi^2 ) + 14( -17.326820 + 18.326820~\xi^2) </math>
	<math>~=</math>	<math>~ 36.65364(1.3236092 ) + 36.65364( 5.2944368 ) + 14( -17.326820 ) + [36.65364(-1) + 36.65364( - 6 ) + 14( 18.326820)]\xi^2 </math>
	<math>~=</math>	<math>~ 36.65364(6.618046 ) - 14( 17.326820 ) + 36.65364 [-1 - 6 + 7]\xi^2 </math>
	<math>~=</math>	<math>~ 0 \, . </math>

Q.E.D.

Demonstrate Envelope Solution

Given that,

<math>~a\cdot x_\mathrm{env}</math>

<math>~ \xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \, , </math>

we deduce that,

<math>~a\cdot \frac{dx_\mathrm{env}}{d\xi}</math>

<math>~ -0.1937742~ \xi^{- 1.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] + \xi^{- 0.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] \, , </math>

and,

<math>~a \cdot \frac{d^2x_\mathrm{env}}{d\xi^2}</math>	<math>~=</math>	<math>~ 0.2313226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] - 2 \times 0.1937742~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math>
		<math>~ + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] \, . </math>

Therefore, the LAWE for the envelope becomes,

<math>~a\cdot [\mathrm{LAWE}]_\mathrm{env}</math>	<math>~=</math>	<math>~ a( 1 - q^3 \xi^3 ) \frac{d^2x}{d\xi^2} + a( 3 - 6q^3 \xi^3 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + a\biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e \biggr]\frac{x}{\xi^2} \, , </math>
	<math>~=</math>	<math>~ a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{3}{\xi} \cdot \frac{dx}{d\xi} -\alpha_e \biggl(\frac{x}{\xi^2} \biggr) \biggr\} - a q^3 \xi^3 \biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} - \mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr)\biggr\} \, . </math>

Now, the first of these sub-expressions gives,

<math>~ a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{3}{\xi} \cdot \frac{dx}{d\xi} -\alpha_e \biggl(\frac{x}{\xi^2} \biggr) \biggr\} </math>	<math>~=</math>	<math>~ 0.2313226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] - 2 \times 0.1937742~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math>
		<math>~ + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math>
		<math>~ -0.5813226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] + 3\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math>
		<math>~+0.35 \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math>
	<math>~=</math>	<math>~ (0.2313226 -0.5813226 + 0.35) ~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math>
		<math>~ + (3 - 2 \times 0.1937742)~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math>
	<math>~=</math>	<math>~ (3 - 2 \times 0.1937742)~ \xi^{- 2.1937742}\biggl[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} \biggr] + \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] </math>
	<math>~=</math>	<math>~ \xi^{- 2.1937742}\biggl[ -20.37783~ \xi^3 + 19.24657~\xi^{6} \biggr] </math>

And the sub-expression inside the second set of curly braces gives,

<math>~ a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} -\mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr) \biggr\} </math>	<math>~=</math>	<math>~ 0.2313226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] - 2 \times 0.1937742~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math>
		<math>~ + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math>
		<math>~ -1.1626452~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] + 6\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math>
		<math>~- 62.74339 \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math>
	<math>~=</math>	<math>~ (0.2313226 -1.1626452 - 62.74339)~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math>
		<math>~ + (6- 2 \times 0.1937742)~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math>
	<math>~=</math>	<math>~ -63.67471~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math>
		<math>~ + 5.612452~ \xi^{- 2.1937742}\biggl[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} \biggr] + \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] </math>
	<math>~=</math>	<math>~ \xi^{- 2.1937742}\biggl[ -63.67471 + 93.77171~ \xi^{3} -26.83148~\xi^{6} \biggr] </math>
		<math>~ + ~ \xi^{- 2.1937742}\biggl[ - 24.79584~ \xi^{3} + 14.18997~\xi^{6} \biggr] + \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] </math>
	<math>~=</math>	<math>~ \xi^{- 2.1937742}\biggl[ -63.67471 + (93.77171-24.79584- 8.8360086) ~ \xi^{3} + (-26.83148+14.18997 + 12.641508)~\xi^{6} \biggr] </math>
	<math>~=</math>	<math>~ \xi^{- 2.1937742}\biggl[ -63.67471 + 60.13986 ~ \xi^{3} \biggr] </math>
<math>~\Rightarrow~~~ a(q^3\xi^3) \biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} -\mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr) \biggr\} </math>	<math>~=</math>	<math>~ \xi^{- 2.1937742}\biggl[ -20.37783 +19.24657 ~ \xi^{6} \biggr] \, . </math>

But these two sub-expressions cancel precisely, which means that our eigenfunction satisfies the LAWE! Q.E.D.

Boundary Conditions

Notice that for this particular eigenfunction solution, the value and first radial derivative at the center <math>~(\xi=0)</math> of the configuration is,

<math>~x_\mathrm{core}</math>

<math>~-17.326820 + 18.326820~\cancelto{0}{\xi^2} = -17.326820 \, ;</math>

and,

<math>~\frac{dx_\mathrm{core}}{d\xi}</math>

<math>~36.65364~\cancelto{0}{\xi} = 0 \, .</math>

And, at the surface <math>~(\xi = q^{-1}) </math> the value and first radial derivative are,

<math>~a \cdot x_\mathrm{env}</math>	<math>~=</math>	<math>~ \biggl\{\xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \biggr\}_{\xi=1/q} </math>
	<math>~\approx</math>	<math>~ 0.47627246\, , </math>

where,

<math>~a \approx - 0.05128445 \, ;</math>

and,

<math>~\frac{d\ln x_\mathrm{env}}{d\ln \xi} </math>	<math>~=</math>	<math>~ \frac{\xi}{a\cdot x_\mathrm{env}} \biggl[ a\cdot \frac{dx_\mathrm{env}}{d\xi} \biggr]</math>
	<math>~=</math>	<math>~ \frac{ -0.1937742~\xi^{- 0.1937742}[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] + \xi^{- 0.1937742}[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{\xi^{- 0.1937742} [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } </math>
	<math>~=</math>	<math>~ -0.1937742 + \frac{~ [ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{ [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } </math>
<math>~\Rightarrow ~~~ \biggl\{ \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr\}_{\xi=1/q} </math>	<math>~=</math>	<math>~ -0.1937742 + \biggl\{ \frac{[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{ [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } \biggr\}_{\xi=1/q} </math>
	<math>~=</math>	<math>~ -0.1937742 + 21.22492 = 21.03115 \, . </math>

Finite-Difference Representation

General Approach

Working with the Taylor series expansion, we can write,

<math>~\approx</math>

<math>~ x(a) + (\xi - a) x_a' + \tfrac{1}{2} (\xi-a)^2 x_a \, , </math>

and letting <math>~\xi_\pm = a \pm \Delta </math>, we have,

<math>~\approx</math>

<math>~ x(a) + \Delta \cdot x_a' + \tfrac{1}{2} \Delta^2 x_a \, , </math>

and,

<math>~\approx</math>

<math>~ x(a) - \Delta \cdot x_a' + \tfrac{1}{2} \Delta^2 x_a \, . </math>

Subtracting the second of these two expressions from the first gives,

<math>~x_+ - x_-</math>	<math>~\approx</math>	<math>~ 2 \Delta \cdot x_a' </math>
<math>~\Rightarrow ~~~ x_a'</math>	<math>~\approx</math>	<math>~ \frac{x_+ - x_-}{2 \Delta} \, ; </math>

while, adding the two expressions together gives,

<math>~\frac{x_+ - 2x_a + x_-}{\Delta^2}</math>

<math>~\approx</math>

Integrating Outward Through the Core

From the LAWE for the core, we have,

<math>~ - ( 4g^2 - 6a^2 ) x_a' - a \mathfrak{F}_\mathrm{core} x_a \, . </math>

So, putting these last three expressions together gives an approximate relation between <math>~x_+</math> and the previous two values of the function, <math>~x_-</math> and <math>~x_a</math>, namely,

<math>~a (g^2 - a^2) \biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr]</math>	<math>~\approx</math>	<math>~ - ( 4g^2 - 6a^2 ) \biggl[\frac{x_+ - x_-}{2 \Delta} \biggr] - a \mathfrak{F}_\mathrm{core} x_a </math>
<math>~\Rightarrow~~~ a (g^2 - a^2) \biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 4g^2 - 6a^2 ) \biggl[\frac{x_+ }{2 \Delta} \biggr] </math>	<math>~\approx</math>	<math>~a (g^2 - a^2) \biggl[ \frac{2x_a - x_-}{\Delta^2} \biggr] + ( 4g^2 - 6a^2 ) \biggl[\frac{x_-}{2 \Delta} \biggr] - a \mathfrak{F}_\mathrm{core} x_a </math>
<math>~ \Rightarrow~~~x_+[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) ] </math>	<math>~\approx</math>	<math>~2a (g^2 - a^2) [ 2x_a - x_- ] + ( 4g^2 - 6a^2 ) [\Delta x_- ] - 2\Delta^2 a \mathfrak{F}_\mathrm{core} x_a </math>
	<math>~\approx</math>	<math>~[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a + [ \Delta( 4g^2 - 6a^2 ) - 2a (g^2 - a^2)] x_- \, . </math>

Now, at the very center of the configuration, <math>~(a = 0)</math>, we expect the function, <math>~x(\xi)</math>, to be symmetric; that is, we expect <math>~x_- = x_+</math>. So for this case alone, we have,

<math>~ x_+[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) - \Delta( 4g^2 - 6a^2 ) + 2a (g^2 - a^2)] </math>	<math>~=</math>	<math>~[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a </math>
<math>~\Rightarrow~~~ x_+[2(g^2 - \cancelto{0}{a^2}) + 2(g^2 - \cancelto{0}{a^2})] </math>	<math>~=</math>	<math>~[4 (g^2 - \cancelto{0}{a^2}) - 2\Delta^2 \mathfrak{F}_\mathrm{core} ]x_a </math>
<math>~\Rightarrow~~~ x_+ </math>	<math>~=</math>	<math>~\biggl[ 1 - \frac{\Delta^2 \mathfrak{F}_\mathrm{core}}{2g^2} \biggr]x_a \, . </math>

For all other coordinate locations, <math>~a = \xi</math>, in the range, <math>~0 < \xi < 1</math>, we will use the general expression, namely,

<math>~ \Rightarrow~~~x_+ </math>

<math>~\approx</math>

<math>~\frac{[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a + [ \Delta( 4g^2 - 6a^2 ) - 2a (g^2 - a^2)] x_- }{[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) ] } \, . </math>

Keep in mind that, when we move across the interface at <math>~a = 1</math>, we want both the value of the function, <math>~x_q</math>, and its first derivative, <math>~x_q'</math>, to be the same as viewed from both the envelope and the core. In a numerical integration algorithm, it will be very straightforward to set the value of the eigenfunction at the interface. In order to properly handle the first derivative, I propose that we extend the core solution and evaluate the eigenfunction at one zone beyond the interface, and identify the values of the eigenfunction that straddles the interface as,

<math>~(x_-)_q</math> and <math>~(x_+)_q</math>.

Then define the slope of the eigenfunction at the interface by the expression,

Slope at the Interface

<math>~\equiv</math>

<math>~\frac{(x_+)_q - (x_-)_q}{2\Delta} \, .</math>

Integrating Outward Through the Envelope

From the LAWE for the envelope, we have,

<math>~ - ( 3 - 6q^3 a^3 ) a x_a' - [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a \, . </math>

Inserting the same finite-difference expressions for the first and second derivatives, we therefore have,

<math>~a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr] </math>	<math>~=</math>	<math>~ - ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_+ - x_-}{2 \Delta} \biggr] - [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a </math>
<math>~\Rightarrow ~~~ a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_+ }{2 \Delta} \biggr] </math>	<math>~=</math>	<math>~ ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_-}{2 \Delta} \biggr] - a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_- - 2x_a }{\Delta^2} \biggr] - [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a </math>
<math>~\Rightarrow ~~~ x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a ] </math>	<math>~=</math>	<math>~ [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] x_- + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math>

Now, at the interface (only), we need to relate <math>~x_-</math> to <math>~x_+</math> in such a way that the slope gives the proper value at the interface. Specifically, we need to set,

<math>~x_+ - 2\Delta (x_q') \, ,</math>

where, <math>~x_q'</math> takes the value that was determined for the core. Hence, at the interface <math>~(a = 1)</math>, the first step into the envelope is special and demands that,

<math>~ x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a ] </math>	<math>~=</math>	<math>~ [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] [x_+ - 2\Delta (x_q')] + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math>
<math>~\Rightarrow ~~~ x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a -\Delta ( 3 - 6q^3 a^3 ) a + 2a^2( 1 - q^3 a^3 ) ] </math>	<math>~=</math>	<math>~ [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] [- 2\Delta (x_q')] + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math>
<math>~\Rightarrow ~~~ x_+ [4a^2( 1 - q^3 a^3 ) ] </math>	<math>~=</math>	<math>~ -2\Delta [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] x_q' + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math>
and, setting, <math>~a = 1 ~~~~\Rightarrow ~~~ x_+ </math>	<math>~=</math>	<math>~ \frac{ 2\Delta [2( 1 - q^3 ) - \Delta ( 3 - 6q^3 ) ] x_q' + [4( 1 - q^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} -\alpha_e ) ] x_a }{ 4( 1 - q^3 ) } \, . </math>

Varying the Oscillation Frequency

Approach

First, we fix <math>~q</math>, <math>~\gamma_e</math>, and <math>~\gamma_c</math>; in the example, here (as above) we choose: <math>~(q,\gamma_e,\gamma_c) = ( 0.6840119, 1.1940299, 1.845579)</math>. For this example, we will also retain the constraint, <math>~g^2 = \mathcal{B}</math>, in which case,

<math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3}</math>	<math>~\approx</math>	<math>~0.3902664</math>
<math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G \rho_c} = 20\gamma_c - 8 </math>	<math>~\approx</math>	<math>~28.91158 \, .</math>

Next, we pick various values of the (square of the) dimensionless oscillation frequency, <math>~\sigma_c^2</math>, and from each value we set,

<math>~\mathfrak{F}_\mathrm{core} </math>	<math>~=</math>	<math>~\frac{\sigma_c^2 + 8}{\gamma_c} - 6 \, ,</math>
<math>~\mathfrak{F}_\mathrm{env} </math>	<math>~=</math>	<math>~\frac{1}{\gamma_e} \biggl[ \sigma_c^2 \biggl(\frac{\rho_e}{\rho_c} \biggr)^{-1} + 8\biggr]- 6 \, .</math>

For the finite-difference algorithm, we divide the core — radial coordinate range, <math>~0 \le \xi \le 1</math> — into N_core zones, and the envelope — radial coordinate range, <math>~1\le \xi \le 1/q</math> — into N_env zones. This means that the spacing between successive radial zones in the core and envelope is, respectively,

<math>~\Delta_c \equiv \frac{1}{\mathrm{N}_\mathrm{core}}</math>

and

<math>~\Delta_e \equiv \frac{q^{-1} - 1}{\mathrm{N}_\mathrm{env}} \, .</math>

Starting at the center of the configuration <math>~(\xi = 0)</math>, where we arbitrarily set the value of the eigenfuntion to <math>~x_0 = 1</math>, the value of the eigenfunction at the first grid point away from the center <math>~(\xi = \Delta_c)</math> is,

<math>~\biggl[ 1 - \frac{\Delta_c^2 \mathfrak{F}_\mathrm{core}}{2g^2} \biggr]x_0 \, . </math>

Thereafter — moving out toward and just beyond the interface location <math>~(\xi = 1/q)</math>, the radial coordinate of each successive grid point is <math>~\xi_k = k\Delta_c</math>, and the numerically determined value of the eigenfunction at each successive grid point <math>~(k = 1 \rightarrow \mathrm{N}_\mathrm{core})</math> is,

<math>~\approx</math>

<math>~\frac{[4\xi_k (g^2 - \xi_k^2) - 2\Delta_c^2 \xi_k \mathfrak{F}_\mathrm{core} ]x_k + [ \Delta_c( 4g^2 - 6\xi_k^2 ) - 2\xi_k (g^2 - \xi_k^2)] x_{k-1} }{[2a (g^2 - \xi_k^2) + \Delta_c( 4g^2 - 6\xi_k^2 ) ] } \, . </math>

Then, at the interface, which is associated with <math>~k = \mathrm{N}_\mathrm{core}</math>, we define the reference slope as,

<math>~\frac{x_{k+1} - x_{k-1}}{2\Delta_c} \, .</math>

Next, we move outward into the envelope, using the integer index, <math>~n = 1 \rightarrow \mathrm{N}_\mathrm{env}</math>, to label successive radial grid locations <math>~(\xi_n = 1 + n\Delta_e)</math>. Letting the value of the eigenfunction at the interface be represented by <math>~x_q</math>, at the first grid location outside the interface <math>~(\xi = 1 + \Delta_e)</math>, the value of the eigenfunction is,

<math>~ \frac{ 2\Delta_e [2( 1 - q^3 ) - \Delta_e ( 3 - 6q^3 ) ] x_q' + [4( 1 - q^3 ) - 2\Delta_e^2 ( q^3 \mathfrak{F}_\mathrm{env} -\alpha_e ) ] x_q }{ 4( 1 - q^3 ) } \, . </math>

Thereafter, moving outward through the envelope to the surface, the value of the eigenfunction at each successive grid location is,

<math>~ \frac{[ \Delta_e ( 3 - 6q^3 \xi_n^3 ) \xi_n - 2\xi_n^2( 1 - q^3 \xi_n^3 ) ] x_{n-1} + [4\xi_n^2( 1 - q^3 \xi_n^3 ) - 2\Delta_e^2 ( q^3 \mathfrak{F}_\mathrm{env} \xi_n^3 -\alpha_e ) ] x_{n} }{ [2\xi_n^2( 1 - q^3 \xi_n^3 ) + \Delta_e ( 3 - 6q^3 \xi_n^3 ) \xi_n ] } \, . </math>

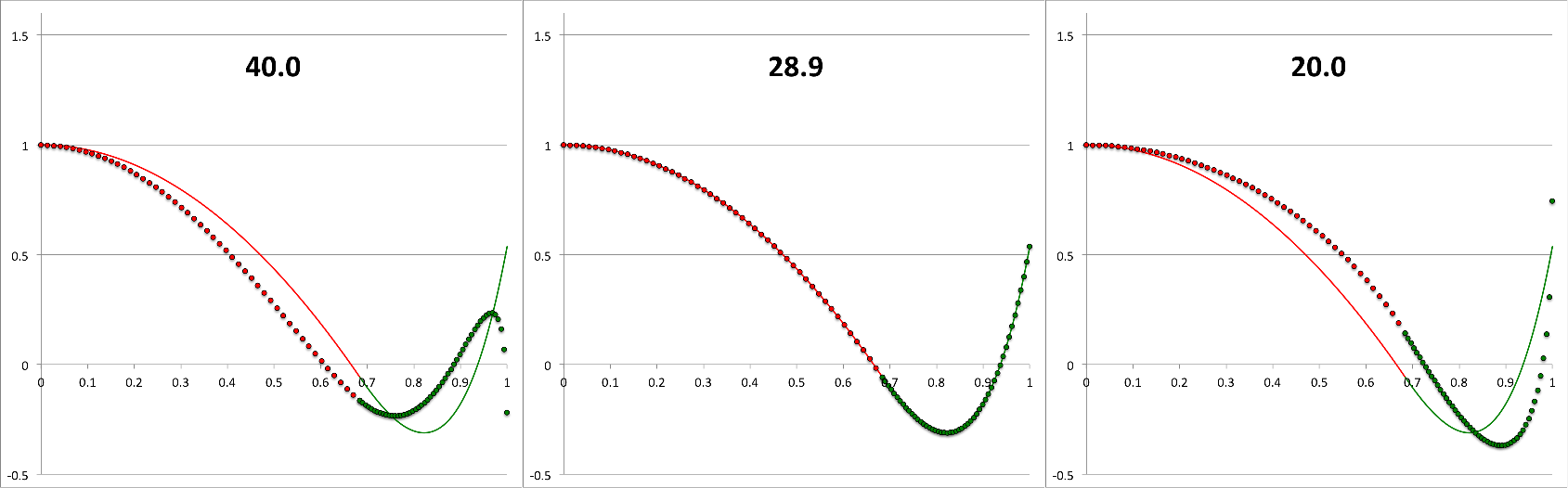
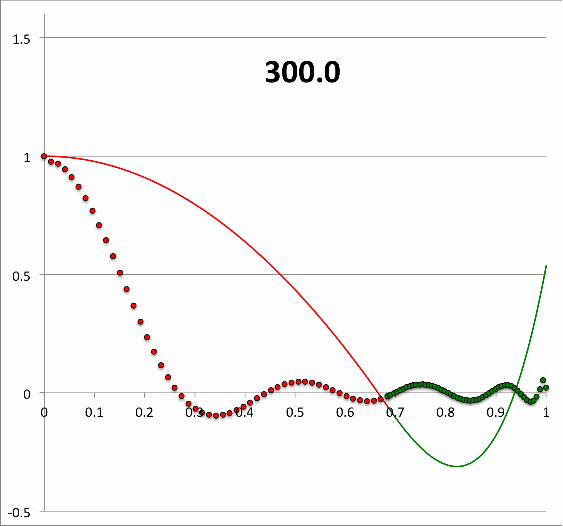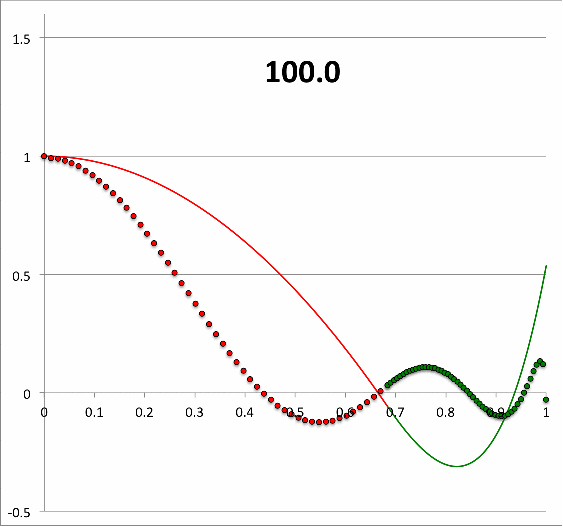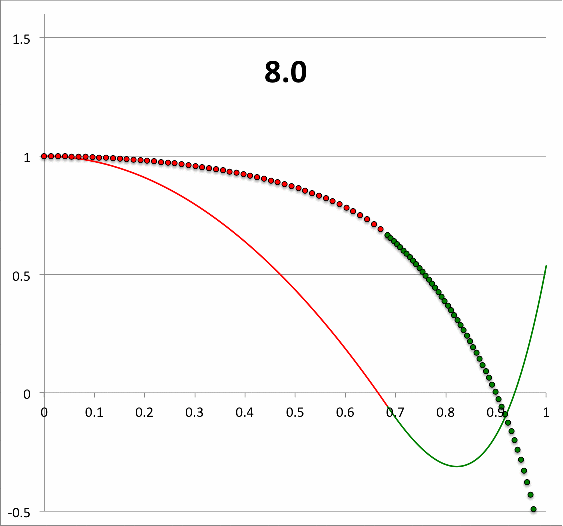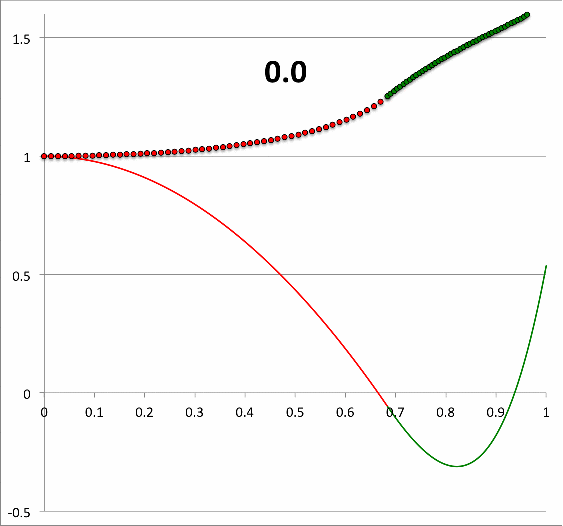
Results

User:Tohline/Appendix/Ramblings/NumericallyDeterminedEigenvectors

Contents

Numerically Determined Eigenvectors of a Zero-Zero Bipolytrope

Setup

Initial Focus

Properties of 21Analytic Solution

Demonstrate Core Solution

Demonstrate Envelope Solution

Boundary Conditions

Finite-Difference Representation

General Approach

Integrating Outward Through the Core

Integrating Outward Through the Envelope

Varying the Oscillation Frequency

Approach

Results

Navigation menu

Search