Summary for Hadley & Imamura

This MediaWiki-based document is especially provided for Jimmy Imamura and Kathryn Hadley. It summarizes the contents of a much longer set of technical notes that discusses the analysis of nonaxisymmetric distortions in rotating, self-gravitating fluids. The punchline is provided by the animation sequence shown in Figure 2, below.

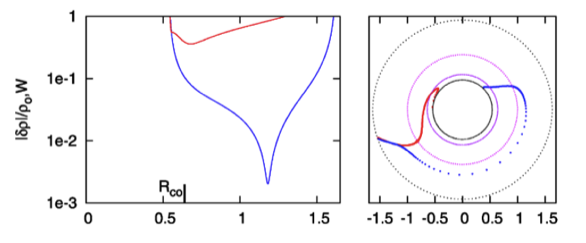
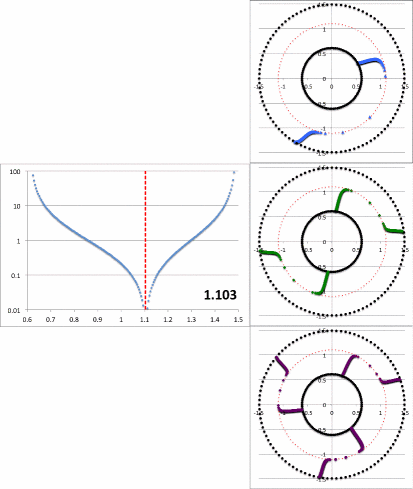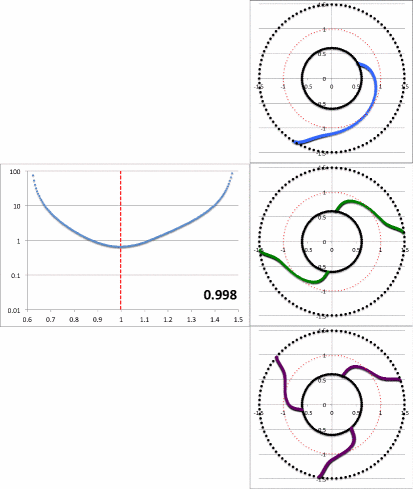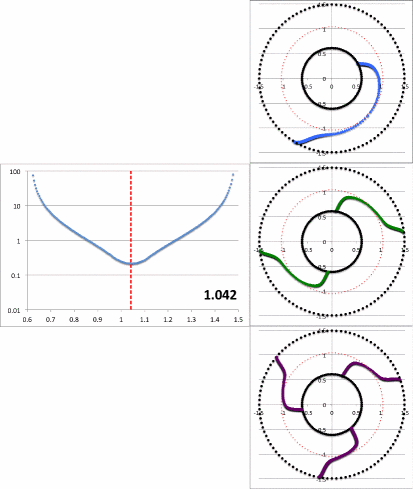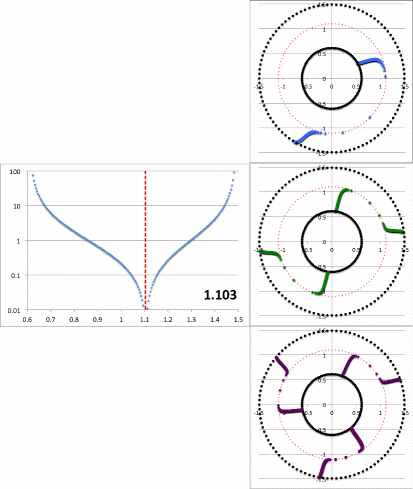
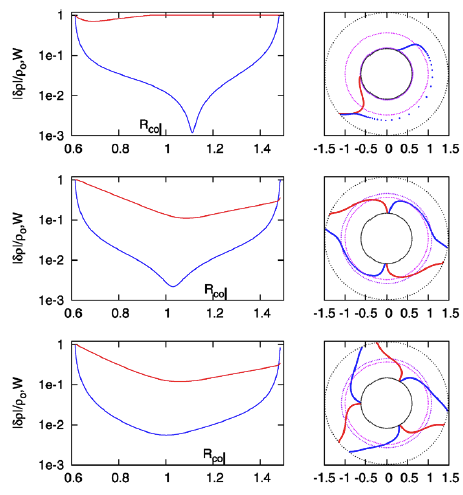
While studying the series of three papers that has recently been published by the Imamura & Hadley collaboration, I was particularly drawn to the pair of plots presented in Figure 6 — and, again, in the top portion of Figure 13 and the top portion of Figure 16 — of HI11. This pair of plots has been reprinted here, without modification, as our Figure 1. The curves delineated by the blue dots in this pair of HI11 plots display (on the left) the shape of the eigenfunction, <math>~f_1(\varpi)</math>, and (on the right) the "constant phase loci," <math>~\phi_1(\varpi)</math>, for an unstable, <math>~m=1</math> mode. In this case, the initial model for the depicted evolution is the equilibrium model from Table 2 of HI11 that has <math>~T/|W| = 0.253</math>; it is a fully self-gravitating torus with polytropic index, <math>~n = 3/2</math>, and a rotation-law profile defined by a "Keplerian" angular velocity profile.

Figure 1

Panel pair extracted^† without modification from the top-most segment of Figure 13, p. 18 of K. Hadley & J. N. Imamura (2011)

"Nonaxisymmetric Instabilities of Self-Gravitating Disks. I Toroids"

Astrophysics and Space Science, 334, 1 - 26 © Springer Science+Business Media B.V.

^†This pair of plots also appears in the top portion of Figure 16 on p. 20 and, by itself, as Figure 6 on p. 12 of K. Hadley & J. N. Imamura (2011).

Radial Eigenfunction

It occurred to me, first, that the blue curve displayed in the left-hand panel of Figure 1 might be reasonably well approximated by piecing together a pair of arc-hyperbolic-tangent (ATANH) functions. In an effort to demonstrate this, I began by specifying a "midway" radial location, <math>~r_- < r_\mathrm{mid} < r_+ \, ,</math> at which the two ATANH functions meet and at which the density fluctuation is smallest. Then I defined a function of the form,

	<math>~f_\ln(\varpi)</math>	<math>~=</math>	<math>~\tanh^{-1}\biggl[1 - 2 \biggl( \frac{\varpi - r_-}{r_\mathrm{mid}-r_-} \biggr) \biggr]</math>	for	<math>r_- < \varpi < r_\mathrm{mid} \, ;</math>
and
	<math>~f_\ln(\varpi)</math>	<math>~=</math>	<math>~\tanh^{-1}\biggl[1 - 2 \biggl( \frac{\varpi - r_+}{r_\mathrm{mid}-r_+} \biggr) \biggr]</math>	for	<math>r_\mathrm{mid} < \varpi < r_+ \, .</math>

Recognizing that the figure depicting the HI11 eigenfunction is a semi-log plot, it seems clear that the relationship between our constructed function, <math>~f_\ln(\varpi)</math>, and the eigenfunction, <math>~f_1(\varpi)</math>, is,

<math>~f_1(\varpi) = e^{f_\ln(\varpi)} \, .</math>

Given that, in general, the following mathematical relation holds,

<math>~\ln\biggl( \frac{1+x}{1-x} \biggr)^{1/2} </math>

for

we can write for the innermost region of the toroidal configuration — that is, over the lower radial-coordinate range —

<math>~f_1(\varpi) = e^{f_\ln(\varpi)}</math>

<math>~\biggl( \frac{r_\mathrm{mid} - \varpi}{\varpi - r_-} \biggr)^{1/2} </math>

for

Similarly, we find that, over the upper radial-coordinate range,

<math>~f_1(\varpi) = e^{f_\ln(\varpi)}</math>

<math>~\biggl( \frac{r_\mathrm{mid} - \varpi}{\varpi - r_+} \biggr)^{1/2} </math>

for

<math>r_\mathrm{mid} < \varpi < r_+ \, .</math>

After a bit more experimentation, we recognized that it is advantageous to replace the square root — that is, the exponent, ½ — with a variable exponent, <math>~p</math>, that can serve as an adjustable fitting parameter; and, in order to facilitate a degree of radial overlap between the two ATANH functions, we introduced different values of <math>~r_\mathrm{mid}</math> on the left and on the right. This led to a two-piece radial eigenfunction of the form,

<math>~f_\mathrm{blue}(\varpi) </math>

<math>~\biggl( \frac{r_\mathrm{blue} - \varpi}{\varpi - r_-} \biggr)^{p} </math>

for

and,

<math>~f_\mathrm{green}(\varpi) </math>

<math>~\biggl( \frac{r_\mathrm{green} - \varpi}{\varpi - r_+} \biggr)^{p} </math>

for

<math>r_\mathrm{green} < \varpi < r_+ \, ,</math>

where, <math>~r_\mathrm{mid}|_\mathrm{green} \le r_\mathrm{mid}|_\mathrm{blue}</math>. The expression that we are currently using for the radial eigenfunction is a sum of these two pieces, that is,

<math>~f_1(\varpi)</math>

<math>~f_\mathrm{green}(\varpi) + f_\mathrm{blue}(\varpi) \, . </math>

For later use, we define from this function the minimum and maximum values,

<math>~[f_\ln]_\mathrm{min} \equiv \mathrm{min}[\ln(f_1)]</math>

and

<math>~[f_\ln]_\mathrm{max} \equiv \mathrm{max}[\ln(f_1)] \, .</math>

Constant Phase Loci

As is explained in our accompanying detailed technical notes — see, also another improvement — we have settled on the following prescription for the phase function, <math>~\phi_m(\varpi)</math>:

<math>~\tan^{-1}[\aleph \cdot D_{1/2}(\varpi)] \, .</math>

where, <math>~\aleph</math> is a constant to be specified,

<math>~D_{1/2}(\varpi)</math>

<math>~\equiv</math>

<math>~\biggl[ \frac{f_\ln(\varpi) - [f_\ln]_\mathrm{min}}{[f_\ln]_\mathrm{max} - [f_\ln]_\mathrm{min}} \biggr]^{1/2} \, ,</math>

and,

<math>~f_\ln(\varpi)</math>

<math>~\equiv</math>

<math>~\ln[ f_1(\varpi)] \, .</math>

Put It Together

Figure 2: Radial and Azimuthal Eigenfunction Comparison
(a) Our Empirically Constructed Function	(b) Extracted from Figure 16 of HI11

User:Tohline/Appendix/Ramblings/To Hadley and Imamura

Contents

Summary for Hadley & Imamura

Radial Eigenfunction

Constant Phase Loci

Put It Together

See Also

Navigation menu

Search