User:Tohline/Appendix/Ramblings/To Hadley and Imamura
Summary for Hadley & Imamura

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
In what follows, we will draw heavily from three publications: (1) J. E. Tohline & I. Hachisu (1990, ApJ, 361, 394-407) — hereafter, TH90 — (2) J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247-267) — hereafter, WTH94 — and (3) K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1) — hereafter, HI11.
Another Improvement
I've realized that the phase plot is much smoother — in particular, the derivatives of both segments appear to match at their point of intersection — if we use <math>~D^{1/2}</math>, instead of simply <math>~D</math>, as the argument of the arctangent function. So, we define,
|
<math>~D_{1/2}(\varpi)</math> |
<math>~\equiv</math> |
<math>~\sqrt{D(\varpi)} = \biggl[ \frac{f_\ln(\varpi) - [f_\ln]_\mathrm{min}}{[f_\ln]_\mathrm{max} - [f_\ln]_\mathrm{min}} \biggr]^{1/2} \, ,</math> |
and henceforward will set,
|
<math>~m\phi_m</math> |
<math>~=</math> |
<math>~\tan^{-1}[\aleph \cdot D_{1/2}(\varpi)] \, .</math> |
|
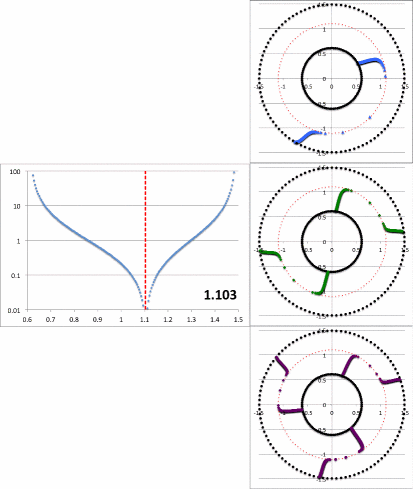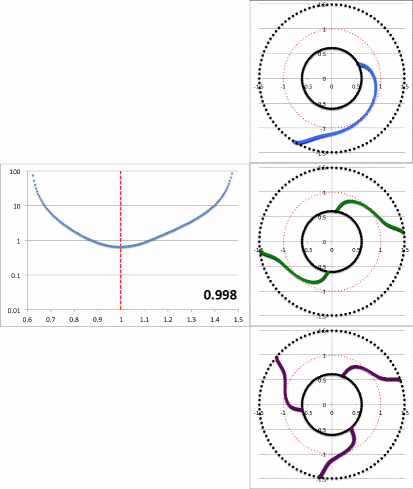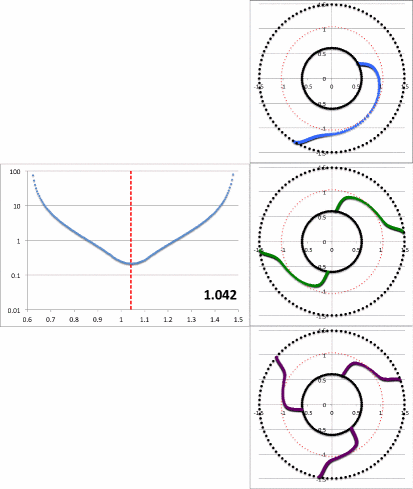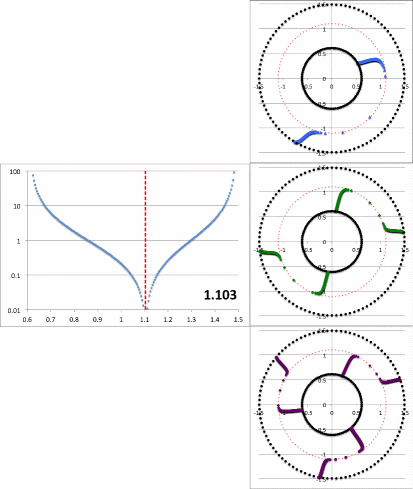
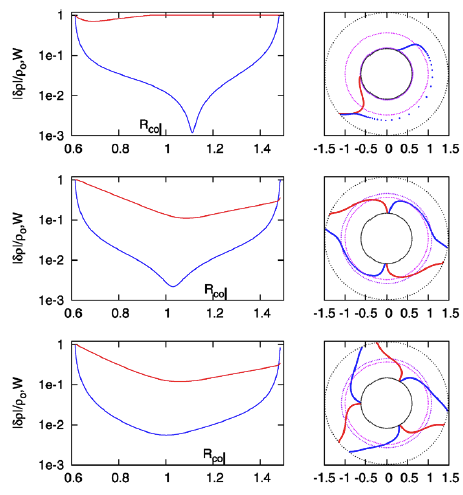
Figure 8: Radial and Azimuthal Eigenfunction Comparison |
|
| (a) Our Empirically Constructed Function | (b) Extracted from Figure 16 of HI11 |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |