Reconciling Eulerian versus Lagrangian Perspectives

Introduction

In an accompanying discussion, we have reviewed T. E. Sterne's (1937, MNRAS, 97, 582) study of radial pulsation modes in the homogeneous sphere. He solved the eigenvalue problem as defined by the

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

and, hence, as established via a Lagrangian formulation of the problem. The eigenvectors and eigenvalues that Sterne derived for the first two or three radial modes have also appeared — usually in the context of separate, re-derivations — in other publications: See, for example, §38.2 (pp. 402-403) of [KW94].

After finishing that review, we became aware that a separate study of radial pulsation modes in the homogeneous sphere has been published by S. Rosseland (1969) In his book titled, The Pulsation Theory of Variable Stars (see, specifically his § 3.2, beginning on p. 27). Rosseland solved an eigenvalue problem as defined by the relation,

<math>~\frac{\partial}{\partial r} \biggl( \gamma P_0 \nabla\cdot \vec{\xi}\biggr) + \biggl( \omega^2 + \frac{4g_0}{r}\biggr) \rho_0 \xi</math>

(see his equation 2.23 on p. 20, with the adiabatic condition being enforced by setting the right-hand-side equal to zero), where,

<math>~\vec\xi = \mathbf{\hat{e}}_r \xi(r) \, .</math>

Rosseland derived this expression in an earlier section of his book via an Eulerian formulation of the problem. Realizing that, for a spherically symmetric system,

<math>\nabla\cdot \vec\xi = \frac{1}{r^2}\frac{\partial}{\partial r}\biggl(r^2 \xi\biggr) = \frac{\partial \xi}{\partial r} + \frac{2\xi}{r} \, ,</math>

as is demonstrated in and accompanying discussion, this relation can be rewritten in the more familiar form of a 2^nd-order ODE, namely,

<math>~P_0 \frac{\partial^2 \xi}{\partial r^2} + \biggl[ \frac{2P_0}{r}- \rho_0 g_0 \biggr] \frac{\partial \xi}{\partial r} + \biggl[ \biggl( \frac{\omega^2\rho_c}{\gamma} + \frac{4\rho_c g_0}{\gamma r}\biggr) \biggl(\frac{\rho_0}{\rho_c}\biggr) - \biggl(\frac{2\rho_c g_0 }{r}\biggr)\biggl(\frac{\rho_0}{\rho_c}\biggr) - \frac{2P_0}{r^2} \biggr] \xi </math>

Here we will repeat the setup and solution of both eigenvalue problems in an effort to reconcile differences. As we have explained elsewhere, an equilibrium, homogeneous, self-gravitating sphere has the following structural properties:

<math> \frac{g_0}{g_\mathrm{SSC}} = 2\chi_0 \, , </math>

where,

<math>P_c = \frac{3G}{8\pi}\biggl( \frac{M^2}{R^4} \biggr) </math> and <math>\rho_c = \frac{3M}{4\pi R^3} \, ,</math>

and the characteristic gravitational acceleration is defined as,

<math> g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} \, . </math>

In addition, it will be useful to recognize that the square of the characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) is,

<math> \tau_\mathrm{SSC}^2 \equiv \frac{R^2 \rho_c}{P_c} = \frac{2R^3}{G M} \, . </math>

Lagrangian Reformulation

Quite generally, we can rewrite the Lagrangian-formulated wave equation as,

<math> \biggl(\frac{P_0}{P_c}\biggr)\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0}\biggl(\frac{P_0}{P_c}\biggr) - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 . </math>

Note that we are convinced that this expression is error-free because, for example, when the structural properties of an equilibrium, <math>~n=1</math> polytrope are plugged into it, as is demonstrated in an accompanying discussion, we obtain exactly the same 2^nd-order ODE as published by Murphy & Fiedler (1985). For an homogeneous sphere, in particular, this expression can be rewritten as follows.

<math>~0</math>	<math>~=</math>	<math>~ ( 1-\chi_0^2 )\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4(1-\chi_0^2)}{\chi_0} - 2\chi_0 \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl[2\biggl(\frac{\omega^2 R^3}{GM}\biggr) + 2(4 - 3\gamma_\mathrm{g}) \biggr] x </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 )\frac{d^2x}{d\chi_0^2} + \frac{1}{\chi_0}\biggl[4 - 6\chi_0^2 \biggr] \frac{dx}{d\chi_0} + \mathfrak{F} x \, , </math>

where,

<math>~\mathfrak{F} \equiv \frac{2}{\gamma_\mathrm{g}} \biggl[\biggl(\frac{\omega^2 R^3}{GM}\biggr) + (4 - 3\gamma_\mathrm{g}) \biggr] \, .</math>

This expression precisely matches equation (2) of Sterne (1937).

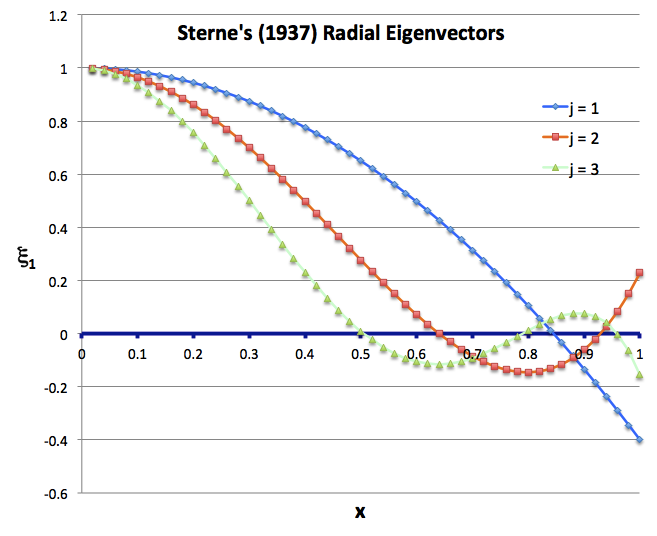
Drawing from Sterne's presentation, the following table details the eigenfunctions for the four lowest radial modes that satisfy this wave equation.

Sterne's (1937) Eigenfunctions for Homogeneous Sphere
Mode	Eigenvector	Square of Eigenfrequency: <math>~3\omega^2/(4\pi G\rho)</math>
<math>~j</math>	Eigenvector	<math>~\gamma[3+j(2j+5)] - 4</math>
<math>~0</math>	<math>~x = 1</math>	<math>~3\gamma-4</math>
<math>~1</math>	<math>~x = 1 -\frac{7}{5} \chi_0^2</math>	<math>~10\gamma-4</math>
<math>~2</math>	<math>~x = 1 -\frac{18}{5} \chi_0^2 + \frac{99}{35} \chi_0^4</math>	<math>~21\gamma-4</math>
<math>~3</math>	<math>~x = 1 -\frac{33}{5} \chi_0^2 + \frac{429}{35} \chi_0^4 - \frac{143}{21} \chi_0^6</math>	<math>~36\gamma-4</math>

Eulerian Reformulation

Using the same characteristic time scale and gravitational acceleration, we can similarly rewrite the Eulerian-formulated expression as,

<math>~ \biggl(\frac{P_0}{P_c}\biggr) \frac{\partial^2 \xi}{\partial \chi_0^2} + \biggl[ \frac{2}{\chi_0}\biggl(\frac{P_0}{P_c}\biggr) - \frac{g_0 }{g_\mathrm{SSC}}\biggl(\frac{\rho_0}{\rho_c}\biggr) \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \biggl[\frac{\omega^2\tau_\mathrm{SSC}^2}{\gamma} + \frac{2}{\chi_0 } \biggl(\frac{2}{\gamma } - 1\biggr)\frac{g_0}{g_\mathrm{SSC}}\biggr] \biggl(\frac{\rho_0}{\rho_c}\biggr) - \frac{2}{\chi_0^2} \biggl(\frac{P_0}{P_c}\biggr) \biggr\} \xi </math>

Note that we are convinced that this expression is error-free because, for example, when the structural properties of an equilibrium, "linear stellar model" are plugged into it, we obtain exactly the same 2^nd-order ODE as published by R. Stothers & J. A. Frogel (1967, ApJ, 148, 305) — see their equation (2). For an homogeneous sphere, in particular, this expression can be rewritten as follows.

<math>~0</math>	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \biggl[ \frac{2( 1-\chi_0^2 )}{\chi_0} - 2\chi_0\biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \frac{1}{\gamma}\biggl[2\biggl( \frac{\omega^2 R^3}{GM} \biggr) + 4\biggl(2 - \gamma\biggr) \biggr] - \frac{2}{\chi_0^2} ( 1-\chi_0^2 ) \biggr\} \xi </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{1}{\chi_0}\biggl[ 2 - 4\chi_0^2\biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \frac{2}{\gamma}\biggl[\biggl( \frac{\omega^2 R^3}{GM} \biggr) + \biggl(4 - 3\gamma\biggr) +\gamma\biggr] - \frac{2}{\chi_0^2} ( 1-\chi_0^2 ) \biggr\} \xi </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{1}{\chi_0}\biggl[ 4 - 6\chi_0^2 - 2(1-\chi_0^2) \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \mathfrak{F} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \biggr\} \xi \, . </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{1}{\chi_0}\biggl[ 4 - 6\chi_0^2 \biggr] \frac{\partial \xi}{\partial \chi_0} + \mathfrak{F} \xi - \frac{1}{\chi_0}\biggl[ 2(1-\chi_0^2) \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \xi </math>

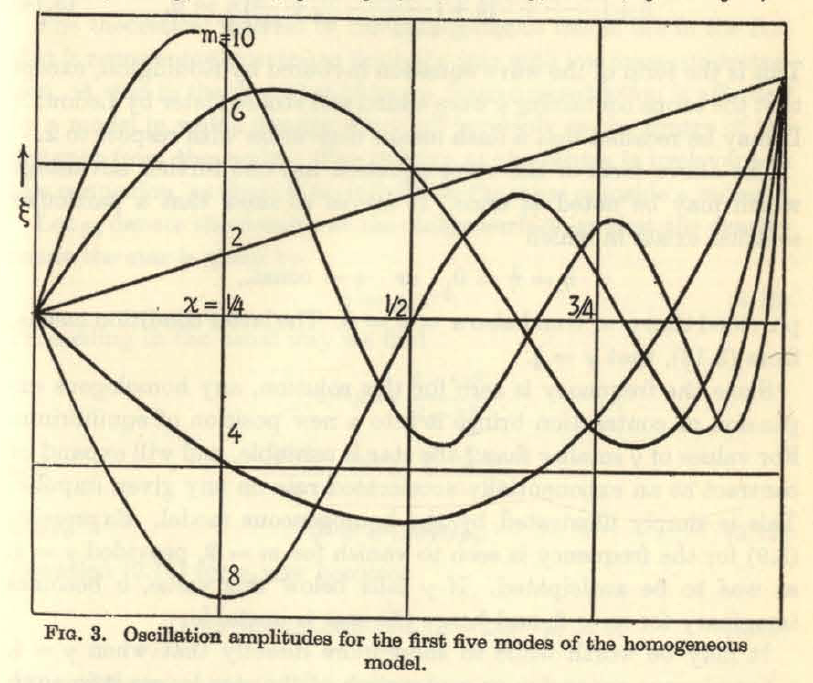
Drawing from Rosseland's presentation (see his p. 29), the following table details the eigenfunctions for the three lowest radial modes that satisfy this wave equation.

Rosseland's (1964) Eigenfunctions for Homogeneous Sphere Figure in the right-most column extracted from p. 29 of Rosseland (1964) "The Pulsation Theory of Variable Stars" (New York: Dover Publications, Inc.)
Mode	Eigenvector		Square of Eigenfrequency: <math>~3\sigma^2/(4\pi G\rho)</math>
<math>~m</math>	As Published	Rewritten	<math>~\frac{m}{2}(m+1)\gamma - 4</math>
<math>~2</math>	<math>~\xi = -2\chi_0</math>	<math>~-\frac{1}{2}\biggl( \frac{\xi}{\chi_0}\biggr) = 1</math>	<math>~3\gamma - 4</math>
<math>~4</math>	<math>~\xi = -\frac{20}{3}\chi_0 + \frac{28}{3}\chi_0^3</math>	<math>~-\frac{3}{20}\biggl( \frac{\xi}{\chi_0}\biggr) = 1- \frac{7}{5}\chi_0^2</math>	<math>~10\gamma-4</math>
<math>~6</math>	<math>~\xi = -14\chi_0 + \frac{252}{5} \chi_0^3 - \frac{198}{5} \chi_0^5</math>	<math>~-\frac{1}{14}\biggl( \frac{\xi}{\chi_0}\biggr) = 1 - \frac{18}{5} \chi_0^2 + \frac{99}{35} \chi_0^4</math>	<math>~21\gamma-4</math>

Reconciliation by Rosseland

Rosseland (1969) points out that these two different formulations can be reconciled by adopting the following dependent coordinate substitution (see his equation 3.11):

<math>~x \rightarrow \frac{\xi}{\chi_0} \, .</math>

This means that the derivatives that appear in the above Lagrangian formulation should be replaced by the expressions,

<math>~\frac{dx}{d\chi_0} \rightarrow \biggl(\frac{1}{\chi_0}\biggr)\frac{d\xi}{d\chi_0} - \frac{\xi}{\chi_0^2} \, ,</math>

and,

<math>~\frac{d^2x}{d\chi_0^2} \rightarrow \biggl(\frac{1}{\chi_0}\biggr)\frac{d^2\xi}{d\chi_0^2} - \biggl( \frac{2}{\chi_0^2} \biggr) \frac{d\xi}{d\chi_0} + \frac{2\xi}{\chi_0^3} \, .</math>

Doing this, we have,

<math>~0</math>	<math>~=</math>	<math>~ ( 1-\chi_0^2 )\biggl[ \biggl(\frac{1}{\chi_0}\biggr)\frac{d^2\xi}{d\chi_0^2} - \biggl( \frac{2}{\chi_0^2} \biggr) \frac{d\xi}{d\chi_0} + \frac{2\xi}{\chi_0^3} \biggr] + \frac{1}{\chi_0}\biggl[4 - 6\chi_0^2 \biggr] \biggl[ \biggl(\frac{1}{\chi_0}\biggr)\frac{d\xi}{d\chi_0} - \frac{\xi}{\chi_0^2} \biggr] + \mathfrak{F} \biggl( \frac{\xi}{\chi_0} \biggr) </math>
	<math>~=</math>	<math>~\biggl( \frac{1}{\chi_0}\biggr) \biggl\{ ( 1-\chi_0^2 )\biggl[ \frac{d^2\xi}{d\chi_0^2} - \biggl( \frac{2}{\chi_0} \biggr) \frac{d\xi}{d\chi_0} + \frac{2\xi}{\chi_0^2} \biggr] + \biggl[4 - 6\chi_0^2 \biggr] \biggl[ \biggl(\frac{1}{\chi_0}\biggr)\frac{d\xi}{d\chi_0} - \frac{\xi}{\chi_0^2} \biggr] + \mathfrak{F} \xi \biggr\} </math>
	<math>~=</math>	<math>~\biggl( \frac{1}{\chi_0}\biggr) \biggl\{ ( 1-\chi_0^2 )\frac{d^2\xi}{d\chi_0^2} + \frac{1}{\chi_0} \biggl[4 - 6\chi_0^2 \biggr] \frac{d\xi}{d\chi_0} + \mathfrak{F} \xi -\biggl( \frac{2}{\chi_0} \biggr) ( 1-\chi_0^2 )\frac{d\xi}{d\chi_0} + \biggl[4\chi_0^2 -2 \biggr] \frac{\xi}{\chi_0^2} \biggr\} \, , </math>

which, indeed, matches the expression derived via Rosseland's Eulerian formulation.

Rosseland's Derivation of the Wave Equation

Here we step through a derivation of the wave equation as has been presented by S. Rosseland (1969) in chapter 2 of his book titled, The Pulsation Theory of Variable Stars (see, especially his §§ 2.1 & 2.2, pp. 15-20), dropping all terms that account for nonadiabatic effects.

We begin with the set of principal governing equations that provides the foundation for practically all of our discussions in this H_Book, namely, the

Equation of Continuity

<math>\frac{d\rho}{dt} + \rho \nabla \cdot \vec{v} = 0</math>

Euler Equation

<math>\frac{d\vec{v}}{dt} = - \frac{1}{\rho} \nabla P - \nabla \Phi</math>

Adiabatic Form of the
First Law of Thermodynamics

<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math> .

Poisson Equation

<math>\nabla^2 \Phi = 4\pi G \rho</math>

Because we are considering only spherically symmetric configurations, we will implement operators that reflect structural variations only in the radial coordinate. Specifically, following a parallel discussion of the principal governing equations that are appropriate for spherically symmetric configurations, we have the,

Equation of Continuity

<math>\frac{d\rho}{dt} + \rho \biggl[\frac{1}{r^2}\frac{d(r^2 v_r)}{dr} \biggr] = 0 </math>

Euler Equation

Adiabatic Form of the
First Law of Thermodynamics

<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math>

Poisson Equation

<math>\frac{1}{r^2} \biggl[\frac{d }{dr} \biggl( r^2 \frac{d \Phi}{dr} \biggr) \biggr] = 4\pi G \rho </math>

Following Rosseland, we adopt as a supplemental relation what we have referred to elsewhere as,

Form B
of the Ideal Gas Equation of State,

<math>~P = (\gamma_\mathrm{g} - 1)\epsilon \rho </math>

where, for our purposes, we assume that <math>~\gamma_\mathrm{g}</math> is independent of space and time. Plugging the function, <math>~\epsilon(P,\rho)</math>, that is defined by this equation of state into the adiabatic form of the 1^st law of thermodynamics leads to the relations (see, respectively, Rosseland's equations 2.8 and 2.9),

<math>~\frac{\gamma_g P}{\rho} \frac{d\rho}{dt} \, ,</math>

and,

<math>~\biggl( \frac{\rho}{\rho_0}\biggr)^{\gamma_g} \, ,</math>

where <math>~P_0</math> and <math>~\rho_0</math> are independent of time. As was done in our separate, introductory discussion of sound waves, we will assume that we are dealing with an ideal gas and supplement this set of equations with a barotropic (polytropic) equation of state,

<math>~P = K\rho^{\gamma_\mathrm{g}}</math> … with … <math>\gamma_\mathrm{g} \equiv \frac{d\ln P_0}{d\ln \rho_0} = \frac{\rho_0}{P_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \, ,</math>

which will ensure that the adiabatic form of the first law of thermodynamics is satisfied. When we develop the linearized Euler equation, below, it will be useful to recognize that, assuming <math>~\gamma_\mathrm{g}</math> is uniform throughout the fluid, we can rewrite this last expression as,

<math>~\frac{\nabla P_0}{P_0}</math>	<math>~=</math>	<math>~\biggl[\frac{\rho_0}{P_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \frac{\nabla \rho_0}{\rho_0}</math>
<math>~\Rightarrow ~~~ \nabla P_0</math>	<math>~=</math>	<math>~\biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 \, .</math>

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |

Linearizing the Key Relations

Continuity Equation

Lagrangian Perspective

Eulerian Perspective

<math>~- \rho \nabla\cdot\vec{v}</math>

<math>~\frac{\partial\rho}{\partial t}</math>

<math>~- \rho \nabla\cdot\vec{v} - \vec{v}\cdot \nabla\rho</math>

Spherically Symmetric Initial Configurations & Purely Radial Perturbations

<math>~- \frac{\rho}{r^2} \frac{\partial}{\partial r} \biggl( r^2 v_r \biggr)</math>

<math>~\frac{\partial\rho}{\partial t}</math>

<math>~- \frac{\rho}{r^2} \frac{\partial}{\partial r} \biggl( r^2 v_r \biggr) - v_r \frac{\partial \rho}{\partial r}</math>

In an interval of time, <math>~dt = \partial t</math>, a fluid element initially at position <math>~r_0</math> moves to position, <math>~r = r_0 + r_1 = r_0(1 + \xi)</math>. [For later reference, note that <math>~\xi</math> can be a function of <math>~r_0</math> as well as of <math>~t</math>.] On the righthand side of the expression, the radial coordinate will be handled as follows: From the Lagrangian perspective, <math>~r \rightarrow r_0 (1+ \xi)</math>, while from the Eulerian perspective, we want to stay at the original coordinate location, so <math>~r \rightarrow r_0</math>. From both perspectives,

<math>~v_r = \frac{\partial ( r_0 \xi )}{\partial t} = r_0 \frac{\partial \xi}{\partial t} \, .</math>

Riding with the fluid element (Lagrangian perspective), <math>~\rho \rightarrow (\rho_0 + \rho_L) = \rho_0(1+s_L)</math>, while at a fixed coordinate location (Eulerian perspective), <math>~\rho \rightarrow (\rho_0 + \rho_E) = \rho_0(1 + s_E)</math>. Finally, in maintaining a Lagrangian perspective, we will need to ensure that the same element of mass is being tracked as we "ride along" with the fluid element to its new position. For radial perturbations associated with a spherically symmetric configuration, this means that the differential mass in each spherical shell, <math>~dm = 4\pi r^2 \rho dr</math>, must remain constant; that is,

<math>~4\pi r_0^2 \rho_0 dr_0</math>	<math>~=</math>	<math>~4\pi r^2 \rho dr</math>
	<math>~=</math>	<math>~4\pi [r_0(1+\xi)]^2 \rho_0(1+s_L) dr</math>
	<math>~=</math>	<math>~4\pi r_0^2 \rho_0 \biggl(1+2\xi + \cancelto{\scriptstyle\text{small}}{\xi^2} + \cdots \biggr) (1+s_L) dr</math>
	<math>~\approx</math>	<math>~4\pi r_0^2 \rho_0 \biggl(1+2\xi + s_L + 2\cancelto{\scriptstyle\mathrm{small}}{\xi s_L} \biggr) dr</math>
<math>~\Rightarrow~~~ \frac{d}{dr}</math>	<math>~\approx</math>	<math>~(1+2\xi + s_L ) \frac{d}{dr_0} \, .</math>

<math>~\frac{d}{dt}\biggl[\rho_0(1+s_L)\biggr]</math>	<math>~=</math>	<math>~- \biggl\{ \frac{\rho_0(1+\cancelto{}{s_L})}{[r_0(1+\cancelto{}{\xi})]^2} \biggr\}(1+2\cancelto{}{\xi s_L}) \frac{\partial}{\partial r_0} \biggl\{ [r_0(1+\cancelto{}{\xi})]^2 v_r \biggr\}</math>
<math>~\Rightarrow~~~ \frac{d s_L}{dt}</math>	<math>~=</math>	<math>~- \biggl[\frac{2v_r}{r_0} + \frac{\partial v_r}{\partial r_0} \biggr] - \frac{1}{\rho_0} \frac{d\rho_0}{dt}</math>

<math>~\frac{\partial}{\partial t}\biggl[\rho_0(1+s_E)\biggr]</math>	<math>~=</math>	<math>~- \frac{\rho_0(1+\cancelto{\mathrm{small}}{s_E})}{r_0^2} \frac{\partial}{\partial r_0} \biggl( r_0^2 v_r \biggr) - v_r \frac{\partial [\rho_0(1+\cancelto{\mathrm{small}}{s_E})] }{\partial r_0}</math>
<math>~\Rightarrow~~~ \frac{\partial s_E}{\partial t}</math>	<math>~=</math>	<math>~- \biggl[\frac{2v_r}{r_0} + \frac{\partial v_r}{\partial r_0} \biggr] - \frac{v_r}{\rho_0} \frac{\partial \rho_0 }{\partial r_0}</math>

Note: The last term that appears on the righthand side of the two expressions appears to be different. But if, as we are assuming here, <math>~\rho_0</math> has no explicit time dependence but may be considered to be a function of the radial coordinate, <math>~r_0</math>, then the two terms are the same. This is because, quite generically for any scalar function <math>~q</math>, the total time-derivative (Lagrangian perspective) differs from the partial time-derivative (Eulerian perspective) via the expression, <math>dq/dt - \partial q /\partial t = \vec{v}\cdot \nabla q</math>. In our case, <math>~\partial \ln \rho_0/\partial t = 0</math>, so <math>~d\ln\rho_0/dt = \vec{v}\cdot \nabla \ln \rho_0</math>.

<math>~s_L ~~\rightarrow~~ \Delta_L(r_0) e^{i\omega t}</math> … and … <math>~s_E ~~\rightarrow~~ \Delta_E(r_0) e^{i\omega t}</math>

<math>~\xi ~~\rightarrow~~ x(r_0) e^{i\omega t}</math> <math>\Rightarrow</math> <math>~v_r ~~\rightarrow~~ (i\omega)r_0 x(r_0) e^{i\omega t}</math>

<math>~e^{i\omega t} \biggl[ (i\omega)\Delta_L + \frac{d\Delta_L}{dt} \biggr]</math>	<math>~=</math>	<math>~- e^{i\omega t} \biggl[ 2(i\omega)x + (i\omega)x + (i\omega)r_0 \frac{\partial x}{\partial r_0} \biggr]</math>
<math>~\Rightarrow ~~~r_0 \frac{\partial x}{\partial r_0} </math>	<math>~=</math>	<math>~- \Delta_L -3 x - \frac{1}{(i\omega)} \biggl[ v_r \frac{\partial\Delta_L}{\partial r_0} \biggr]</math>
	<math>~=</math>	<math>~- \Delta_L - x \biggl[3 + \cancelto{\scriptstyle\mathrm{small}}{\frac{\partial\Delta_L}{\partial \ln r_0} }\biggr]</math>

<math>~e^{i\omega t} (i\omega)\Delta_E </math>	<math>~=</math>	<math>~- e^{i\omega t} \biggl[ 2(i\omega)x + (i\omega)x + (i\omega)r_0 \frac{\partial x}{\partial r_0} \biggr] - \biggl[\frac{1}{\rho_0} \frac{\partial \rho_0}{\partial r_0} \biggr](i\omega)r_0 x e^{i\omega t}</math>
<math>~\Rightarrow ~~~r_0 \frac{\partial x}{\partial r_0} </math>	<math>~=</math>	<math>~- \Delta_E - x \biggl[3 + \frac{\partial \ln\rho_0}{\partial \ln r_0} \biggr] </math>

User:Tohline/SSC/Perspective Reconciliation

Contents