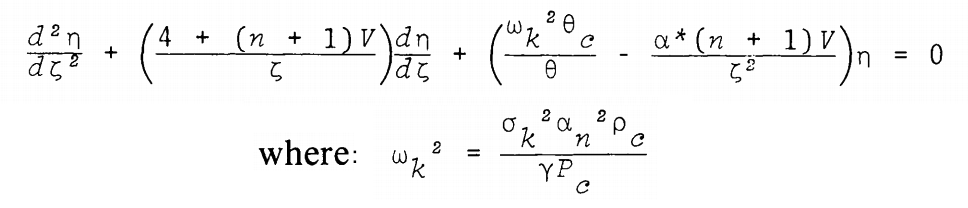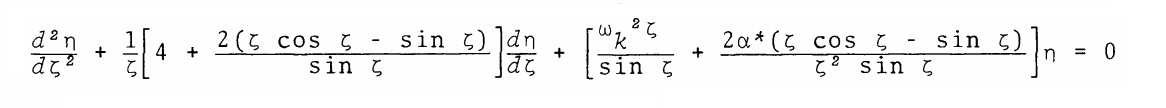User:Tohline/SSC/Stability/Polytropes
Radial Oscillations of Polytropic Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Groundwork
In an accompanying discussion, we derived the so-called,
Adiabatic Wave Equation
<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 \, , </math>
whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. If the initial, unperturbed equilibrium configuration is a polytropic sphere whose internal structure is defined by the function, <math>~\theta(\xi)</math>, then
|
<math>~r_0</math> |
<math>~=</math> |
<math>~a_n \xi \, ,</math> |
|
<math>~\rho_0</math> |
<math>~=</math> |
<math>~\rho_c \theta^{n} \, ,</math> |
|
<math>~P_0</math> |
<math>~=</math> |
<math>~K\rho_0^{(n+1)/n} = K\rho_c^{(n+1)/n} \theta^{n+1} \, ,</math> |
|
<math>~g_0</math> |
<math>~=</math> |
<math>~\frac{GM(r_0)}{r_0^2} = \frac{G}{r_0^2} \biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math> |
where,
|
<math>~a_n</math> |
<math>~=</math> |
<math>~\biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \, .</math> |
Hence, after multiplying through by <math>~a_n^2</math>, the above adiabatic wave equation can be rewritten in the form,
|
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{g_0}{a_n}\biggl(\frac{a_n^2 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\xi} + \biggl(\frac{a_n^2\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{a_n\xi} \biggr] x </math> |
<math>~=</math> |
<math>~0 \, .</math> |
In addition, given that,
|
<math>~\frac{g_0}{a_n}</math> |
<math>~=</math> |
<math>~4\pi G \rho_c \biggl(-\frac{d \theta}{d\xi} \biggr) \, ,</math> |
and,
|
<math>~\frac{a_n^2 \rho_0}{P_0}</math> |
<math>~=</math> |
<math>~\frac{(n+1)}{(4\pi G\rho_c)\theta} = \frac{a_n^2 \rho_c}{P_c} \cdot \frac{\theta_c}{\theta}\, ,</math> |
we can write,
|
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math> |
<math>~=</math> |
<math>0 \, ,</math> |
where we have adopted the functional notation,
|
<math>~V(\xi)</math> |
<math>~\equiv</math> |
<math>~- \frac{\xi}{\theta} \frac{d \theta}{d\xi} \, .</math> |
As can be seen in the following framed image, this is the form of the polytropic wave equation published by J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222), at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models." (It should be noted that there is a sign error in the numerator of the second term of their published expression; the definition of the coefficient, <math>~\alpha^*</math>, given in the text of their paper also contains an error.)
|
Polytropic Wave Equation as Presented by J. O. Murphy & R. Fiedler (1985b) |
|---|
Overview
The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications:
- P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) —
- R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353) — Pulsation Theory
- M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535) — The Oscillations of Gas Spheres
- J. P. Cox (1974, Reports on Progress in Physics, 37, 563) — Pulsating Stars
Tables
|
Quantitative Information Regarding Eigenvectors of Oscillating Polytropes <math>~(\Gamma_1 = 5/3)</math> |
||||
|---|---|---|---|---|
|
<math>~n</math> |
<math>~\frac{\rho_c}{\bar\rho}</math> |
Excerpts from Table 1 of Hurley, Roberts, & Wright (1966) <math>~s^2 (n+1)/(4\pi G\rho_c)</math> |
Excerpts from Table 3 of <math>~\sigma_0^2 R^3/(GM)</math> |
<math>\frac{(n+1) *\mathrm{Cox74}}{3 *\mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math> |
|
<math>~0</math> |
<math>~1</math> |
<math>~1/3</math> |
<math>~1</math> |
<math>~1</math> |
|
<math>~1</math> |
<math>~3.30</math> |
<math>~0.38331</math> |
<math>~1.892</math> |
<math>~0.997</math> |
|
<math>~1.5</math> |
<math>~5.99</math> |
<math>~0.37640</math> |
<math>~2.712</math> |
<math>~1.002</math> |
|
<math>~2</math> |
<math>~11.4</math> |
<math>~0.35087</math> |
<math>~4.00</math> |
<math>~1.000</math> |
|
<math>~3</math> |
<math>~54.2</math> |
<math>~0.22774</math> |
<math>~9.261</math> |
<math>~1.000</math> |
|
<math>~3.5</math> |
<math>~153</math> |
<math>~0.12404</math> |
<math>~12.69</math> |
<math>~1.003</math> |
|
<math>~4.0</math> |
<math>~632</math> |
<math>~0.04056</math> |
<math>~15.38</math> |
<math>~1.000</math> |
n = 1 Polytrope
Setup
From our derived structure of an n = 1 polytrope, in terms of the configuration's radius <math>R</math> and mass <math>M</math>, the central pressure and density are, respectively,
<math>P_c = \frac{\pi G}{8}\biggl( \frac{M^2}{R^4} \biggr) </math> ,
and
<math>\rho_c = \frac{\pi M}{4 R^3} </math> .
Hence the characteristic time and acceleration are, respectively,
<math>
\tau_\mathrm{SSC} = \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} =
\biggl[ \frac{2R^3 }{GM} \biggr]^{1/2} =
\biggl[ \frac{\pi}{2 G\rho_c} \biggr]^{1/2},
</math>
and,
<math>
g_\mathrm{SSC} = \frac{P_c}{R \rho_c} = \biggl( \frac{GM}{2R^2} \biggr) .
</math>
The required functions are,
- Density:
<math>\frac{\rho_0(\chi_0)}{\rho_c} = \frac{\sin(\pi\chi_0)}{\pi\chi_0} </math> ;
- Pressure:
<math>\frac{P_0(\chi_0)}{P_c} = \biggl[ \frac{\sin(\pi\chi_0)}{\pi\chi_0} \biggr]^2 </math> ;
- Gravitational acceleration:
<math>
\frac{g_0(r_0)}{g_\mathrm{SSC}} = \frac{2}{\chi_0^2} \biggl[ \frac{M_r(\chi_0)}{M}\biggr] =
\frac{2}{\pi \chi_0^2} \biggl[ \sin (\pi\chi_0 ) - \pi\chi_0 \cos (\pi\chi_0 ) \biggr].
</math>
So our desired Eigenvalues and Eigenvectors will be solutions to the following ODE:
<math>
\frac{d^2x}{d\chi_0^2} + \frac{2}{\chi_0} \biggl[ 1 + \pi\chi_0 \cot (\pi\chi_0 ) \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl\{ \frac{\pi \chi_0}{\sin(\pi\chi_0)} \biggl[ \frac{\pi \omega^2}{2G\rho_c} \biggr] + \frac{2}{\chi_0^2 } (4 - 3\gamma_\mathrm{g}) \biggl[ 1 - \pi\chi_0 \cot (\pi\chi_0 ) \biggr] \biggr\} x = 0 ,
</math>
or, replacing <math>\chi_0</math> with <math>\xi \equiv \pi\chi_0</math> and dividing the entire expression by <math>\pi^2</math>, we have,
<math>
\frac{d^2x}{d\xi^2} + \frac{2}{\xi} \biggl[ 1 + \xi \cot \xi \biggr] \frac{dx}{d\xi} + \frac{1}{\gamma_\mathrm{g}} \biggl\{ \frac{\xi}{\sin \xi} \biggl[ \frac{\omega^2}{2\pi G\rho_c} \biggr] + \frac{2}{\xi^2 } (4 - 3\gamma_\mathrm{g}) \biggl[ 1 - \xi \cot \xi \biggr] \biggr\} x = 0 .
</math>
This is identical to the formulation of the wave equation that is relevant to the (n = 1) core of the composite polytrope studied by J. O. Murphy & R. Fiedler (1985b); for comparison, their expression is displayed, here, in the following boxed-in image.
|
n = 1 Polytropic Formulation of Wave Equation as Presented by Murphy & Fiedler (1985b) |
|---|
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Attempt at Deriving an Analytic Eigenvector Solution
Multiplying the last expression through by <math>~\xi^2\sin\xi</math> gives,
<math>
(\xi^2\sin\xi ) \frac{d^2x}{d\xi^2} + 2 \biggl[ \xi \sin\xi + \xi^2 \cos \xi \biggr] \frac{dx}{d\xi} +
\biggl[ \sigma^2 \xi^3 - 2\alpha ( \sin\xi - \xi \cos \xi ) \biggr] x = 0 \, ,
</math>
where,
|
<math>~\sigma^2</math> |
<math>~\equiv</math> |
<math> ~\frac{\omega^2}{2\pi G\rho_c \gamma_g} \, , </math> |
|
<math>~\alpha</math> |
<math>~\equiv</math> |
<math> ~3-\frac{4}{\gamma_g} \, . </math> |
The first two terms can be folded together to give,
|
<math>~ \frac{1}{\xi^2 \sin^2\xi} \cdot \frac{d}{d\xi}\biggl[ \xi^2 \sin^2\xi \frac{dx}{d\xi} \biggr] </math> |
<math>~=</math> |
<math> ~\frac{1}{\xi^2 \sin\xi} \biggl[ 2\alpha ( \sin\xi - \xi \cos \xi ) - \sigma^2 \xi^3 \biggr] x </math> |
|
|
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi^2} \biggl( \frac{\xi \cos \xi}{\sin\xi} -1\biggr) + \sigma^2 \biggl( \frac{\xi}{\sin\xi}\biggr) \biggr] x </math> |
|
|
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi^2} \frac{\xi^2}{\sin\xi} \cdot \frac{d}{d\xi} \biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggl( \frac{\xi}{\sin\xi}\biggr) \biggr] x </math> |
|
|
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x \, , </math> |
where, in order to make this next-to-last step, we have recognized that,
|
<math>~ \frac{d}{d\xi} \biggl( \frac{\sin\xi}{\xi} \biggr) </math> |
<math>~=</math> |
<math> ~\frac{\sin\xi}{\xi^2} \biggl[ \frac{\xi \cos\xi}{\sin\xi} - 1 \biggr] \, . </math> |
It would seem that the eigenfunction, <math>~x(\xi)</math>, should be expressible in terms of trigonometric functions and powers of <math>~\xi</math>; indeed, it appears as though the expression governing this eigenfunction would simplify considerably if <math>~x \propto \sin\xi/\xi</math>. With this in mind, we have made some attempts to guess the exact form of the eigenfunction. Here is one such attempt.
First Guess
Let's try,
<math>~x = \frac{\sin\xi}{\xi} \, ,</math>
which means,
|
<math>~x^' \equiv \frac{dx}{d\xi}</math> |
<math>~=</math> |
<math> ~\frac{\sin\xi}{\xi^2} \biggl[ \frac{\xi \cos\xi}{\sin\xi} - 1 \biggr] \, . </math> |
Does this satisfy the governing expression? Let's see. The right-and-side (RHS) gives:
|
RHS |
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x = - \biggl[ \frac{2\alpha x^'}{\xi} + \sigma^2 \biggr] \, . </math> |
At the same time, the left-hand-side (LHS) may, quite generically, be written as:
|
LHS |
<math>~=</math> |
<math>~ \frac{x^'}{\xi} \biggl\{ \frac{\xi}{(\xi^2 \sin^2\xi)x^'} \cdot \frac{d[ (\xi^2 \sin^2\xi)x^']}{d\xi} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{x^'}{\xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] \, . </math> |
Putting the two sides together therefore gives,
|
<math>~ \frac{x^'}{\xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} +2\alpha \biggr] </math> |
<math>~=</math> |
<math> ~-\sigma^2 </math> |
|
<math>~ \Rightarrow ~~~~~ \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']^{1/(2\alpha)}}{d\ln\xi} +1 \biggr] </math> |
<math>~=</math> |
<math> ~- \frac{\sigma^2}{2\alpha } \biggl( \frac{\xi}{x^'} \biggr) </math> |
|
<math>~ \Rightarrow ~~~~~ \frac{d\ln[ (\xi^2 \sin^2\xi)x^']^{-1/(2\alpha)}}{d\ln\xi} </math> |
<math>~=</math> |
<math> ~1 + \frac{\sigma^2}{2\alpha } \biggl( \frac{\xi}{x^'} \biggr) \, . </math> |
[Comment from J. E. Tohline on 6 April 2015: I'm not sure what else to make of this.]
Second Guess
Adopting the generic rewriting of the LHS, and leaving the RHS fully generic as well, we have,
|
<math>~ \frac{x^'}{\xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] </math> |
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x </math> |
|
<math>~\Rightarrow ~~~~~ \frac{x^'}{x} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] </math> |
<math>~=</math> |
<math> ~- 2\alpha\biggl( \frac{\xi}{\sin\xi}\biggr) \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) ~- \sigma^2\biggl( \frac{\xi^2}{\sin\xi}\biggr) </math> |
|
<math>~\Rightarrow ~~~~~ \frac{d\ln(x)}{d\ln \xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] </math> |
<math>~=</math> |
<math> ~- 2\alpha\biggl[ \frac{d\ln(\sin\xi/\xi)}{d\ln \xi} \biggr] ~- \sigma^2\biggl( \frac{\xi^3}{\sin\xi}\biggr) \, . </math> |
|
<math> ~\Rightarrow ~~~~ - \sigma^2 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\sin\xi}{\xi^3}\biggr) \biggl\{\frac{d\ln(x)}{d\ln \xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] + 2\alpha\biggl[ \frac{d\ln(\sin\xi/\xi)}{d\ln \xi} \biggr] \biggr\} \, . </math> |
[Comment from J. E. Tohline on 6 April 2015: I'm not sure what else to make of this.]
Third Guess
Let's rewrite the polytropic (n = 1) wave equation as follows:
<math> ~\sin\xi \biggl[ \xi^2 x^{} + 2\xi x^' - 2\alpha x \biggr] + \cos\xi \biggl[ 2\xi^2 x^' + 2\alpha \xi x \biggr] +\sigma^2 \xi^3 x = 0 \, . </math>
It is difficult to determine what term in the adiabatic wave equation will cancel the term involving <math>~\sigma^2</math> because its leading coefficient is <math>~\xi^3</math> and no other term contains a power of <math>~\xi</math> that is higher than two. After thinking through various trial eigenvector expressions, <math>~x(\xi)</math>, I have determined that a function of the following form has a chance of working because the second derivative of the function generates a leading factor of <math>~\xi^3</math> while the function itself does not introduce any additional factors of <math>~\xi</math> into the term that contains <math>~\sigma^2</math>:
|
<math>~x</math> |
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] [ A\sin\xi + B\cos\xi] </math> |
|
<math>~\Rightarrow ~~~ x^'</math> |
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ \frac{d[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})]}{d\xi} \cdot [ A\sin\xi + B\cos\xi] </math> |
|
|
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{5a \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + b\biggl[ \frac{5}{2} \xi^{3/2}\cos^2(\xi^{5/2}) - \frac{5}{2} \xi^{3/2}\sin^2(\xi^{5/2}) \biggr] - 5c \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) \biggr\} </math> |
|
|
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{5(a-c) \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + \frac{5b}{2} \xi^{3/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ x^{}</math> |
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d^2[ A\sin\xi + B\cos\xi]}{d^2\xi} </math> |
|
|
|
<math>~+ \biggl\{5(a-c) \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + \frac{5b}{2} \xi^{3/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] \biggr\} \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{ \frac{15}{2}(a-c) \xi^{1/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) +\frac{25}{2}(a-c) \xi^{3} \cos^2(\xi^{5/2}) - \frac{25}{2}(a-c) \xi^{3} \sin^2(\xi^{5/2}) </math> |
|
|
|
<math> + \frac{15b}{4} \xi^{1/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] - 25b \xi^{3}\sin(\xi^{5/2}) \cos(\xi^{5/2}) \biggr\} </math> |
|
|
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d^2[ A\sin\xi + B\cos\xi]}{d^2\xi} </math> |
|
|
|
<math>~+ \biggl\{5(a-c) \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + \frac{5b}{2} \xi^{3/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] \biggr\} \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{ \frac{15}{4}\xi^{1/2} \biggl[ 2(a-c) \sin(\xi^{5/2}) \cos(\xi^{5/2}) + b\biggl( 1 - 2\sin^2(\xi^{5/2}) \biggr) \biggr] </math> |
|
|
|
<math>~+ \frac{25}{2} \xi^3 \biggl[ - 2b \sin(\xi^{5/2}) \cos(\xi^{5/2}) +(a-c) \biggl( 1- 2\sin^2(\xi^{5/2}) \biggr) \biggr] \biggr\} </math> |
[Comment from J. E. Tohline on 9 April 2015: I'm not sure what else to make of this.]
Fourth Guess
Again, working with the polytropic (n = 1) wave equation written in the following form,
<math> ~\sin\xi \biggl[ \xi^2 x^{} + 2\xi x^' - 2\alpha x \biggr] + \cos\xi \biggl[ 2\xi^2 x^' + 2\alpha \xi x \biggr] +\sigma^2 \xi^3 x = 0 \, . </math>
Now, let's try:
<math>~x = a_0 + b_1 \xi \sin\xi + c_2 \xi^2 \cos\xi \, ,</math>
which means,
|
<math>~x^' </math> |
<math>~=</math> |
<math> ~b_1 \sin\xi + b_1 \xi \cos\xi + 2c_2 \xi \cos\xi - c_2\xi^2 \sin\xi </math> |
|
|
<math>~=</math> |
<math> ~(b_1 - c_2\xi^2 ) \sin\xi + (b_1 + 2c_2)\xi \cos\xi \, , </math> |
|
<math>~x^{} </math> |
<math>~=</math> |
<math> ~(- 2c_2\xi ) \sin\xi + (b_1 - c_2\xi^2 ) \cos\xi + (b_1 + 2c_2 )\cos\xi - (b_1 + 2c_2 )\xi \sin\xi </math> |
|
|
<math>~=</math> |
<math> ~-(2c_2+b_1 + 2c_2 ) \xi \sin\xi + (2b_1 + 2c_2 - c_2\xi^2 ) \cos\xi \, . </math> |
The LHS of the wave equation then becomes,
|
LHS |
<math>~=</math> |
<math> ~\sin\xi \biggl\{ \xi^2 \biggl[ -(2c_2+b_1 + 2c_2 ) \xi \sin\xi + (2b_1 + 2c_2 - c_2\xi^2 ) \cos\xi \biggr] + 2\xi \biggl[ (b_1 - c_2\xi^2 ) \sin\xi + (b_1 + 2c_2)\xi \cos\xi \biggr] - 2\alpha \biggl[ a_0 + (b_1 \xi) \sin\xi + (c_2 \xi^2) \cos\xi \biggr] \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ 2\xi^2 \biggl[ (b_1 - c_2\xi^2 ) \sin\xi + (b_1 + 2c_2)\xi \cos\xi \biggr] + 2\alpha \xi \biggl[ a_0 + (b_1 \xi) \sin\xi + (c_2 \xi^2) \cos\xi \biggr] \biggr\} +\sigma^2 \xi^3 \biggl[ a_0 + b_1 \xi \sin\xi + c_2 \xi^2 \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\sin\xi \biggl\{ \biggl[ -(2c_2+b_1 + 2c_2 ) \xi^3 \sin\xi + (2b_1 + 2c_2 - c_2\xi^2 ) \xi^2\cos\xi \biggr] + \biggl[ 2(b_1 - c_2\xi^2 )\xi \sin\xi + 2(b_1 + 2c_2)\xi^2 \cos\xi \biggr] - 2\alpha \biggl[ a_0 + (b_1 \xi) \sin\xi + (c_2 \xi^2) \cos\xi \biggr] \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ \biggl[ 2(b_1 - c_2\xi^2 )\xi^2 \sin\xi + 2(b_1 + 2c_2)\xi^3 \cos\xi \biggr] + \biggl[ 2a_0\alpha \xi + 2b_1\alpha \xi^2 \sin\xi + 2c_2 \alpha \xi^3 \cos\xi \biggr] \biggr\} +\sigma^2 \biggl[ a_0\xi^3 + b_1 \xi^4 \sin\xi + c_2 \xi^5 \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\sin\xi \biggl\{- 2\alpha a_0 + \biggl[ -(2c_2+b_1 + 2c_2 ) \xi^3 + 2(b_1 - c_2\xi^2 )\xi - 2\alpha (b_1 \xi) \biggr]\sin\xi + \biggl[ (2b_1 + 2c_2 - c_2\xi^2 ) \xi^2 + 2(b_1 + 2c_2)\xi^2 - 2\alpha (c_2 \xi^2) \biggr] \cos\xi \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ + 2a_0\alpha \xi + \biggl[ 2(b_1 - c_2\xi^2 )\xi^2 + 2b_1\alpha \xi^2 \biggr] \sin\xi + \biggl[ 2(b_1 + 2c_2)\xi^3 + 2c_2 \alpha \xi^3\biggr] \cos\xi \biggr\} +\sigma^2 \biggl[ a_0\xi^3 + b_1 \xi^4 \sin\xi + c_2 \xi^5 \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\sigma^2 a_0 \xi^3 + \biggl[ -(2c_2+b_1 + 2c_2 ) \xi^3 + 2(b_1 - c_2\xi^2 )\xi - 2\alpha (b_1 \xi) \biggr]\sin^2\xi + \biggl[ 2(b_1 + 2c_2)\xi^3 + 2c_2 \alpha \xi^3\biggr] \biggl(1-\sin^2\xi \biggr) </math> |
|
|
|
<math> + \biggl[ (2b_1 + 2c_2 - c_2\xi^2 ) \xi^2 + 2(b_1 + 2c_2)\xi^2 - 2\alpha (c_2 \xi^2) \biggr] \sin\xi \cos\xi + \biggl[ 2(b_1 - c_2\xi^2 )\xi^2 + 2b_1\alpha \xi^2 \biggr] \sin\xi \cos\xi </math> |
|
|
|
<math> +\sigma^2 \biggl[ b_1 \xi^4 \sin\xi + c_2 \xi^5 \cos\xi \biggr] + 2a_0\alpha \xi\cos\xi - 2\alpha a_0 \sin\xi </math> |
|
|
<math>~=</math> |
<math> ~\biggl[ \sigma^2 a_0 + 2(b_1 + 2c_2) + 2c_2 \alpha \biggr]\xi^3 + \biggl\{+ 2(b_1 )\xi - 2\alpha (b_1 \xi) +[-2c_2 - 2(b_1 + 2c_2) - 2c_2 \alpha -(2c_2+b_1 + 2c_2 )] \xi^3 \biggr\} \sin^2\xi </math> |
|
|
|
<math> + \biggl\{ [ (2b_1 + 2c_2 ) + 2(b_1 + 2c_2) - 2\alpha (c_2 ) + 2(b_1 ) + 2b_1\alpha ] \xi^2 -3c_2\xi^4 \biggr\} \sin\xi \cos\xi </math> |
|
|
|
<math>~+ \sin\xi \biggl[\sigma^2b_1 \xi^4 - 2\alpha a_0 \biggr] + \xi \cos\xi \biggl[\sigma^2 c_2 \xi^4 + 2a_0\alpha \biggr] </math> |
|
|
<math>~=</math> |
<math> ~[ \sigma^2 a_0 + 2(b_1 + 2c_2) + 2c_2 \alpha ]\xi^3 + \biggl\{2 b_1(1-\alpha) - [2c_2(5+\alpha) + 3b_1] \xi^2 \biggr\} \xi \sin^2\xi </math> |
|
|
|
<math> + \biggl\{ 2(3-\alpha)( b_1+c_2 ) -3c_2\xi^2 \biggr\} \xi^2 \sin\xi \cos\xi +\sin\xi \biggl[\sigma^2b_1 \xi^4 - 2\alpha a_0 \biggr] + \xi \cos\xi \biggl[\sigma^2 c_2 \xi^4 + 2a_0\alpha \biggr] \, . </math> |
Fifth Guess
Along a similar line of reasoning, let's try a function of the form,
|
<math>~x</math> |
<math>~=</math> |
<math> ~x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\, , </math> |
where <math>~x_s, x_c, x_1, x_2,</math> and <math>~x_3</math> are five separate, as yet, unspecified (polynomial?) functions of <math>~\xi</math>. This also means that,
|
<math>~x^'</math> |
<math>~=</math> |
<math> ~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \, ; </math> |
and,
|
<math>~x^{}</math> |
<math>~=</math> |
<math> ~(x_s^{} - 2x_c^{'} - x_s)\sin\xi + (x_c^{} + 2x_s^' -x_c)\cos\xi + (x_1^{} -2x_3^' -2x_1 + 2x_2)\sin^2\xi + (x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\cos^2\xi + (x_3^{} + 4x_1^' -4x_2^' - 4x_3)\sin\xi \cos\xi \, . </math> |
Hence the LHS of the polytropic (n = 1) wave equation becomes,
|
LHS |
<math>~=</math> |
<math> ~~\sin\xi \biggl\{ \xi^2 \biggl[~(x_s^{} - 2x_c^{'} - x_s)\sin\xi + (x_c^{} + 2x_s^' -x_c)\cos\xi + (x_1^{} -2x_3^' -2x_1 + 2x_2)\sin^2\xi + (x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\cos^2\xi + (x_3^{} + 4x_1^' -4x_2^' - 4x_3)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> + 2\xi \biggl[~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> - 2\alpha \biggl[ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\biggr] \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ 2\xi^2 \biggl[~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> + 2\alpha \xi \biggl[ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\biggr] \biggr\} </math> |
|
|
|
<math> +\sigma^2 \xi^3 \biggl\{ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi \biggr\} </math> |
|
|
<math>~=</math> |
<math> ~~\sin\xi \biggl\{ ~\biggl[(x_s^{} - 2x_c^{'} - x_s)\xi^2 + 2\xi (x_s^' - x_c) -2\alpha x_s \biggr]\sin\xi + \biggl[(x_c^{} + 2x_s^' -x_c)\xi^2 + 2\xi (x_c^' + x_s) - 2\alpha x_c \biggr] \cos\xi </math> |
|
|
|
<math> +\biggl[ (x_1^{} -2x_3^' -2x_1 + 2x_2)\xi^2 + 2\xi (x_1^' - x_3) - 2\alpha x_1 \biggr] \sin^2\xi + \biggl[(x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\xi^2 + 2\xi (x_2^' + x_3) - 2\alpha x_2 \biggr]\cos^2\xi </math> |
|
|
|
<math> + \biggl[(x_3^{} + 4x_1^' -4x_2^' - 4x_3)\xi^2 + 2\xi (x_3^' + 2x_1 -2x_2) - 2\alpha x_3 \biggr] \sin\xi \cos\xi \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ 2\xi^2 \biggl[~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> + 2\alpha \xi \biggl[ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\biggr] \biggr\} </math> |
|
|
|
<math> +\sigma^2 \xi^3 \biggl\{ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi \biggr\} </math> |
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |