User:Tohline/SSC/Virial/FormFactors
Structural Form Factors

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
As has been defined in a companion, introductory discussion, three key dimensionless structural form factors are:
|
<math>~\mathfrak{f}_M </math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{\rho(x)}{\rho_0}\biggr] x^2 dx \, ,</math> |
|
<math>~\mathfrak{f}_W</math> |
<math>~\equiv</math> |
<math>~ 3\cdot 5 \int_0^1 \biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x^2 dx \biggr\} \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x dx\, ,</math> |
|
<math>~\mathfrak{f}_A</math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{P(x)}{P_0}\biggr] x^2 dx \, ,</math> |
where, <math>~x \equiv r/R_\mathrm{limit}</math>, and the subscript "0" denotes central values. The principal purpose of this chapter is to carry out the integrations that are required to obtain expressions for these structural form factors, at least in the few cases where they can be determined analytically. These form-factor expressions will then be used to provide expressions for the two constants, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, that appear in the free-energy function and in the virial theorem, and to provide corresponding expressions for the normalized energies, <math>~W_\mathrm{grav}/E_\mathrm{norm}</math> and <math>~S_\mathrm{therm}/E_\mathrm{norm}</math>.
Generic Reality Check
For embedded (pressure-truncated) polytropic configurations, the normalized virial theorem states that,
|
<math>~2 \biggl( \frac{S_\mathrm{therm}}{E_\mathrm{norm}} \biggr) + \frac{W_\mathrm{grav}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{4\pi P_e R_\mathrm{eq}^3}{E_\mathrm{norm}} \, .</math> |
This provides one mechanism by which the correctness of our form-factor expressions can be checked. Specifically, having determined <math>~S_\mathrm{therm}</math> and <math>~W_\mathrm{grav}</math> from the derived form factors, we can see whether the sum of these energies as specified on the lefthand-side of this virial theorem expression indeed match the normalized energy term involving the external pressure, as specified on the righthand side. In order to facilitate this "reality check" at the end of each example, below, we will use Stahler's detailed force-balanced solution of the equilibrium structure of embedded polytropes to provide an expression for the term on the righthand side of the virial theorem expression.
We begin by plugging our general expression for <math>~E_\mathrm{norm}</math> into this righthand-side term and grouping factors to facilitate insertion of Stahler's expressions.
|
<math>~\frac{4\pi P_e R_\mathrm{eq}^3}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~4\pi P_e R_\mathrm{eq}^3 \biggl[ K^{-n} G^3 M_\mathrm{tot}^{(5-n)} \biggr]^{1/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~4\pi \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{(n-5)/(n-3)} P_e R_\mathrm{eq}^3 \biggl[ K^{-n} G^3 M_\mathrm{limit}^{(5-n)} \biggr]^{1/(n-3)} \, . </math> |
From Stahler's equilibrium solution, we have,
|
<math> ~R_\mathrm{eq} </math> |
<math>~=~</math> |
<math> R_\mathrm{SWS} \biggl( \frac{n}{4\pi} \biggr)^{1/2} \biggl\{ \xi \theta_n^{(n-1)/2} \biggr\}_{\tilde\xi} </math> |
|
|
<math>~=~</math> |
<math>\biggl[ \xi \theta_n^{(n-1)/2} \biggr]_{\tilde\xi} \biggl( \frac{n+1}{4\pi} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} </math> |
|
<math>~\Rightarrow~~~~ ~P_e R_\mathrm{eq}^3 </math> |
<math>~=~</math> |
<math>\biggl[ \xi \theta_n^{(n-1)/2} \biggr]^3_{\tilde\xi} \biggl( \frac{n+1}{4\pi} \biggr)^{3/2} G^{-3/2} K_n^{3n/(n+1)} P_\mathrm{e}^{1 + 3(1-n)/[2(n+1)]} </math> |
|
|
<math>~=~</math> |
<math>\biggl[ \xi \theta_n^{(n-1)/2} \biggr]^3_{\tilde\xi} \biggl( \frac{n+1}{4\pi} \biggr)^{3/2} G^{-3/2} K_n^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, ; </math> |
|
<math> ~M_\mathrm{limit} </math> |
<math>~=~</math> |
<math> M_\mathrm{SWS} \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \biggl\{ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr\}_{\tilde\xi} </math> |
|
|
<math>~=~</math> |
<math>\biggl[ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr]_{\tilde\xi} \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{1/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} </math> |
|
<math>~\Rightarrow~~~~ ~K^{-n} G^3 M_\mathrm{limit}^{(5-n)} </math> |
<math>~=~</math> |
<math>\biggl[ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr]^{(5-n)}_{\tilde\xi} \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{{(5-n)}/2} G^{3-3(5-n)/2} K_n^{-n +2n(5-n)/(n+1)} P_\mathrm{e}^{(3-n)(5-n)/[2(n+1)]} </math> |
|
|
<math>~=~</math> |
<math>\biggl[ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr]^{(5-n)}_{\tilde\xi} \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{{(5-n)}/2} G^{3(n-3)/2} K_n^{3n(3-n)/(n+1)} P_\mathrm{e}^{(3-n)(5-n)/[2(n+1)]} \, ; </math> |
|
<math>~\Rightarrow~~~~ ~P_e R_\mathrm{eq}^3 \biggl[ K^{-n} G^3 M_\mathrm{limit}^{(5-n)} \biggr]^{1/(n-3)} </math> |
<math>~=~</math> |
<math>\biggl\{ \biggl[ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr]_{\tilde\xi} \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{1/2} \biggr\}^{(5-n)/(n-3)} G^{3/2} K_n^{-3n/(n+1)} P_\mathrm{e}^{(n-5)/[2(n+1)]} </math> |
|
|
|
<math>\times ~\biggl[ \xi \theta_n^{(n-1)/2} \biggr]^3_{\tilde\xi} \biggl( \frac{n+1}{4\pi} \biggr)^{3/2} G^{-3/2} K_n^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} </math> |
|
|
<math>~=~</math> |
<math>\biggl\{ \biggl[ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr]^{(5-n)}_{\tilde\xi} \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{(5-n)/2} \biggl[ \xi \theta_n^{(n-1)/2} \biggr]^{3(n-3)}_{\tilde\xi} \biggl( \frac{n+1}{4\pi} \biggr)^{3(n-3)/2} \biggr\}^{1/(n-3)} </math> |
|
|
<math>~=~</math> |
<math>\biggl\{ (n+1)^{3[(5-n)+(n-3)]/2} (4\pi)^{[(n-5)+(9-3n)]/2} \biggl| \frac{d\theta_n}{d\xi} \biggr|^{(5-n)}_{\tilde\xi} (\theta_n)_{\tilde\xi}^{[(n-3)(5-n) + 3(n-1)(n-3)]/2} \tilde\xi^{[2(5-n) + 3(n-3)]} \biggr\}^{1/(n-3)} </math> |
|
|
<math>~=~</math> |
<math> \biggl\{ (n+1)^{3} (4\pi)^{(2-n)} \biggl| \frac{d\theta_n}{d\xi} \biggr|^{(5-n)}_{\tilde\xi} (\theta_n)_{\tilde\xi}^{(n+1)(n-3)} \tilde\xi^{(n+1)} \biggr\}^{1/(n-3)} \, . </math> |
Hence, the expectation based on Stahler's equilibrium models is that,
|
<math>~\frac{4\pi P_e R_\mathrm{eq}^3}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{1/(n-3)} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)\frac{1}{(-\theta'_n)_{\tilde\xi}}\biggr]^{(n-5)/(n-3)} (\theta_n)_{\tilde\xi}^{(n+1)} \tilde\xi^{(n+1)/(n-3)} \, . </math> |
As a cross-check, multiplying this expression through by <math>~[(R_\mathrm{eq}/R_\mathrm{norm})(M_\mathrm{norm}/M_\mathrm{limit})^2]</math> — where the expression for <math>~R_\mathrm{eq}/R_\mathrm{norm}</math> can be obtained from our discussions of detailed force-balanced models — gives a related result that can be obtained directly from Horedt's expressions, namely,
|
<math>~\biggl[ \frac{4\pi P_e R_\mathrm{eq}^4}{G M_\mathrm{limit}^2} \biggr]_\mathrm{Horedt} </math> |
<math>~=</math> |
<math> \frac{\tilde\theta^{n+1} }{(n+1)( -\tilde\theta' )^{2}} \, . </math> |
Viala and Horedt (1974) Expressions
Viala & Horedt (1974) have provided analytic expressions for the gravitational potential energy and the internal energy — which they tag with the variable names, <math>~\Omega</math> and <math>~U</math>, respectively — that we can adopt in our effort to quantify the key structural form factors in the context of pressure-truncated polytropic spheres.
Rewriting these two expressions slightly in order to accommodate our parameter notations, we have from Viala & Horedt's work,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \frac{(4\pi)^2}{(5-n)} \cdot G \rho_c^2 a_n^5 \biggl[\xi^3 \theta^{n+1} + 3\xi^3 (\theta^')^2 - 3(-\xi^2 \theta^')\theta \biggr] \, , </math> |
|
<math>~\mathfrak{S}_\mathrm{A}</math> |
<math>~=</math> |
<math>~ - \frac{n(4\pi)^2}{(5-n)} \cdot G \rho_c^2 a_n^5 \biggl[\frac{2}{(n+1)} \cdot \xi^3 \theta^{n+1} + \xi^3 (\theta^')^2 - (-\xi^2 \theta^')\theta \biggr]_0^{\tilde\xi} \, , </math> |
Both of these energies have been given by Viala & Horedt in terms of the polytropic constant and the central density (they use the notation <math>~\rho_0</math> while we will use <math>~\rho_c</math>). In the context of our discussions, we need to replace the central density with <math>~M_\mathrm{tot}</math> so that (see our table of adopted normalization parameters),
|
<math>~E_\mathrm{norm}</math> |
<math>~=</math> |
<math>~ \biggl[ K^n G^{-3}M_\mathrm{tot}^{n-5} \biggr]^{1/(n-3)} </math> |
can be straightforwardly used for normalization. We have used the notation, <math>~M_\mathrm{tot}</math>, to refer to the mass of an isolated, spherically symmetric polytrope, that is,
|
<math>~M_\mathrm{tot}</math> |
<math>~=</math> |
<math>\frac{4\pi}{3}\cdot \bar\rho (a_n \xi_1)^3 = \frac{4\pi}{3} \biggl(\frac{\bar\rho}{\rho_c}\biggr) \rho_c (a_n \xi_1)^3 \, ,</math> |
where,
|
<math>~a_\mathrm{n}</math> |
<math>~=</math> |
<math>\biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)\biggr]^{1/2} = \biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n}\biggr]^{1/2} \, ,</math> |
|
<math>~\frac{\bar\rho}{\rho_c}</math> |
<math>~=</math> |
<math>~- \biggl( \frac{3\theta^'}{\xi} \biggr)_{\xi_1} \, .</math> |
Hence, we have,
|
<math>~\rho_c</math> |
<math>~=</math> |
<math>~\frac{3}{4\pi} \biggl(\frac{\bar\rho}{\rho_c}\biggr)^{-1} (a_n \xi_1)^{-3} M_\mathrm{tot} </math> |
|
|
<math>~=</math> |
<math>~(4\pi)^{-1} \biggl(-\xi^2 \theta^'\biggr)^{-1}_{\xi_1} \biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n}\biggr]^{-3/2} M_\mathrm{tot} </math> |
|
<math>~\Rightarrow ~~~~~ \rho_c^{(3-n)/2n}</math> |
<math>~=</math> |
<math>~(4\pi)^{1/2} \biggl(-\xi^2 \theta^'\biggr)^{-1}_{\xi_1} \biggl[\frac{G}{(n+1)K}\biggr]^{3/2} M_\mathrm{tot} </math> |
First Detailed Example (n = 5)
Here we complete these integrals to derive detailed expressions for the above subset of structural form factors in the case of spherically symmetric configurations that obey an <math>~n=5</math> polytropic equation of state. The hope is that this will illustrate, in a clear and helpful manner, how the task of calculating form factors is to be carried out, in practice; and, in particular, to provide one nontrivial example for which analytic expressions are derivable. This should simplify the task of debugging numerical algorithms that are designed to calculate structural form factors for more general cases that cannot be derived analytically. The limits of integration will be specified in a general enough fashion that the resulting expressions can be applied, not only to the structures of isolated polytropes, but to pressure-truncated polytropes that are embedded in a hot, tenuous external medium and to the cores of bipolytropes.
Foundation
We use the following normalizations, as drawn from our more general introductory discussion:
|
Adopted Normalizations <math>~(n=5; ~\gamma=6/5)</math> | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||
|
Note that the following relations also hold: <math>~E_\mathrm{norm} = P_\mathrm{norm} R_\mathrm{norm}^3 = \frac{G M_\mathrm{tot}^2}{ R_\mathrm{norm}} = \biggl( \frac{3}{4\pi} \biggr) M_\mathrm{tot} c_\mathrm{norm}^2</math> | |||||||||||||||||||
As is detailed in our accompanying discussion of bipolytropes — see also our discussion of the properties of isolated polytropes — in terms of the dimensionless Lane-Emden coordinate, <math>~\xi \equiv r/a_{5}</math>, where,
<math> a_{5} =\biggr[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_0^{-2/5} \, , </math>
the radial profile of various physical variables is as follows:
|
<math>~\frac{r}{[K^{1/2}/(G^{1/2}\rho_0^{2/5})]}</math> |
<math>~=</math> |
<math>~\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi \, ,</math> |
|
<math>~\frac{\rho}{\rho_0}</math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2} \, ,</math> |
|
<math>~\frac{P}{K\rho_0^{6/5}}</math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3} \, ,</math> |
|
<math>~\frac{M_r}{[K^{3/2}/(G^{3/2}\rho_0^{1/5})]}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr] \, .</math> |
Notice that, in these expressions, the central density, <math>~\rho_0</math>, has been used instead of <math>~M_\mathrm{tot}</math> to normalize the relevant physical variables. We can switch from one normalization to the other by realizing that — see, again, our accompanying discussion — in isolated <math>~n=5</math> polytropes, the total mass is given by the expression,
<math>M_\mathrm{tot} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_0^{-1/5} ~~~~\Rightarrow ~~~~ \rho_0^{1/5} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} M_\mathrm{tot}^{-1} \, .</math>
Employing this mapping to switch to our "preferred" adopted normalizations, as defined in the above boxed-in table, the four radial profiles become,
|
<math>~r^\dagger \equiv \frac{r}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\pi}{2\cdot 3^4} \biggr) \biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi = \biggl( \frac{\pi}{2^3\cdot 3^7} \biggr)^{1/2} \xi \, ,</math> |
|
<math>~\rho^\dagger \equiv \frac{\rho}{\rho_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2^3\cdot 3^6}{\pi} \biggr)^{3/2} \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2} \, ,</math> |
|
<math>~P^\dagger \equiv \frac{P}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2\cdot 3^4}{\pi} \biggr)^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3} \, ,</math> |
|
<math>~\frac{M_r}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\pi}{2\cdot 3^4} \biggr)^{1/2} \biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr] = \biggl[\frac{\xi^2}{3}\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-1}\biggr]^{3/2} \, .</math> |
Mass1
While we already know the expression for the <math>~M_r</math> profile, having copied it from our discussion of detailed force-balanced models of isolated polytropes, let's show how that profile can be derived by integrating over the density profile. After employing the norm-subscripted quantities, as defined above, to normalize the radial coordinate and the mass density in our introductory discussion of the virial theorem, we obtained the following integral defining the,
Normalized Mass:
|
<math>~M_r(r^\dagger) </math> |
<math>~=</math> |
<math> M_\mathrm{tot} \int_0^{r^\dagger} 3(r^\dagger)^2 \rho^\dagger dr^\dagger \, . </math> |
Plugging in the profiles for <math>~r^\dagger</math> and <math>~\rho^\dagger</math>, and recognizing that,
<math>~dr^\dagger = \biggl( \frac{\pi}{2^3\cdot 3^7} \biggr)^{1/2} d\xi \, ,</math>
gives, with the help of Mathematica's Online Integrator,
|
<math>~\frac{M_r(\xi)}{M_\mathrm{tot} } </math> |
<math>~=</math> |
<math> 3 \biggl( \frac{\pi}{2^3\cdot 3^7} \biggr)^{3/2} \biggl( \frac{2^3\cdot 3^6}{\pi} \biggr)^{3/2} \int_0^{\xi} \xi^2 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2} d\xi </math> |
|
|
<math>~=</math> |
<math> 3 \biggl( \frac{1}{3} \biggr)^{3/2} \biggl[ \frac{\xi^3}{3}\biggl(1+\frac{\xi^2}{3}\biggr)^{-3/2} \biggr]_0^{\xi} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \frac{\xi^2}{3}\biggl(1+\frac{\xi^2}{3}\biggr)^{-1}\biggr]^{3/2} \, . </math> |
As it should, this expression exactly matches the normalized <math>~M_r</math> profile shown above. Notice that if we decide to truncate an <math>~n=5</math> polytrope at some radius, <math>~\tilde\xi < \xi_1</math> — as in the discussion that follows — the mass of this truncated configuration will be, simply,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot} } = \frac{M_r({\tilde\xi})}{M_\mathrm{tot} } </math> |
<math>~=</math> |
<math> \biggl[ \frac{\tilde\xi^2}{3}\biggl(1+\frac{\tilde\xi^2}{3}\biggr)^{-1}\biggr]^{3/2} \, . </math> |
Mass2
Alternatively, as has been laid out in our accompanying summary of normalized expressions that are relevant to free-energy calculations,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \int_0^{x} 3x^2 \biggl[ \frac{\rho(x)}{\rho_0} \biggr] dx \, ,</math> |
where, <math>~M_\mathrm{limit}</math> is the "total" mass of the polytropic configuration that is truncated at <math>~R_\mathrm{limit}</math>; keep in mind that, here,
<math>M_\mathrm{tot} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_0^{-1/5} \, ,</math>
is the total mass of the isolated <math>~n=5</math> polytrope, that is, a polytrope whose Lane-Emden radius extends all the way to <math>~\xi_1</math>. In our discussions of truncated polytropes, we often will use <math>~\tilde\xi \le \xi_1</math> to specify the truncated radius in terms of the familiar, dimensionless Lane-Emden radial coordinate, so here we will set,
<math>~R_\mathrm{limit} = a_5 \tilde\xi ~~~~\Rightarrow ~~~~ x = \frac{r}{R_\mathrm{limit}} = \frac{a_5 \xi}{a_5 \tilde\xi} = \frac{\xi}{\tilde\xi} \, .</math>
Hence, in terms of the desired integration coordinate, <math>~x</math>, the density profile provided above becomes,
|
and the integral defining <math>~M_r(x)</math> becomes,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \int_0^{x} 3x^2 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} dx </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} \, .</math> |
In this case, integrating "all the way out to the surface" means setting <math>~r = R_\mathrm{limit}</math> and, hence, <math>~x = 1</math>; by definition, it also means <math>~M_r(x) = M_\mathrm{limit}</math>. Therefore we have,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\bar\rho}{\rho_c} \biggr)_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} \, .</math> |
Using this expression for the mean-to-central density ratio along with the expression for the ratio, <math>~M_\mathrm{limit}/M_\mathrm{tot}</math>, derived in the preceding subsection, we also can state that for truncated <math>~n=5</math> polytropes,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{3/2} \biggl[ \frac{\tilde\xi^2}{3}\biggl(1+\frac{\tilde\xi^2}{3}\biggr)^{-1}\biggr]^{3/2} \biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{\tilde\xi^2}{3}\biggr]^{3/2} \biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} \, .</math> |
By making the substitution, <math>~x \rightarrow \xi/\tilde\xi</math>, this expression becomes identical to the <math>~M_r/M_\mathrm{tot}</math> profile presented just before the "Mass1" subsection, above. In summary, then, we have the following two equally valid expressions for the <math>~M_r</math> profile — one expressed as a function of <math>~\xi</math> and the other expressed as a function of <math>~x</math>:
|
Mean-to-Central Density
From the above line of reasoning we appreciate that, for any spherically symmetric configuration, the ratio of the configuration's mean density to its central density can be obtained by setting the upper limit of our just-completed "Mass2" integration to <math>~x=1</math>. That is to say, quite generally,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \int_0^{1} 3x^2 \biggl[ \frac{\rho(x)}{\rho_0} \biggr] dx </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\bar\rho}{\rho_c} \biggr)_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \int_0^{1} 3x^2 \biggl[ \frac{\rho(x)}{\rho_0} \biggr] dx </math> |
But the integral expression on the righthand side of this relation is also the definition of the structural form factor, <math>~\mathfrak{f}_M</math>, given at the top of this page. Hence, we can say, quite generally, that,
<math>~\mathfrak{f}_M = \frac{\bar\rho}{\rho_c} \, .</math>
And, given that we have just completed this integral for the case of truncated <math>~n=5</math> polytropic structures, we can state, specifically, that,
<math>~\mathfrak{f}_M\biggr|_{n=5} = \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} \, .</math>
Gravitational Potential Energy
As presented at the top of this page, the structural form factor associated with determination of the gravitational potential energy is,
|
<math>~\mathfrak{f}_W</math> |
<math>~\equiv</math> |
<math>~ 3\cdot 5 \int_0^1 \biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x^2 dx \biggr\} \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x dx\, .</math> |
Given that an expression for the normalized density profile, <math>~\rho(x)/\rho_0</math>, has already been determined, above, we can carry out the nested pair of integrals immediately. Indeed, the integral contained inside of the curly braces has already been completed in the "Mass2" subsection, above, in order to determine the radial mass profile. Specifically, we have already determined that,
|
<math>~\biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x^2 dx \biggr\} </math> |
<math>~=</math> |
<math>~\frac{1}{3} \biggl\{ \int_0^{x} 3x^2 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} dx\biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{3} \biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} \, .</math> |
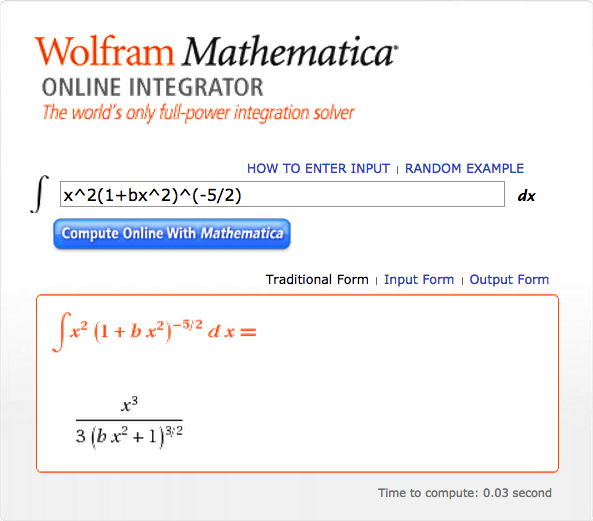
Hence, with the help of Mathematica's Online Integrator, we have,
|
<math>~\mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ 5 \int_0^1 \biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} x dx </math> |
|
|
<math>~=</math> |
<math>~ 5 \int_0^1 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-4} x^4 dx </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2^4\cdot 3} \biggl( \frac{\tilde\xi^2}{3}\biggr)^{-5/2} \biggl(1 + \frac{\tilde\xi^2}{3}\biggr)^{-3} \biggl\{ \biggl( \frac{\tilde\xi^2}{3}\biggr)^{1/2} \biggl[ 3\biggl( \frac{\tilde\xi^2}{3}\biggr)^2 - 8\biggl( \frac{\tilde\xi^2}{3}\biggr) - 3 \biggr] + 3\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr)^3\tan^{-1}\biggl[ \biggl( \frac{\tilde\xi^2}{3}\biggr)^{1/2} \biggr] \biggr\} \, . </math> |
|
ASIDE: Now that we have expressions for, both, <math>~\mathfrak{f}_M</math> and <math>~\mathfrak{f}_W</math>, we can determine an analytic expression for the normalized gravitational potential energy for truncated, <math>~n=5</math> polytropes. As is shown in a companion discussion,
where,
In order to simplify typing, we will switch to the variable, <math>~\ell \equiv \frac{\tilde\xi}{\sqrt{3}} ~~~\Rightarrow~~~~ \frac{\tilde\xi^2}{3} = \ell^2 \, ,</math> in which case a summary of derived expressions, from above, gives,
Hence,
This exactly matches the normalized gravitational potential energy derived independently in the context of our exploration of <math>~(n_c, n_e) = (5,1)</math> bipolytropes, referred to in that discussion as <math>~W_\mathrm{core}^*</math>.
Hence, also, as defined in the accompanying introductory discussion, the constant, <math>\mathcal{A}</math>, that appears in our general free-energy equation is (for <math>~n=5</math> polytropic configurations),
|
Thermal Energy
As presented at the top of this page, the structural form factor associated with determination of the configuration's thermal energy is,
|
<math>~\mathfrak{f}_A</math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{P(x)}{P_0}\biggr] x^2 dx \, ,</math> |
Given that an expression for the normalized pressure profile, <math>~P/P_0</math>, has already been provided, above, we can carry out the integral immediately. Specifically, we have,
|
<math>~\frac{P(\xi)}{P_0} </math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{\xi^2}{3} \biggr)^{-3}</math> |
|
<math>~\Rightarrow ~~~~ \frac{P(x)}{P_0} </math> |
<math>~=</math> |
<math>~\biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x \biggr]^{-3} \, .</math> |
Hence, with the aid of Mathematica's Online Integrator, the relevant integral gives,
|
<math>~\mathfrak{f}_A</math> |
<math>~\equiv</math> |
<math>~ 3\int_0^1 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x \biggr]^{-3} x^2 dx </math> |
|
|
<math>~\equiv</math> |
<math>~ \frac{3}{2^3} \biggl\{\biggl(\frac{\tilde\xi^2}{3}\biggr)^{-3/2} \tan^{-1}\biggl[ \biggl(\frac{\tilde\xi^2}{3}\biggr)^{1/2} \biggr] + \biggl(\frac{\tilde\xi^2}{3}\biggr)^{-1}\biggl[1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)\biggr]^{-1} - 2\biggl(\frac{\tilde\xi^2}{3}\biggr)^{-1}\biggl[1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)\biggr]^{-2} \biggr\} \, . </math> |
|
ASIDE: Having this expression for <math>~\mathfrak{f}_A</math> allows us to determine an analytic expression for the coefficient, <math>~\mathcal{B}</math>, that appears in our general expression for the free energy, and that can be straightforwardly used to obtain an expression for the thermal energy content of <math>~n=5 (\gamma=6/5)</math> polytropic configurations. From our accompanying introductory discussion, we have,
If, as above, we adopt the simplifying variable notation, <math>~\ell \equiv \frac{\tilde\xi}{\sqrt{3}} ~~~\Rightarrow~~~~ \frac{\tilde\xi^2}{3} = \ell^2 \, ,</math> the various factors in the definition of <math>~\mathcal{B}</math> and <math>~S_\mathrm{therm}</math> are (see above),
Hence,
This exactly matches the normalized thermal energy derived independently in the context of our exploration of <math>~(n_c, n_e) = (5,1)</math> bipolytropes, referred to in that discussion as <math>~S_\mathrm{core}^*</math>. Its similarity to the expression for the gravitational potential energy — which is relevant to the virial theorem — is more apparent if it is rewritten in the following form:
|
Summary (n=5)
In summary, for <math>~n=5</math> structures we have,
|
Structural Form Factors (n = 5) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
|
Free-Energy Coefficients (n = 5) | |||||||||
| |||||||||
|
Normalized Energies (n = 5) | |||||||||
|
Reality Check (n=5)
|
<math>~2\biggl(\frac{S_\mathrm{therm}}{E_\mathrm{norm}}\biggr)+ \frac{W_\mathrm{grav}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{3^{8}}{2^{5}\pi}\biggr)^{1/2}\biggl\{ [ \ell (\ell^4-1) (1+\ell^2)^{-3} + \tan^{-1}(\ell )] - \biggl[\ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1+\ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{3^{8}}{2^{5}\pi}\biggr)^{1/2} \biggl[\frac{8}{3}\ell^3 (1+\ell^2)^{-3}\biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{2 \cdot 3^{6}}{\pi}\biggr)^{1/2} \biggl[\frac{\ell}{ (1+\ell^2)} \biggr]^3 \, . </math> |
For embedded polytropes, this should be compared against the expectation (prediction) provided by Stahler's equilibrium models, as detailed above. Given that, for <math>~n=5</math> polytropes — see the "Mass1" discussion above and our accompanying tabular summary of relevant properties,
|
<math> ~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} = \biggl[ \ell^2(1+\ell^2)^{-1} \biggr]^{3/2} </math> |
; |
<math> ~\theta_5 = ( 1 + \ell^2 )^{-1/2} </math> |
and |
<math> ~-\frac{d\theta_5}{d\xi} \biggr|_{\xi_e} = 3^{1/2} \ell ( 1 + \ell^2 )^{-3/2} \, , </math> |
the expectation is that,
|
<math>~\frac{4\pi P_e R_\mathrm{eq}^3}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{1/(n-3)} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)\frac{1}{(-\theta'_n)_{\tilde\xi}}\biggr]^{(n-5)/(n-3)} (\theta_n)_{\tilde\xi}^{(n+1)} \tilde\xi^{(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{2\cdot 3^3}{\pi}\biggr]^{1/2} ( 1 + \ell^2 )^{-3} (3^{1/2}\ell)^{3} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2\cdot 3^6}{\pi}\biggr)^{1/2} \biggl[ \frac{\ell}{( 1 + \ell^2 )} \biggr]^{3} \, . </math> |
This precisely matches our sum of the thermal and gravitational potential energies, as just determined using our expressions for the structural form factors. This gives us confidence that our form-factor expressions are correct, at least in the case of embedded <math>~n=5</math> polytropic structures.
Second Detailed Example (n = 1)
Foundation
We use the following normalizations, as drawn from our more general introductory discussion:
|
Adopted Normalizations <math>~(n=1; ~\gamma=2)</math> | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||
|
Note that the following relations also hold: <math>~E_\mathrm{norm} = P_\mathrm{norm} R_\mathrm{norm}^3 = \frac{G M_\mathrm{tot}^2}{ R_\mathrm{norm}} = \biggl( \frac{3}{4\pi} \biggr) M_\mathrm{tot} c_\mathrm{norm}^2</math> | |||||||||||||||||||
As is detailed in our discussion of the properties of isolated polytropes, in terms of the dimensionless Lane-Emden coordinate, <math>~\xi \equiv r/a_{1}</math>, where,
<math> a_{1} = \biggl( \frac{K}{2\pi G} \biggr)^{1/2} \, , </math>
the radial profile of various physical variables is as follows:
|
<math>~\frac{r}{(K/G)^{1/2}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{1}{2\pi} \biggr)^{1/2} \xi \, ,</math> |
|
<math>~\frac{\rho}{\rho_0}</math> |
<math>~=</math> |
<math>~\frac{\sin\xi}{\xi} \, ,</math> |
|
<math>~\frac{P}{K\rho_0^2}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\sin\xi}{\xi} \biggr)^{2} \, ,</math> |
|
<math>~\frac{M_r}{(K/G)^{3/2}\rho_0}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2}{\pi} \biggr)^{1/2} (\sin\xi - \xi \cos\xi) \, .</math> |
Notice that, in these expressions, the central density, <math>~\rho_0</math>, has been used instead of <math>~M_\mathrm{tot}</math> to normalize the relevant physical variables. We can switch from one normalization to the other by realizing that — see, again, our accompanying discussion — in isolated <math>~n=1</math> polytropes, the total mass is given by the expression,
<math>M_\mathrm{tot} = \biggr[ \frac{2\pi K^3}{G^3} \biggr]^{1/2} \rho_0 ~~~~\Rightarrow ~~~~ \rho_0 = \biggr[ \frac{G^3}{2\pi K^3} \biggr]^{1/2} M_\mathrm{tot} \, .</math>
Employing this mapping to switch to our "preferred" adopted normalizations, as defined in the above boxed-in table, the four radial profiles become,
|
<math>~r^\dagger \equiv \frac{r}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1}{2\pi} \biggr)^{1/2} \xi \, ,</math> |
|
<math>~\rho^\dagger \equiv \frac{\rho}{\rho_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2^3 \pi}{3^2} \biggr)^{1/2} \frac{\sin\xi}{\xi} \, ,</math> |
|
<math>~P^\dagger \equiv \frac{P}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{1}{2\pi} \biggl( \frac{\sin\xi}{\xi}\biggr)^2 \, ,</math> |
|
<math>~\frac{M_r}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi} (\sin\xi - \xi \cos\xi) \, .</math> |
Mass1
While we already know the expression for the <math>~M_r</math> profile, having copied it from our discussion of detailed force-balanced models of isolated polytropes, let's show how that profile can be derived by integrating over the density profile. After employing the norm-subscripted quantities, as defined above, to normalize the radial coordinate and the mass density in our introductory discussion of the virial theorem, we obtained the following integral defining the,
Normalized Mass:
|
<math>~M_r(r^\dagger) </math> |
<math>~=</math> |
<math> M_\mathrm{tot} \int_0^{r^\dagger} 3(r^\dagger)^2 \rho^\dagger dr^\dagger \, . </math> |
Plugging in the profiles for <math>~r^\dagger</math> and <math>~\rho^\dagger</math> gives, with the help of Mathematica's Online Integrator,
|
<math>~\frac{M_r(\xi)}{M_\mathrm{tot} } </math> |
<math>~=</math> |
<math> 3 \int_0^{\xi} \frac{\xi^2}{2\pi} \biggl( \frac{2^3\pi}{3^2} \biggr)^{1/2} \frac{\sin\xi}{\xi} \cdot \frac{d\xi }{(2\pi)^{1/2}} </math> |
|
|
<math>~=</math> |
<math> 3( 2\pi)^{-3/2}\biggl( \frac{2^3\pi}{3^2} \biggr)^{1/2} \int_0^{\xi} \xi \sin\xi d\xi </math> |
|
|
<math>~=</math> |
<math> \frac{1}{\pi} (\sin\xi - \xi\cos\xi) \, . </math> |
As it should, this expression exactly matches the normalized <math>~M_r</math> profile shown above. Notice that if we decide to truncate an <math>~n=1</math> polytrope at some radius, <math>~\tilde\xi < \xi_1</math> — as in the discussion that follows — the mass of this truncated configuration will be, simply,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot} } = \frac{M_r({\tilde\xi})}{M_\mathrm{tot} } </math> |
<math>~=</math> |
<math> \frac{1}{\pi} (\sin\tilde\xi - \tilde\xi \cos\tilde\xi) \, . </math> |
Mass2
Alternatively, as has been laid out in our accompanying summary of normalized expressions that are relevant to free-energy calculations,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \int_0^{x} 3x^2 \biggl[ \frac{\rho(x)}{\rho_0} \biggr] dx \, ,</math> |
where, <math>~M_\mathrm{limit}</math> is the "total" mass of the polytropic configuration that is truncated at <math>~R_\mathrm{limit}</math>; keep in mind that, here,
<math>M_\mathrm{tot} = \biggr[ \frac{2\pi K^3}{G^3} \biggr]^{1/2} \rho_0 \, ,</math>
is the total mass of the isolated <math>~n=1</math> polytrope, that is, a polytrope whose Lane-Emden radius extends all the way to <math>~\xi_1 = \pi</math>. In our discussions of truncated polytropes, we often will use <math>~\tilde\xi \le \xi_1</math> to specify the truncated radius in terms of the familiar, dimensionless Lane-Emden radial coordinate, so here we will set,
<math>~R_\mathrm{limit} = a_1 \tilde\xi ~~~~\Rightarrow ~~~~ x = \frac{r}{R_\mathrm{limit}} = \frac{a_1 \xi}{a_1 \tilde\xi} = \frac{\xi}{\tilde\xi} \, .</math>
Hence, in terms of the desired integration coordinate, <math>~x</math>, the density profile provided above becomes,
|
and the integral defining <math>~M_r(x)</math> becomes,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{3}{\tilde\xi} \int_0^{x} x \sin(\tilde\xi x) dx </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{3}{\tilde\xi^3} [\sin(\tilde\xi x) - (\tilde\xi x)\cos(\tilde\xi x) ] \, . </math> |
In this case, integrating "all the way out to the surface" means setting <math>~r = R_\mathrm{limit}</math> and, hence, <math>~x = 1</math>; by definition, it also means <math>~M_r(x) = M_\mathrm{limit}</math>. Therefore we have,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{3}{\tilde\xi^3} [\sin \tilde\xi - \tilde\xi \cos \tilde\xi ] </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\bar\rho}{\rho_c} \biggr)_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \frac{3}{\tilde\xi^3} [\sin \tilde\xi - \tilde\xi \cos \tilde\xi ] \, .</math> |
Using this expression for the mean-to-central density ratio along with the expression for the ratio, <math>~M_\mathrm{limit}/M_\mathrm{tot}</math>, derived in the preceding subsection, we also can state that for truncated <math>~n=5</math> polytropes,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi} (\sin\tilde\xi - \tilde\xi \cos\tilde\xi) \biggl\{ \frac{[\sin(\tilde\xi x) - (\tilde\xi x)\cos(\tilde\xi x) ]}{( \sin \tilde\xi - \tilde\xi \cos \tilde\xi )} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\pi} [\sin(\tilde\xi x) - (\tilde\xi x)\cos(\tilde\xi x) ] </math> |
By making the substitution, <math>~x \rightarrow \xi/\tilde\xi</math>, this expression becomes identical to the <math>~M_r/M_\mathrm{tot}</math> profile presented just before the "Mass1" subsection, above. In summary, then, we have the following two equally valid expressions for the <math>~M_r</math> profile — one expressed as a function of <math>~\xi</math> and the other expressed as a function of <math>~x</math>:
|
Mean-to-Central Density
Following the line of reasoning provided above, we can use the just-derived central-to-mean density ratio to specify one of the structural form factors. Specifically,
<math>~\mathfrak{f}_M\biggr|_{n=1} = \frac{\bar\rho}{\rho_c} = \frac{3}{\tilde\xi^3} [\sin \tilde\xi - \tilde\xi \cos \tilde\xi ] \, .</math>
Gravitational Potential Energy
As presented at the top of this page, the structural form factor associated with determination of the gravitational potential energy is,
|
<math>~\mathfrak{f}_W</math> |
<math>~\equiv</math> |
<math>~ 3\cdot 5 \int_0^1 \biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x^2 dx \biggr\} \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x dx\, .</math> |
From the derivations already presented, above, for <math>~n=1</math> polytropic configurations, we know all of the functions under this integral. We know, for example, that,
|
<math>~\biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_0}\biggr] x^2 dx \biggr\} </math> |
<math>~=</math> |
<math>~\frac{1}{\tilde\xi^3} [\sin(\tilde\xi x) - (\tilde\xi x)\cos(\tilde\xi x) ] \, .</math> |
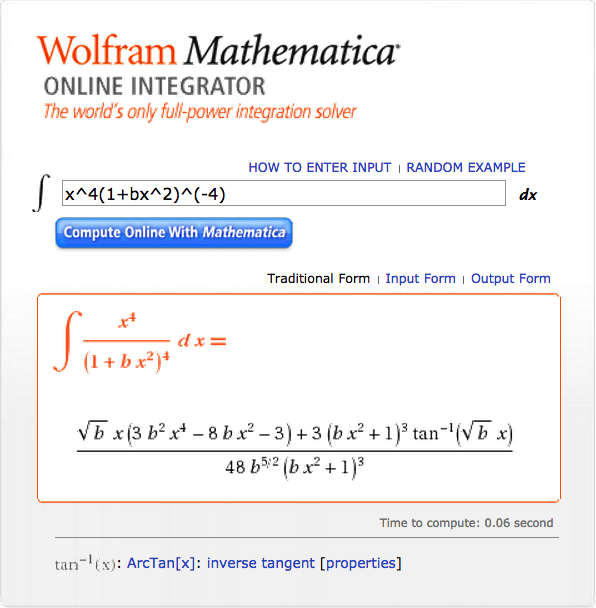
Hence, with the help of Mathematica's Online Integrator, we have,
|
<math>~\mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \frac{3\cdot 5}{\tilde\xi^4} \int_0^1 \biggl\{ [\sin(\tilde\xi x) - (\tilde\xi x)\cos(\tilde\xi x) ] \biggr\} \sin(\tilde\xi x) dx </math> |
|
|
<math>~=</math> |
<math>~ \frac{3\cdot 5}{\tilde\xi^4} \biggl\{ \frac{x}{2} - \frac{\sin(2\tilde\xi x)}{4\tilde\xi} - \tilde\xi\biggl[ \frac{\sin(2\tilde\xi x) - 2\tilde\xi x\cos(2\tilde\xi x)}{8\tilde\xi^2} \biggr] \biggr\}_0^1 </math> |
|
|
<math>~=</math> |
<math>~ \frac{3\cdot 5}{2^3 \tilde\xi^6} \biggl[ 4\tilde\xi^2 - 3\tilde\xi \sin(2\tilde\xi) + 2\tilde\xi^2 \cos(2\tilde\xi ) \biggr] \, . </math> |
|
ASIDE: Now that we have expressions for, both, <math>~\mathfrak{f}_M</math> and <math>~\mathfrak{f}_W</math>, we can determine an analytic expression for the normalized gravitational potential energy for truncated, <math>~n=1</math> polytropes. As is shown in a companion discussion,
where,
A summary of derived expressions, from above, gives,
Hence,
|
Thermal Energy
As presented at the top of this page, the structural form factor associated with determination of the configuration's thermal energy is,
|
<math>~\mathfrak{f}_A</math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{P(x)}{P_0}\biggr] x^2 dx \, ,</math> |
Given that an expression for the normalized pressure profile, <math>~P/P_0</math>, has already been provided, above, we can carry out the integral immediately. Specifically, we have,
|
<math>~\frac{P(\xi)}{P_0} </math> |
<math>~=</math> |
<math>~\biggl( \frac{\sin\xi}{\xi}\biggr)^{2}</math> |
|
<math>~\Rightarrow ~~~~ \frac{P(x)}{P_0} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{\sin(\tilde\xi x)}{(\tilde\xi x)}\biggr]^{2} \, .</math> |
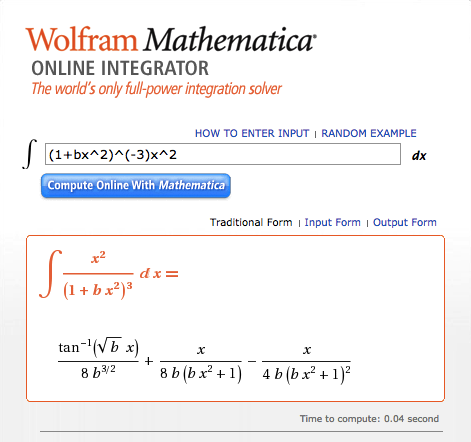
Hence, with the aid of Mathematica's Online Integrator, the relevant integral gives,
|
<math>~\mathfrak{f}_A</math> |
<math>~=</math> |
<math>~ \frac{3}{\tilde\xi^2} \int_0^1 \sin^2(\tilde\xi x) dx </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{\tilde\xi^2} \biggl[\frac{x}{2}- \frac{\sin(2\tilde\xi x)}{4\tilde\xi} \biggr]_0^1 = \frac{3}{2^2\tilde\xi^3} \biggl[2\tilde\xi - \sin(2\tilde\xi ) \biggr] \, . </math> |
|
ASIDE: Having this expression for <math>~\mathfrak{f}_A</math> allows us to determine an analytic expression for the coefficient, <math>~\mathcal{B}</math>, that appears in our general expression for the free energy, and that can be straightforwardly used to obtain an expression for the thermal energy content of <math>~n=1 (\gamma=2)</math> polytropic configurations. From our accompanying introductory discussion, we have,
The various factors in the definition of <math>~\mathcal{B}</math> and <math>~S_\mathrm{therm}</math> are (see above),
Hence,
|
Summary (n=1)
In summary, for <math>~n=1</math> structures we have,
|
Structural Form Factors (n = 1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
|
Free-Energy Coefficients (n = 1) | |||||||||
| |||||||||
|
Normalized Energies (n = 1) | |||||||||
|
Reality Check (n=1)
Expectation from Stahler's Equilibrium Models
|
<math>~2\biggl(\frac{S_\mathrm{therm}}{E_\mathrm{norm}}\biggr)+ \frac{W_\mathrm{grav}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{1}{2^{5}\pi^3} \biggr)^{1/2} \biggl\{ \biggl[6\tilde\xi - 3\sin(2\tilde\xi ) \biggr] - \biggl[ 4\tilde\xi - 3 \sin(2\tilde\xi) + 2\tilde\xi \cos(2\tilde\xi ) \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{1}{2^{5}\pi^3} \biggr)^{1/2} 2\tilde\xi\biggl\{ 1-\cos(2\tilde\xi ) \biggr\} = \biggl( \frac{1}{2\pi^3} \biggr)^{1/2} \tilde\xi \sin^2(\tilde\xi ) \, . </math> |
For embedded polytropes, this should be compared against the expectation (prediction) provided by Stahler's equilibrium models, as detailed above. Given that, for <math>~n=1</math> polytropes — see the "Mass1" discussion above and our accompanying tabular summary of relevant properties,
|
<math> ~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} = \frac{1}{\pi}(\sin\tilde\xi - \tilde\xi \cos\tilde\xi) </math> |
; |
<math> ~\theta_1 = \frac{\sin\tilde\xi}{\tilde\xi} </math> |
and |
<math> ~-\frac{d\theta_1}{d\xi} \biggr|_{\tilde\xi} = \frac{1}{\tilde\xi^2}(\sin\tilde\xi - \tilde\xi \cos\tilde\xi) \, , </math> |
the expectation is that,
|
<math>~\frac{4\pi P_e R_\mathrm{eq}^3}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{1/(n-3)} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)\frac{1}{(-\theta'_n)_{\tilde\xi}}\biggr]^{(n-5)/(n-3)} (\theta_n)_{\tilde\xi}^{(n+1)} \tilde\xi^{(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{2}{\pi} \biggr]^{-1/2} \biggl[ \frac{1}{\pi}(\sin\tilde\xi - \tilde\xi \cos\tilde\xi) \tilde\xi^2(\sin\tilde\xi - \tilde\xi \cos\tilde\xi)^{-1}\biggr]^{2} \biggl( \frac{\sin\tilde\xi}{\tilde\xi}\biggr)^2 \tilde\xi^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{1}{2\pi^3}\biggr)^{1/2} \tilde\xi \sin^2\tilde\xi \, . </math> |
This precisely matches our sum of the thermal and gravitational potential energies, as just determined using our expressions for the structural form factors, giving us additional confidence that our form-factor expressions are correct.
Earlier Assumption About Form-Factor Expressions
In our introductory development of structural form factors, we surmised that,
|
Structural Form Factors for Pressure-Truncated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Specifically in the case of <math>~n=1</math> polytropic structures, therefore, the expectation was that (tilde notation is omitted for simplicity),
|
<math>~\mathfrak{f}_M</math> |
<math>~=</math> |
<math>~ 3\xi^{-3} (\sin\xi - \xi \cos\xi) \, ;</math> |
|
<math>~\mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \biggl( \frac{3^2\cdot 5}{2^2} \biggr) \xi^{-6} (\sin\xi - \xi \cos\xi)^2</math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3\cdot 5}{2^3 \xi^6} \biggr) 6(\sin^2\xi - 2\xi \sin\xi \cos\xi + \xi^2\cos^2\xi) </math> |
|
<math>~\mathfrak{f}_A</math> |
<math>~=</math> |
<math>~ \biggl( \frac{3}{2} \biggr) \xi^{-4} (\sin\xi - \xi \cos\xi)^2 + \frac{\sin^2\xi}{\xi^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\xi^4} \biggl[ 3(\sin\xi - \xi \cos\xi)^2 +2 \xi^2 \sin^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\xi^4} \biggl[ 3(\sin^2\xi - 2\xi\sin\xi \cos\xi +\xi^2 \cos^2\xi) +2 \xi^2 \sin^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\xi^4} \biggl[- 3\xi\sin(2\xi) + 3\sin^2\xi +3\xi^2 (1-\sin^2\xi) +2 \xi^2 \sin^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\xi^4} \biggl[3\xi^2 - 3\xi\sin(2\xi) + 3\sin^2\xi - \xi^2 \sin^2\xi \biggr] </math> |
Fiddling Around
In this subsection, for simplicity, we will omit the "tilde" over the variable <math>~\xi</math>. In the case of <math>~n=1</math> structures,
|
<math>~\theta^{n+1}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\sin\xi}{\xi}\biggr)^2 = \frac{1}{2\xi^2} \biggl[ 1 - \cos(2\xi) \biggr] = \frac{1}{2^2\xi^3} \biggl[ 2\xi - 2\xi\cos(2\xi) \biggr] </math> |
|
<math>~\Rightarrow ~~~\mathfrak{f}_A - \theta^{n+1}</math> |
<math>~=</math> |
<math>~ \frac{1}{2^2\xi^3} \biggl[6\xi - 3\sin(2\xi ) \biggr] - \frac{1}{2^2\xi^3} \biggl[ 2\xi - 2\xi\cos(2\xi) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2^2\xi^3} \biggl[4\xi - 3\sin(2\xi ) + 2\xi\cos(2\xi) \biggr] \, . </math> |
But, we also have shown that,
|
<math>~\biggl( \frac{2^3 \xi^5}{3\cdot 5} \biggr) \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \biggl[ 4\xi - 3\sin(2\xi) + 2\xi \cos(2\xi ) \biggr] \, . </math> |
Hence, we see that,
|
<math>~\biggl( \frac{2 \xi^2}{3\cdot 5} \biggr) \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A - \theta^{n+1} \, . </math> |
Similarly, in the case of <math>~n = 5</math> structures,
|
<math>~\theta^{n+1}</math> |
<math>~=</math> |
<math>~ (1 + \ell^2)^{-3} </math> |
|
<math>~\Rightarrow ~~~\biggl( \frac{2^3}{3} \ell^{3} \biggr) \biggl[ \mathfrak{f}_A - \theta^{n+1} \biggr]</math> |
<math>~=</math> |
<math>~ [ \tan^{-1}(\ell ) + \ell (\ell^4-1) (1+\ell^2)^{-3} ] - \biggl( \frac{2^3}{3} \ell^{3} \biggr) (1 + \ell^2)^{-3} </math> |
|
|
<math>~=</math> |
<math>~ \tan^{-1}(\ell ) + \ell \biggl(\ell^4-\frac{8}{3}\ell^2 - 1 \biggr) (1+\ell^2)^{-3} \, . </math> |
But, we also have shown that,
|
<math>~\biggl( \frac{2^4}{5} \cdot \ell^{5} \biggr) \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \, . </math> |
Hence, we see that,
|
<math>~\biggl( \frac{2\cdot 3}{5} \cdot \ell^{2} \biggr) \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A - \theta^{n+1} </math> |
|
<math>~\Rightarrow ~~~~\biggl( \frac{2\xi^2}{5} \biggr) \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A - \theta^{n+1} \, . </math> |
This is pretty amazing! Both examples produce almost exactly the same relationship between the two structural form factors, <math>~\mathfrak{f}_A</math> and <math>~\mathfrak{f}_W</math>. I think that we are well on our way toward nailing down the generic, analytic relationship and, in turn, a generally applicable mass-radius relationship for pressure-truncated polytropic configurations.
Okay … here is the final piece of information. In the case of isolated polytropes, we know that the correct expressions for the structural form factors are as summarized in the following table:
|
Structural Form Factors for Isolated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
We notice, from this, that the ratio,
|
<math>\frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} </math> |
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\tilde\xi} \cdot \frac{5-n}{3^2\cdot 5} \biggl[ \frac{\xi}{\Theta^'} \biggr]^{2}_{\tilde\xi} </math> |
|
|
<math>~=</math> |
<math> \frac{(n+1)\tilde\xi^2 }{3\cdot 5} \, . </math> |
Even in the case of the two pressure-truncated polytropes, analyzed above, this ratio proves to give the correct prefactor on <math>~\mathfrak{f}_W</math>. So we suspect that the universal relationship between the two form factors is,
|
<math>~\biggl[ \frac{(n+1) \xi^2 }{3\cdot 5} \biggr] \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A - \theta^{n+1} \, . </math> |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |