BiPolytrope with <math>n_c = 5</math> and <math>n_e=1</math>

Here we construct a bipolytrope in which the core has an <math>n_c=5</math> polytropic index and the envelope has an <math>n_c=1</math> polytropic index. This system is particularly interesting because the entire structure can be described by closed-form, analytic expressions. As far as I have been able to determine, this analytic structural model has not previously been published in a refereed, archival journal (author: Joel E. Tohline, March 30, 2013). In deriving the properties of this model, we will follow the general solution steps for constructing a bipolytrope that we have outlined elsewhere.

Steps 2 & 3

Based on the discussion presented elsewhere of the structure of an isolated <math>n=5</math> polytrope, the core of this bipolytrope will have the following properties:

<math> \theta(\xi) = \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-1/2} ~~~~\Rightarrow ~~~~ \theta_i = \biggl[ 1 + \frac{1}{3}\xi_i^2 \biggr]^{-1/2} ; </math>

<math> \frac{d\theta}{d\xi} = - \frac{\xi}{3}\biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3/2} ~~~~\Rightarrow ~~~~ \biggl(\frac{d\theta}{d\xi}\biggr)_i = - \frac{\xi_i}{3}\biggl[ 1 + \frac{1}{3}\xi_i^2 \biggr]^{-3/2} \, . </math>

The first zero of the function <math>\theta(\xi)</math> and, hence, the surface of the corresponding isolated <math>n=5</math> polytrope is located at <math>\xi_s = \infty</math>. Hence, the interface between the core and the envelope can be positioned anywhere within the range, <math>0 < \xi_i < \infty</math>.

Step 4: Throughout the core (<math>0 \le \xi \le \xi_i</math>)

Specify: <math>K_c</math> and <math>\rho_0 ~\Rightarrow</math>
<math>\rho</math>	<math>=</math>	<math>\rho_0 \theta^{n_c}</math>	<math>=</math>	<math>\rho_0 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2}</math>
<math>P</math>	<math>=</math>	<math>K_c \rho_0^{1+1/n_c} \theta^{n_c + 1}</math>	<math>=</math>	<math>K_c \rho_0^{6/5} \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3}</math>
<math>r</math>	<math>=</math>	<math>\biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{1/2} \rho_0^{(1-n_c)/(2n_c)} \xi</math>	<math>=</math>	<math>\biggl[ \frac{K_c}{G\rho_0^{4/5}} \biggr]^{1/2} \biggl(\frac{3}{2\pi}\biggr)^{1/2} \xi</math>
<math>M_r</math>	<math>=</math>	<math>4\pi \biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{3/2} \rho_0^{(3-n_c)/(2n_c)} \biggl(-\xi^2 \frac{d\theta}{d\xi} \biggr)</math>	<math>=</math>	<math>\biggl[ \frac{K_c^3}{G^3 \rho_0^{2/5} } \biggr]^{1/2} \biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]</math>

Step 5: Interface Conditions

			Setting <math>n_c=5</math>, <math>n_e=1</math>, and <math>\phi_i = 1 ~~~~\Rightarrow</math>
<math>\frac{\rho_e}{\rho_0}</math>	<math>=</math>	<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{n_c}_i \phi_i^{-n_e}</math>	<math>=</math>	<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i </math>
<math>\biggl( \frac{K_e}{K_c} \biggr) </math>	<math>=</math>	<math>\rho_0^{1/n_c - 1/n_e}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-(1+1/n_e)} \theta^{1 - n_c/n_e}_i</math>	<math>=</math>	<math>\rho_0^{-4/5}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-4}_i</math>
<math>\frac{\eta_i}{\xi_i}</math>	<math>=</math>	<math>\biggl[ \frac{n_c + 1}{n_e+1} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{(n_c-1)/2} \phi_i^{(1-n_e)/2}</math>	<math>=</math>	<math>3^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{2}</math>
<math>\biggl( \frac{d\phi}{d\eta} \biggr)_i</math>	<math>=</math>	<math>\biggl[ \frac{n_c + 1}{n_e + 1} \biggr]^{1/2} \theta_i^{- (n_c + 1)/2} \phi_i^{(n_e+1)/2} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math>	<math>=</math>	<math>3^{1/2} \theta_i^{- 3} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math>

Step 6: Envelope Solution

The most general solution to the <math>n=1</math> Lane-Emden equation is,

<math> \phi = A \biggl[ \frac{\sin(\eta - B)}{\eta} \biggr] \, , </math>

where <math>A</math> and <math>B</math> are constants. The first derivative of this function is,

<math> \frac{d\phi}{d\eta} = \frac{A}{\eta^2} \biggl[ \eta\cos(\eta-B) - \sin(\eta-B) \biggr] \, . </math>

From Step 5, above, we know the value of the function, <math>\phi</math> and its first derivative at the interface; specifically,

<math> \phi_i = 1~~~~\mathrm{and} ~~~~\biggl( \frac{d\phi}{d\eta}\biggr)_i =3^{1/2} \theta_i^{- 3} \biggl( \frac{d\theta}{d\xi} \biggr)_i~~~~ \mathrm{at}~~~~\eta_i =3^{1/2} \xi_i \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{2}</math>

From this information we can determine the constants <math>A</math> and <math>B</math>; specifically,

<math> \eta_i - B = \tan^{-1}(\Lambda_i^{-1}) = \frac{\pi}{2}- \tan^{-1}(\Lambda_i) \, , </math>

<math> A = \frac{\phi_i \eta_i}{\sin(\eta_i - B)} = \phi_i \eta_i (1 + \Lambda_i^2)^{1/2} \, , </math>

where,

<math> \Lambda_i = \frac{1}{\eta_i} + \frac{1}{\phi_i} \biggl(\frac{d\phi}{d\eta}\biggr)_i \, . </math>

Step 7

The surface will be defined by the location, <math>\eta_s</math>, at which the function <math>\phi(\eta)</math> first goes to zero, that is,

<math> \eta_s = \pi + B = \frac{\pi}{2} + \eta_i + \tan^{-1}(\Lambda_i) \, . </math>

Step 8: Throughout the envelope (<math>\eta_i \le \eta \le \eta_s</math>)

					Knowing: <math>K_e/K_c</math> and <math>\rho_e/\rho_0</math> from Step 5 <math>\Rightarrow</math>
<math>\rho</math>	<math>=</math>	<math>\rho_e \phi^{n_e}</math>	<math>=</math>	<math>\rho_0 \biggl(\frac{\rho_e}{\rho_0}\biggr) \phi</math>	<math>=</math>	<math>\rho_0 \biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i \phi</math>
<math>P</math>	<math>=</math>	<math>K_e \rho_e^{1+1/n_e} \phi^{n_e + 1}</math>	<math>=</math>	<math>K_c \rho_0^{6/5} \biggl(\frac{K_e \rho_0^{4/5}}{K_c}\biggr) \biggl(\frac{\rho_e}{\rho_0}\biggr)^{2} \phi^{2}</math>	<math>=</math>	<math>K_c \rho_0^{6/5} \theta^{6}_i \phi^{2}</math>
<math>r</math>	<math>=</math>	<math>\biggl[ \frac{(n_e + 1)K_e}{4\pi G} \biggr]^{1/2} \rho_e^{(1-n_e)/(2n_e)} \eta</math>	<math>=</math>	<math>\biggl[ \frac{K_c}{G \rho_0^{4/5}} \biggr]^{1/2} \biggl( \frac{K_e \rho_0^{4/5}}{K_c} \biggr)^{1/2} (2\pi)^{-1/2}\eta</math>	<math>=</math>	<math>\biggl[ \frac{K_c}{G \rho_0^{4/5}} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta</math>
<math>M_r</math>	<math>=</math>	<math>4\pi \biggl[ \frac{(n_e + 1)K_e}{4\pi G} \biggr]^{3/2} \rho_e^{(3-n_e)/(2n_e)} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math>	<math>=</math>	<math>\biggl[ \frac{K_c^3}{G^3 \rho_0^{2/5}} \biggr]^{1/2} \biggl( \frac{K_e \rho_0^{4/5}}{K_c} \biggr)^{3/2} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math>	<math>=</math>	<math>\biggl[ \frac{K_c^3}{G^3 \rho_0^{2/5}} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math>

Examples

Normalization

The dimensionless variables used in Tables 1 & 2 are defined as follows:

<math>\rho^*</math>	<math>\equiv</math>	<math>\frac{\rho}{\rho_0}</math>	;	<math>r^*</math>	<math>\equiv</math>	<math>\frac{r}{[K_c^{1/2}/(G^{1/2}\rho_0^{2/5})]}</math>
<math>P^*</math>	<math>\equiv</math>	<math>\frac{P}{K_c\rho_0^{6/5}}</math>	;	<math>M_r^*</math>	<math>\equiv</math>	<math>\frac{M_r}{[K_c^{3/2}/(G^{3/2}\rho_0^{1/5})]}</math>
<math>H^*</math>	<math>\equiv</math>	<math>\frac{H}{K_c\rho_0^{1/5}}</math>	.

Parameter Values

Table 1: Properties of <math>n_c=5</math>, <math>n_e=1</math>, BiPolytrope Having Various Interface Locations, <math>\xi_i</math>
File:BiPolytropeParametersV01.xml

Parameter	<math>\xi_i</math>	0.5	1.0	3.0	10
<math>\theta_i</math>	<math>\biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-1/2}</math>	0.96077	0.86603	0.50000
<math>-\biggl(\frac{d\theta_i}{d\xi}\biggr)_i</math>	<math>\frac{1}{3} \xi_i \biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-3/2}</math>	0.14781	0.21651	0.12500
<math>r^_\mathrm{core} \equiv r^_i</math>	<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi_i</math>	0.34549	0.69099	2.07297
<math>\rho^_i \biggr\|_c = \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \rho^_i \biggr\|_e</math>	<math>\biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-5/2}</math>	0.81864	0.48714	0.03125
<math>P^*_i</math>	<math>\biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-3}</math>	0.78653	0.42188	0.01563
<math>H^_i \biggr\|_c = \frac{n_c+1}{n_e+1} \biggl( \frac{\mu_e}{\mu_c} \biggr) H^_i \biggr\|_e</math>	<math>6 \biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-1/2}</math>	5.76461	5.19615	3.00000
<math>M^*_\mathrm{core}</math>	<math>\biggl( \frac{6}{\pi}\biggr)^{1/2} (\xi_i \theta_i)^3</math>	0.15320	0.89762	4.66417
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1}\eta_i</math>	<math>\sqrt{3} ~\theta_i^2 \xi_i</math>	0.79941	1.29904	1.29904
<math>-\biggl( \frac{d\phi}{d\eta} \biggr)_i</math>	<math>\sqrt{3} ~\theta_i^{-3} \biggl( - \frac{d\theta}{d\xi} \biggr)_i = \frac{\xi_i}{\sqrt{3}}</math>	0.28868	0.57735	1.73205
<math>\Lambda_i</math>	<math>\frac{1}{\eta_i} + \biggl( \frac{d\phi}{d\eta} \biggr)_i</math>	0.96225	0.19245	-0.96225
<math>A</math>	<math>\eta_i (1 + \Lambda_i^2)^{1/2}</math>	1.10940	1.32288	1.80278
<math>B</math>	<math>\eta_i - \frac{\pi}{2} + \tan^{-1}( \Lambda_i)</math>	- 0.00523	-0.08163	-1.03792
<math>\eta_s</math>	<math>\pi + B</math>	3.13637	3.05996	2.10367
<math>- \biggl( \frac{d\phi}{d\eta} \biggr)_s</math>	<math>\frac{A}{\eta_s}</math>	0.35372	0.43232	0.85697
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \cdot \biggl[ R^* \equiv r^*_s \biggr]</math>	<math>\frac{\eta_s}{\sqrt{2\pi} ~\theta_i^2}</math>	1.35550	1.62766	3.35697
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^2 M^*_\mathrm{tot}</math>	<math>\biggl(\frac{2}{\pi}\biggr)^{1/2} \theta_i^{-1} \biggl( -\eta^2 \frac{d\phi}{d\eta} \biggr)_s = \biggl(\frac{2}{\pi}\biggr)^{1/2} \frac{A\eta_s}{\theta_i}</math>	2.88959	3.72945	6.05187
<math>\biggl(\frac{\mu_e}{\mu_c}\biggr)^{-2} \cdot \biggl[ q \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} \biggr]</math>	<math>\sqrt{3} ~\biggl( \frac{\xi_i^3 \theta_i^4}{A\eta_s} \biggr)</math>	0.05302	0.24068	0.77070
<math>\biggl(\frac{\mu_e}{\mu_c}\biggr)^{-1} \cdot \biggl[ \frac{r_\mathrm{core}}{R} \biggr]</math>	<math>\sqrt{3}~\biggl[\frac{\xi_i \theta_i^2}{\eta_s}\biggr]</math>	0.25488	0.42453	0.61751

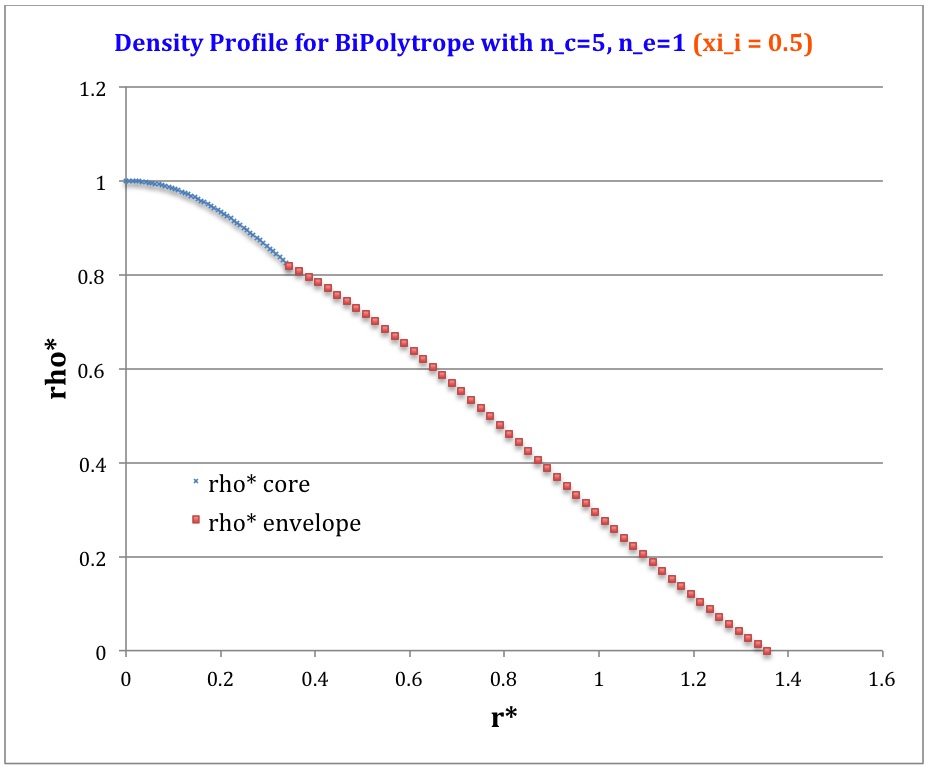
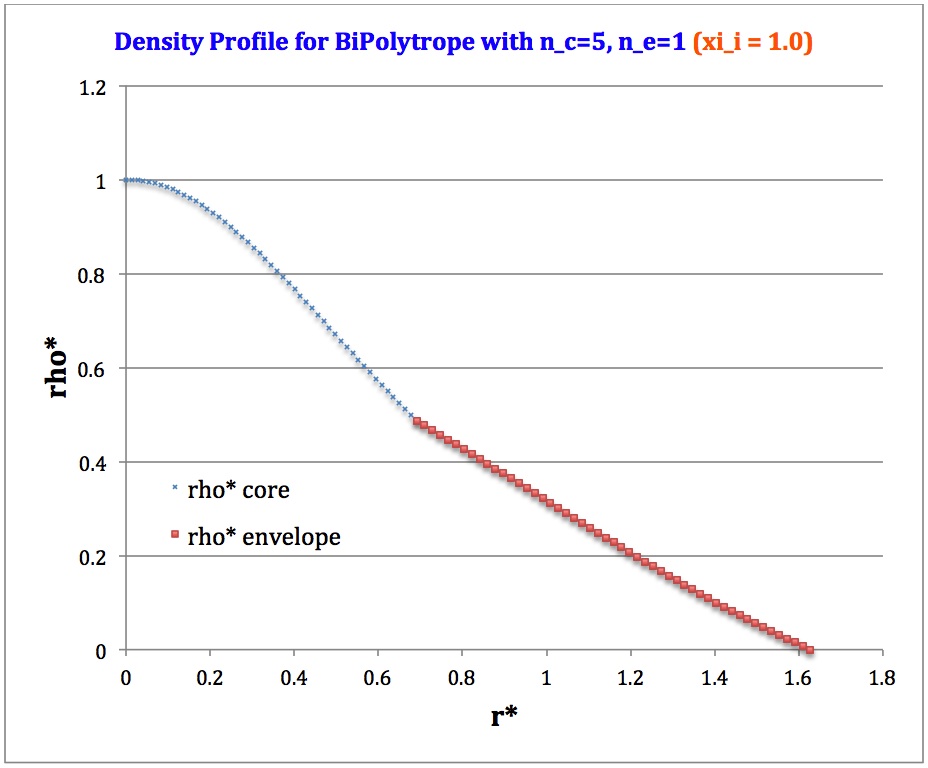
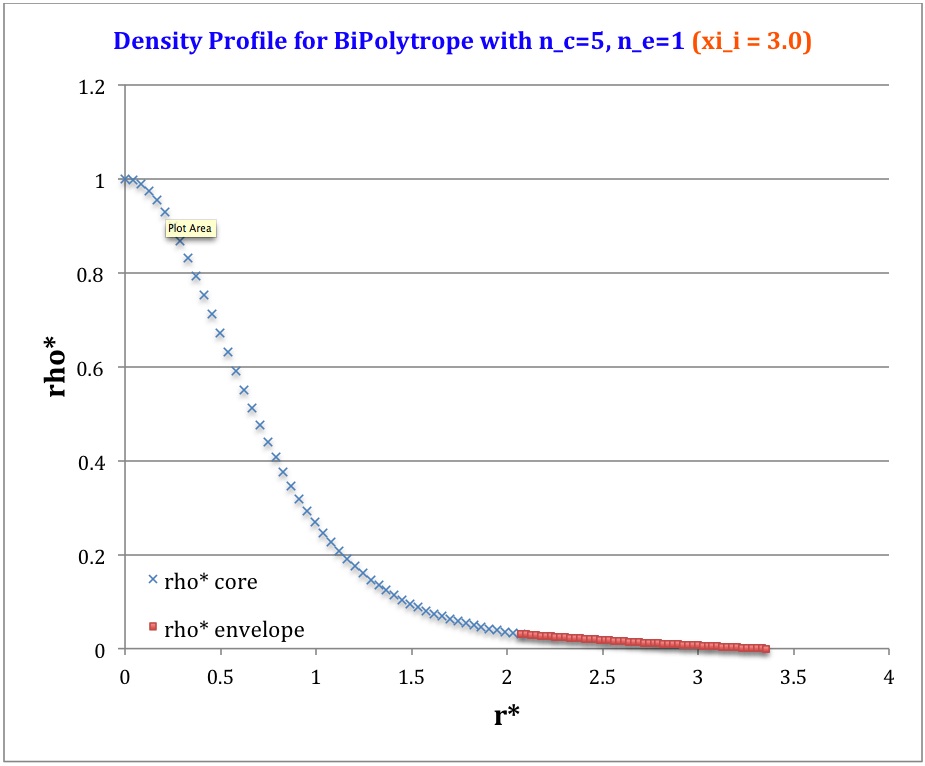
Profile

Table 2: Radial Profile of Various Physical Variables

Variable	Throughout the Core <math>0 \le \xi \le \xi_i</math>	Throughout the Envelope^† <math>\eta_i \le \eta \le \eta_s</math>	Plotted Profiles
			<math>\xi_i = 0.5</math>	<math>\xi_i = 1.0</math>	<math>\xi_i = 3.0</math>
<math>r^*</math>	<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi</math>	<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta</math>
<math>\rho^*</math>	<math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2}</math>	<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i \phi(\eta)</math>
<math>P^*</math>	<math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3}</math>	<math>\theta^{6}_i [\phi(\eta)]^{2}</math>
<math>M_r^*</math>	<math>\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]</math>	<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math>
^†In order to obtain the various envelope profiles, it is necessary to evaluate <math>\phi(\eta)</math> and its first derivative using the information presented in Step 6, above.