Maclaurin Spheroid Sequence

Detailed Force Balance Conditions

Figure 1

Solid black curve also may be found as:

Fig. 5 (p. 79) of [EFE];
Fig. 7.2 (p. 173) of [ST83]

The essential structural elements of each Maclaurin spheroid model are uniquely determined once we specify the system's axis ratio, <math>~c/a</math>, or by the system's meridional-plane eccentricity, <math>~e</math>, where

<math>~\equiv</math>

<math>~\biggl[1 - \biggl(\frac{c}{a}\biggr)^2\biggr]^{1 / 2} \, ,</math>

which varies from e = 0 (spherical structure) to e = 1 (infinitesimally thin disk). According to our accompanying derivation, for a given choice of <math>~e</math>, the square of the system's equilibrium angular velocity is,

<math> ~ \omega_0^2 </math>

<math> 2\pi G \rho \biggl[ A_1 - A_3 (1-e^2) \biggr] \, , </math>

where,

<math> ~A_1 </math>	<math> ~= </math>	<math> \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} - (1-e^2)^{1/2} \biggr](1-e^2)^{1/2} \, , </math>
<math> ~A_3 </math>	<math> ~= </math>	<math> \frac{2}{e^2} \biggl[(1-e^2)^{-1/2} -\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{1/2} \, . </math>

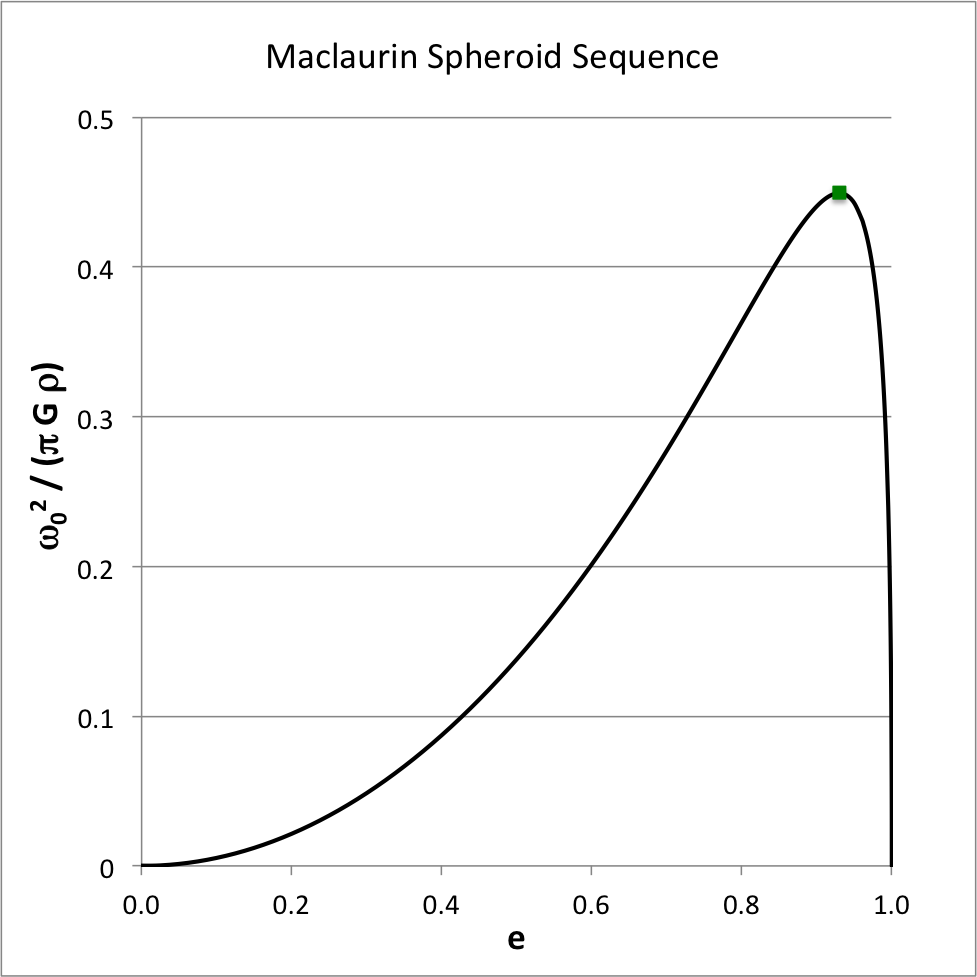
Figure 1 shows how the square of the angular velocity varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~\pi G\rho</math>, it is understood that the density of the configuration is held fixed as the eccentricity is varied. The small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides:

<math>~\biggl[ e, \frac{\omega_0^2}{\pi G \rho} \biggr]</math>	<math>~\equiv</math>	<math>~\biggl[ 0.92995, 0.449331 \biggr] \, .</math>
[EFE], §32, p. 80, Eqs. (9) & (10)

Alternate Sequence Diagrams

The total angular momentum of each uniformly rotating Maclaurin spheroid is given by the expression,

<math>~I \omega_0 \, ,</math>

where, the moment of inertia <math>~(I)</math> and the total mass <math>~(M)</math> of a uniform-density spheroid are, respectively,

<math>~\biggl(\frac{2}{5}\biggr) M a^2 \, ,</math>

and,

<math>~\biggl( \frac{4\pi}{3} \biggr) \rho a^2c \, .</math>

Hence, we have,

<math>~L^2</math>	<math>~=</math>	<math>~ \frac{2^2 M^2 a^4}{5^2} \biggl[ A_1 - A_3 (1-e^2) \biggr] 2\pi G \biggl[ \frac{3}{2^2\pi} \cdot \frac{M}{a^2c} \biggr]</math>
	<math>~=</math>	<math>~ \frac{6GM^3 {\bar{a}}}{5^2} \biggl[ A_1 - A_3 (1-e^2) \biggr]\biggl(\frac{a}{c}\biggr)^{4/3} </math>
<math>~\Rightarrow ~~~ \frac{L}{(GM^3\bar{a})^{1 / 2}}</math>	<math>~=</math>	<math>~ \frac{6^{1 / 2}}{5} \biggl[ A_1 - A_3 (1-e^2) \biggr]^{1 / 2}(1 - e^2)^{-1 / 3} \, ,</math>
[EFE], §32, p. 78, Eq. (7) [T78], §4.5, p. 86, Eq. (54)
where, <math>~\bar{a} \equiv (a^2 c)^{1 / 3} \, .</math>

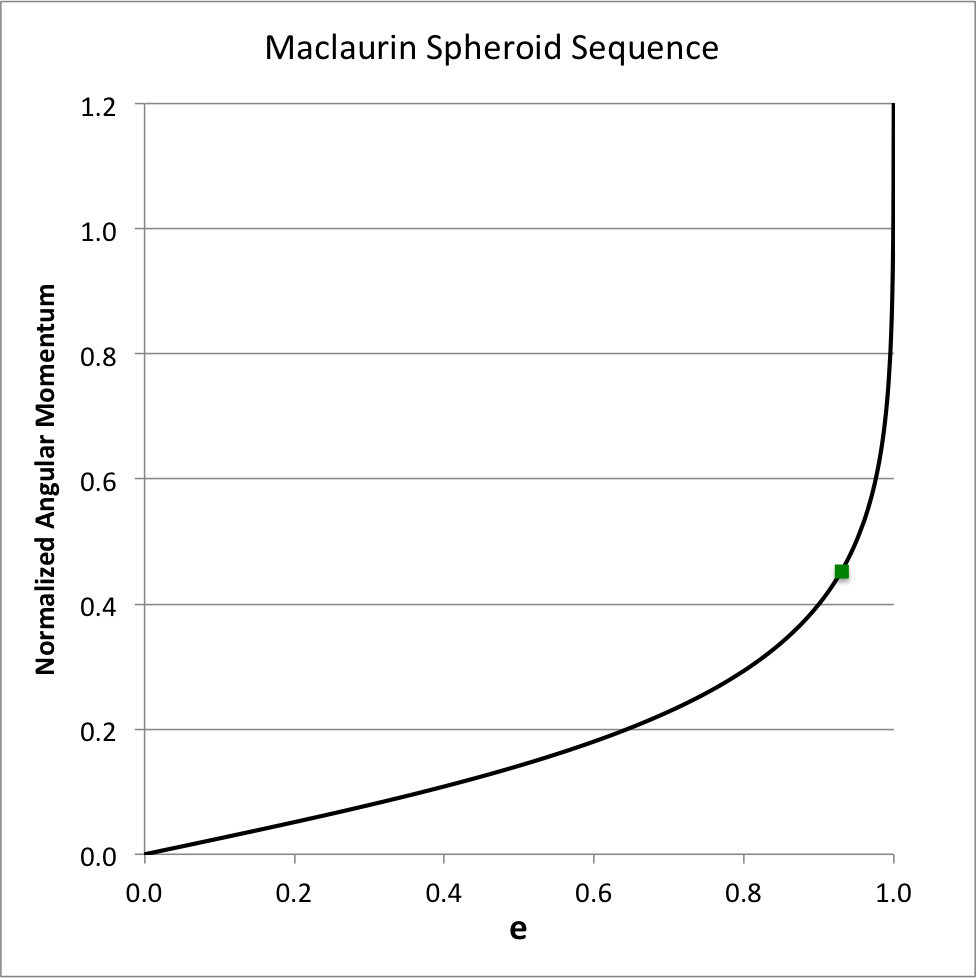
Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a maximum value of 1.2, the plot masks this asymptotic behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence.

Figure 2		Figure 3

Solid black curve also may be found as: Fig. 6 (p. 79) of [EFE]; Fig. 7.3 (p. 174) of [ST83]		This solid black curve also appears in: Fig. 3 (p. 1134) of Eriguchi & Hachisu (1983) Fig. 4 (p. 4507) of Basillais & Huré (2019)

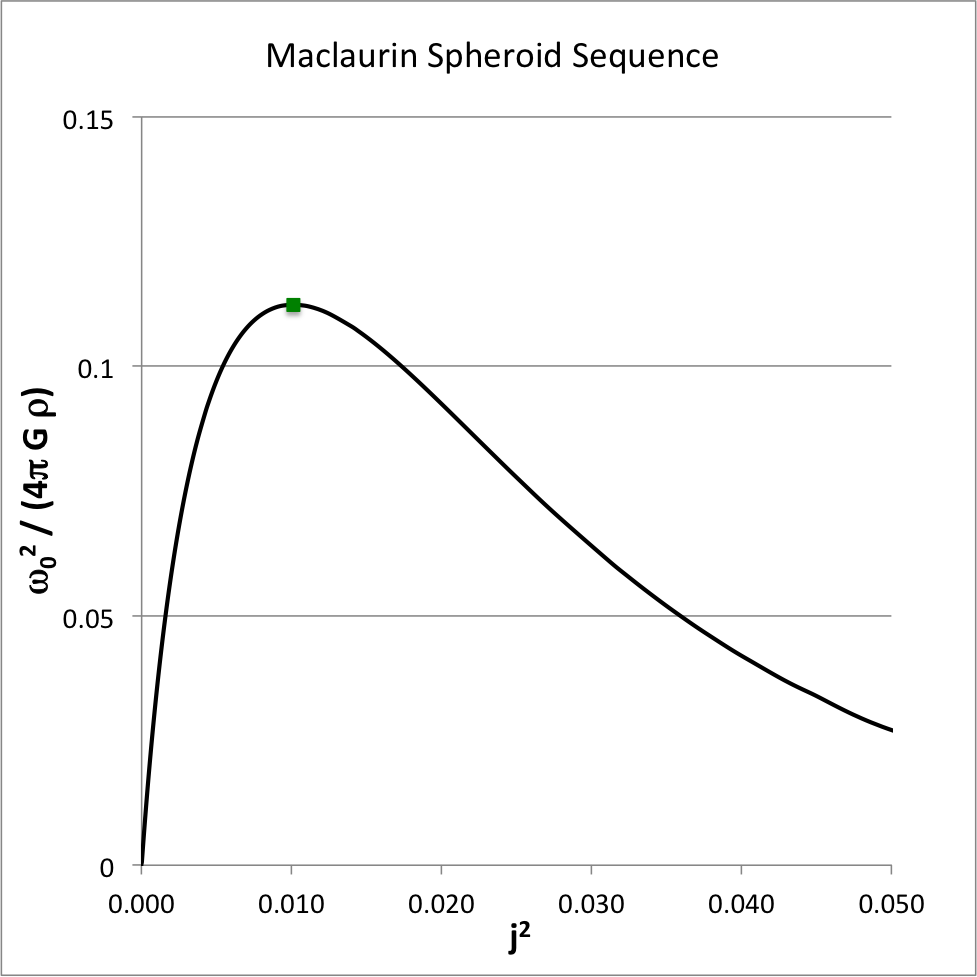
Figure 3 shows how the square of the angular velocity varies with the square of the angular momentum for models along the Maclaurin spheroid sequence. In generating this plot, following the lead of Eriguchi & Hachisu (1983), we have divided the square of the angular velocity by an additional factor of four, and we have adopted a slightly different angular-momentum normalization, namely,

<math>~\equiv</math>

<math>~

\biggl( \frac{3}{2^8 \pi^4}  \biggr)^{1/6}  \frac{L}{(GM^3\bar{a})^{1 / 2}} \, .

</math>

As above, the small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides:

<math>~\biggl[ j^2, \frac{\omega_0^2}{4\pi G \rho} \biggr]</math>

<math>~\equiv</math>

<math>~\biggl[ 0.010105, 0.112333 \biggr] \, .</math>

User:Tohline/Apps/MaclaurinSpheroidSequence

Contents

Maclaurin Spheroid Sequence

Detailed Force Balance Conditions

Alternate Sequence Diagrams

See Also

Navigation menu

Search