User:Tohline/SSC/Structure/Lane1870
Lane's 1870 Work

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
In what follows, text presented in a dark green font (and/or, as indicated, each equation) has been copied verbatim from a scientifically impactful 1870 article by J. Homer Lane. Note that we have broken the article into separate segments in order to facilitate the insertion of interspersed comments. Our accompanying discussion of Polytropic Spheres shows how this groundbreaking physical/mathematical model developed by Lane to probe the interior structure of the Sun — encapsulated in what is now commonly referred to as the Lane-Emden equation — provides a tool for understanding stars that have a wide range of structural properties.
SEGMENT I
|
J. H. Lane (1870), The American Journal of Science and Arts, Vol. 50, pp. 57 - 74: On the Theoretical Temperature of the Sun under the Hypothesis of a Gaseous Mass Maintaining Its Volume by Its Internal Heat and Depending on the Laws of Gases Known to Terrestrial Experiment SEGMENT I (beginning on p. 57)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
[Read (by J. Homer Lane at age 49) before the National Academy of Sciences at the session of April 13-16, 1869.] Many years have passed since the suggestion was thrown out by Helmholtz, and afterwards by others, that the present volume of the sun is maintained by his internal heat, and may become less in time. Upon this hypothesis it was proposed to account for the renewal of the heat radiated from the sun, by means of the mechanical power of the sun's mass descending toward his center. Calculations made by Prof. Pierce, and I believe by others, have shown that this provides a supply of heat far greater than it is possible to attribute to the meteoric theory of Prof. Wm. Thomson, which, I understand, has been abandoned by Prof. Thomson himself as not reconcilable with astronomical facts. Some years ago the question occurred to me in connection with this theory of Helmholtz whether the entire mass of the sun might not be a mixture of transparent gases, and whether Herschel's clouds might not arise from the precipitation of some of these gases, say carbon, near the surface, with their revaporization when fallen or carried into the hotter subjacent layers of atmosphere beneath; the circulation necessary for the play of this Espian theory being of course maintained by the constant disturbance of equilibrium due to the loss of heat by radiation from the precipitated clouds. Prof. Espy's theory of storms I first became acquainted with more than twenty years ago from lectures delivered by himself, and, original as I suppose it to be, and well supported as it is in the phenomena of terrestrial meteorology, I have long thought that Prof. Espy's labors deserve a more general recognition than they have received abroad. It is not surprising, therefore, in a time when the constitution of the sun was exciting so much discussion, that the above suggestions should have occurred to myself before I became aware of the very similar, and in the main identical, views of Prof. Faye, put forth in the Comptes Rendus. I sought to determine how far such a supposed constitution of the sun could be made to connect with the laws of the gases as known to us in terrestrial experiments at common temperatures. Some calculations based upon conjectures of the highest temperature and least density thought supposable at the sun's photosphere led me to the conclusion that it was extremely difficult if not impossible, to make out the connection in a credible manner. Nevertheless, I mentioned my ideas to Prof. Henry, Secretary of the Smithsonian Institution, when he immediately referred me to a number of the Comptes Rendus, then recently received, containing Faye's exposition of his theory. Of course nothing is further from my purpose than to make any kind of claim to any thing in that publication. After becoming acquainted with his labors I still regarded the theory as seriously lacking, in its physical or mechanical aspect, the direct support of confirmatory observations, and even as being subject to grave difficulty in that direction. In this attitude I allowed the subject to rest until my friend Dr. Craig, in charge of the Chemical Laboratory of the Surgeon General's office, without any knowledge of Faye's memoir, or of my own suggestions previously made to Prof. Henry and another scientific friend, fell upon the same ideas of the sun's constitution, availing himself, precisely as I had done, of Espy's theory of storms. Dr. Craig's ideas were communicated to a company of scientific gentlemen early last spring, and soon after, Prof. Newcomb, of the U. S. Naval Observatory, entered into a general survey of the nebular hypothesis. These communications of Dr. Craig and Prof. Newcomb led me to enter into a renewed examination of the mechanical embarrassment under which I had believed the theory to labor. Not any longer relying on my first rough estimate based on assumed high temperatures at the photosphere, the question was now inverted. Assuming the gaseous constitution, and assuming the laws expressed in Poisson's formulæ, known to govern the constitution of gases at common temperatures and densities, what shall we find to be the temperatures and densities corresponding to the observed volume of the sun supposing it were composed of some known gas such as hydrogen, or supposing it to be composed of such a mixture of gases as would be represented by common air. Pure hydrogen will, of course, give us the lowest temperature of all known substances, under the general hypothesis. The question was resolved, and the results were communicated in graphical and numerical form in May or June last to two or three scientific friends, but their publication has been delayed by an unavoidable absence of several months from home. Premising that the unit of density shall correspond to a unit of mass in the cube of the unit of length, the unit of force to the force of terrestrial gravity in the unit of mass, and the unit of pressure or elasticity in the gas to the unit of force on a surface equal to the square of the unit of length:
The condition of equilibrium between the gravitating force of a thin horizontal layer of gas whose thickness is <math>~dr</math>, and the difference of elastic force between its lower and upper surfaces is expressed by the equation,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
We see that, drawing upon his background in meteorology, Lane is suggesting that the radial dependence of various internal properties of the Sun is governed by the key integro-differential equation that is now commonly referred to as a statement of,
where,
Our derivation of this mathematical statement of hydrostatic balance has been tagged, Technique 1, in our accompanying discussion of various solution strategies.
SEGMENT II
|
J. H. Lane (1870), The American Journal of Science and Arts, Vol. 50, pp. 57 - 74: On the Theoretical Temperature of the Sun under the Hypothesis of a Gaseous Mass Maintaining Its Volume by Its Internal Heat and Depending on the Laws of Gases Known to Terrestrial Experiment SEGMENT II (beginning on p. 59)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Under the hypothesis that the law of Mariotte and the law of Poisson prevail throughout the whole mass, and that this mass is in convective equilibrium, we have
<math>~t_1</math> representing the value of <math>~t</math> in the part of the mass where the density is a unit. In this last expression, the parameter <math>~k</math> that appears in the exponent represents the ratio of specific heat of a gas under constant pressure to its specific heat under constant volume. Instead of <math>~k</math>, it is more common in modern notation to use, <math>~\gamma_g\equiv c_P/c_V</math>. The theoretical difficulties which, if the supply of solar heat is to be kept up by the potential due to the mutual approach of the parts of the sun's mass consequent on the loss of heat by radiation, come in when we suppose a material departure from these laws of Mariotte and of Poisson at the extreme temperatures and pressures in the sun's body, or how far such difficulties intervene, will be considered further on. By means of the constant value of <math>~\sigma</math>, and the value of <math>~t</math> given in (1), the above differential equation is transformed into
the integral of which gives
in which <math>~\rho_0</math> is the value of <math>~\rho</math> at the sun's center. We have also,
If now we put
we shall have
in which
and equation (2) becomes
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Drawing upon Technique 2 from our discussion of various solution strategies, in a separate chapter we have derived what is now commonly referred to as the,
Polytropic Lane-Emden Equation
|
<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math> |
where, given that <math>~n = (\gamma_\mathrm{g}-1)^{-1}</math> and <math>~K_n = P_c \rho_c^{-(n+1)/n}</math>, we have,
| Modern Notation |
Lane's Notation |
|||||
|
<math>~\Theta_H</math> |
<math>~=</math> |
<math>~\biggl( \frac{\rho}{\rho_c} \biggr)^{1/n}</math> |
<math>~\Theta_H</math> |
<math>~=</math> |
<math>~\biggl( \frac{\rho}{\rho_0} \biggr)^{k-1}</math> |
|
and the dimensionless radial coordinate, <math>~\xi</math>, is defined via the relation,
| Modern Notation |
Lane's Notation |
|||||
|
<math>~r</math> |
<math>~=</math> |
<math>~\biggl[\frac{(n+1)K_n}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \xi</math> |
|
|
|
|
|
|
<math>~=</math> |
<math>~\biggl[\frac{\gamma_\mathrm{g}}{4\pi G(\gamma_\mathrm{g}-1)} \cdot \frac{P_c}{\rho_c^2} \biggr]^{1/2} \xi</math> |
<math>~r</math> |
<math>~=</math> |
<math>~\biggl[\frac{k}{4\pi G(k-1)} \biggl(\frac{GM_\oplus}{R_\oplus^2}\biggr)\frac{\sigma t_c}{\rho_c} \biggr]^{1/2} \xi</math> |
|
|
|
|
|
|
<math>~=</math> |
<math>~\biggl[\frac{k}{4\pi (k-1)} \biggl(\frac{M_\oplus}{R_\oplus^2}\biggr)\frac{\sigma t_1 \rho_c^{k-1}}{\rho_c} \biggr]^{1/2} \xi</math> |
|
Comparing this last expression with Lane's equation (4), it is therefore clear that Lane's dimensionless radial function, <math>~x</math>, is identical to the now more commonly used dimensionless radial function, <math>~\xi</math>. Note, as well, that Integrating the Polytropic Lane-Emden Equation once gives,
|
<math>~\xi^2 \frac{d\Theta_H}{d\xi}</math> |
<math>~=</math> |
<math>~- \int_0^\xi \xi^2 \Theta_H^n d\xi</math> |
|
<math>~\Rightarrow ~~~ \xi^2 \frac{d}{d\xi}\biggl( \frac{\rho}{\rho_0} \biggr)^{k-1}</math> |
<math>~=</math> |
<math>~- \int_0^\xi \xi^2 \biggl( \frac{\rho}{\rho_0} \biggr) d\xi</math> |
|
|
<math>~=</math> |
<math>~- \mu_\mathrm{Lane} \, ,</math> |
where the function, <math>~\mu_\mathrm{Lane}</math>, is as defined by Lane's equation (6); and integrating a second time gives,
|
<math>~\int_{\rho_0}^\rho d\biggl( \frac{\rho}{\rho_0} \biggr)^{k-1}</math> |
<math>~=</math> |
<math>~- \int_0^\xi \frac{\mu_\mathrm{Lane}}{\xi^2} d\xi</math> |
|
<math>~\Rightarrow ~~~ 1 - \biggl( \frac{\rho}{\rho_0} \biggr)^{k-1}</math> |
<math>~=</math> |
<math>~+ \int_0^\xi \frac{\mu_\mathrm{Lane}}{\xi^2} d\xi \, ,</math> |
which is identically Lane's equation (7). It is therefore clear that Lane's equation (7) provides a mathematical model of the same stellar-interiors problem as — and is simply an integrated form of — the 2nd-order ODE that now customarily carries his name (along with Emden's).
SEGMENT III
|
J. H. Lane (1870), The American Journal of Science and Arts, Vol. 50, pp. 57 - 74: On the Theoretical Temperature of the Sun under the Hypothesis of a Gaseous Mass Maintaining Its Volume by Its Internal Heat and Depending on the Laws of Gases Known to Terrestrial Experiment SEGMENT III (pp. 60 - 64)
| |||||||||||||||
|
In equations (6) and (7) it is plain that upon the value of <math>~k</math> alone depends: first the form of the curve that expresses the value of <math>~\rho/\rho_0</math> for each value of <math>~x</math>; secondly, the value of the upper limit of <math>~x</math> corresponding to <math>~\rho/\rho_0 = 0</math> [henceforth this value of the dimensionless radius at the surface will be labeled <math>~x'</math>]; and thirdly, the corresponding value of <math>~\mu</math> [henceforth this value of the dimensionless total mass will be labeled <math>~\mu'</math>]. These limiting, or terminal, value of <math>~x</math> and <math>~\mu</math>, cannot be found except by calculating the curve, for equations (6) and (7) seem incapable of being reduced to a complete general integral. But when these values have been found for any proposed value of <math>~k</math>, they may be introduced once for all into equations (4) and (5), from which the values of <math>~\rho_0</math>, and <math>~\sigma t_1</math>, are at once deduced. I have made these calculations for two different assumed values of <math>~k</math>, viz., <math>~k = 1.4</math> … and <math>~k = 1\tfrac{2}{3}</math> …
Upon [d]etermination of the curve of density for <math>~k = 1.4</math> … we find
And a determination of the [c]urve of density for <math>~k = 1\tfrac{2}{3}</math> … gives us
|
In an effort to acknowledge the strikingly high precision with which Lane was able to determine the "curves of density" for this pair of models, the following table shows the values of <math>~x'</math> and <math>~\mu'</math> taken directly from Lane's publication (see the table cells with light green backgrounds) along with the corresponding values of the surface radius and total mass as has been calculated and published independently by Emden (1907) and by Horedt (2004). (Additional details from the published tabulations of these two authors can be found in the subsections that follow.)
| <math>~k = 1\tfrac{2}{3} ~~\Rightarrow ~~n = \tfrac{3}{2}</math> | <math>~k = 1.4 ~~\Rightarrow ~~n = \tfrac{5}{2}</math> | |||||
| <math>~x' = \xi_1</math> (radius) |
<math>~\mu'</math> (total mass) |
<math>~\frac{\rho_c}{\bar\rho} = \frac{(x')^3}{3\mu'}</math> | <math>~x' = \xi_1</math> (radius) |
<math>~\mu'</math> (total mass) |
<math>~\frac{\rho_c}{\bar\rho} = \frac{(x')^3}{3\mu'}</math> | |
| Lane (1870) | 3.656 | 2.741 | 5.943 | 5.355 | 2.188 | 23.39 |
| Emden (1907) | 3.6571 | 2.7171 | 6.0004 | 5.4172 | 2.2010 | 24.08 |
| Horedt (2004) | 3.65375374 | 2.714055 | 5.990705 | 5.35527546 | 2.187200 | 23.40645 |
According to our accompanying summary of structural form factors, the central-to-mean density of an isolated polytropic configuration is,
|
<math>~\frac{\rho_c}{\bar\rho} = \frac{1}{\mathfrak{f}_M}</math> |
<math>~=</math> |
<math>~\biggl[- \frac{3}{\xi} \frac{d\Theta_H}{d\xi}\biggr]^{-1}_{\xi_1}</math> |
<math>~=</math> |
<math>~\frac{(x')^3}{3\mu^'} \, .</math> |
The value of this density ratio, <math>~\rho_c/\bar\rho</math>, as determined for both models from the dimensionless masses and radii calculated by all three researchers has also been included for comparison in this table.
Lane (1870) did not publish a table of numbers to detail how the density varied with radius throughout the interiors of his pair of polytropic models. But both Emden (1907) and Horedt (2004) did. From the tabulated data provided by these two researchers — see below — we have constructed curves showing how the dimensionless density (abscissa),
|
<math>~\frac{\rho}{\bar\rho}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\rho_c}{\bar\rho}\biggr) \Theta_H^n\, ,</math> |
varies with the fractional radius (ordinate), <math>~\xi/\xi_1</math>, in both of Lane's (1870) models. These curves are displayed in the right-hand panel of the accompanying figure: The solid blue curve (and the accompanying small, filled, yellow circular markers) shows the density variation in the model for which <math>k = 1.4 = \tfrac{7}{5} ~\Rightarrow ~n = \tfrac{5}{2}</math> as documented by Emden (and by Horedt); the solid green curve (and the accompanying small, filled, purple circular markers) shows the density variation in the model for which <math>k = 1\tfrac{2}{3} = \tfrac{5}{3} ~\Rightarrow ~n = \tfrac{3}{2}</math> as documented by Emden (and by Horedt).
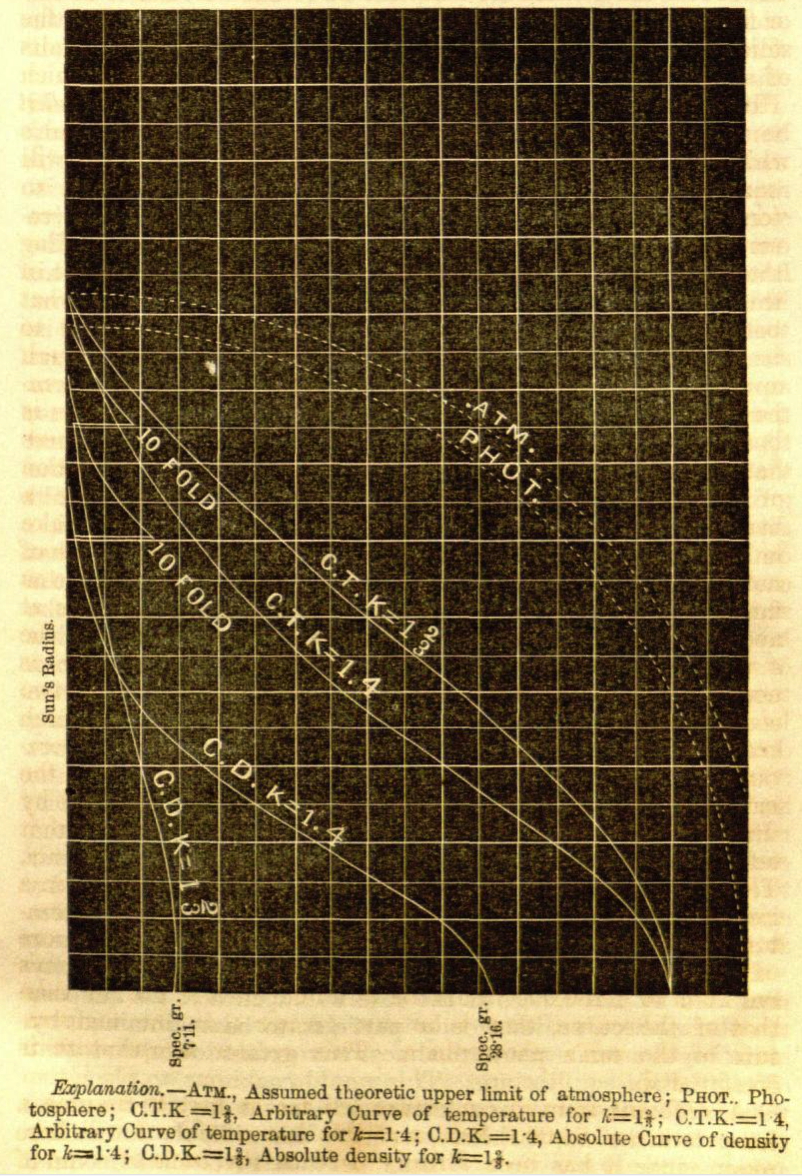 |
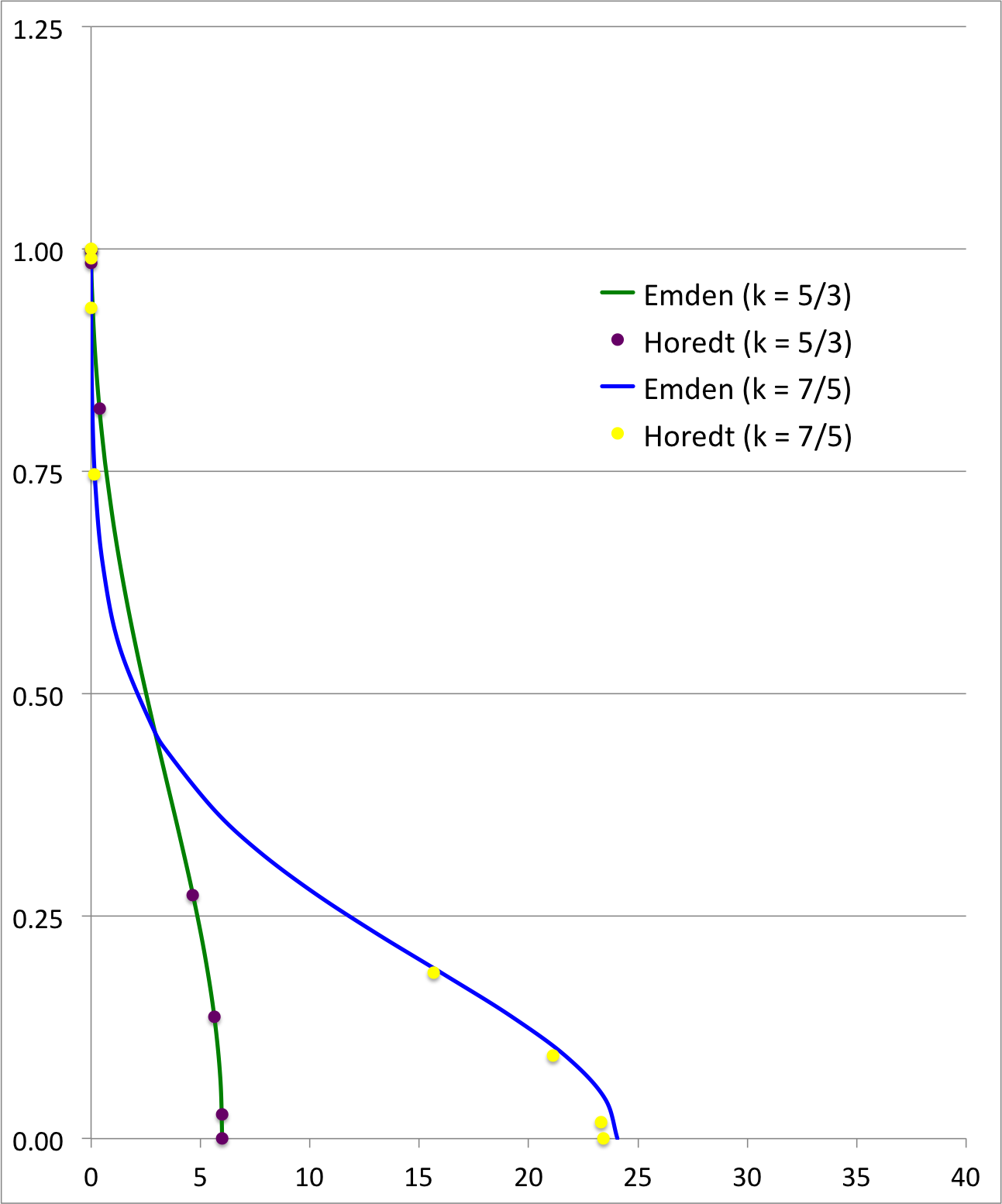 |
The only diagram that appears in Lane's (1870) publication has been reproduced here, in the left-hand panel of our figure. Our pair of plotted curves (right-hand panel of our figure) appear to match the pair of curves that have been drawn in the bottom, left-hand portion of Lane's diagram; the caption accompanying Lane's diagram identifies these curves as plots of the "Absolute density" for <math>~k = 1\tfrac{2}{3}</math> and <math>~k = 1.4</math>. We conclude that, in essentially all respects, Lane's published models provide quantitatively accurate representations of spherical polytropes having indexes, <math>~n = \tfrac{3}{2}</math> and <math>~n = \tfrac{5}{2}</math>.
Published n = 3/2 Tabulations
|
|
Published n = 5/2 Tabulations
|
|

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |