User:Tohline/Apps/Ostriker64

From VistrailsWiki
Jump to navigation Jump to search

Polytropic & Isothermal Tori

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Overview

Here we will focus on the analysis of the structure self-gravitating tori that are composed of compressible — specifically, polytropic and isothermal — fluids as presented in a series of papers by Jeremiah P. Ostriker:

I believe that much, if not all, of this material was drawn from Ostriker's doctoral dissertation research at the University of Chicago (and Yerkes Observatory) under the guidance of S. Chandrasekhar.


Coordinate System

In §IIa of Paper II, Ostriker defines a set of orthogonal coordinates, <math>~(r,\phi,\theta)</math>, that is related to the traditional Cartesian coordinate system, <math>~(x,y,z)</math>, via the relations,

<math>~x</math>

<math>~=</math>

<math>~(R+r\cos\phi)\cos\theta \, ,</math>

<math>~y</math>

<math>~=</math>

<math>~(R+r\cos\phi)\sin\theta \, ,</math>

<math>~z</math>

<math>~=</math>

<math>~r\sin\phi \, .</math>

As Ostriker states, "The coordinate <math>~r</math> is the distance from a reference circle of radius <math>~R</math> (later chosen to be the major radius of the ring) …" The angle, <math>~\theta</math>, plays the role of the azimuthal angle, as is familiar in both cylindrical and spherical coordinates, while, here, <math>~\phi</math> is a meridional-plane polar angle measured counterclockwise from the equatorial plane. For axisymmetric systems, there will be no dependence on the azimuthal angle, so the pair of relevant coordinates in the meridional plane are,

<math>~\varpi \equiv (x^2+y^2)^{1 / 2}</math>

<math>~=</math>

<math>~R+r\cos\phi \, ,</math>

    and,    

<math>~z</math>

<math>~=</math>

<math>~r\sin\phi \, .</math>

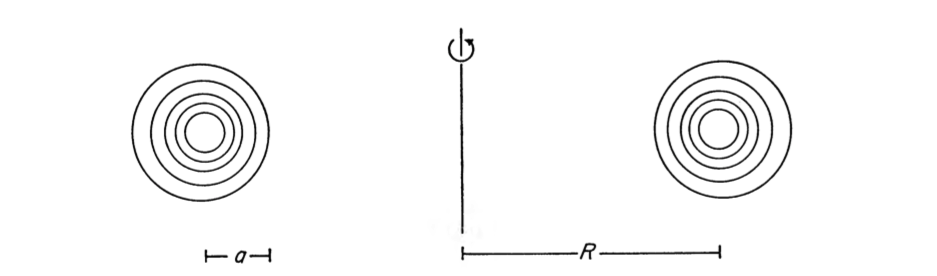
Figure 1 extracted without modification from p. 1077 of J. P. Ostriker (1964; Paper II)

"The Equilibrium of Self-Gravitating Rings"

ApJ, vol. 140, pp. 1067-1087 © American Astronomical Society

Figure 1 from Ostriker (1964) Paper II

Based on my (initial, casual) study of this paper, Figure 1 appears to illustrate a configuration in which the density is constant on various nested toroidal surfaces such that, working from the highest density location, outward, the location <math>~R</math> of the center of each torus shifts to larger and larger values. It would therefore appear as though Ostriker's <math>~R</math> must be a function of the density-marker. Using the subscript, <math>~i</math>, as the marker, we represent the density as a function, <math>~\rho(r_i)</math>, and recognize that <math>~R = R(r_i)</math> as well.

We recognize that the radial coordinate, <math>~\eta</math>, in a toroidal-coordinate system behaves in this same manner. Each <math>~\eta = ~ \mathrm{const}</math> surface is a circle of radius, <math>~d</math>, whose center is located a distance from the symmetry axis, <math>~R_0 = \sqrt{a^2 + d^2}</math>. And, holding <math>~a</math> fixed, the accompanying definition is,

<math>~\cosh\eta = \frac{d}{R_0} =\biggl[ 1 + \frac{a^2}{d^2} \biggr]^{-1 / 2} \, .</math>

Comparing this notation with a toroidal coordinate system whose anchor ring is at the meridional-plane location <math>~(\varpi,z) = (a,0)</math>, we find that,

<math>~R+r\cos\phi</math>

<math>~=</math>

<math>~\frac{a\sinh\eta}{(\cosh\eta - \cos\theta)} \, ,</math>      and,

<math>~r\sin\phi</math>

<math>~=</math>

<math>~\frac{a\sin\theta}{(\cosh\eta - \cos\theta)} \, .</math>

It appears that we can make the following direct associations:   <math>~R_0 \leftrightarrow R_\mathrm{JPO}</math> and <math>~d \leftrightarrow r_\mathrm{JPO}</math>. Hence, we have,

<math>~\frac{d\sin\phi}{R_0+d\cos\phi}</math>

<math>~=</math>

<math>~\frac{\sin\theta}{\sinh\eta}</math>

<math>~\Rightarrow ~~~\sin\theta</math>

<math>~=</math>

<math>~\frac{d \sinh\eta \sin\phi}{R_0+d\cos\phi} \, .</math>

And,

<math>~R_0+d\cos\phi</math>

<math>~=</math>

<math>~\frac{a\sinh\eta}{(\cosh\eta - \cos\theta)} </math>

<math>~\Rightarrow ~~~\cos\theta</math>

<math>~=</math>

<math>~\cosh\eta - \frac{a\sinh\eta}{R_0+d\cos\phi} \, .</math>

Putting these together we find that,

<math>~1 = \sin^2\theta + \cos^2\theta</math>

<math>~=</math>

<math>~ \biggl[\frac{d \sinh\eta \sin\phi}{R_0+d\cos\phi} \biggr]^2 + \biggl[ \cosh\eta - \frac{a\sinh\eta}{R_0+d\cos\phi} \biggr]^2 </math>

<math>~\Rightarrow ~~~ (R_0 + d\cos\phi)^2</math>

<math>~=</math>

<math>~ [d \sinh\eta \sin\phi]^2 + [ \cosh\eta(R_0 + d\cos\phi) - a\sinh\eta]^2 </math>

See Also

The following quotes have been taken from Petroff & Horatschek (2008):

§1:   "The problem of the self-gravitating ring captured the interest of such renowned scientists as Kowalewsky (1885), Poincaré (1885a,b,c) and Dyson (1892, 1893). Each of them tackled the problem of an axially symmetric, homogeneous ring in equilibrium by expanding it about the thin ring limit. In particular, Dyson provided a solution to fourth order in the parameter <math>~\sigma = a/b</math>, where <math>~a = r_t</math> provides a measure for the radius of the cross-section of the ring and <math>~b = \varpi_t</math> the distance of the cross-section's centre of mass from the axis of rotation."

§7:   "In their work on homogeneous rings, Poincaré and Kowalewsky, whose results disagreed to first order, both had made mistakes as Dyson has shown. His result to fourth order is also erroneous as we point out in Appendix B."

  1. Shortly after their equation (3.2), Marcus, Press & Teukolsky make the following statement: "… we know that an equilibrium incompressible configuration must rotate uniformly on cylinders (the famous "Poincaré-Wavre" theorem, cf. Tassoul 1977, &Sect;4.3) …"


 

Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/Apps/Ostriker64&oldid=16180"