CGH: Appertures that are Parallel to the Image Screen

This chapter is intended primarily to replicate §I.A from the online class notes — see also an associated Preface and the original Table of Contents — that I developed in conjunction with a course that I taught in 1999 on the topic of Computer Generated Holography (CGH) for a subset of LSU physics majors who were interested in computational science.

Propagation of Light

Here we reference heavily the traveling, wave-like nature of light and, as is customary, use <math>~c</math> to represent its speed of propagation through space. Consider a single ray of light of wavelength, <math>~\lambda</math>, that is traveling in the <math>~x</math>-direction. Its amplitude, <math>~a</math>, will vary with time in a sinusoidal fashion as described by the equation,

<math>~a(x) = a_0\cos\biggl(\frac{2\pi x}{\lambda} + \phi_0 \biggr) \, ,</math>

where: the light-wave's peak-to-peak brightness is <math>~2a_0</math>; <math>~\phi_0</math> is the "phase" that the oscillatory wave displays at a reference location, <math>~x=0</math>, when the reference time, <math>~t = 0</math>; and <math>~x = ct</math>. As is demonstrated, for example, in our accompanying discussion of various, equivalent, Fourier series expressions, this equation can be rewritten in the form,

<math>~a(x) = a_0 e^{2\pi x/\lambda + \phi_0} \, .</math>

One-Dimensional Aperture

General Concept

Figure 1

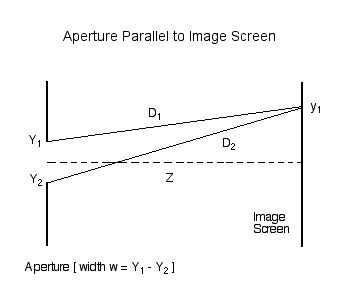
Consider the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w</math>. First, as illustrated in Figure 1, consider the contribution due only to two rays of light: one coming from location <math>~Y_1</math> at the top edge of the slit (a distance <math>~D_1</math> from point <math>~y_1</math> on the screen) and another coming from location <math>~Y_2</math> at the bottom edge of the slit (a distance <math>~D_2</math> from the same point on the screen).

The complex number, <math>~A</math>, representing the light amplitude and phase at <math>~y_1</math> will be,

<math>~ a(Y_1) e^{i(2\pi D_1/\lambda + \phi_1)} + a(Y_2) e^{i(2\pi D_2/\lambda + \phi_2)} \, , </math>

where, <math>~\lambda</math> is the wavelength of the light, <math>~a(Y_j)</math> is the brightness of the light at point <math>~Y_j</math> on the aperture, and <math>~\phi_j</math> is the phase of the light as it leaves point <math>~Y_j</math>.

Now, if we consider for the moment that at all locations on the aperture, <math>~Y_j</math>, the light has a brightness <math>~a(Y_j) = 1</math> and a phase <math>~\phi_j = 0</math>, then,

<math>~A_0 \biggl[1 + e^{i(2\pi/\lambda)(D_2 - D_1)} \biggr] \, ,</math>

where, <math>~A_0 = e^{i(2\pi D_1/\lambda)}</math>. So the question of whether the amplitude at <math>~y_1</math> on the image screen will be bright due to constructive interference or faint as a result of destructive interference comes down to a question of what the phase difference is between the two distances <math>~D_1</math> and <math>~D_1</math> where,

<math>~D_j</math>	<math>~\equiv</math>	<math>~ [(Y_j - y_1)^2 + Z^2 ]^{1 / 2} </math>
	<math>~=</math>	<math>~ [Z^2 + y_1^2 - 2y_1 Y_j + Y_j^2 ]^{1 / 2} </math>
	<math>~=</math>	<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} + \frac{Y_j^2}{L^2} \biggr]^{1 / 2} </math>

and,

<math>~\equiv</math>

Utility of FFT Techniques

Let's rewrite the first of our above equations in a form that takes into account many more than just two points along the aperture. That is,

<math>~A(y_1)</math>	<math>~=</math>	<math>~\sum_j a_j e^{i(2\pi D_j/\lambda + \phi_j)} \, , </math>
	<math>~=</math>	<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) \biggr] \, . </math>

Note that this is identical to the expression,

<math>~\sum_j a_j \biggl[\cos\phi_j + i \sin\phi_j \biggr] \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda}\biggr) \biggr] \, . </math>

In the more restrictive case when we assume that everywhere along the aperture the phase <math>~\phi_j = 0</math>, we have,

<math>~A(y_1)</math>	<math>~=</math>	<math>~\sum_j a_j e^{i(2\pi D_j/\lambda)} \, , </math>
	<math>~=</math>	<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} \biggr) \biggr] \, , </math>

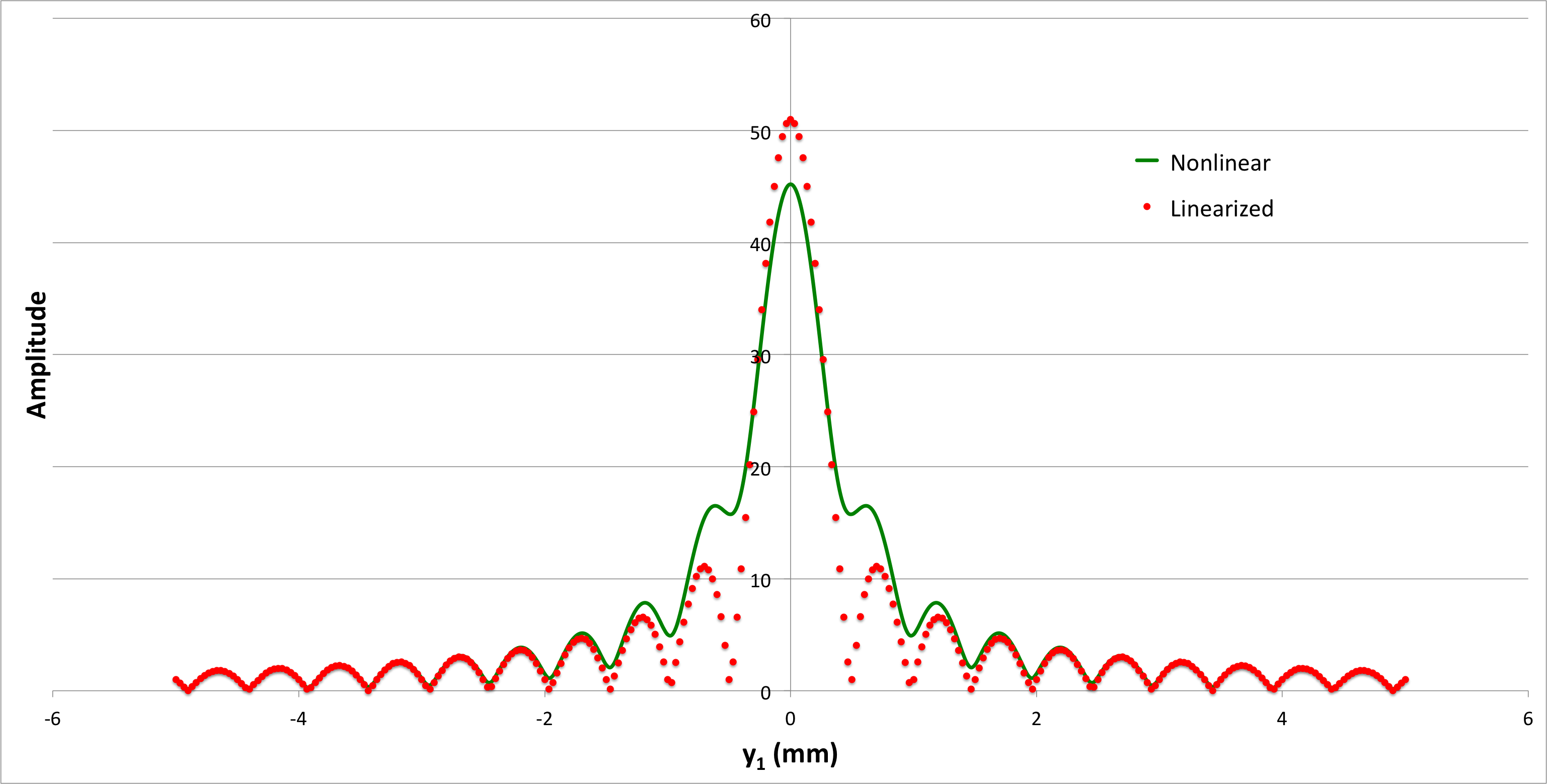
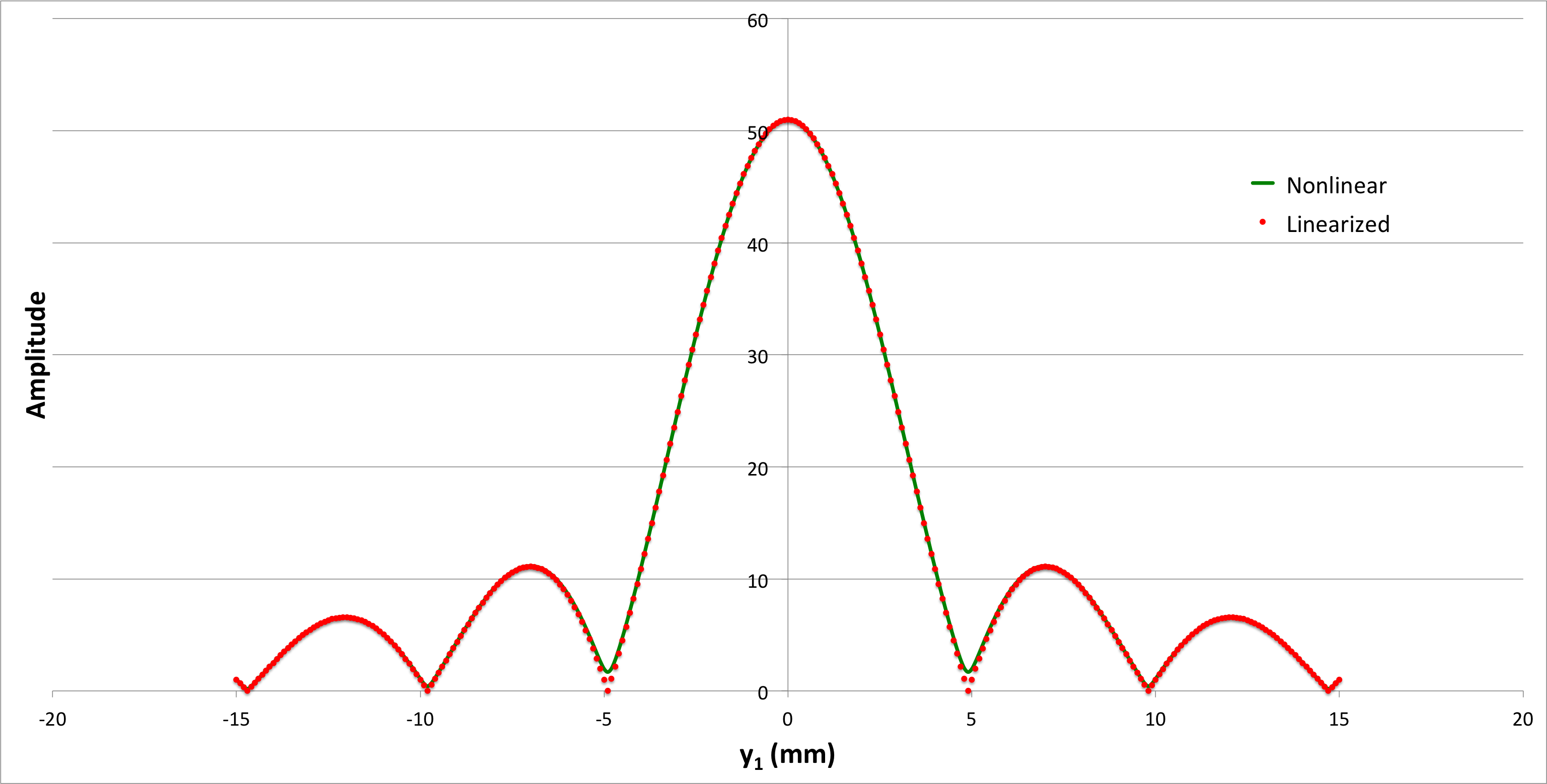
where, in each of these expressions, we have replaced <math>~a(Y_j)</math> with <math>~a_j</math>. After acknowledging that the function, <math>~A(y_1)</math>, is complex — with <math>~\mathcal{R}e(A)</math> being given by the sum over cosine terms and <math>~\mathcal{I}m(A)</math> being given by the sum over sine terms — it is clear that the brightness of each point on the image screen is given by (the square root of) <math>~A</math> multiplied by its complex conjugate, <math>~A^*</math>, that is, by the expression, <math>~ (A\cdot A^*)^{1 / 2}</math>. Figures 1 & 2 show how this brightness (amplitude) varies across the image screen for the case of a monochromatic light of wavelength, <math>~\lambda = 500</math> nanometers, impinging on a single slit that is 1 mm in width; for all curves, the amplitude has been determined by summing over <math>~j_\mathrm{max} = 51</math> equally spaced points across the slit. The results displayed in Figure 1 are for an image screen that is placed <math>~Z = 1</math> meter from the slit, while Figure 2 displays results for an image screen that is placed a distance, <math>~Z = 10</math> m from the slit.

Figure 1: <math>~w = 1~\mathrm{mm}; Z = 1~\mathrm{m}; \lambda = 500~\mathrm{nm}; j_\mathrm{max} = 51</math>
$First Plot of Single-Slit Diffraction Pattern$

Two curves appear in both Figure 1 and Figure 2. The solid green curve was obtained by plugging the precise, "nonlinear" determination of <math>~D_j</math> — that is, the mathematical expression for <math>~D_j</math>, as given above — into the arguments of the trigonometric functions, while the dotted red curve was obtained by using the approximate, "linearized" expression for <math>~D_j</math>, as will now be described.

Figure 2: <math>~w = 1~\mathrm{mm}; Z = 10~\mathrm{m}; \lambda = 500~\mathrm{nm}; j_\mathrm{max} = 51</math>
$Second Plot of Single-Slit Diffraction Pattern$

If we assume that, for all <math>~j</math>,

<math>~\biggl| \frac{Y_j}{L}\biggr| \ll 1</math>

— in the present context, this generally will be equivalent to assuming that the width of the aperture is much much less than the distance <math>~(Z)</math> separating the aperture from the image screen — we can drop the quadratic term in favor of the linear one in the above expression for <math>~D_j</math> and deduce that,

<math>~D_j</math>	<math>~\approx</math>	<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} \biggr]^{1 / 2} </math>
	<math>~\approx</math>	<math>~ L \biggl[1 - \frac{y_1 Y_j}{L^2} \biggr] \, . </math>

Hence, we have,

<math>~A(y_1)</math>	<math>~=</math>	<math>~A_0 \sum_j a_j e^{-i[2\pi y_1 Y_j/(\lambda L)]} \, , </math>
	<math>~=</math>	<math>~A_0 \sum_j a_j \biggl[ \cos\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) - i \sin\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) \biggr] \, , </math>

where, now, <math>~A_0 = e^{i2\pi L/\lambda}</math>.

Notice that this expression matches what we have referred to elsewhere as the Complex Fourier Series Expression. When written in this form, it should immediately be apparent why discrete Fourier transform techniques (specifically FFT techniques) are useful tools for evaluation of the complex amplitude, <math>~A</math>. See further elaboration below.

Location of the Dark Fringe(s)

As has been described in multiple online references, the locations across the image screen where complete destructive interference occurs can be determined straightforwardly using geometric relationships. For example, in terms of the angle, <math>~\theta</math>, defined such that,

<math>~\tan\theta = \frac{y_1}{Z} \, ,</math>

the distance from the central brightness peak to the first location where the brightness/amplitude goes to zero — i.e., the location of the first dark fringe — is given by the relation,

<math>~\sin\theta = \frac{\lambda}{w} \, .</math>

(For each successive fringe, labeled by the positive integer, <math>~m</math>, the relation is, <math>~\sin\theta_m = m\lambda/w.</math>) Hence, acknowledging that usually <math>~\lambda/w \ll 1</math>, we find that,

<math>~y_1\biggr\|_{1^\mathrm{st} \mathrm{fringe}}</math>	<math>~=</math>	<math>~Z \tan\theta = Z \sin\theta [ 1 - \sin^2\theta ]^{-1 / 2}</math>
	<math>~=</math>	<math>~\frac{\lambda Z}{w} \biggl[ 1 - \biggl(\frac{\lambda }{w}\biggr)^2 \biggr]^{-1 / 2}</math>
	<math>~\approx</math>	<math>~\frac{\lambda Z}{w} \, .</math>

In the context of Figure 2, this means that, <math>~y_1|_{1^\mathrm{st} \mathrm{fringe}} = 5</math> millimeters, while, in Figure 1, <math>~y_1|_{1^\mathrm{st} \mathrm{fringe}} = 0.5</math> millimeters — in both cases, this is in agreement with the plotted linearized amplitude curves.

Parallels With Standard Fourier Series

Let's draw parallels between the above discussion of the single-slit diffraction pattern and our separate presentation of the standard treatment of Fourier Transforms.

Standard Fourier Transform Treatment

Single-Slit (Linearized) Diffraction
Replace <math>~L</math> with <math>~\mathcal{D}</math>

<math>~a_m</math>	<math>~=</math>	<math>~ \frac{2}{L_\mathrm{max}} \cdot \sum_{L=1}^{L_\mathrm{max}} \rho(\theta_L) \cos\biggl[m \biggl(\frac{2\pi L}{L_\mathrm{max}}\biggr)\biggr] \, , </math>
<math>~b_m</math>	<math>~=</math>	<math>~ \frac{2}{L_\mathrm{max}} \cdot \sum_{L=1}^{L_\mathrm{max}} \rho(\theta_L) \sin\biggl[m \biggl(\frac{2\pi L}{L_\mathrm{max}}\biggr)\biggr] \, . </math>

It is sometimes useful to view <math>~a_m</math> and <math>~b_m</math> as, respectively, the real and imaginary components of a complex variable; for example,

in which case,

Amplitude	<math>~=</math>	<math>~[a_m^2 + b_m^2]^{1 / 2} \, ,</math>
Phase	<math>~=</math>	<math>~\tan^{-1}\biggl[\frac{-b_m}{a_m} \biggr]</math>

<math>~A_0 \biggl[ \mathcal{R}e(A) - i ~\mathcal{I}m(A) \biggr] \, , </math>

where,

<math>~\mathcal{R}e[A(n\Delta y_1)]</math>	<math>~=</math>	<math>~\sum_j a_j \cos\biggl[n\Delta y_1 \biggl(\frac{2\pi}{\lambda \mathcal{D}} \biggr)j\Delta Y \biggr] \, , </math>
<math>~\mathcal{I}m[A(n\Delta y_1)]</math>	<math>~=</math>	<math>~ \sum_j a_j \sin\biggl[n\Delta y_1 \biggl(\frac{2\pi}{\lambda \mathcal{D}} \biggr)j\Delta Y \biggr] \, . </math>

A comparison between the two discussions reveals the following variable mappings:

<math>~m</math>	<math>~\leftrightarrow</math>	<math>~n</math>
<math>~L</math>	<math>~\leftrightarrow</math>	<math>~j</math>
<math>~\frac{2\pi}{L_\mathrm{max}}</math>	<math>~\leftrightarrow</math>	<math>~\Delta y_1 \biggl(\frac{2\pi}{\lambda \mathcal{D}} \biggr) \Delta Y </math>
<math>~\rho(\theta_L)</math>	<math>~\leftrightarrow</math>	<math>~a(Y_j)</math>

Drawing from an accompanying discussion, the corresponding complex Fourier series expression is,

<math>~ \frac{1}{2}\sum_{m = -\infty}^{m = + \infty} B(m) e^{i\omega_m x} \, , </math>

where, for <math>~m = 0, \pm 1, \pm 2, \pm 3, \dots~,</math>

<math>~\omega_m</math>

In other words,

<math>~f(x)</math>	<math>~=</math>	<math>~ \frac{1}{2}\biggl[ B(m) e^{i\omega_m x}\biggr]_{m=0} + \frac{1}{2} \sum_{m = 1}^{m = + \infty} \biggl[ B(m) e^{i\omega_m x} + B(-m) e^{-i\omega_m x}\biggr] </math>
	<math>~=</math>	<math>~ \frac{B(0)}{2}\biggl[ \cos(\omega_m x) + i\sin(\omega_mx)\biggr]_{m=0} + \frac{1}{2} \sum_{m = 1}^{m = + \infty} \biggl\{ (a_m - ib_m)\biggl[ \cos(\omega_m x) + i\sin(\omega_mx)\biggr] + (a_m + ib_m) \biggl[ \cos(\omega_m x) - i\sin(\omega_mx)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{B(0)}{2} + \frac{1}{2} \sum_{m = 1}^{m = + \infty} \biggl\{ a_m \biggl[ \cos(\omega_m x) + i\sin(\omega_mx) \biggr] - ib_m \biggl[ \cos(\omega_m x) + i\sin(\omega_mx) \biggr] </math>
		<math>~ + a_m \biggl[ \cos(\omega_m x) - i\sin(\omega_mx)\biggr] + ib_m \biggl[ \cos(\omega_m x) - i\sin(\omega_mx)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{B(0)}{2} + \frac{1}{2} \sum_{m = 1}^{m = + \infty} \biggl\{ a_m \cos(\omega_m x) + i ~a_m \sin(\omega_mx) - i~b_m \cos(\omega_m x) + b_m\sin(\omega_mx) </math>
		<math>~ + a_m \cos(\omega_m x) - i~a_m\sin(\omega_mx) + ib_m \cos(\omega_m x) + b_m\sin(\omega_mx) \biggr\} </math>
	<math>~=</math>	<math>~ \frac{B(0)}{2} + \sum_{m = 1}^{m = + \infty} \biggl\{ a_m \cos(\omega_m x) + b_m\sin(\omega_mx) \biggr\} \, . </math>

Now, carry out the inverse transform.

Standard Fourier Transform Treatment

Single-Slit (Linearized) Diffraction
Replace <math>~L</math> with <math>~\mathcal{D}</math>

<math>~\rho(\theta_L)</math>

<math>~ \frac{a_0}{2} + \sum_{m=1}^{L_\mathrm{max}/2} \biggl\{ a_m \cos\biggl[m \biggl(\frac{2\pi L}{L_\mathrm{max}}\biggr)\biggr] + b_m\sin\biggl[m \biggl(\frac{2\pi L}{L_\mathrm{max}}\biggr)\biggr] \biggr\} </math>

<math>~ \frac{\mathcal{R}e(A_{n=0})}{2} + A_0 \sum_{n=1}^{n_\mathrm{max}/2} \biggl\{ \mathcal{R}e(A_n) \cos\biggl[n \biggl(\frac{2\pi j}{\lambda \mathcal{D}} \biggr)\Delta y_1 \Delta Y \biggr] + \mathcal{I}m(A_n)\sin\biggl[n\biggl(\frac{2\pi j}{\lambda \mathcal{D}} \biggr)\Delta y_1 \Delta Y \biggr] \biggr\} </math>

Parallels With Example #2

This "one dimensional aperture" analysis should exhibit features that strongly resemble the features that appear in our accompanying discussion of the Fourier series associated with a "square wave". In both cases — after performing both a Fourier transform and the inverse transform — the ultimate series expression that will represent the (square wave) amplitude across the aperture will take the form,

<math>~ \frac{a_0}{2} + \sum_{n=1}^{\infty} \biggl[ a_n\cos \biggl(\frac{n\pi x}{L}\biggr) + b_n\sin \biggl(\frac{n\pi x}{L}\biggr) \biggr] \, . </math>

This function clearly repeats itself at spatial intervals of <math>~x \pm 2L</math>. Hence, we must acknowledge that, even if the initial state is intended to represent a single aperture, the inverse transform will produce an infinite set of identical apertures that are spaced (center-to-center) at intervals of <math>~2L</math>. We can presumably arrange to have successive apertures of width, <math>~2c</math>, widely spaced from one another by picking a value of <math>~|c/L | \ll 1</math>.

In the "square wave" analysis in which the brightness across the aperture is specified by a continuous function, the amplitude, <math>~a_n</math>, of each Fourier mode, <math>~n</math>, is given by the expression,

<math>~ \frac{1}{L} \int_{-c}^{c} \cos\biggl( \frac{n\pi x}{L} \biggr) dx = \biggl(\frac{2c}{L} \biggr) \mathrm{sinc}(\alpha_n)\, , </math>

where, <math>~\alpha_n \equiv n\pi c/L</math>. On the other hand, when a discrete Fourier transform is used, the analogous Fourier amplitude is given by the expression,

<math>~\mathcal{R}e[A(n\Delta y_1)]</math>

<math>~\sum_{j=-j_\mathrm{max}}^{j_\mathrm{max}} \cos\biggl[n\Delta y_1 \biggl(\frac{2\pi}{\lambda \mathcal{D}} \biggr)\frac{j c}{j_\mathrm{max}} \biggr] \, . </math>

Comparing the two expressions, we recognize first that the integer, <math>~n</math>, has the same meaning in both; and, second, that <math>~x \leftrightarrow jc/j_\mathrm{max}</math>. Therefore — after recognizing that <math>~\mathcal{D} \approx Z</math> — it must also be true that,

<math>~\frac{1}{L} \leftrightarrow \frac{2\Delta y_1}{\lambda \mathcal{D}} \approx \frac{2\Delta y_1}{\lambda Z} \, .</math>

Next we notice, from the "square wave" analysis, that since the amplitude of the the diffraction pattern, <math>~a_n</math>, varies as <math>~\mathrm{sinc}(\alpha_n)</math>, the first dark fringe will arise when <math>~\alpha_n = \pi</math>, that is, when <math>~n = n_\pi \equiv L/c</math>. But, as explained above, from geometric arguments associated with the "one dimensional aperture" analysis, we expect the first dark fringe on the image screen to arise when,

<math>~\frac{y_1}{Z}</math>	<math>~=</math>	<math>~\frac{\lambda}{2c} </math>
<math>~\Rightarrow ~~~\frac{2}{\lambda Z}</math>	<math>~=</math>	<math>~\frac{1}{y_1 c} </math>
<math>~\Rightarrow ~~~\frac{\Delta y_1}{y_1 c} </math>	<math>~=</math>	<math>~\frac{2\Delta y_1}{\lambda Z} ~~\rightarrow ~~ \frac{1}{L} </math>
<math>~\Rightarrow ~~~n</math>	<math>~=</math>	<math>~ \frac{L}{c} ~~~\Rightarrow~~ n = n_\pi \, ,</math>

where this last relation has been derived by recognizing that, quite generally by design, <math>~y_1 = n\Delta y_1</math>. So, these two separate ways of identifying the location of the first dark fringe agree with one another.

COMMENT: Throughout our discussion of computer-generated holography, we will find it necessary to construct a discretized image screen and, hence, will need to discuss the corresponding discretized modal amplitude ("sinc") function. This discretized amplitude function can be treated as a multiple-slit source function and, via an inverse Fourier transform, be used to regenerate the original square-wave (or analogous) function. This square wave of width, <math>~2c</math>, will necessarily be accompanied by multiple duplicate images that are spaced a (center-to-center) distance, <math>~2L</math>, apart. The result that we have just derived tells us that the relative spacing of these duplicate images will be large, relative to the width of the original square wave, if the discretization of the image screen is done in such a way as to ensure that <math>~n_\pi</math> is a large number.

Multiple One-Dimensional Apertures

Okay. Let's piece together an image that is generated by a set of <math>~N</math>, identical one-dimensional apertures; each one is uniformly illuminated, but adjacent apertures will, in general, have different illuminations, <math>~\beta_m</math>. Each aperture has width, <math>~2c</math>; and each is separated from its two neighboring apertures by a distance, <math>~2\nu</math>.

Starting with just a pair of slits, and setting the y-direction zero point exactly midway between the two, we can expand upon the accompanying Example #2 discussion to obtain,

<math>~a_n</math>	<math>~=</math>	<math>~ \frac{1}{L} \biggl\{ \int_{\nu}^{\nu +2c} \beta_{+1} \cos\biggl( \frac{n\pi x}{L} \biggr) dx + \int^{-\nu}_{-(\nu +2c)} \beta_{-1}\cos\biggl( \frac{n\pi x}{L} \biggr) dx \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{n\pi} \biggl\{ \int_{n\pi \nu/L}^{n\pi(\nu +2c)/L} \beta_{+1} \cos\theta ~d\theta + \int^{-n\pi \nu/L}_{-n\pi(\nu +2c)/L} \beta_{-1}\cos\theta ~d\theta \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{n\pi} \biggl\{\beta_{+1} \biggl[ \sin\theta \biggr]_{n\pi \nu/L}^{n\pi(\nu +2c)/L} + \beta_{-1}\biggl[ \sin\theta \biggr]^{-n\pi \nu/L}_{-n\pi(\nu +2c)/L} \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{n\pi} \biggl\{\beta_{+1} \biggl[ \sin\biggl( \frac{n\pi \nu }{L} + \frac{2n\pi c}{L}\biggr) - \sin\biggl( \frac{n\pi \nu}{L} \biggr) \biggr] + \beta_{-1}\biggl[\sin\biggl( -~\frac{n\pi \nu}{L} \biggr) - \sin\biggl( -~ \frac{n\pi \nu }{L} - \frac{2n\pi c}{L}\biggr) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{\beta_{+1} + \beta_{-1}}{n\pi} \biggl[ \sin\biggl( \frac{n\pi \nu }{L} + \frac{2n\pi c}{L}\biggr) - \sin\biggl( \frac{n\pi \nu}{L} \biggr) \biggr] \, ; </math>
<math>~b_n</math>	<math>~=</math>	<math>~ \frac{1}{n\pi} \biggl\{ \int_{n\pi \nu/L}^{n\pi(\nu +2c)/L} \beta_{+1} \sin\theta ~d\theta + \int^{-n\pi \nu/L}_{-n\pi(\nu +2c)/L} \beta_{-1}\sin\theta ~d\theta \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{n\pi} \biggl\{ - \beta_{+1} \biggl[ \cos\theta\biggr]_{n\pi \nu/L}^{n\pi(\nu +2c)/L} - \beta_{-1} \biggl[ \cos\theta \biggr]^{-n\pi \nu/L}_{-n\pi(\nu +2c)/L} \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{n\pi} \biggl\{ - \beta_{+1} \biggl[ \cos\biggl( \frac{n\pi \nu}{L} + \frac{2n\pi c}{L} \biggr) - \cos\biggl( \frac{n\pi\nu}{L} \biggr)\biggr] - \beta_{-1} \biggl[ \cos\biggl( - \frac{n\pi\nu}{L} \biggr) - \cos\biggl( -~\frac{n\pi\nu}{L} - ~\frac{2n\pi c}{L} \biggr) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~-~ \frac{1}{n\pi} \biggl\{ \beta_{+1} \biggl[ \cos\biggl( \frac{n\pi \nu}{L} + \frac{2n\pi c}{L} \biggr) - \cos\biggl( \frac{n\pi\nu}{L} \biggr)\biggr] - \beta_{-1} \biggl[ \cos\biggl( \frac{n\pi\nu}{L} + \frac{2n\pi c}{L} \biggr) - \cos\biggl( \frac{n\pi\nu}{L} \biggr) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{\beta_{-1} - \beta_{+1}}{n\pi} \biggl[ \cos\biggl( \frac{n\pi \nu}{L} + \frac{2n\pi c}{L} \biggr) - \cos\biggl( \frac{n\pi\nu}{L} \biggr)\biggr] \, . </math>

Considering, first, the case where the two slits are illuminated equally <math>(~\beta_- = \beta_+)</math>, we see that <math>~b_n = 0</math>, so the amplitude is,

<math>~\|a_n\|</math>	<math>~=</math>	<math>~ \frac{2}{n\pi} \biggl\| \sin\biggl( \frac{n\pi \nu }{L} + \frac{2n\pi c}{L}\biggr) - \sin\biggl( \frac{n\pi \nu}{L} \biggr) \biggr\| </math>
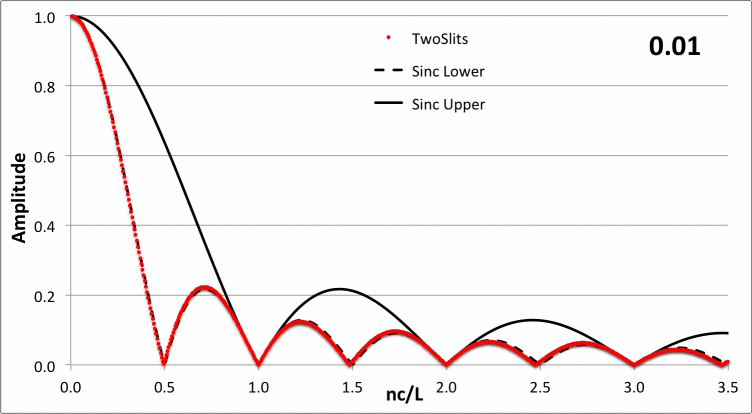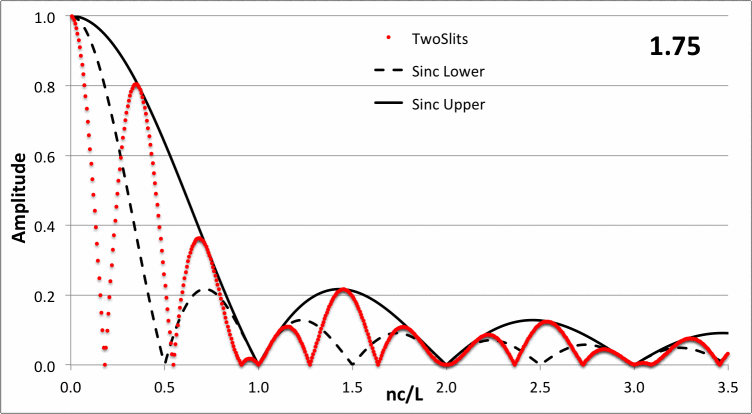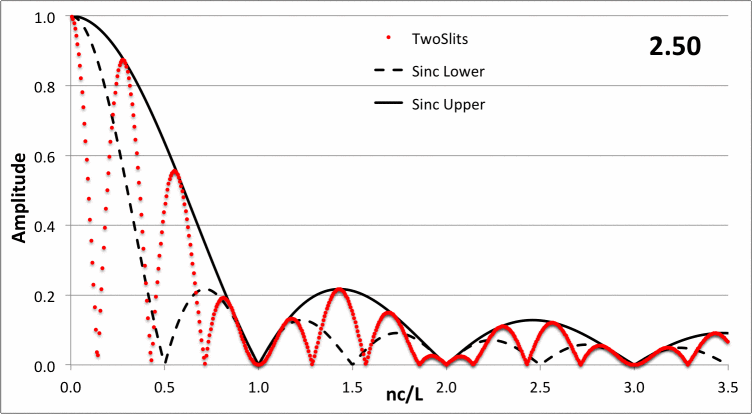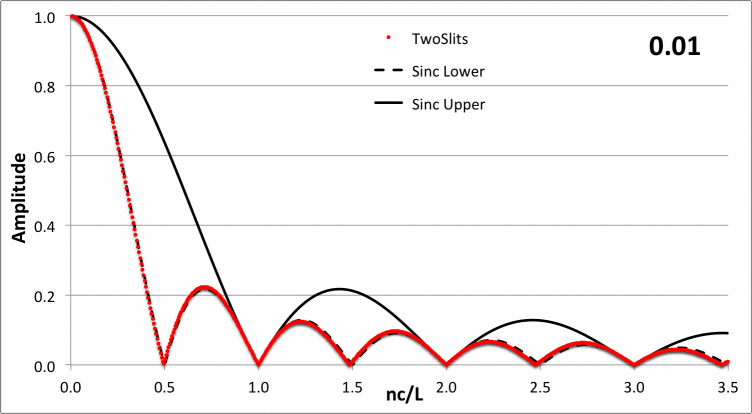
	<math>~=</math>	<math>~ \frac{2c}{L\chi} \biggl\| \sin\biggl( \frac{\chi\nu }{c} + 2\chi \biggr) - \sin\biggl( \frac{\chi\nu}{c} \biggr) \biggr\| \, , </math>

where,

<math>~\chi \equiv \frac{n\pi c}{L} \, .</math>

In the following animated figure, the red-dotted curve shows how <math>~|a_n|</math> varies with <math>~\chi/\pi</math> for a variety of different values of the dimensionless parameter, <math>~0.1 \le \nu/c \le 5</math>, as recorded in the upper-right-hand corner of the plot.

$Diffraction pattern for two-slit aperture$

User:Tohline/Appendix/CGH/ParallelApertures

Contents