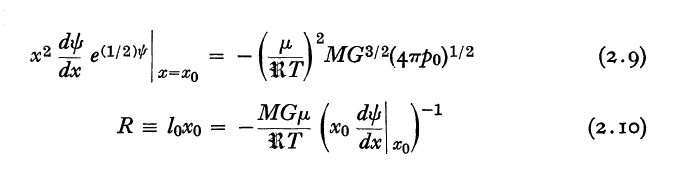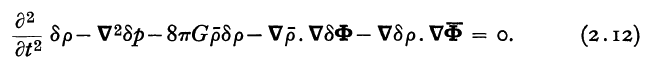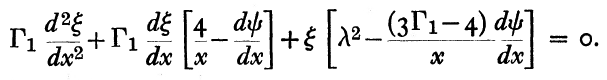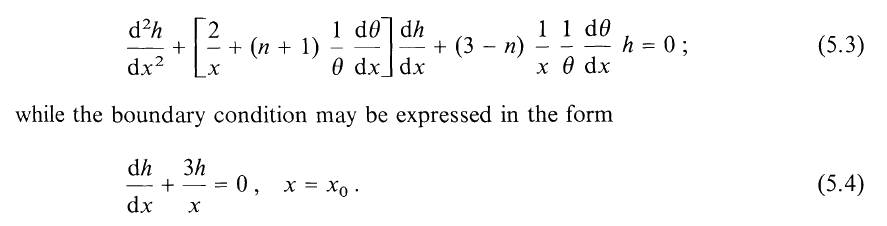Radial Oscillations of Pressure-Truncated Isothermal Spheres

Here we draw primarily from the following three sources:

§5.3.8 (p. 372) of Horedt's (2004) treatise on Polytropes: Applications in Astrophysics and Related Fields
S. Yabushita (1968, MNRAS, 140, 109) — Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres
L. G. Taff & H. M. Horn (1974, MNRAS, 168, 427-432) — Radial Pulsations of Finite Isothermal Gas Spheres

Groundwork

Equilibrium Model

In an accompanying discussion, while reviewing the original derivations of Ebert (1955) and Bonnor (1956), we have detailed the equilibrium properties of pressure-truncated isothermal spheres. These properties have been expressed in terms of the isothermal Lane-Emden function, <math>~\psi(\xi)</math>, which provides a solution to the governing,

Isothermal Lane-Emden Equation

<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>

A parallel presentation of these details can be found in §2 — specifically, equations (2.4) through (2.10) — of Yabushita (1968). Each of Yabushita's key mathematical expressions can be mapped to ours via the variable substitutions presented here in Table 1.

Table 1: Mapping from Yabushita's (1968) Notation to Ours
Yabushita's (1968) Notation:	<math>~x</math>	<math>~\psi</math>	<math>~\mu</math>	<math>~M</math>	<math>~x_0</math>	<math>~p_0</math>
Our Notation:	<math>~\xi</math>	<math>~-\psi</math>	<math>~\bar\mu</math>	<math>~M_{\xi_e}</math>	<math>~\xi_e</math>	<math>~P_e</math>

For example, given the system's sound speed, <math>~c_s</math>, and total mass, <math>~M_{\xi_e}</math>, the expression from our presentation that shows how the bounding external pressure, <math>~P_e</math>, depends on the dimensionless Lane-Emden function, <math>~\psi</math>, is,

<math>~P_e</math>	<math>~=</math>	<math>~\biggl( \frac{c_s^8}{4\pi G^3 M_{\xi_e}^2} \biggr) ~\xi_e^4 \biggl(\frac{d\psi}{d\xi}\biggr)^2_e e^{-\psi_e}</math>
<math>~\Rightarrow ~~~ \xi_e^2 \biggl(\frac{d\psi}{d\xi}\biggr)_e e^{-(1/2)\psi_e}</math>	<math>~=</math>	<math>~\frac{1}{c_s^4}\biggl[ G^3 M_{\xi_e}^2 ~(4\pi P_e)\biggr]^{1 / 2} \, ,</math>

which — see the boxed-in excerpt that follows — exactly matches Yabushita's (1968) equation (2.9), after recalling that the system's sound speed is related to its temperature via the relation,

And, our expression for the truncated configuration's equilibrium radius is,

<math>~\frac{GM_{\xi_e}}{c_s^2} \biggl[ \xi \biggl(\frac{d\psi}{d\xi}\biggr) \biggr]_e^{-1}</math>

which — see the boxed-in excerpt that follows — matches Yabushita's (1968) equation (2.10).

Equations extracted^† from p. 110 of S. Yabushita (1968, MNRAS, 140, 109)

"Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres"

MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society

^†Mathematical expressions displayed here with layout modified from the original publication.

Also, as has been summarized in our accompanying discussion of the equilibrium properties of pressure-truncated isothermal spheres, we have,

<math>~r_0 </math>	<math>~=</math>	<math>~\biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi \, ;</math>
<math>~P_0 = c_s^2 \rho_0 </math>	<math>~=</math>	<math>~(c_s^2 \rho_c) e^{-\psi} \, ;</math>
<math>~M_r </math>	<math>~=</math>	<math>~\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ \xi^2 \frac{d\psi}{d\xi} \biggr] \, .</math>

Hence, for isothermal configurations,

<math>~g_0 \equiv \frac{GM_r}{r_0^2}</math>	<math>~=</math>	<math>~G\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ \xi^2 \frac{d\psi}{d\xi} \biggr] \biggl[ \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi\biggr]^{-2}</math>
	<math>~=</math>	<math>~c_s^2 \biggl( \frac{4\pi G \rho_c}{c_s^2} \biggr)^{1 / 2} \biggl( \frac{d\psi}{d\xi} \biggr) \, . </math>

Linearized Wave Equation

In our introductory discussion of techniques that facilitate linear stability analyses, we derived what we now repeatedly refer to as the "key" form of the

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

Here we review two published articles that have presented a partial analysis of radial modes of oscillation in pressure-truncated isothermal spheres. The analyses presented in both of these papers, effectively, employ this key wave equation, but the authors of these articles present it in different forms.

Yabushita (1968)

The linearized wave equation that Yabushita (1968) used to examine the radial pulsation modes of pressure-truncated isothermal spheres is displayed in the following, boxed-in image:

Equation extracted from p. 111 of S. Yabushita (1968, MNRAS, 140, 109)

"Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres"

MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society

This equation can be obtained straightforwardly through a strategic combination of three of the following four linearized principal governing equations that we have derived in our accompanying, broad introductory discussion of linear stability analyses, namely,

Linearized
Equation of Continuity
<math> \frac{\partial \rho_1}{\partial t} + \rho_0\nabla\cdot \vec{v} + \vec{v}\cdot \nabla\rho_0 = 0 , </math>

Linearized
Euler Equation
<math> ~\frac{\partial \vec{v}}{\partial t} = - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 \, , </math>

Linearized
Adiabatic Form of the
First Law of Thermodynamics

<math> P_1 = \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1\, , </math>

Linearized
Poisson Equation

<math> \nabla^2 \Phi_1 = 4\pi G \rho_1\, . </math>

Taking the partial time-derivative of the linearized equation of continuity gives,

<math>~- \nabla\cdot \frac{\partial \vec{v}}{\partial t} </math>

<math>~\frac{1}{\rho_0}\frac{\partial^2 \rho_1}{\partial t^2} + \frac{\nabla\rho_0}{\rho_0} \cdot \frac{\partial\vec{v}}{\partial t} \, ;</math>

and, taking the divergence of the linearized Euler equation gives,

<math>~-\nabla\cdot \frac{\partial \vec{v}}{\partial t} </math>

<math>~\nabla^2 \Phi_1 + \nabla\cdot \biggl[\frac{1}{\rho_0} \nabla P_1\biggr] - \nabla \cdot \biggl[ \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] \, .</math>

Combining the two, then making two substitutions using (1) the linearized Poisson equation and (2) the linearized Euler equation, we have,

<math>~\frac{\partial^2 \rho_1}{\partial t^2} + \nabla\rho_0 \cdot \frac{\partial\vec{v}}{\partial t} </math>	<math>~=</math>	<math>~\rho_0 \nabla^2 \Phi_1 + \rho_0 \nabla\cdot \biggl[\frac{1}{\rho_0} \nabla P_1\biggr] - \rho_0\nabla \cdot \biggl[ \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] </math>
<math>~\Rightarrow ~~~ \frac{\partial^2 \rho_1}{\partial t^2} + \nabla\rho_0 \cdot \biggl[ - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] </math>	<math>~=</math>	<math>~4\pi G \rho_0 \rho_1 + \nabla^2 P_1 + \rho_0 \nabla P_1 \cdot \nabla \biggl(\frac{1}{\rho_0} \biggr) - \rho_0\nabla \cdot \biggl[ \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] \, .</math>

Rearranging terms, and using the replacement equilibrium relation, <math>~\nabla P_0 = - \rho_0\nabla\Phi_0</math>, gives,

<math>~ \frac{\partial^2 \rho_1}{\partial t^2} - \nabla^2 P_1 - 4\pi G \rho_0 \rho_1 - \nabla\rho_0\cdot\nabla\Phi_1 </math>	<math>~=</math>	<math>~ \frac{\nabla\rho_0}{\rho_0} \cdot \biggl[ \nabla P_1 + \rho_1 \nabla \Phi_0 \biggr] + \rho_0 \nabla P_1 \cdot \nabla \biggl(\frac{1}{\rho_0} \biggr) + \rho_0\nabla \cdot \biggl[ \frac{\rho_1}{\rho_0} \nabla \Phi_0 \biggr] </math>
	<math>~=</math>	<math>~ \frac{\nabla\rho_0}{\rho_0} \cdot \biggl[ \nabla P_1 \biggr] + \frac{\rho_1}{\rho_0} \biggl[ \nabla\rho_0\cdot \nabla \Phi_0 \biggr] - \frac{1}{\rho_0} \nabla P_1 \cdot \nabla \rho_0 + \rho_0 \nabla \Phi_0 \cdot \nabla \biggl[ \frac{\rho_1}{\rho_0} \biggr] + \rho_1\nabla^2 \Phi_0 </math>
	<math>~=</math>	<math>~ \frac{\rho_1}{\rho_0} \biggl[ \nabla\rho_0\cdot \nabla \Phi_0 \biggr] - \frac{\rho_1}{\rho_0} \biggl[ \nabla \Phi_0 \cdot \nabla\rho_0\biggr] + \nabla \Phi_0 \cdot \nabla \rho_1 + 4\pi G \rho_0 \rho_1 </math>

<math>~\Rightarrow ~~~ \frac{\partial^2 \rho_1}{\partial t^2} - \nabla^2 P_1 - 8\pi G \rho_0 \rho_1 - \nabla\rho_0\cdot\nabla\Phi_1 - \nabla \Phi_0 \cdot \nabla \rho_1 </math>

This is identical to Yabushita's (1968) equation (2.12).

Taff and Van Horn (1974)

Drawing on the expressions for the radial profiles of various physical variables in equilibrium isothermal spheres, as provided above, our more familiar, "key" form of the wave equation can be rewritten as,

<math>~0</math>	<math>~=</math>	<math>~\frac{\xi^2}{r_0^2}\biggl\{ \frac{d^2x}{d\xi^2} + \biggl[4 - \biggl(\frac{r_0 g_0 \rho_0}{P_0}\biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)\biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x\biggr\} </math>
	<math>~=</math>	<math>~\frac{\xi^2}{r_0^2}\biggl\{ \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \frac{1}{4\pi G \rho_c \gamma_\mathrm{g}} \biggl[\omega^2 + (4 - 3\gamma_\mathrm{g}) \frac{4\pi G \rho_c }{\xi} \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] x\biggr\} </math>
	<math>~=</math>	<math>~\frac{4\pi G \rho_c}{\gamma_\mathrm{g} c_s^2} \biggl\{ \gamma_\mathrm{g}\frac{d^2x}{d\xi^2} + \gamma_\mathrm{g}\biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[\frac{\sigma_c^2}{6} - (3\gamma_\mathrm{g} - 4)~ \frac{1 }{\xi} \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] x\biggr\} </math>

Aside from the leading (constant) coefficient, this expression is identical to the linearized wave equation that Taff & Van Horn (1974) used to examine the radial pulsation modes of pressure-truncated isothermal spheres; their governing relation is displayed in the following, boxed-in image:

Equation extracted from p. 427 of L. G. Taff & H. M. Van Horn (1974, MNRAS, 168, 427-432)

"Radial Pulsations of Finite Isothermal Gas Spheres"

MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society

A mapping between our expression and the one copied directly from Taff & Van Horn (1974) is facilitated by the variable mapping provided here in Table 2; note, in particular, that the roles of the two variables, <math>~x</math> and <math>~\xi</math> are swapped.

Table 2: Mapping from Taff & Van Horn's (1974) Notation to Ours
Taff & Van Horn's (1974) Notation:	<math>~x</math>	<math>~\xi</math>	<math>~\psi</math>	<math>~\Gamma_1</math>	<math>~\lambda^2</math>
Our Notation:	<math>~\xi</math>	<math>~x</math>	<math>~\psi</math>	<math>~\gamma_\mathrm{g}</math>	<math>~\sigma_c^2/6</math>

Yabushita's (1992) Analysis

In the portion (§5) of his analysis that is focused on the stability of pressure-truncated polytropic spheres, S. Yabushita (1992) examined the eigenvalue problem governed by the following wave equation:

Radial Pulsation Equation Extracted^† from p. 182 of S. Yabushita (1992)

"Similarity Between the Structure and Stability of Isothermal and Polytropic Gas Spheres"

^†Equations and text displayed here exactly as it appears in the original publication.

Let's examine the overlap between this pair of governing relations and the ones employed by HRW66. If we replace the variable <math>~X</math> with <math>~h</math>, set <math>~\gamma = (n+1)/n</math>, and set the dimensionless eigenfrequency, <math>~s</math>, to zero in the radial pulsation equation employed by HRW66, we have,

<math>~0 </math>	<math>~=</math>	<math>~ \frac{d^2 h}{dx^2} + \biggl[\frac{4}{x} + (n+1) \frac{\theta^'}{\theta} \biggr] \frac{dh}{dx} + (n+1)\biggl[ 3 - \frac{4n}{(n+1)} \biggr] \biggl[ \frac{\theta^' h}{\theta x} \biggr] </math>
	<math>~=</math>	<math>~ \frac{d^2 h}{dx^2} + \biggl[\frac{4}{x} + (n+1) \frac{\theta^'}{\theta} \biggr] \frac{dh}{dx} + (3-n) \biggl[ \frac{\theta^' h}{\theta x} \biggr] \, . </math>

This matches equation (5.3) of Yabushita (1992) — see the above boxed-in image — except the <math>~(4/x)</math> term appears as <math>~(2/x)</math> in Yabushita's article; giving the benefit of the doubt, this is most likely a typographical error in Yabushita (1992). According to HRW66, the corresponding central boundary condition is,

While — after changing the sign on the right-hand side of HRW66's equation (58) as argued in our accompanying discussion in order to align with the separate derivations presented by Christy (1965) and Cox (1967) — the corresponding boundary condition at the surface is,

<math>~\frac{dh}{dx}</math>	<math>~=</math>	<math>~- \frac{h}{x} \biggr[ 3 - \frac{4}{\gamma} + \cancelto{0}{\frac{x s^2}{\gamma q}} \biggr]</math>
	<math>~=</math>	<math>~\frac{n-3}{n+1} \biggl(\frac{h}{x} \biggr) \, .</math>	at	<math>~x = x_0 \, .</math>

This surface boundary condition, which has been used by the astrophysics community in the context of isolated polytropic configurations, is different from the one displayed as equation (5.4) of Yabushita (1992). The surface boundary condition chosen by Yabushita — effectively,

— does seem to be more appropriate in the context of a study of the stability of pressure-truncated polytropes because, as argued by Ledoux & Pekeris (1941) and as reviewed in our accompanying discussion, it ensures that the pressure fluctuation at the surface is zero. It is worth noting that Yabushita's surface boundary condition matches the surface boundary condition chosen by Taff & Van Horn (1974) in their study of pressure-truncated isothermal spheres; in their words (see p. 428 of their article): [Setting the surface logarithmic derivative to negative 3] expresses the condition that the pressure at the perturbed surface always remain[s] equal to the confining pressure exerted by the external medium in which the [pressure-truncated] sphere must be embedded.

Numerical Integration from the Center, Outward

Here we show how a relatively simple, finite-difference algorithm can be developed to numerically integrate the governing LAWE from the center of the isothermal configuration, outward to its surface, which we will mark by the radial location, <math>~\xi_\mathrm{surf}</math>.

Following a parallel discussion, in preparation for discretization on a discrete radial grid, <math>~0 \le \xi_i \le \xi_\mathrm{surf}</math>, the above-defined LAWE for an isothermal may be written as,

<math>~ - \biggl[4 - \xi_i \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \frac{x_i'}{\xi_i} - \biggl[ \frac{\sigma_c^2}{6\gamma} - \frac{\alpha}{\xi} \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] x_i \, . </math>

Now, using the general finite-difference approach described separately, we make the substitutions,

<math>~\approx</math>

<math>~ \frac{x_+ - x_-}{2 \Delta_\xi} \, ; </math>

and,

<math>~\approx</math>

<math>~\frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \, ,</math>

which will provide an approximate expression for <math>~x_+ \equiv x_{i+1}</math>, given the values of <math>~x_- \equiv x_{i-1}</math> and <math>~x_i</math>. Specifically, if the center of the configuration is denoted by the grid index, <math>~i=1</math>, then for zones, <math>~i = 3 \rightarrow N</math>,

<math>~\frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} </math>	<math>~=</math>	<math>~ - \biggl[4 - \xi_i \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \frac{1}{\xi_i} \biggl[ \frac{x_+ - x_-}{2 \Delta_\xi}\biggr] - \biggl[ \frac{\sigma_c^2}{6\gamma} - \frac{\alpha}{\xi} \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] x_i </math>
<math>~\Rightarrow ~~~ x_+\biggl\{ \frac{1 }{\Delta_\xi^2} + \biggl[4 - \xi_i \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \frac{1}{\xi_i} \biggl[ \frac{1}{2 \Delta_\xi}\biggr] \biggr\} </math>	<math>~=</math>	<math>~ x_- \biggl\{ \biggl[4 - \xi_i \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \frac{1}{\xi_i} \biggl[ \frac{1}{2 \Delta_\xi}\biggr] - \frac{1 }{\Delta_\xi^2} \biggr\} + x_i \biggl\{ \frac{2}{\Delta_\xi^2} - \biggl[ \frac{\sigma_c^2}{6\gamma} - \frac{\alpha}{\xi} \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \biggr\} </math>
<math>~\Rightarrow ~~~ x_+\biggl\{ 2 + \biggl[4 - \xi_i \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \frac{\Delta_\xi}{\xi_i} \biggr\} </math>	<math>~=</math>	<math>~ x_- \biggl\{ \biggl[4 - \xi_i \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \frac{\Delta_\xi}{\xi_i} - 2 \biggr\} + x_i \biggl\{ 4 - 2\Delta_\xi^2 \biggl[ \frac{\sigma_c^2}{6\gamma} - \frac{\alpha}{\xi} \biggl(\frac{d\psi }{d\xi}\biggr)_i \biggr] \biggr\} </math>

At the very center <math>~(\xi_1=0)</math>, we will set <math>~x_1=1</math>; then at the first radial grid line off the center <math>~(\xi_2 = \Delta_\xi)</math>, we will call upon the derived series expansion to set,

<math>~1-\frac{\mathfrak{F}\Delta_\xi^2}{60} \, .</math>

User:Tohline/SSC/Stability/Isothermal

Contents

Radial Oscillations of Pressure-Truncated Isothermal Spheres

Groundwork

Equilibrium Model

Linearized Wave Equation

Yabushita (1968)

Taff and Van Horn (1974)

Yabushita's (1992) Analysis

Numerical Integration from the Center, Outward

See Also

Navigation menu

Search