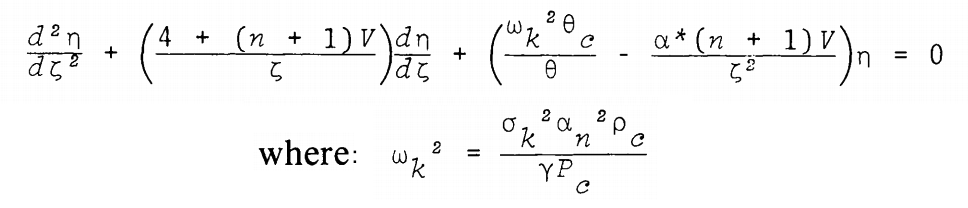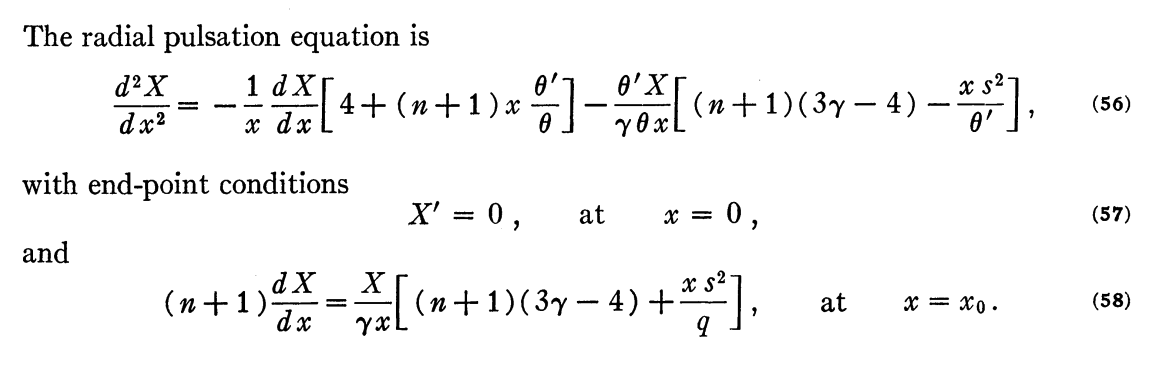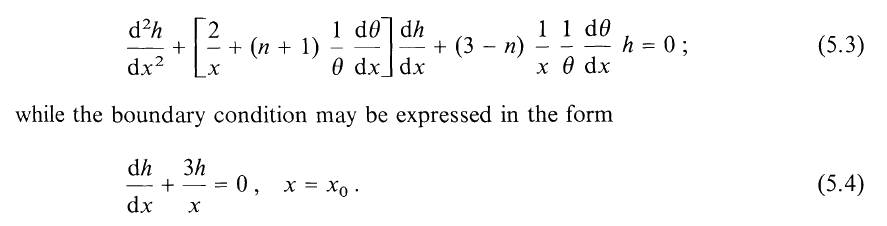User:Tohline/SSC/Stability/Polytropes

Radial Oscillations of Polytropic Spheres

Groundwork

Adiabatic (Polytropic) Wave Equation

In an accompanying discussion, we derived the so-called,

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. If the initial, unperturbed equilibrium configuration is a polytropic sphere whose internal structure is defined by the function, <math>~\theta(\xi)</math>, then

<math>~r_0</math>	<math>~=</math>	<math>~a_n \xi \, ,</math>
<math>~\rho_0</math>	<math>~=</math>	<math>~\rho_c \theta^{n} \, ,</math>
<math>~P_0</math>	<math>~=</math>	<math>~K\rho_0^{(n+1)/n} = K\rho_c^{(n+1)/n} \theta^{n+1} \, ,</math>
<math>~g_0</math>	<math>~=</math>	<math>~\frac{GM(r_0)}{r_0^2} = \frac{G}{r_0^2} \biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math>

where,

<math>~a_n</math>

<math>~=</math>

<math>~\biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \, .</math>

Hence, after multiplying through by <math>~a_n^2</math>, the above adiabatic wave equation can be rewritten in the form,

<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{g_0}{a_n}\biggl(\frac{a_n^2 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\xi} + \biggl(\frac{a_n^2\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{a_n\xi} \biggr] x </math>

<math>~=</math>

<math>~0 \, .</math>

In addition, given that,

<math>~\frac{g_0}{a_n}</math>

<math>~=</math>

<math>~4\pi G \rho_c \biggl(-\frac{d \theta}{d\xi} \biggr) \, ,</math>

and,

<math>~\frac{a_n^2 \rho_0}{P_0}</math>

<math>~=</math>

<math>~\frac{(n+1)}{(4\pi G\rho_c)\theta} = \frac{a_n^2 \rho_c}{P_c} \cdot \frac{\theta_c}{\theta}\, ,</math>

we can write,

<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>

<math>~=</math>

<math>0 \, ,</math>

where we have adopted the function notation,

<math>~V(\xi)</math>

<math>~\equiv</math>

<math>~- \frac{\xi}{\theta} \frac{d \theta}{d\xi} \, .</math>

As can be seen in the following framed image, this is the form of the polytropic wave equation published by J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222), at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models." (NOTE: There appears to be a sign error in the numerator of the second term of their published expression; there also appears to be an error in the definition of the coefficient, <math>~\alpha^*</math>, as given in the text of their paper.)

Polytropic Wave Equation extracted† from J. O. Murphy & R. Fiedler (1985b) "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models" Proceeding of the Astronomical Society of Australia, vol. 6, pp. 222 - 226 © Astronomical Society of Australia
†Equations displayed here, as a single digital image, with layout modified from the original publication.

It is also the same as the radial pulsation equation for polytropic configurations that appears as equation (56) in the detailed discussion of "The Oscillations of Gas Spheres" published by H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535); hereafter, we will refer to this paper as HRW66. The relevant set of equations from HRW66 has been extracted as a single digital image and reprinted, here, as a boxed-in image.

Radial Pulsation Equation as Presented† by M. Hurley, P. H. Roberts, & K. Wright (1966) "The Oscillations of Gas Spheres" The Astrophysical Journal, vol. 143, pp. 535 - 551 © American Astronomical Society
†Set of equations and accompanying text displayed here, as a single digital image, exactly as they appear in the original publication.

In order to make clearer the correspondence between our derived expression and the one published by HRW66, we will rewrite the HRW66 radial pulsation equation: (1) Gathering all terms on the same side of the equation; (2) making the substitution,

<math>\theta^' \rightarrow -\frac{\theta V}{x} \, ;</math>

and (3) reattaching a "prime" to the quantity, <math>~s</math>, to emphasize that it is a dimensionless frequency.

ASIDE: In their equation (46), HRW66 convert the eigenfrequency, <math>~s</math> — which has units of inverse time — to a dimensionless eigenfrequency, <math>~s^'</math>, via the relation, <math>~s = \biggl( \frac{4\pi G \rho_c}{1+n} \biggr)^{1/2} s^' ~~~~~~~\cdots\cdots~~~~~~~(46)</math> Then, immediately following equation (46), they state that they will "omit the prime on <math>~s</math> henceforward." As a result, the dimensionless eigenfrequency that appears in their equations (56) and (58) is unprimed. This is unfortunate as it somewhat muddies our efforts, here, to demonstrate the correspondence between the HRW66 polytropic radial pulsation equation and ours. In our subsequent manipulation of equation (56) from HRW66 we reattach a prime to the quantity, <math>~s</math>, to emphasize that it is a dimensionless frequency. But this prime on <math>~s</math> should not be confused with the prime on <math>~\theta</math> (HRW66 equation 56) or with the prime on <math>~X</math> (HRW66 equation 57), both of which denote differentiation with respect to the radial coordinate.

With these modifications, the HRW66 radial pulsation equation becomes,

<math>~0</math>	<math>~=</math>	<math> ~\frac{d^2 X}{dx^2} + \biggl[\frac{4 - (n+1)V }{x}\biggr]\frac{dX}{dx} - \frac{V}{\gamma x^2}\biggl[\frac{x^2 (s^')^2}{\theta V} + (3\gamma -4)(n+1) \biggr]X </math>
	<math>~=</math>	<math> ~\frac{d^2 X}{dx^2} + \biggl[\frac{4 - (n+1)V }{x}\biggr]\frac{dX}{dx} + \biggl[-\frac{(s^')^2 }{\gamma \theta } - \biggl(3 -\frac{4}{\gamma}\biggr)\frac{(n+1)V}{x^2} \biggr]X \, . </math>

The correspondence with our derived expression is complete, assuming that,

<math>~(s^')^2</math>	<math>~=</math>	<math>~-\omega^2 \biggl(\frac{a_n^2 \rho_c }{P_c} \biggr) \theta_c</math>
	<math>~=</math>	<math>~-\omega^2 \biggl[\frac{n+1 }{4\pi G \rho_c} \biggr] \, .</math>

As has been explained in the above "ASIDE," this is exactly the factor that HRW66 use to normalize their eigenfrequency, <math>~s</math>, and make it dimensionless <math>~(s^')</math>. It is clear, as well, that HRW66 have adopted a sign convention for the square of their eigenfrequency that is the opposite of the sign convention that we have adopted for <math>~\omega^2</math>. That is, it is clear that,

<math>~s^2 ~~\leftrightarrow~~ - \omega^2 \, .</math>

Boundary Conditions

As we have pointed out in the context of a general discussion of boundary conditions associated with the adiabatic wave equation, the eigenfunction, <math>~x</math>, will be suitably well behaved at the center of the configuration if,

<math>~\frac{dx}{dr_0} = 0</math>        at         <math>~r_0 = 0 \, ,</math>

which, in the context of our present discussion of polytropic configurations, leads to the inner boundary condition,

<math>~\frac{dx}{d\xi} = 0</math>        at         <math>~\xi = 0 \, .</math>

This is precisely the inner boundary condition specified by HRW66 — see their equation (57), which has been reproduced in the above excerpt from HWR66.

As we have also shown in the context of this separate, general discussion of boundary conditions associated with the adiabatic wave equation, the pressure fluctuation will be finite at the surface — even if the equilibrium pressure and/or the pressure scale height go to zero at the surface — if the radial eigenfunction, <math>~x</math>, obeys the relation,

<math>~r_0 \frac{dx}{dr_0}</math>

<math>~=</math>

<math>~\biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) \frac{x}{\gamma_g}</math>        at         <math>~r_0 = R \, .</math>

Or, given that, in polytropic configurations, <math>~r_0 = a_n\xi</math>,

<math>~\xi \frac{dx}{d\xi}</math>

<math>~=</math>

<math>~\frac{x}{\gamma_g} \biggl[ 4 - 3\gamma_g + \frac{\omega^2 (a_n \xi_1)^3}{GM_\mathrm{tot}}\biggr] </math>        at         <math>~\xi = \xi_1 \, ,</math>

where, the subscript "1" denotes equilibrium, surface values. As can be deduced from our above summary of the properties of polytropic configurations,

<math>~GM_\mathrm{tot}</math>

<math>~=</math>

<math>~4\pi G a_n^3 \rho_c (-\xi_1^2 \theta_1^') \, .</math>

Hence, for spherically symmetric polytropic configurations, the surface boundary condition becomes,

<math>~\frac{dx}{d\xi}</math>	<math>~=</math>	<math>~\frac{x}{\gamma_g \xi} \biggl[ 4 - 3\gamma_g + \omega^2 \biggl( \frac{1}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')}\biggr] </math>         at         <math>~\xi = \xi_1 \, ,</math>
<math>~\Rightarrow ~~~~~(n+1)\frac{dx}{d\xi}</math>	<math>~=</math>	<math>~\frac{x}{\gamma_g \xi} \biggl[ (n+1)(4 - 3\gamma_g) + \omega^2 \biggl( \frac{1+n}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')}\biggr] </math>
	<math>~=</math>	<math>~-\frac{x}{\gamma_g \xi} \biggl[ (n+1)(3\gamma_g-4) - \omega^2 \biggl( \frac{1+n}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')}\biggr] </math>         at         <math>~\xi = \xi_1 \, .</math>

Adopting notation used by HRW66, specifically, as demonstrated above,

<math>~-\omega^2 \biggl( \frac{1+n}{4\pi G \rho_c } \biggr) \rightarrow (s^')^2 \, , </math>

and, from equation (50) of HRW66,

<math>~-\theta^' \rightarrow q </math>         at         <math>~\xi = \xi_1 \, ,</math>

this outer boundary condition becomes,

<math>~(n+1)\frac{dx}{d\xi}</math>

<math>~=</math>

<math>~-\frac{x}{\gamma_g \xi} \biggl[ (n+1)(3\gamma_g-4) + \frac{\xi (s^')^2}{q}\biggr] </math>         at         <math>~\xi = \xi_1 \, .</math>

With the exception of the leading negative sign on the right-hand side, this expression is identical to the outer boundary condition identified by equation (58) of HRW66 — see the excerpt reproduced above.

Yabushita's (1992) Analysis

In the portion (§5) of his analysis that is focused on the stability of pressure-truncated polytropic spheres, S. Yabushita (1992) examined the eigenvalue problem governed by the following wave equation:

Radial Pulsation Equation Extracted† from p. 182 of S. Yabushita (1992) "Similarity Between the Structure and Stability of Isothermal and Polytropic Gas Spheres" Astrophysics and Space Science, vol. 193, pp. 173-183 © Springer
†Equations and text displayed here exactly as it appears in the original publication.

Let's examine the overlap between this pair of governing relations and the ones employed by HRW66. If we replace the variable <math>~X</math> with <math>~h</math>, set <math>~\gamma = (n+1)/n</math>, and set the dimensionless eigenfrequency, <math>~s</math>, to zero in the radial pulsation equation employed by HRW66, we have,

<math>~0 </math>	<math>~=</math>	<math>~ \frac{d^2 h}{dx^2} + \biggl[\frac{4}{x} + (n+1) \frac{\theta^'}{\theta} \biggr] \frac{dh}{dx} + (n+1)\biggl[ 3 - \frac{4n}{(n+1)} \biggr] \biggl[ \frac{\theta^' h}{\theta x} \biggr] </math>
	<math>~=</math>	<math>~ \frac{d^2 h}{dx^2} + \biggl[\frac{4}{x} + (n+1) \frac{\theta^'}{\theta} \biggr] \frac{dh}{dx} + (3-n) \biggl[ \frac{\theta^' h}{\theta x} \biggr] \, . </math>

This matches equation (5.3) of Yabushita (1992) — see the above boxed-in image — except the <math>~(4/x)</math> term appears as <math>~(2/x)</math> in Yabushita's article; giving the benefit of the doubt, this is most likely a typographical error in Yabushita (1992). According to HRW66, the corresponding central boundary condition is,

<math>\frac{dh}{dx} = 0</math>         at         <math>x=0 \, .</math>

While — after changing the sign on the right-hand side of HRW66's equation (58) as argued in our accompanying discussion in order to align with the separate derivations presented by Christy (1965) and Cox (1967) — the corresponding boundary condition at the surface is,

<math>~\frac{dh}{dx}</math>	<math>~=</math>	<math>~- \frac{h}{x} \biggr[ 3 - \frac{4}{\gamma} + \cancelto{0}{\frac{x s^2}{\gamma q}} \biggr]</math>
	<math>~=</math>	<math>~\frac{n-3}{n+1} \biggl(\frac{h}{x} \biggr) \, .</math>	at	<math>~x = x_0 \, .</math>

This surface boundary condition, which has been used by the astrophysics community in the context of isolated polytropic configurations, is different from the one displayed as equation (5.4) of Yabushita (1992). The surface boundary condition chosen by Yabushita — effectively,

<math>~\frac{d \ln h}{d\ln x} = -3 \, ,</math>

— does seem to be more appropriate in the context of a study of the stability of pressure-truncated polytropes because, as argued by Ledoux & Pekeris (1941) and as reviewed in our accompanying discussion, it ensures that the pressure fluctuation at the surface is zero. It is worth noting that Yabushita's surface boundary condition matches the surface boundary condition chosen by Taff & Van Horn (1974) in their study of pressure-truncated isothermal spheres; in their words (see p. 428 of their article):   [Setting the surface logarithmic derivative to negative 3] expresses the condition that the pressure at the perturbed surface always remain[s] equal to the confining pressure exerted by the external medium in which the [pressure-truncated] sphere must be embedded.

Overview

The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications:

• P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) —
• R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353) — Pulsation Theory
• M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535) — The Oscillations of Gas Spheres
• J. P. Cox (1974, Reports on Progress in Physics, 37, 563) — Pulsating Stars

Tables

Quantitative Information Regarding Eigenvectors of Oscillating Polytropes <math>~(\Gamma_1 = 5/3)</math>
<math>~n</math>	<math>~\frac{\rho_c}{\bar\rho}</math>	Excerpts from Table 1 of Hurley, Roberts, & Wright (1966) <math>~s^2 (n+1)/(4\pi G\rho_c)</math>	Excerpts from Table 3 of J. P. Cox (1974) <math>~\sigma_0^2 R^3/(GM)</math>	<math>\frac{(n+1) *\mathrm{Cox74}}{3 *\mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math>
<math>~0</math>	<math>~1</math>	<math>~1/3</math>	<math>~1</math>	<math>~1</math>
<math>~1</math>	<math>~3.30</math>	<math>~0.38331</math>	<math>~1.892</math>	<math>~0.997</math>
<math>~1.5</math>	<math>~5.99</math>	<math>~0.37640</math>	<math>~2.712</math>	<math>~1.002</math>
<math>~2</math>	<math>~11.4</math>	<math>~0.35087</math>	<math>~4.00</math>	<math>~1.000</math>
<math>~3</math>	<math>~54.2</math>	<math>~0.22774</math>	<math>~9.261</math>	<math>~1.000</math>
<math>~3.5</math>	<math>~153</math>	<math>~0.12404</math>	<math>~12.69</math>	<math>~1.003</math>
<math>~4.0</math>	<math>~632</math>	<math>~0.04056</math>	<math>~15.38</math>	<math>~1.000</math>

n = 5 Polytrope

Setup Using Lagrangian Radial Coordinate

Individual Terms

From our accompanying discussion, we have, for pressure-truncated, <math>~n=5</math> polytropic spheres

<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{4\pi}{(n+1)^n}\biggr]^{1/(n-3)} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} </math>
	<math>~=~</math>	<math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{-2} \, , </math>

which matches the expression derived in an ASIDE box found with our introduction of the Lane-Emden equation, and

<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{(n+1)/(n-3)} \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} </math>
	<math>~=~</math>	<math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} \tilde\theta^{6}( -\tilde\xi^2 \tilde\theta' )^{6} \, , </math>

where,

<math>~R_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} = \biggl( \frac{G}{K} \biggr)^{5/2} M_\mathrm{tot}^{2} \, ,</math>
<math>~P_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} = \frac{K^{10}}{G^{9} M_\mathrm{tot}^{6} } \, ,</math>

and, from our more detailed analysis,

<math> ~{\tilde\theta}_5 = 3^{1 / 2} \biggl( 3 + {\tilde\xi}^2\biggr)^{-1/2} </math>

and

<math> ~\biggl(- {\tilde\xi}^2 {\tilde\theta}^'_5\biggr) = 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \, . </math>

Hence,

<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi \biggl[ 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \biggr]^{-2} </math>
	<math>~=~</math>	<math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi \biggl[ 3^{-1} {\tilde\xi}^{-6} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \biggr] </math>
	<math>~=~</math>	<math>~ \biggl[ \frac{4\pi}{2^5\cdot 3^7}\biggr]^{1/2} {\tilde\xi}^{-5} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \, , </math>
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} \biggl[ 3^{1 / 2} \biggl( 3 + {\tilde\xi}^2\biggr)^{-1/2} \biggr]^{6} \biggl[ 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \biggr]^{6} </math>
	<math>~=~</math>	<math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} \biggl[ 3^{3} \biggl( 3 + {\tilde\xi}^2\biggr)^{-3} \biggr] \biggl[ 3^{3} {\tilde\xi}^{18} \biggl( 3 + {\tilde\xi}^2\biggr)^{-9} \biggr] </math>
	<math>~=~</math>	<math>~\biggl[ \frac{2^3\cdot 3^5}{4\pi}\biggr]^{3} {\tilde\xi}^{18} \biggl( 3 + {\tilde\xi}^2\biggr)^{-12} \, . </math>

Now, given that the structural form-factors for <math>~n=5</math> configurations are,

<math>~\mathfrak{f}_M</math>	<math>~=</math>	<math>~ ( 1 + \ell^2 )^{-3/2} = 3^{3 / 2} (3 + {\tilde\xi}^2)^{-3 / 2} </math>
<math>~\mathfrak{f}_W</math>	<math>~=</math>	<math>~ \frac{5}{2^4} \cdot \ell^{-5} \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] </math>
<math>~\mathfrak{f}_A</math>	<math>~=</math>	<math>~ \frac{3}{2^3} \ell^{-3} [ \tan^{-1}(\ell ) + \ell (\ell^2-1) (1+\ell^2)^{-2} ] \, , </math>

we understand that the central density is,

<math>~\rho_c = \frac{\bar\rho}{ {\tilde\mathfrak{f}}_M }</math>	<math>~=</math>	<math>~ \biggl[3^{3 / 2} (3 + {\tilde\xi}^2)^{-3 / 2} \biggr]^{-1} \biggl[ \frac{3 M_\mathrm{tot}}{4 \pi R_\mathrm{eq}^3} \biggr] </math>
	<math>~=</math>	<math>~ \biggl( \frac{3}{4\pi}\biggr) \biggl[ \frac{2^5\cdot 3^6}{4\pi}\biggr]^{ 3 / 2} (3 + {\tilde\xi}^2)^{3 / 2} M_\mathrm{tot} \biggl[ R_\mathrm{norm} {\tilde\xi}^{-5} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \biggr]^{-3} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{2^{5}\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} {\tilde\xi}^{15} (3 + {\tilde\xi}^2)^{-15 / 2} M_\mathrm{tot} R^{-3}_\mathrm{norm} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{2^{5}\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} M_\mathrm{tot}^{-5} \biggl( \frac{G}{K} \biggr)^{-15/2} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \, . </math>

Now let's derive the prescription for the Lagrangian radial coordinate in the context of pressure-truncated, <math>~n=5</math> polytropes.

<math>~r_0 \equiv a_5 \xi</math>	<math>~=</math>	<math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \rho_c^{-2/5} \xi</math>
	<math>~=</math>	<math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \xi \biggl\{ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \biggr\}^{-2/5} </math>
	<math>~=</math>	<math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr] \biggl( \frac{G^3M_\mathrm{tot}^2}{K^3} \biggr) \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi </math>
	<math>~=</math>	<math>~ R_\mathrm{norm} \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi </math>

Also,

<math>~m_0 \equiv M(r_0)</math>	<math>~=</math>	<math>~\biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math>
	<math>~=</math>	<math>~2^2\pi \biggl\{ R_\mathrm{norm} \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \tilde\xi^{-6} (3 + {\tilde\xi}^2)^{3} \biggr\}^3 \biggl\{ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \biggr\} \biggl\{ 3^{1 / 2} \xi^3 \biggl( 3 + \xi^2\biggr)^{-3/2} \biggr\} </math>
	<math>~=</math>	<math>~ 3^{1 / 2} \biggl[ 2^4 \pi^2\biggr]^{1 / 2} \biggl[ \frac{\pi^3}{2^9\cdot 3^{21}}\biggr]^{1 / 2} \biggl[ \frac{2^5\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} \biggl\{ \tilde\xi^{-6} (3 + {\tilde\xi}^2)^{3} \biggr\}^3 \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} R_\mathrm{norm}^3 \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} </math>
	<math>~=</math>	<math>~ \biggl\{ \tilde\xi^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr\} M_\mathrm{tot} \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} \, . </math>

Hence,

<math>~g_0 = \frac{Gm_0}{r_0^2}</math>	<math>~=</math>	<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^2} \biggl\{ \tilde\xi^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr\} \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} \biggl\{ \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \biggr\}^{-2} </math>
	<math>~=</math>	<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^2}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl[ \tilde\xi (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{9} \xi ( 3 + \xi^2 )^{-3/2} \, ; </math>
<math>~\frac{g_0 }{r_0} </math>	<math>~=</math>	<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^3}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl\{ \tilde\xi^{9} (3 + {\tilde\xi}^2)^{-9 / 2} \biggr\} \biggl\{ \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \biggr\}^{-1} \xi ( 3 + \xi^2 )^{-3/2} </math>
	<math>~=</math>	<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^3}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{3/2} \biggl[ \tilde\xi (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} ( 3 + \xi^2 )^{-3/2} \, ; </math>

<math>~\frac{\rho_0}{P_0} = \frac{\rho_0}{K\rho_0^{1+1/n}} </math>	<math>~=</math>	<math>~ \biggl[K^5 \rho_c \theta^5 \biggr]^{-1/5} </math>
	<math>~=</math>	<math>~ \theta^{-1} \biggl\{ K^5 \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2}\biggr\}^{-1/5} </math>
	<math>~=</math>	<math>~ \biggl[ 3^{-1} ( 3 + \xi^2 ) \biggr]^{1/2} \biggl\{ \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr]^{1 / 2} \cancelto{\mathrm{mistake}}{\biggl[{\tilde\xi}^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr]^{-3} } \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggr\} </math>
	<math>~=</math>	<math>~ \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1 / 2} \biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \cancelto{\mathrm{mistake}}{\biggl[ {\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{9} } ( 3 + \xi^2 )^{1 / 2} \, ; </math>
	<math>~=</math>	<math>~ \biggl[ 3^{-1} ( 3 + \xi^2 ) \biggr]^{1/2} \biggl\{ \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr]^{1 / 2} \biggl[{\tilde\xi}^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr] \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggr\} </math>
	<math>~=</math>	<math>~ \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{3 / 2} ( 3 + \xi^2 )^{1/2} </math>
<math>~\frac{g_0\rho_0}{P_0} </math>	<math>~=</math>	<math>~ \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{3 / 2} ( 3 + \xi^2 )^{1/2} </math>
		<math>~ \times ~ \biggl( \frac{G^2M_\mathrm{tot}^2}{R_\mathrm{norm}^4} \biggr)^{1 / 2}\biggl[ \frac{2^6\cdot 3^{14}}{\pi^2}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{-9 / 2} \xi ( 3 + \xi^2 )^{-3/2} </math>
	<math>~=</math>	<math>~ \biggl( \frac{G^5 M_\mathrm{tot}^4}{K^5} \biggr)^{1 / 2} R_\mathrm{norm}^{-2} \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1} </math>
	<math>~=</math>	<math>~ \biggl( \frac{K^5}{G^5 M_\mathrm{tot}^4} \biggr)^{1 / 2} \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1} \, . </math>

The Wave Equation

Starting from our Key Adiabatic Wave Equation

The adiabatic wave equation therefore becomes,

<math>~0</math>	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x </math>
	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_\mathrm{norm}} \biggl\{ \biggl[ \frac{2^7\cdot 3^{7}}{\pi} \biggr]^{1 / 2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \frac{1}{\xi} - \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1} \biggr\} \frac{dx}{dr_0} </math>
		<math>~ + \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g R_\mathrm{norm}^2} \biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-3/2} ( 3 + \xi^2 )^{1 / 2} \biggl\{ \frac{R_\mathrm{norm}^3}{GM_\mathrm{tot}} \biggl[\frac{\omega^2}{(4 - 3\gamma_\mathrm{g})} \biggr] + \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{3/2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{15/2} ( 3 + \xi^2 )^{-3/2} \biggr\} x </math>
	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_\mathrm{norm}} \biggl[ \frac{2^3\cdot 3^{7}}{\pi} \biggr]^{1 / 2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{dr_0} </math>
		<math>~ + \frac{6(4 - 3\gamma_\mathrm{g})}{\gamma_g R_\mathrm{norm}^2} ( 3 + \xi^2 )^{1 / 2} \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{ \frac{R_\mathrm{norm}^3}{GM_\mathrm{tot}} \biggl[\frac{\omega^2}{(4 - 3\gamma_\mathrm{g})} \biggr] \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{-3/2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-15/2} + ( 3 + \xi^2 )^{-3/2} \biggr\} x </math>
	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{dr_0} + \frac{6}{\gamma_g R_*^2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{ \frac{\omega^2 R_*^3}{GM_\mathrm{tot}} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-15/2}( 3 + \xi^2 )^{1 / 2} + \frac{(4 - 3\gamma_\mathrm{g})}{( 3 + \xi^2 ) } \biggr\} x </math>

where,

<math>R_* \equiv R_\mathrm{norm} \biggl[ \frac{\pi}{2^3 \cdot 3^7} \biggr]^{1/2} \, .</math>

Recognizing that,

<math>~r_0</math>

<math>~=</math>

<math>~ R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \, , </math>

we can write,

<math>~0</math>

<math>~=</math>

<math>~\frac{1}{R_*^2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{ \frac{d^2x}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{d\xi} + \frac{6}{\gamma_g } \biggl[\sigma^2 ( 3 + \xi^2 )^{1 / 2} + \frac{(4 - 3\gamma_\mathrm{g})}{( 3 + \xi^2 ) } \biggr] x \biggr\} \, , </math>

where,

<math>~\sigma^2</math>

<math>~\equiv</math>

<math>~ \frac{\omega^2 R_*^3}{GM_\mathrm{tot}} \biggl( \frac{3 + {\tilde\xi}^2}{{\tilde\xi}^2} \biggr)^{15/2} \, .</math>

Finally, if — because we are specifically considering the case of <math>~n=5</math> — we set <math>~\gamma_\mathrm{g} = 1 + 1/n = 6/5</math>, we have,

<math>~0</math>	<math>~=</math>	<math>~ \frac{d^2x}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{d\xi} + \biggl[5\sigma^2 ( 3 + \xi^2 )^{1 / 2} + \frac{2}{( 3 + \xi^2 ) }\biggr] x </math>
	<math>~=</math>	<math>~\frac{1}{( 3 + \xi^2 ) } \biggl\{ ( 3 + \xi^2 )\frac{d^2x}{d\xi^2} + \biggl[ \frac{2(6 - \xi^2) }{ \xi} \biggr] \frac{dx}{d\xi} + \biggl[5\sigma^2 ( 3 + \xi^2 )^{3 / 2} + 2 \biggr] x \biggr\} \, . </math>

Starting from the HRW66 Radial Pulsation Equation

More directly, if we begin with the HRW66 radial pulsation equation that is already tuned to polytropic configurations, the wave equation appropriate to <math>~n=5</math> polytropes is,

<math>~0</math>	<math>~=</math>	<math>~ \frac{d^2 X}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 (-\theta^'_5)}{\theta_5} \biggr]\frac{d X}{d\xi} + \frac{5(-\theta_5^') }{6\theta_5 \xi} \bigg[ \frac{\xi (s^')^2}{\theta^'_5} + \frac{12}{5} \biggr] X </math>
	<math>~=</math>	<math>~ \frac{d^2 X}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{(3 + \xi^2)} \biggr]\frac{d X}{d\xi} + \frac{1}{(3 + \xi^2)} \bigg[ -\frac{5(s^')^2(3 + \xi^2)^{3 / 2}}{2 \cdot 3^{3 / 2}} + 2 \biggr] X </math>
	<math>~=</math>	<math>~\frac{1}{(3+\xi^2)} \biggl\{ (3+\xi^2)\frac{d^2 X}{d\xi^2} + \biggl[ \frac{2(6-\xi^2)}{\xi}\biggr]\frac{d X}{d\xi} + \bigg[ -\frac{5(s^')^2}{2 \cdot 3^{3 / 2}} \cdot (3 + \xi^2)^{3 / 2} + 2 \biggr] X \biggr\} \, , </math>

which is identical to the brute-force derivation just presented, allowing for the mapping,

<math>\sigma^2 ~~ \Leftrightarrow ~~ -\frac{(s^')^2}{2 \cdot 3^{3 / 2}} \, .</math>

New Independent Variable

Guided by our conjecture regarding the proper shape of the radial eigenfunction, let's switch the dependent variable to,

<math>~u \equiv 1 + \frac{3}{\xi^2}</math>

<math>~\Rightarrow</math>

<math>~3 + \xi^2 = \frac{3u}{(u-1)} \, ,</math>

and

<math>~\xi = 3^{1 / 2} (u-1)^{-1 / 2} \, .</math>

This implies that,

<math>~\frac{d}{d\xi}</math>

<math>~~~\rightarrow ~~~</math>

<math>~-\frac{2}{\sqrt{3}}(u-1)^{3 / 2} \frac{d}{du} \, ,</math>

and,

<math>~\frac{d^2}{d\xi^2}</math>

<math>~~~\rightarrow ~~~</math>

<math>~\frac{4}{3}(u-1)^3 \frac{d^2}{du^2} + 2(u-1)^{2} \frac{d}{du} \, .</math>

Hence, the governing wave equation becomes,

<math>~0</math>	<math>~=</math>	<math>~( 3 + \xi^2 )\frac{d^2x}{d\xi^2} + \biggl[ \frac{2(6 - \xi^2) }{ \xi} \biggr] \frac{dx}{d\xi} + \biggl[5\sigma^2 ( 3 + \xi^2 )^{3 / 2} + 2 \biggr] x </math>
	<math>~=</math>	<math>~\frac{3u}{(u-1)} \biggl[\frac{4}{3}(u-1)^3 \frac{d^2x}{du^2} + 2(u-1)^{2} \frac{dx}{du}\biggr] + 4(2u-3)(u-1)\frac{dx}{du} + \biggl\{ 5\sigma^2 \biggl[ \frac{3u}{(u-1)} \biggr]^{3 / 2} + 2 \biggr\} x </math>
	<math>~=</math>	<math>~4u(u-1)^2 \frac{d^2x}{du^2} + (14u-12)(u-1)\frac{dx}{du} + \biggl\{ 5\sigma^2 \biggl[ \frac{3u}{(u-1)} \biggr]^{3 / 2} + 2 \biggr\} x \, . </math>

If we assume that <math>~\sigma^2 = 0</math>, then the governing relation is,

<math>~0</math>

<math>~=</math>

<math>~4u(u-1)^2 \frac{d^2x}{du^2} + (14u-12)(u-1)\frac{dx}{du} + 2 x \, . </math>

Now, again, guided by our conjecture, let's guess an eigenfunction of the form:

First Guess (n5)

<math>~x</math>

<math>~=</math>

<math>~ A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} \, , </math>

in which case,

<math>~\frac{dx}{du}</math>	<math>~=</math>	<math>~ \frac{A^3}{2} \biggl[ (u - 1)^{-1 / 2} (A u - 1 )^{-1 / 2} - A(u - 1)^{1 / 2} (A u - 1 )^{-3 / 2} \biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-1 / 2} (Au-1)^{-3 / 2} \, ; </math>
<math>~\frac{d^2x}{du^2}</math>	<math>~=</math>	<math>~ \biggl[ \frac{A^3(A-1)}{2} \biggr] \biggl\{ -\frac{1}{2}(u-1)^{-3 / 2} (Au-1)^{-3 / 2} -\frac{3A}{2} (u-1)^{-1 / 2} (Au-1)^{-5 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{1}{2} \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[ (Au-1) +3A (u-1)\biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \frac{A^3(A-1)}{4} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] \, . </math>

So the governing relation becomes:

<math>~0</math>	<math>~=</math>	<math>~4u(u-1)^2 \biggl\{ \biggl[ \frac{A^3(A-1)}{4} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] \biggr\} </math>
		<math>~ + (14u-12)(u-1) \biggl\{ \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-1 / 2} (Au-1)^{-3 / 2} \biggr\} + 2 A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} </math>
	<math>~=</math>	<math>~u(u-1)^{1 / 2} A^3(A-1) (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] </math>
		<math>~ + (7u-6)(u-1)^{1 / 2} A^3(A-1) (Au-1)^{-3 / 2} + 2 A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} </math>
	<math>~=</math>	<math>~(u-1)^{1 / 2} \biggl\{ uA^3(A-1) (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] + (7u-6) A^3(A-1) (Au-1)^{-3 / 2} + 2 A^3 (A u - 1 )^{-1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ u(A-1) \biggl[(3A+1) - 4Au \biggr] + (7u-6) (A-1) (Au-1) + 2 (A u - 1 )^{2} \biggr\} </math>
	<math>~=</math>	<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ - 4u^2 A(A-1) + u(A-1) (3A+1) + (7u-6) [A(A-1)u +1 - A] + 2 (A^2u^2 - 2Au +1) \biggr\} </math>
	<math>~=</math>	<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ u^2 \biggl[ - 4A(A-1) +7A(A-1) +2A^2 \biggr] + u\biggl[ (A-1) (3A+1) - 7(A-1) -6A(A-1) - 4A \biggr] + 2(3A-2) \biggr\} </math>
	<math>~=</math>	<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ Au^2 \biggl[ 5A-3 \biggr] + u\biggl[ 3A^2-2A-1-7A+7 -6A^2+6A -4A \biggr] + 2(3A-2) \biggr\} \, . </math>
	<math>~=</math>	<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ Au^2 \biggl[ 5A-3 \biggr] + u\biggl[ -3A^2 -7A +6\biggr] + 2(3A-2) \biggr\} \, . </math>

Second Guess (n5)

<math>~x</math>

<math>~=</math>

<math>~ (u - 1)^{b / 2} (A u - 1 )^{-a / 2} \, , </math>

in which case,

<math>~\frac{dx}{du}</math>	<math>~=</math>	<math>~ \frac{b}{2}(u-1)^{b/2-1} (A u - 1 )^{-a / 2} - \frac{aA}{2}(u - 1)^{b / 2} (A u - 1 )^{-a / 2-1} </math>
	<math>~=</math>	<math>~x \biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr] </math>
<math>~\Rightarrow ~~~ \frac{(u-1)}{x} \frac{dx}{du}</math>	<math>~=</math>	<math>~ (A u - 1 )^{-1} \biggl[ \frac{b}{2} (A u - 1 ) - \frac{aA}{2} (u-1) \biggr] </math>
	<math>~=</math>	<math>~\frac{1 }{2(A u - 1 )} \biggl[ b (A u - 1 ) - aA (u-1) \biggr] </math>
	<math>~=</math>	<math>~ \frac{1 }{2(A u - 1 )} \biggl[ (aA - b) + A(b - a)u \biggr] \, ; </math>

and,

<math>~\frac{d^2x}{du^2}</math>	<math>~=</math>	<math>~ \biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]\frac{dx}{du} + x \frac{d}{du}\biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr] </math>
	<math>~=</math>	<math>~ x\biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]^2 + x \biggl[ -\frac{b}{2}(u-1)^{-2} + \frac{aA^2}{2} (A u - 1 )^{-2} \biggr] </math>
	<math>~=</math>	<math>~ \frac{x}{4(u-1)^2 (Au-1)^2} \biggl\{ \biggl[ b(Au-1) - aA (u - 1 ) \biggr]^2 + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr] \biggr\} </math>
<math>~\Rightarrow ~~~ \frac{(1-u)^2}{x}\frac{d^2x}{du^2}</math>	<math>~=</math>	<math>~ \frac{1}{4 (Au-1)^2} \biggl\{ \biggl[ b(Au-1) - aA (u - 1 ) \biggr]^2 + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr] \biggr\} </math>

Hence, the governing wave equation becomes,

<math>~0</math>	<math>~=</math>	<math>~2u \biggl\{ \frac{(u-1)^2}{x} \frac{d^2x}{du^2} \biggr\} + (7u-6)\biggl\{ \frac{(u-1)}{x} \frac{dx}{du} \biggl\} + 1 </math>
	<math>~=</math>	<math>~ \frac{2u}{4 (Au-1)^2} \biggl\{ \biggl[ (aA - b) + A(b - a)u \biggr]^2 + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr] \biggr\} </math>
		<math>~ + \frac{(7u-6) }{2(A u - 1 )} \biggl[ (aA - b) + A(b - a)u \biggr] + 1 </math>
	<math>~=</math>	<math>~ \frac{1}{4 (Au-1)^2} \biggl\{ 2u\biggl[ (aA - b)^2 + 2(aA - b)A(b - a)u + A^2(b - a)^2u^2 \biggr] + 2u\biggl[ 2aA^2 (u^2 - 2u + 1) -2b (A^2 u^2 - 2Au + 1 ) \biggr] </math>
		<math>~ + 2(A u - 1 )(7u-6) \biggl[ (aA - b) + A(b - a)u \biggr] + 4 (Au-1)^2 \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{4 (Au-1)^2} \biggl\{ 2u\biggl[ (aA - b)^2 + 2(aA - b)A(b - a)u + A^2(b - a)^2u^2 \biggr] + 2u\biggl[ 2A^2(a-b)u^2 + 4A(b - aA) u + 2(aA^2 -b) \biggr] </math>
		<math>~ + 2\biggl[7Au^2 - (6A+7)u +6 \biggr]\biggl[ (aA - b) + A(b - a)u \biggr] + (4A^2u^2-8Au + 4) \biggr\} </math>

If <math>~b=a</math>,

<math>~0</math>	<math>~=</math>	<math>~ 2u\biggl[ (aA - b)^2 \biggr] + 2u\biggl[ 4A(b - aA) u + 2(aA^2 -b) \biggr] </math>
		<math>~ + 2\biggl[7Au^2 - (6A+7)u +6 \biggr]\biggl[ (aA - b) \biggr] + (4A^2u^2-8Au + 4) </math>
	<math>~=</math>	<math>~ 2a^2u (A - 1)^2 + 2au [ 4A(1 - A) u + 2(A^2 -1) ] </math>
		<math>~ + 2a(A - 1) \biggl[7Au^2 - (6A+7)u +6 \biggr] + (4A^2u^2-8Au + 4) </math>
	<math>~=</math>	<math>~ 2Au^2 [4a (1 - A) + 7a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(A - 1) (6A+7) - 4A] + 4[ 3a(A-1) + 1] </math>

This should then match the "first guess" algebraic condition if we set <math>~a=1</math>. Let's see.

<math>~0</math>	<math>~=</math>	<math>~ 2Au^2 [4 (1 - A) + 7(A - 1) + 2A] + 2u [ (A - 1)^2 + 2(A^2 -1) - (A - 1) (6A+7) - 4A] + 4[ 3(A-1) + 1] </math>
	<math>~=</math>	<math>~ 2Au^2 [4 - 4A + 7A - 7 + 2A] + 2u [ (A^2 - 2A + 1) + 2A^2 -2 + (1-A ) (6A+7) -4A] + 4[ 3A-2] </math>
	<math>~=</math>	<math>~ 2Au^2 [5A - 3] + 2u [ - 3A^2 - 7A + 6 ] + 4[ 3A-2] \, . </math>

And we see that this expression does match the one derived earlier.

Going back a bit, before setting <math>~a=1</math>, we have the expression:

<math>~0</math>	<math>~=</math>	<math>~ 2Au^2 [4a (1 - A) + 7a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(A - 1) (6A+7) - 4A] + 4[ 3a(A-1) + 1] </math>
	<math>~=</math>	<math>~ 2Au^2 [ 3aA -3a + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(6A^2+A-7) - 4A] + 4[ 3a(A-1) + 1] </math>
	<math>~=</math>	<math>~ 2Au^2 [ 3a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + a( -4A^2-A+5) - 4A] + 4[ 3a(A-1) + 1] \, . </math>

Now, in order for all three expressions inside the square-bracket pairs to be zero, we need, first,

<math>~3a(A - 1) + 2A</math>	<math>~=</math>	<math>~0</math>
<math>~\Rightarrow ~~~ a</math>	<math>~=</math>	<math>~\frac{2A}{3(1-A)} \, ;</math>

and, third, by simple visual comparison with the first expression,

<math>~3a(A-1) + 1</math>	<math>~=</math>	<math>~3a(A-1) + 2A</math>
<math>~\Rightarrow A</math>	<math>~=</math>	<math>~\frac{1}{2} </math>
<math>~\Rightarrow ~~~ a</math>	<math>~=</math>	<math>~\frac{2}{3} \, ;</math>

which forces the second expression to the value,

<math>~a^2 (A - 1)^2 + a( -4A^2-A+5) - 4A</math>	<math>~=</math>	<math>~\biggl(\frac{2}{3}\biggr)^2 \biggl(-\frac{1}{2} \biggr)^2 + \frac{2}{3}\biggl[ -1-\frac{1}{2} +5 \biggr] - 2</math>
	<math>~=</math>	<math>~\frac{1}{9} + \frac{7}{3} - 2</math>
	<math>~=</math>	<math>~\frac{4}{9} \, ,</math>

which is not zero. Hence our pair of unknown parameters — <math>~a </math> and <math>~A</math> — do not simultaneously satisfy all three conditions. (Not really a surprise.)

Setup Using Lagrangian Mass Coordinate

Alternative Terms

Let's change the independent coordinate from <math>~r_0</math> to <math>~m_0</math>. In particular, the derivative operation will change as follows:

<math>~\frac{d}{dr_0}</math>

<math>~~\rightarrow~~</math>

<math>~\biggl( \frac{dm_0}{dr_0} \biggr)\frac{d}{dm_0} = \biggl( \frac{dm_0}{d\xi} \cdot \frac{d\xi}{dr_0} \biggr)\frac{d}{dm_0} \, ,</math>

so what is the expression for the leading coefficient? From above, we have,

<math>~r_0</math>	<math>~=</math>	<math>~ R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi </math>
<math>~\Rightarrow ~~~ \xi</math>	<math>~=</math>	<math>~ \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3} r_0 \, . </math>

Also, from above, we know that,

<math>~m_0</math>	<math>~=</math>	<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} </math>
<math>~\Rightarrow ~~~ \frac{dm_0}{d\xi}</math>	<math>~=</math>	<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} \biggl\{ 3\xi^2 ( 3 + \xi^2 )^{-3/2} - 3 \xi^4 ( 3 + \xi^2 )^{-5/2}\biggr\} </math>
	<math>~=</math>	<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3\xi^2 (3 + \xi^2)^{-5/2} \biggl\{ ( 3 + \xi^2 ) - \xi^2 \biggr\} </math>
	<math>~=</math>	<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} </math>
<math>~\Rightarrow ~~~ \frac{dm_0}{dr_0}</math>	<math>~=</math>	<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3} </math>
	<math>~=</math>	<math>~ \frac{M_\mathrm{tot} }{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} \, . </math>

To simplify expressions, let's borrow from an accompanying derivation and define,

<math>\tilde{C} \equiv \frac{3^2}{{\tilde\xi}^2} \biggl( 1 + \frac{ {\tilde\xi}^2}{3} \biggr) = 3 \biggl[ \frac{( 3 + {\tilde\xi}^2 )}{ {\tilde\xi}^2} \biggr] \, .</math>

Then we have,

<math>~\frac{m_0}{M_\mathrm{tot}}</math>	<math>~=</math>	<math>~ \biggl[ \frac{\tilde{C}}{ 3}\biggr]^{3 / 2} \biggl[ \frac{\xi^2}{ ( 3 + \xi^2 )} \biggr]^{3/2} </math>
<math>~\Rightarrow ~~~\biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3}</math>	<math>~=</math>	<math>~ \frac{\xi^2}{ ( 3 + \xi^2 )} </math>
<math>~\Rightarrow ~~~( 3 + \xi^2 )\biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3}</math>	<math>~=</math>	<math>~ \xi^2 </math>
<math>~\Rightarrow ~~~3 m_*</math>	<math>~=</math>	<math>~ \xi^2 (1-m_*) </math>
<math>~\Rightarrow ~~~\xi^2 </math>	<math>~=</math>	<math>~ \frac{3m_*}{(1-m_*)} \, , </math>

where,

<math>~m_* \equiv \biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3} \, .</math>

In summary:

<math>~ \frac{\xi^2}{ ( 3 + \xi^2 )} = m_* \, ; </math>

while,

<math>~ \frac{ {\tilde\xi}^2}{ ( 3 + {\tilde\xi}^2 )} = \frac{3}{\tilde{C}} \, ; </math>

<math>~r_0</math>	<math>~=</math>	<math>~ R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi = R_* \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggr[ \frac{3m_*}{ (1-m_*) }\biggr]^{1 / 2} \, ; </math>
<math>~\frac{g_0\rho_0}{P_0} </math>	<math>~=</math>	<math>~ \frac{6}{R_*} \biggl[ \frac{ {\tilde\xi}^2 }{ (3 + {\tilde\xi}^2) }\biggr]^{9} \frac{\xi}{ ( 3 + \xi^2 )} = \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} \frac{m_*}{ \xi } = \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \, ; </math>
<math>~\frac{g_0 }{r_0} </math>	<math>~=</math>	<math>~ \frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{ {\tilde\xi}^2 }{ (3 + {\tilde\xi}^2)}\biggr]^{15/2} \frac{1}{\xi^3} \biggl[ \frac{ \xi^2 }{ ( 3 + \xi^2 ) }\biggr]^{3/2} = \frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \, ; </math>
<math>~\frac{\rho_0}{\gamma_g P_0} </math>	<math>~=</math>	<math>~ \frac{6R_* }{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \, . </math>

So, the wave equation may be written as,

<math>~0</math>	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x </math>
	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \biggl\{ \frac{4}{R_*} \biggl( \frac{ 3}{ \tilde{C} }\biggr)^{3} \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2} - \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr\} \frac{dx}{dr_0} </math>
		<math>~ + \frac{6R_* }{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{ \omega^2 + (4 - 3\gamma_\mathrm{g})\frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x </math>
	<math>~=</math>	<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_*} \biggl( \frac{ 3}{ \tilde{C} }\biggr)^{3} \biggl\{ 4 - 6\biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{6} m_* \biggr\} \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}\frac{dx}{dr_0} </math>
		<math>~ + \frac{6(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot \frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{\sigma^2 + (1-m_*)^{3 / 2} \biggr\} x </math>
	<math>~=</math>	<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl\{ R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2} + R_* \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}\frac{dx}{dr_0} </math>
		<math>~ + \frac{6(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math>
	<math>~=</math>	<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2} R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2} + R_* \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \frac{dx}{dr_0} </math>
		<math>~ + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} \, , </math>

where,

<math>~\sigma^2 \equiv (4 - 3\gamma_\mathrm{g})^{-1} \frac{R_*^3}{GM_\mathrm{tot}} \biggl[ \frac{ \tilde{C} }{3 } \biggr]^{15/2} \omega^2 \, .</math>

Now, let's look at the differential operators, after defining.

<math>~c_0 \equiv 3^{1 / 2} R_* \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} ~~~~\Rightarrow ~~~~R_* = c_0 3^{-1 / 2} \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} \, .</math>

We find,

<math>~dr_0</math>	<math>~=</math>	<math>~ c_0 ~d[ m_*^{1 / 2} (1-m_*)^{-1 / 2} ] </math>
	<math>~=</math>	<math>~ c_0 ~\biggl[\frac{1}{2} ~m_*^{-1 / 2}( 1 - m_*)^{-1 / 2} + \frac{1}{2} ~m_*^{1 / 2} (1 - m_*)^{-3 / 2} \biggr] dm_* </math>
	<math>~=</math>	<math>~ \frac{c_0}{2} ~m_*^{-1 / 2}( 1 - m_*)^{-3 / 2}~ dm_* </math>
<math>~\frac{d}{dr_0}</math>	<math>~=</math>	<math>~ \frac{2}{c_0} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} </math>
<math>~\Rightarrow ~~~ R_*\frac{dx}{dr_0}</math>	<math>~=</math>	<math>~ \frac{2}{3^{1 / 2}}\biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \, . </math>

Also,

<math>~\frac{d^2}{dr_0^2}</math>	<math>~=</math>	<math>~ \biggl( \frac{2}{c_0} \biggr)^{2}~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} \biggl[ m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} \biggr] </math>
	<math>~=</math>	<math>~ \biggl( \frac{2}{c_0} \biggr)^{2}~m_* ( 1 - m_*)^{3 }~ \frac{d^2}{dm_*^2} +\biggl( \frac{2}{c_0} \biggr)^{2}~m_*^{1 / 2}( 1 - m_*)^{3 / 2} \biggl[ \frac{1}{2} m_*^{-1 / 2}( 1 - m_*)^{3 / 2} - \frac{3}{2} m_*^{1 / 2}( 1 - m_*)^{1 / 2}~ \biggr] ~ \frac{d}{dm_*} </math>
	<math>~=</math>	<math>~ \biggl( \frac{2}{c_0} \biggr)^{2}~m_* ( 1 - m_*)^{3 }~ \frac{d^2}{dm_*^2} +\frac{1}{2} \biggl( \frac{2}{c_0} \biggr)^{2}~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{d}{dm_*} </math>
<math>~\Rightarrow ~~~ R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2}</math>	<math>~=</math>	<math>~ \biggl[\frac{2^2}{3} \biggl(\frac{ \tilde{C} }{3} \biggr)^{-3} \biggr] \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr] </math>

So, the wave equation becomes,

<math>~0</math>	<math>~=</math>	<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2} \biggl[\frac{2^2}{3} \biggl(\frac{ \tilde{C} }{3} \biggr)^{-3} \biggr] \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr] </math>
		<math>~ + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \biggl[ \frac{2}{3^{1 / 2}}\biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \biggr] + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math>
	<math>~=</math>	<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2} \biggl[\frac{2^2}{3} \biggr] \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr] </math>
		<math>~ + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \biggl[ \frac{2}{3^{1 / 2}} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \biggr] + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math>
	<math>~=</math>	<math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} + ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} </math>
		<math>~ + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^2 \frac{dx}{dm_*} + \frac{9(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}\biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math>
	<math>~=</math>	<math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} </math>
		<math>~ + \biggl[ 5 - 4m_* - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^2 \frac{dx}{dm_*} + \frac{9(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}\biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math>
	<math>~=</math>	<math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} + (5 - \mathcal{A} m_*) (1-m_*)^2 \frac{dx}{dm_*} + \mathcal{B} \biggl[ \frac{\sigma^2}{(1-m_*)^{1 / 2}} + (1-m_*) \biggr] x \biggr\} \, , </math>

where,

<math>~\mathcal{A}</math>	<math>~\equiv</math>	<math>~4 + 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} \, ,</math>
<math>~\mathcal{B}</math>	<math>~\equiv</math>	<math>~\frac{3^{5/2}(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \, .</math>

Try Again

This time, let's adopt the notation used in a related chapter in our Ramblings appendix. Specifically, the parametric relationship between <math>~m_\xi</math> and <math>~r_\xi</math> in pressure-truncated, <math>~n=5</math> polytropes is,

<math>~m_\xi \equiv \frac{m_0}{ M_\mathrm{tot} } = \frac{M_r(\xi)}{M_\mathrm{tot}}</math>	<math>~=</math>	<math>~ \biggl(\frac{\xi}{\tilde\xi}\biggr)^3 \biggl(3 + \xi^2 \biggr)^{-3/2} \biggl(3 + {\tilde\xi}^2 \biggr)^{3/2} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]^{3 / 2}\biggl[ \frac{( 3+\xi^2)}{ {\xi}^2} \biggr]^{- 3 / 2} \, ,</math>
<math>~r_\xi \equiv \frac{r_0}{R_\mathrm{norm}} = \biggl(\frac{\xi}{\tilde\xi} \biggr) \frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math>	<math>~=</math>	<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3^7}\biggr]^{1/2} \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]^{3} \xi \, . </math>

And we are in the fortunate situation of being able to eliminate <math>~\xi</math> to obtain the direct relation,

<math>~ r_\xi (m_\xi) </math>

<math>~=</math>

<math>~\tilde{r}_\mathrm{edge} \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} \, , </math>

where,

<math>~\tilde{C}</math>	<math>~\equiv</math>	<math>~ \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr) = 3 \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr] \, , </math>
<math>~\tilde{r}_\mathrm{edge}</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} {\tilde\xi}^{-6} \biggl(1+\frac{\tilde\xi^2}{3}\biggr)^3 = \biggl[ \frac{\pi}{2^3\cdot 3^7}\biggr]^{1 / 2} \biggl[ \frac{\tilde{C}}{ 3} \biggr]^{3} \, . </math>

If we furthermore define,

<math>m_* \equiv \frac{3}{\tilde{C}} \cdot m_\xi^{2 / 3} \, ,</math>

then,

<math>~ r_\xi (m_*) </math>

<math>~=</math>

<math>~ 3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl[\frac{m_*}{1-m_*}\biggr]^{1/2} \, . </math>

Hence,

<math>~ \frac{dr_0}{R_\mathrm{norm}} = dr_\xi </math>	<math>~=</math>	<math>~3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl\{ \frac{1}{2} (1-m_*)^{- 1 / 2} m_*^{-1 / 2} + \frac{1}{2}m_*^{1 / 2}(1-m_*)^{-3 / 2} \biggr\} dm_* </math>
	<math>~=</math>	<math>~ \biggl( \frac{3^{1 / 2}}{2} \biggr) \tilde{r}_\mathrm{edge} m_*^{-1 / 2} (1-m_*)^{-3 / 2} dm_* </math>
<math>\Rightarrow ~~~ R_\mathrm{norm} \cdot \frac{d}{dr_0} </math>	<math>~=</math>	<math>~ \frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*} \, . </math>

We therefore also have,

<math>~ R^2_\mathrm{norm} \cdot \frac{d^2}{dr_0^2} </math>	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2^2}{3} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*}\biggl[ m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*}\biggr] </math>
	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2^2}{3} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \biggl\{ \biggl[ m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d^2}{dm_*^2}\biggr] + \biggl[ \frac{1}{2} m_*^{-1 / 2} (1-m_*)^{3 / 2} + \frac{3}{2}m_*^{1 / 2} (1-m_*)^{1 / 2}\biggr] \frac{d}{dm_*} \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ \biggl[ 2m_* (1-m_*)^{3} \frac{d^2}{dm_*^2}\biggr] + \biggl[ (1-m_*)^{3 } + 3m_* (1-m_*)^{2}\biggr] \frac{d}{dm_*} \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{d}{dm_*} \biggr\} \, . </math>

So the wave equation may be written,

<math>~0</math>	<math>~=</math>	<math>~ R_\mathrm{norm}^2 \cdot \frac{d^2x}{dr_0^2} + \biggl[\frac{4R_\mathrm{norm}}{r_0} - \biggl(\frac{g_0 \rho_0 R_\mathrm{norm}}{P_0}\biggr) \biggr] R_\mathrm{norm} \cdot \frac{dx}{dr_0} + \biggl(\frac{\rho_0 R_\mathrm{norm}}{\gamma_\mathrm{g} P_0} \biggr)\biggl[R_\mathrm{norm} \omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0 R_\mathrm{norm}}{r_0} \biggr] x </math>
	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\} </math>
		<math>~ +\frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) \biggl\{ \frac{4}{r_\xi} - \biggl[\frac{6R_\mathrm{norm}}{R_*} \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr] \biggr\} m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{dx}{dm_*} </math>
		<math>~ + \frac{6R_* R_\mathrm{norm}}{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{ R_\mathrm{norm} \omega^2 + (4 - 3\gamma_\mathrm{g}) \frac{GM_\mathrm{tot} R_\mathrm{norm}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x \, . </math>

Keeping in mind that,

<math>~\frac{R_*}{R_\mathrm{norm}} = \biggl[ \frac{\pi}{2^3 \cdot 3^7} \biggr]^{1 / 2} = {\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \, ,</math>

we therefore have,

<math>~0</math>	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\} </math>
		<math>~ +\frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) \biggl\{ 4 \biggl[3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl[\frac{m_*}{1-m_*}\biggr]^{1/2} \biggr]^{-1} - 6 \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{9} \biggl[{\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \biggr]^{-1} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr\} m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{dx}{dm_*} </math>
		<math>~ + 6 \biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[{\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \biggr]^{-2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{ \biggl[ \frac{R_*^3}{\gamma_g GM_\mathrm{tot} } \biggr] \omega^2 + \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x </math>
	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\} </math>
		<math>~ +\frac{1}{ \tilde{r}_\mathrm{edge}^2} \biggl( \frac{2^3}{3} \biggr) \biggl[ 1 - \frac{3}{2} \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^{2} \frac{dx}{dm_*} + \frac{6}{ {\tilde{r}}_\mathrm{edge}^2 } \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x </math>
	<math>~=</math>	<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + \biggl[ 5 - 6 \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* + 2m_* \biggr] (1-m_*)^{2} \frac{dx}{dm_*} + 3^{5 / 2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \frac{\sigma^2 }{(1-m_*)^{1 / 2}} + (1-m_*) \biggr] x \biggr\} \, , </math>

where, as before,

<math>\sigma^2 \equiv \biggl( \frac{ \tilde{C} }{3 } \biggr)^{15/2} \biggl[ \frac{R_*^3}{(4 - 3\gamma_g) GM_\mathrm{tot} } \biggr] \omega^2 \, .</math>

n = 3 Polytrope

Here we perform a numerical integration of the governing LAWE for <math>~n=3</math> polytropes. We can directly compare our results with Schwarzschild's (1941) published work on "Overtone Pulsations for the Standard [Stellar] Model."

Drawing from our above discussion, the LAWE for any polytrope of index, <math>~n</math>, may be written as,

<math>~0 </math>	<math>~=</math>	<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>
	<math>~=</math>	<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi} \biggr)\biggr] \frac{dx}{d\xi} + \frac{(n+1)}{\theta} \biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi } \biggl(- \frac{d\theta}{d\xi} \biggr) \biggr] x </math>

where,

<math>~\sigma_c^2</math>

<math>~\equiv</math>

<math>~\frac{3\omega^2}{2\pi G\rho_c} \, .</math>

It can be shown straightforwardly that this matches the LAWE used by Schwarzschild (1941), if <math>~n</math> is set to 3. But let's postpone making this substitution until we formulate a general approach to integrating this equation from the center of the configuration, outward. Following a parallel discussion, we begin by multiplying the LAWE through by <math>~(\xi\theta)</math>, obtaining a 2^nd-order ODE that is relevant at every individual coordinate location, <math>~\xi_i</math>, namely,

<math>~\theta_i {x_i}</math>

<math>~=</math>

<math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \frac{x_i'}{\xi_i} - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>

Now, using the general finite-difference approach described separately, we make the substitutions,

<math>~x_i'</math>

<math>~\approx</math>

<math>~ \frac{x_+ - x_-}{2 \Delta_\xi} \, ; </math>

and,

<math>~ x_i </math>

<math>~\approx</math>

<math>~\frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \, ,</math>

which will provide an approximate expression for <math>~x_+ \equiv x_{i+1}</math>, given the values of <math>~x_- \equiv x_{i-1}</math> and <math>~x_i</math>. Specifically, if the center of the configuration is denoted by the grid index, <math>~i=1</math>, then for zones, <math>~i = 3 \rightarrow N</math>,

<math>~\theta_i \biggl[ \frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \biggr]</math>	<math>~=</math>	<math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ - x_-}{2 \xi_i \Delta_\xi} \biggr] - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
<math>~\Rightarrow ~~~ \theta_i \biggl[ \frac{x_+ }{\Delta_\xi^2} \biggr] + \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ }{2 \xi_i\Delta_\xi} \biggr]</math>	<math>~=</math>	<math>~ -\theta_i \biggl[ \frac{- 2x_i + x_-}{\Delta_\xi^2} \biggr] - \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{- x_-}{2 \xi_i \Delta_\xi} \biggr] - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
<math>~\Rightarrow ~~~ x_+ \biggl[2\theta_i +\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i\biggr] </math>	<math>~=</math>	<math>~ x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr] + x_i\biggl\{4\theta_i - 2\Delta_\xi^2(n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr] + x_i\biggl\{4\theta_i - \frac{\Delta_\xi^2(n+1)}{3}\biggl[ \frac{\sigma_c^2}{\gamma_g} - 2\alpha \biggl(- \frac{3\theta^'}{\xi}\biggr)_i\biggr] \biggr\} \, .</math>

In order to kick-start the integration, at the center of the configuration <math>~(\xi_1 = 0)</math>, we will set the eigenfunction value to <math>~x_1 = 1</math>; and we will use the assumed symmetry condition, <math>~x_1' = 0 ~~\Rightarrow ~~ x_- = x_+</math>, in order to determine the value of the eigenfunction at the first grid location off center <math>~(\xi_2 = \Delta)</math>. That is, for <math>~i = 1</math>, the discretized LAWE gives,

<math>~ x_+ </math>

<math>~=</math>

<math>~ x_i \biggl\{ 1 -\frac{\Delta_\xi^2 (n+1)}{2\theta_i}\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] \biggr\} \, .</math>

Given that the power-series representation of the Lane-Emden function is,

<math>~\theta</math>

<math>~=</math>

<math>~ 1 - \frac{\xi^2}{6} + \frac{n}{120} \xi^4 - \frac{n}{378} \biggl( \frac{n}{5} - \frac{1}{8} \biggr) \xi^6 + \biggl[ \frac{n(122n^2 -183n + 70)}{3265920} \biggr] \xi^8 + \cdots </math>

we know that in this individual case <math>~(i=1)</math> — that is, for <math>~\xi = 0</math> — <math>~\theta = 1</math> and <math>~(-\theta')/\xi = \tfrac{1}{3}</math> for all values of the polytropic index. Hence, for <math>~i=1</math>, we can use the expression,

<math>~ x_2 </math>

<math>~=</math>

<math>~ x_1 [ 1 - \tfrac{1}{12} \Delta_\xi^2 (n+1) \mathfrak{F} ] \, ,</math>

where,

<math>~ \mathfrak{F} </math>

<math>~\equiv</math>

<math>~ \biggl[ \frac{\sigma_c^2}{\gamma_g} - 2\alpha\biggr]\, .</math>

Related Discussions

• In an accompanying Chapter within our "Ramblings" Appendix, we have played with the adiabatic wave equation for polytropes, examining its form when the primary perturbation variable is an enthalpy-like quantity, rather than the radial displacement of a spherical mass shell. This was done in an effort to mimic the approach that has been taken in studies of the stability of Papaloizou-Pringle tori.

• <math>~n=3</math> … M. Schwarzschild (1941, ApJ, 94, 245), Overtone Pulsations of the Standard Model: This work is referenced in §38.3 of [KW94]. It contains an analysis of the radial modes of oscillation of <math>~n=3</math> polytropes, assuming various values of the adiabatic exponent.

• <math>~n=2</math> … C. Prasad & H. S. Gurm (1961, MNRAS, 122, 409), Radial Pulsations of the Polytrope, n = 2

• <math>~n=\tfrac{3}{2}</math> … D. Lucas (1953, Bul. Soc. Roy. Sci. Liege, 25, 585) … Citation obtained from the Prasad & Gurm (1961) article.

• <math>~n=1</math> … L. D. Chatterji (1951, Proc. Nat. Inst. Sci. [India], 17, 467) … Citation obtained from the Prasad & Gurm (1961) article.

• Composite Polytropes … M. Singh (1968, MNRAS, 140, 235-240), Effect of Central Condensation on the Pulsation Characteristics

• Summary of Known Analytic Solutions … R. Stothers (1981, MNRAS, 197, 351-361), Analytic Solutions of the Radial Pulsation Equation for Rotating and Magnetic Star Models

• Interesting Composite! … C. Prasad (1948, MNRAS, 108, 414-416), Radial Oscillations of a Particular Stellar Model

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation