User:Tohline/Apps/ImamuraHadleyCollaboration

Characteristics of Unstable Eigenvectors in Self-Gravitating Tori

In what follows, we will draw heavily from three publications: (1) J. E. Tohline & I. Hachisu (1990, ApJ, 361, 394-407) — hereafter, TH90 — (2) J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247-267) — hereafter, WTH94 — and (3) K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1) — hereafter, HI11.

Background

Imamura & Hadley Collaboration

Based especially on the analysis provided in Paper I and Paper II of the Imamura & Hadley collaboration, the eigenvectors that have drawn our attention thus far can be categorized as J-modes (as discussed, for example, in §3.2.1, Table 1 & Figure 2 of Paper II) or I-modes. Our initial attempts to construct fits to these eigenvectors empirically have been described in an separate chapter. We begin, here, a more quantitative analysis of the structure of these unstable eigenvectors by borrowing from a subsection of that chapter a table of equilibrium parameter values for the typical P- and E-mode models described in Table 2 of Paper II.

Table 1:  P- and E-mode Model Parameters Highlighted in Paper II K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222)
Extracted from Table 2 or Table 4 of Paper II						Deduced Here			Extracted from Fig. 3 or Fig. 4 of Paper II
Name	<math>~M_*/M_d</math>	<math>~(n, q)</math>†	<math>~R_-/R_+</math>	<math>~r_\mathrm{outer} \equiv \frac{R_+}{R_\mathrm{max}}</math>	<math>~R_\mathrm{max}</math>	<math>~R_+</math>	<math>~\epsilon \equiv \frac{R_\mathrm{max}-R_-}{R_\mathrm{max}}</math>	<math>~r_- \equiv \frac{R_-}{R_\mathrm{max}}</math>	Eigenfunction
E1	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.101</math>	<math>~5.52</math>	<math>~0.00613</math>	<math>~0.0338</math>	<math>~0.442</math>	<math>~0.558</math>
E2	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.202</math>	<math>~2.99</math>	<math>~0.0229</math>	<math>~0.0685</math>	<math>~0396</math>	<math>~0.604</math>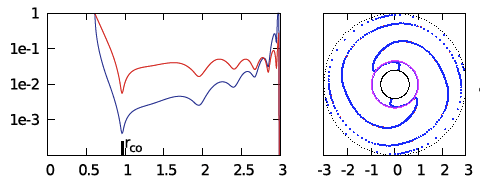
E3	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.402</math>	<math>~1.74</math>	<math>~0.159</math>	<math>~0.277</math>	<math>~0.301</math>	<math>~0.699</math>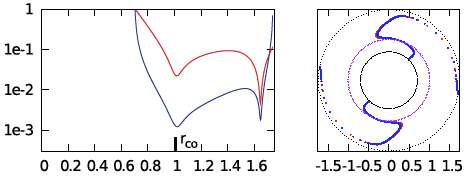
P1	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.452</math>	<math>~1.60</math>	<math>~0.254</math>	<math>~0.406</math>	<math>~0.277</math>	<math>~0.723</math>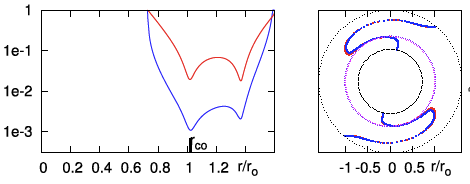
P2	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.500</math>	<math>~1.49</math>	<math>~0.403</math>	<math>~0.600</math>	<math>~0.255</math>	<math>~0.745</math>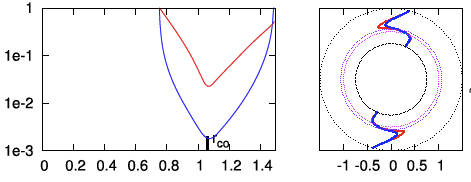
P3	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.600</math>	<math>~1.33</math>	<math>~1.09</math>	<math>~1.450</math>	<math>~0.202</math>	<math>~0.798</math>
P4	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.700</math>	<math>~1.21</math>	<math>~3.37</math>	<math>~4.078</math>	<math>~0.153</math>	<math>~0.847</math>
†In all three papers from the Imamura & Hadley collaboration, <math>~q = 2</math> means, "uniform specific angular momentum."

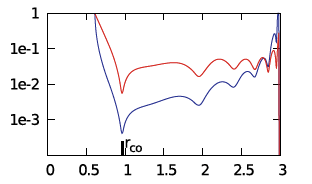
We ask, first, "Can we understand why the radial eigenfunction of, for example, model E2 — re-displayed here, on the right — exhibits a series of sharp dips whose spacing gets progressively smaller and smaller as the outer edge of the torus is approached?"

See Also

• Imamura & Hadley collaboration:
  • Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks.   I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
  • Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks.   II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
  • Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks.   III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation