Analyzing Azimuthal Distortions

Adopted Notation

We will adopt the notation of J. E. Tohline & I. Hachisu (1988, ApJ, 361, 394). Specifically, drawing on their equation (2) but ignoring variations in the vertical coordinate, the mass density is given by the expression,

<math>~\rho_0 \biggl[ 1 + f(\varpi)e^{-i(\omega t - m\phi)} \biggr] \, ,</math>

where it is understood that <math>~\rho_0</math>, which defines the structure of the initial axisymmetric equilibrium configuration, is generally a function of the cylindrical radial coordinate, <math>~\varpi</math>.

Using the subscript, <math>~m</math>, to identify the time-invariant coefficients and functions that characterize the intrinsic eigenvector of each azimuthal eigen-mode, and acknowledging that the associated eigenfrequency will in general be imaginary, that is,

<math>~\omega_m</math>

<math>~\omega_R + i\omega_I \, ,</math>

we expect each unstable mode to display the following behavior:

<math>~\biggl[ \frac{\rho}{\rho_0} - 1 \biggr]</math>	<math>~=</math>	<math>~f_m(\varpi)e^{-i[\omega_R t + i \omega_I t - m\phi_m(\varpi)]} </math>
	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-im\phi_m(\varpi)}\biggr\} e^{-i\omega_R t } \cdot e^{\omega_I t} </math>
	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-i[\omega_R t + m\phi_m(\varpi)]} \biggr\} e^{\omega_I t} \, .</math>

Adopting Kojima's (1986) notation, that is, defining,

<math>~y_1 \equiv \frac{\omega_R}{\Omega_0} - m</math>

and

<math>~y_2 \equiv \frac{\omega_I}{\Omega_0} \, ,</math>

the eigenvector's behavior can furthermore be described by the expression,

<math>~\biggl[ \frac{\rho}{\rho_0} - 1 \biggr]</math>	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-i[(y_1+m) (\Omega_0 t) + m\phi_m(\varpi)]} \biggr\} e^{y_2 (\Omega_0 t)} </math>
	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-im[(y_1/m+1) (\Omega_0 t) + \phi_m(\varpi)]} \biggr\} e^{y_2 (\Omega_0 t)} \, .</math>

Note that, as viewed from a frame of reference that is rotating with the mode pattern frequency,

<math>\Omega_p \equiv \frac{\omega_R}{m} = \Omega_0\biggl(\frac{y_1}{m}+1\biggr) \, ,</math>

we should find an eigenvector of the form,

<math>~\biggl[ \frac{\rho}{\rho_0} - 1 \biggr]_\mathrm{rot} \equiv \biggl[ \frac{\rho}{\rho_0} - 1 \biggr]e^{im\Omega_p t}</math>

<math>~\biggl\{ f_m(\varpi)e^{-im[\phi_m(\varpi)]} \biggr\} e^{y_2 (\Omega_0 t)} \, ,</math>

whose relative amplitude — with a radial structure as specified inside the curly braces — is undergoing a uniform exponential growth but is otherwise unchanging.

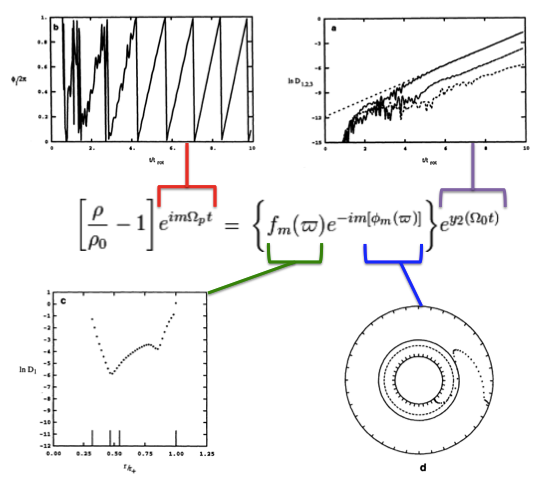
Figure 1 illustrates how the behavior of each factor in this expression can reveal itself during a numerical simulation that follows the time-evolutionary development of an unstable, nonaxisymmetric eigenmode. The initial model for this depicted evolution was a zero-mass — that is, a Papaloizou-Pringle like torus — with <math>~n = 3</math> and <math>~q = 2</math>. The top-left panel shows how the phase angle, <math>~\phi_2/(2\pi)</math> for an unstable, <math>~m=2</math> eigenmode varies with time, <math>~t/\tau_\mathrm{rot}</math>, where the rotation period at the density maximum,

<math>~t_\mathrm{rot} \equiv \frac{2\pi}{\Omega_0} \, .</math>

Figure 1

Four panels extracted^† from figure 2, p. 252 of J. W. Woodward, J. E. Tohline & I. Hachisu (1994)

"The Stability of Thick, Self-gravitating Disks in Protostellar Systems"

ApJ, vol. 420, pp. 247-267 © American Astronomical Society

^†As displayed here, the layout of figure panels (a, b, c, d) has been modified from the original publication layout; otherwise, each panel is unmodified.

Empirical Construction of Eigenvector

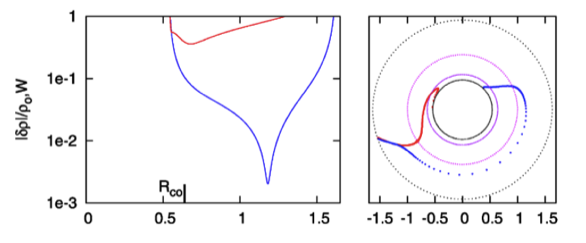
Figure 2

Panel pair extracted^† without modification from the top-most segment of Figure 13, p. 12 of K. Hadley & J. N. Imamura (2011a)

"Nonaxisymmetric Instabilities of Self-Gravitating Disks. I Toroids"

Astrophysics and Space Science, 334, 1 - 26 © Springer Science+Business Media B.V.

^†This pair of plots also appears, by itself, as Figure 6 on p. 12 of K. Hadley & J. N. Imamura (2011a).

Figure 3: Our Empirically Constructed Eigenvector

First, specify a "midway" radial location, <math>~r_- < r_\mathrm{mid} < r_+ \, ,</math> at which the density fluctuation is smallest. Then define a function of the form,

<math>~f(\varpi)</math>	<math>~=</math>	<math>~\tanh^{-1}\biggl[1 - 2 \biggl( \frac{\varpi - r_-}{r_\mathrm{mid}-r_-} \biggr) \biggr]</math>	for	<math>r_- < \varpi < r_\mathrm{mid} \, ;</math>
and
<math>~f(\varpi)</math>	<math>~=</math>	<math>~\tanh^{-1}\biggl[1 - 2 \biggl( \frac{\varpi - r_+}{r_\mathrm{mid}-r_+} \biggr) \biggr]</math>	for	<math>r_\mathrm{mid} < \varpi < r_+ \, .</math>

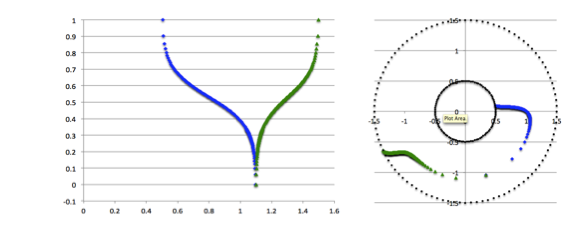
As shown by the following figure montage, this <math>~f(\varpi)</math> function very closely resembles the one generated by Imamura via a linear stability analysis.

PRACTICAL IMPLEMENTATION: At the two limits, <math>~\varpi = r_-</math> and <math>~\varpi = r_+</math>, the function, <math>~f(\varpi) \rightarrow +\infty</math>; while, at the limit, <math>~\varpi = r_\mathrm{mid}</math>, the function, <math>~f(\varpi) \rightarrow -\infty</math>. In practice we stay half of a radial zone away from these three limiting radial boundaries, so that the maximum and minimum values of <math>~f(\varpi)</math> are finite; then we strategically employ the finite values of the function at these near-boundary limits to rescale the function such that, in the plot shown below, it lies between zero (minimum amplitude) and unity (maximum amplitude).

Now, the following general relation holds:

<math>~\frac{1}{2} \ln\biggl( \frac{1+x}{1-x} \biggr) </math>

for

Hence, for the innermost region of the toroidal configuration, we can set,

<math>~x</math>	<math>~=</math>	<math>~1 - 2 \biggl( \frac{\varpi - r_-}{r_\mathrm{mid}-r_-} \biggr) </math>
<math>~\Rightarrow ~~~~ \frac{1+x}{1-x}</math>	<math>~=</math>	<math> ~\biggl[2 - 2 \biggl( \frac{\varpi - r_-}{r_\mathrm{mid}-r_-} \biggr)\biggr] \biggl[2 \biggl( \frac{\varpi - r_-}{r_\mathrm{mid}-r_-} \biggr)\biggr]^{-1} </math>
	<math>~=</math>	<math> ~[(r_\mathrm{mid}-r_-) - ( \varpi - r_-)] [(\varpi - r_-)]^{-1} </math>
	<math>~=</math>	<math> ~\frac{r_\mathrm{mid} - \varpi}{\varpi - r_-} \, . </math>

Therefore we can write,

<math>~f(\varpi)</math>

<math>~\frac{1}{2} \ln\biggl( \frac{r_\mathrm{mid} - \varpi}{\varpi - r_-} \biggr) </math>

for

and, similarly, we find,

<math>~f(\varpi)</math>

<math>~\frac{1}{2} \ln\biggl( \frac{r_\mathrm{mid} - \varpi}{\varpi - r_+} \biggr) </math>

for

<math>r_\mathrm{mid} < \varpi < r_+ \, .</math>

Now let's work on the phase function, <math>~\phi_m(\varpi)</math>, for the specific case, <math>~m=1</math>.

<math>~D(\varpi)</math>	<math>~=</math>	<math>~\frac{f(\varpi) - f_\mathrm{min}}{f_\mathrm{max} - f_\mathrm{min}} \, ;</math>
<math>~\phi(\varpi) + \phi_0</math>	<math>~=</math>	<math>~\biggl\{\tan^{-1}[8\cdot D(\varpi)] - \frac{\pi}{2} \biggr\} + \frac{\pi}{10} \, .</math>

Now, for the specific case being graphically illustrated here, <math>~f_\mathrm{min} = -2.99448</math> and <math>~f_\mathrm{max} = 2.64665</math>. Hence,

<math>~\phi(\varpi) + \frac{\pi}{2} </math>	<math>~=</math>	<math>~\tan^{-1}\biggl[8\cdot \biggl(\frac{f(\varpi) - f_\mathrm{min}}{f_\mathrm{max} - f_\mathrm{min}} \biggr)\biggr] </math>
	<math>~=</math>	<math>~\tan^{-1}[a\cdot f(\varpi) + b] \, , </math>

where, <math>~a = 1.41816</math> and <math>~b = 4.24664</math>.

User:Tohline/Appendix/Ramblings/Azimuthal Distortions

Contents

Analyzing Azimuthal Distortions

Adopted Notation

Empirical Construction of Eigenvector

See Also

Navigation menu

Search