Virial Equilibrium of Adiabatic Spheres

Review

In an introductory discussion of the virial equilibrium structure of spherically symmetric configurations — see especially the section titled, Energy Extrema — we deduced that a system's equilibrium radius, <math>~R_\mathrm{eq}</math>, measured relative to a reference length scale, <math>~R_0</math>, i.e., the dimensionless equilibrium radius,

<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_0} \, ,</math>

is given by the root(s) of the following equation:

<math> 2C \chi^{-2} + ~ (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, , </math>

where the definitions of the various coefficients are,

<math>~A</math>	<math>~\equiv</math>	<math>\frac{3}{5} \frac{GM_\mathrm{tot} ^2}{R_0} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \, ,</math>
<math>~B</math>	<math>~\equiv</math>	<math> \frac{K M_\mathrm{tot} }{(\gamma_g-1)} \biggl( \frac{3M_\mathrm{tot} }{4\pi R_0^3} \biggr)^{\gamma_g - 1} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} = \frac{\bar{c_s}^2 M_\mathrm{tot} }{(\gamma_g - 1)} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \, , </math>
<math>~B_I</math>	<math>~\equiv</math>	<math> 3c_s^2 M_\mathrm{tot} \, , </math>
<math>~C</math>	<math>~\equiv</math>	<math> \frac{5J^2}{4M_\mathrm{tot} R_0^2} \cdot \frac{\mathfrak{f}_T}{\mathfrak{f}_M} \, , </math>
<math>~D</math>	<math>~\equiv</math>	<math> \frac{4}{3} \pi R_0^3 P_e \, . </math>

Once the pressure exerted by the external medium (<math>~P_e</math>), and the configuration's mass (<math>~M_\mathrm{tot}</math>), angular momentum (<math>~J</math>), and specific entropy (via <math>~K</math>) — or, in the isothermal case, sound speed (<math>~c_s</math>) — have been specified, the values of all of the coefficients are known and <math>~\chi_\mathrm{eq}</math> can be determined.

Isolated, Nonrotating Configuration

For a nonrotating configuration <math>(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>(D=P_e = 0)</math>, the statement of virial equilibrium is,

<math> (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} = 0 \, . </math>

Adiabatic Evolutions

For adiabatic configurations <math>(\delta_{1\gamma_g} = 0)</math>, one equilibrium state exists for each value of <math>\gamma_g</math> and it occurs where,

<math> 3(\gamma_g-1) B\chi^{3 -3\gamma_g} = A\chi^{-1} \, , </math>

that is, where,

<math> R_\mathrm{eq} = R_0 \chi_\mathrm{eq} = \biggl[ \frac{3(\gamma_g-1) B}{A} \cdot R_0^{(3\gamma_g-4)} \biggr]^{1/(3\gamma_g-4)} = \biggl[ 5\biggl( \frac{3}{4\pi} \biggr)^{\gamma_g-1} \cdot \frac{KM^{(\gamma_g-2)}}{G} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_W} \biggr]^{1/(3\gamma_g-4)} \, . </math>

Accordingly, the equilibrium mass-radius relationship for adiabatic configurations of a given specific entropy is,

<math> M^{(\gamma_g - 2)} \propto R_\mathrm{eq}^{(3\gamma_g -4)} \, . </math>

Notice that, for <math>\gamma_g=2</math>, the equilibrium radius depends only on the specific entropy of the gas and is independent of the configuration's mass. Conversely, notice that, for <math>\gamma_g = 4/3</math>, the mass of the configuration is independent of the radius. For <math>\gamma_g</math> > <math> 2</math> or <math>\gamma_g </math>< <math>4/3</math>, configurations with larger mass (but the same specific entropy) have larger equilibrium radii. However, for <math>\gamma_g</math> in the range, <math>2</math> > <math>\gamma_g </math> > <math>4/3</math>, configurations with larger mass have smaller equilibrium radii. Note that the result obtained for the isothermal configuration could have been obtained by setting <math>\gamma_g = 1</math> in this adiabatic solution, because <math>K = c_s^2</math> when <math>\gamma_g = 1</math>.

It is also instructive to write the coefficient <math>B</math> in terms of the average sound speed as defined above. In this case,

<math> R_\mathrm{eq} = R_0 \biggl[ \frac{GM}{5 \bar{c_s}^2 R_0} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A} \biggr]^{1/(4- 3\gamma_g)} \, , </math>

so the equilibrium radius of an isolated, nonrotating, uniform density, adiabatic sphere is,

<math> R_\mathrm{eq} = R_0 = \frac{GM}{5 \bar{c_s}^2 }\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A} \, . </math>

Role of Structural Form Factors

When employing a virial analysis to determine the radius of an equilibrium configuration, it is customary to set the structural form factors, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math>, to unity and accept that the expression derived for <math>~R_\mathrm{eq}</math> is an estimate of the configuration's radius that is good to within a factor of order unity. As has been demonstrated in our related discussion of the equilibrium of uniform-density spheres, these form factors can be evaluated if/when the internal structural profile of an equilibrium configuration is known from a complementary detailed force-balance analysis. In the case being discussed here of isolated, spherical polytropes, solutions to the,

Lane-Emden Equation

<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>

can provide the desired internal structural information.

For example, after discussing several analytically expressible solutions to the Lane-Emden equation, Chandrasekhar [C67] — see p. 98, Equation (72) — shows that the general mass-radius relationship for isolated spherical polytropes is,

<math> ~\frac{(n+1)K}{(4\pi)^{1/n}} \biggl[ - \xi^{(n+1)/(n-1)} \frac{d\Theta_H}{d\xi} \biggr]^{(n-1)/n}_{\xi=\xi_1} \, , </math>

which we choose to rewrite as,

<math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R^{(3-n)}</math>	<math>~=</math>	<math> ~(n+1)^n\biggl[ - \xi^{(n+1)} (\Theta^')^{(n-1)}\biggr]_{\xi=\xi_1} </math>
	<math>~=</math>	<math> - \biggl( \frac{\xi}{\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~\Theta^' \biggr]^n_{\xi=\xi_1} \, . </math>

By comparison, if we set <math>~\gamma_g = (1+1/n)</math> in the expression for the equilibrium radius that has been derived, above, from an analysis of extrema in the free energy function, we obtain,

<math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R_\mathrm{eq}^{(3-n)}</math>

<math> ~3 \biggl( \frac{5\mathfrak{f}_A}{\mathfrak{f}_W} \biggr)^n \, . </math>

So, it appears as though, quite generally,

<math>~3 \biggl( \frac{5\mathfrak{f}_A}{\mathfrak{f}_W} \biggr)^n </math>

<math> - \biggl( \frac{\xi}{\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~\Theta^' \biggr]^n_{\xi=\xi_1} \, . </math>

This is an interesting and rather unexpected result because the right-hand-side of the expression is obtained from knowledge of the dimensionless radial coordinate <math>~(\xi)</math> and the first derivative of the enthalpy structural function, <math>~\Theta_H^'</math>, whereas the left-hand-side of the expression contains a ratio of form factors that each involve definite integrals over key structural functions.

Nonrotating Configuration Embedded in an External Medium

For a nonrotating configuration <math>(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>P_e</math> of, an external medium, the statement of virial equilibrium is,

<math> (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>

Bounded Adiabatic

For adiabatic configurations <math>(\delta_{1\gamma_g} = 0)</math>, equilibrium states exist at radii given by the roots of the following expression:

<math> 3(\gamma_g-1) B\chi^{3 -3\gamma_g} ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>

Whitworth's (1981) Equivalent Relation

This is precisely the same condition that derives from setting equation (3) to zero in Whitworth's (1981, MNRAS, 195, 967) discussion of the "global gravitational stability for one-dimensional polytropes." The overlap with Whitworth's narative is perhaps clearer after introducing the algebraic expressions for the coefficients <math>A</math>, <math>B</math>, and <math>D</math>, dividing the equation through by <math>(3\chi^3 V_0) = (4\pi R^3)</math>, and rewriting <math>R</math> as <math>R_\mathrm{eq}</math> to obtain,

<math> P_e = K \biggl( \frac{3M}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} - \biggl( \frac{3GM^2}{20\pi R_\mathrm{eq}^4} \biggr) \, . </math>

This exactly matches equation (5) of Whitworth, which reads:

P-V Diagram

Returning to the dimensionless form of this expression and multiplying through by <math>[-\chi/(3D)]</math>, we obtain,

<math> \chi^4 - (\gamma_g - 1)\frac{B}{D} \chi^{4-3\gamma_g} + \frac{A}{3D} = 0 \, . </math>

Writing the coefficient, <math>B</math>, in terms of the average sound speed and setting the radial scale factor equal to the equilibrium radius of an isolated adiabatic sphere, that is, setting,

the equation governing the radii of adiabatic equilibrium states becomes,

<math> \chi^4 - \frac{1}{\Pi_a} \chi^{(4-3\gamma_g)} + \frac{1}{\Pi_a} = 0 \, , </math>

where,

<math> \Pi_a \equiv \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 \bar{c_s}^8} \, . </math>

As in the isothermal case, for a given choice of configuration mass and sound speed, this parameter, <math>\Pi_a</math>, can be viewed as a dimensionless external pressure. Alternatively, for a given choice of <math>P_e</math> and <math>\bar{c_s}</math>, <math>\Pi_a^{1/2}</math> can represent a dimensionless mass; or, for a given choice of <math>M</math> and <math>P_e</math>, <math>\Pi_a^{-1/8}</math> can represent a dimensionless sound speed. Here we will view it as a dimensionless external pressure.

Unlike the isothermal case, for an arbitrary value of the adiabatic exponent, <math>\gamma_g</math>, it isn't possible to invert this equation to obtain an analytic expression for <math>\chi</math> as a function of <math>\Pi_a</math>. But we can straightforwardly solve for <math>\Pi_a</math> as a function of <math>\chi</math>. The solution is,

<math> \Pi_a = \frac{\chi^{(4- 3\gamma_g)} - 1}{\chi^4} \, . </math>

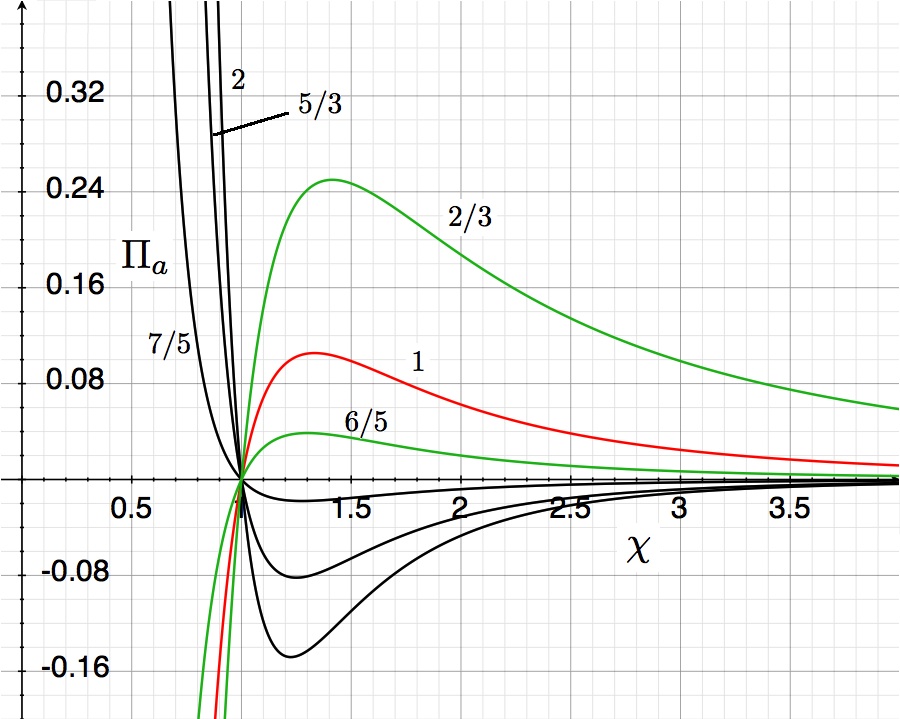
For physically relevant solutions, both <math>\chi</math> and <math>\Pi_a</math> must be nonnegative. Hence, as is illustrated by the curves in Figure 4, the physically allowable range of equilibrium radii is,

<math> 1 \le \chi \le \infty \, ~~~~~\mathrm{for}~ \gamma_g < 4/3 \, ; </math>

Figure 4: Equilibrium Adiabatic P-V Diagram

The curves trace out the function,

<math> \Pi_a = (\chi^{4-3\gamma_g} - 1)/\chi^4 \, , </math>

for six different values of <math>\gamma_g</math> (<math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled) and show the dimensionless external pressure, <math>\Pi_a</math>, that is required to construct a nonrotating, self-gravitating, uniform density, adiabatic sphere with an equilibrium radius <math>\chi</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative.

The solid red curve, drawn for the case <math>\gamma_g = 1</math>, is identical to the solid black (isothermal) curve displayed above in Figure 1.

Each of the <math>\Pi_a(\chi)</math> curves drawn in Figure 4 exhibits an extremum. In each case this extremum occurs at a configuration radius, <math>\chi_\mathrm{extreme}</math>, given by,

<math> \frac{\partial\Pi_a}{\partial\chi} = 0 \, , </math>

that is, where,

<math> 4 - 3\gamma_g \chi^{4-3\gamma_g} = 0 ~~~~\Rightarrow ~~~~~ \chi_\mathrm{extreme} = \biggl[ \frac{4}{3\gamma_g} \biggr]^{1/(4-3\gamma_g)} \, . </math>

For each value of <math>\gamma_g</math>, the corresponding dimensionless pressure is,

<math> \Pi_a \biggr|_\mathrm{extreme} = \biggl(\frac{4}{3\gamma} - 1 \biggr) \biggl[ \frac{3\gamma_g}{4} \biggr]^{4/(4-3\gamma_g)} \, . </math>

Note, first, that for <math>\gamma_g > 4/3</math>, an equilibrium configuration with a positive radius can be constructed for all physically realistic — that is, for all positive — values of <math>\Pi_a</math>. Also, consistent with the behavior of the curves shown in Figure 4, the extremum arises in the regime of physically relevant — i.e., positive — pressures only for values of <math>\gamma_g < 4/3</math>; and in each case it represents a maximum limiting pressure.

Maximum Mass

<math>n=5</math> Polytropic

When <math>\gamma_a = 6/5</math> — which corresponds to an <math>n=5</math> polytropic configuration — we obtain,

<math> \Pi_\mathrm{max} = \Pi_a\biggr|_\mathrm{extreme}^{(\gamma_g = 6/5)} = \biggl( \frac{3^{18}}{2^{10}\cdot 5^{10}} \biggr) \, , </math>

which corresponds to a maximum mass for pressure-bounded <math>n=5</math> polytropic configurations of,

<math>M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} = \biggl(\frac{3^{19}}{2^{12}\cdot 5^{7}\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} \, .</math>

This result can be compared to other determinations of the Bonnor-Ebert mass limit.

User:Tohline/SSC/Virial/Polytropes

Contents