Massless Polytropic Tori

(aka Palapoizou-Pringle Tori)

In a seminal paper that focused on an analysis of nonaxisymmetric instabilities in accretion disks, Papaloizou & Pringle (1984, MNRAS, 208, 721-750; hereafter, PP84) began by constructing equilibrium structures of axisymmetric, polytropic tori that reside in (orbit about) a point-mass potential. The derived structures have analytic prescriptions. Although the tori constructed by PP84 were not self-gravitating — i.e., the tori were massless — it is nevertheless instructive for us to examine how these equilibrium structures were derived.

Governing Relations

As has been derived elsewhere, for axisymmetric configurations that obey a barotropic equation of state, hydrostatic balance is governed by the following algebraic expression:

<math>H + \Phi_\mathrm{eff} = C_\mathrm{B} ,</math>

where <math>C_\mathrm{B}</math> is the Bernoulli constant,

<math>\Phi_\mathrm{eff} \equiv \Phi + \Psi ,</math>

and <math>\Psi</math> is the relevant centrifugal potential. For self-gravitating configurations, this algebraic expression must be satisfied in concert with a self-consistent solution of the Poisson equation, but for the massless PP84 toroidal structures, <math>~\Phi</math> is just the Newtonian potential presented by a point-like object of mass <math>M_\mathrm{pt}</math>, namely,

<math>\Phi = - \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} .</math>

Supplemental Relations

Following PP84, we supplement the above-specified set of governing equations with a polytropic equation of state, as defined in our overview of supplemental relations for time-independent problems. Specifically, we will assume that <math>~\rho</math> is related to <math>~H</math> through the relation,

<math>~H = (n+1)K_\mathrm{n} \rho^{1/n}</math> ,

or we can set,

Also following PP84, we impose a steady-state velocity flow-field that is described by a fluid with uniform specific angular momentum, <math>j_0</math>. Drawing from our table of example Simple rotation profiles, the centrifugal potential that describes this chosen flow-field is given by the expression,

<math> \Psi(\varpi) = \frac{j_0^2}{2\varpi^2} . </math>

Summary

In summary, for this problem the relevant simplified governing relation is,

<math> H = -\Phi_\mathrm{eff} + C_\mathrm{B} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \Psi + C_\mathrm{B} . </math>

Inserting the two supplemental relations into this governing algebraic expression, we conclude that the polytropic tori studied by PP84 must have structures that satisfy the equation,

<math> (n+1)\frac{P}{\rho} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \frac{j_0^2}{2\varpi^2} + C_\mathrm{B} . </math>

This is identical to Eq. (2.8) of PP84.

Solution

As PP84 point out, for these toroidal structures, it is convenient to normalize all lengths to the position in the equatorial plane, <math>\varpi_0</math>, at which a fluid particle with specific angular momentum <math>j_0</math> has an angular orbital frequency, <math>\dot\varphi = j_0/\varpi^2</math>, that matches the Keplerian orbital frequency,

<math> \omega_K \equiv \biggl[ \frac{GM_\mathrm{pt}}{\varpi^3} \biggr]^{1/2} , </math>

that is associated with the point-mass, <math>M_\mathrm{pt}</math>. That is, it is convenient to define the dimensionless coordinates,

<math> \chi \equiv \frac{\varpi}{\varpi_0} ~~~~~\mathrm{and}~~~~~ \zeta \equiv \frac{z}{\varpi_0} , </math>

where,

<math> \varpi_0 \equiv \frac{j_0^2}{GM_\mathrm{pt}} . </math>

The algebraic relation defining the equilibrium structure then becomes,

<math> H = (n+1)\frac{P}{\rho} = \frac{GM_\mathrm{pt}}{\varpi_0} \biggl[ (\chi^2 + \zeta^2)^{-1/2} - \frac{1}{2}\chi^{-2} - C_\mathrm{B}^' \biggr] , </math>

where the normalized Bernoulli constant,

<math> C_\mathrm{B}^' \equiv - \frac{C_\mathrm{B} \varpi_0}{GM_\mathrm{pt}} . </math>

Boundary Conditions

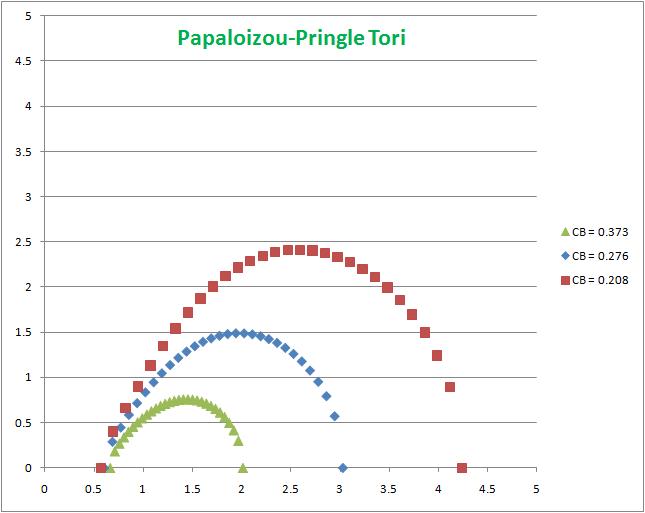
$Meridional contours of constant <math>C_\mathrm{B}^'</math>.$

The surface of the torus occurs where the enthalpy goes to zero. The meridional <math>(\chi,\zeta)</math> cross-section through three such surfaces are displayed in the accompanying figure. The displayed surfaces correspond to <math>C_\mathrm{B}^' =</math> 0.208 (red curve), 0.276 (blue curve), and 0.373 (gold curve). Properties of these tori are described in more detail in an accompanying discussion entitled, Toroidal Configurations and Related Coordinate Systems.

In the equatorial plane <math>(\zeta=0)</math>, the locations of the inner and outer edges of the torus are obtained from the roots of the equation,

<math> \chi^{-2} - 2\chi^{-1} + 2C_\mathrm{B}^' = 0 , </math>

that is, the inner <math>(\chi_-)</math> and outer <math>(\chi_+)</math> edges are located at,

<math> \chi_\pm = \frac{1}{1 \mp \sqrt{1-2C_\mathrm{B}^'}} . </math>

Clearly, the relative cross-sectional size — or, as defined in PP84, the dimensionless distortion parameter <math>\delta \equiv (\chi_+ + \chi_-)/2 = (2C_\mathrm{B}^')^{-1}</math> — is determined by the choice of the dimensionless Bernoulli constant, which must lie in the range, <math> 1 \geq 2C_\mathrm{B}^' \geq 0</math>.

Related Wikipedia Discussions

Polytrope

User:Tohline/Apps/PapaloizouPringleTori

Contents