User:Tohline/Apps/MaclaurinSpheroidSequence
Maclaurin Spheroid Sequence

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Detailed Force Balance Conditions
The essential structural elements of each Maclaurin spheroid model are uniquely determined once we specify the system's axis ratio, <math>~c/a</math>, or by the system's meridional-plane eccentricity, <math>~e</math>, where
|
<math>~e</math> |
<math>~\equiv</math> |
<math>~\biggl[1 - \biggl(\frac{c}{a}\biggr)^2\biggr]^{1 / 2} \, ,</math> |
which varies from e = 0 (spherical structure) to e = 1 (infinitesimally thin disk). According to our accompanying derivation, for a given choice of <math>~e</math>, the square of the system's equilibrium angular velocity is,
|
<math> ~ \omega_0^2 </math> |
<math> ~= </math> |
<math> 2\pi G \rho \biggl[ A_1 - A_3 (1-e^2) \biggr] \, , </math> |
where,
|
<math> ~A_1 </math> |
<math> ~= </math> |
<math> \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} - (1-e^2)^{1/2} \biggr](1-e^2)^{1/2} \, , </math> |
|
<math> ~A_3 </math> |
<math> ~= </math> |
<math> \frac{2}{e^2} \biggl[(1-e^2)^{-1/2} -\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{1/2} \, . </math> |
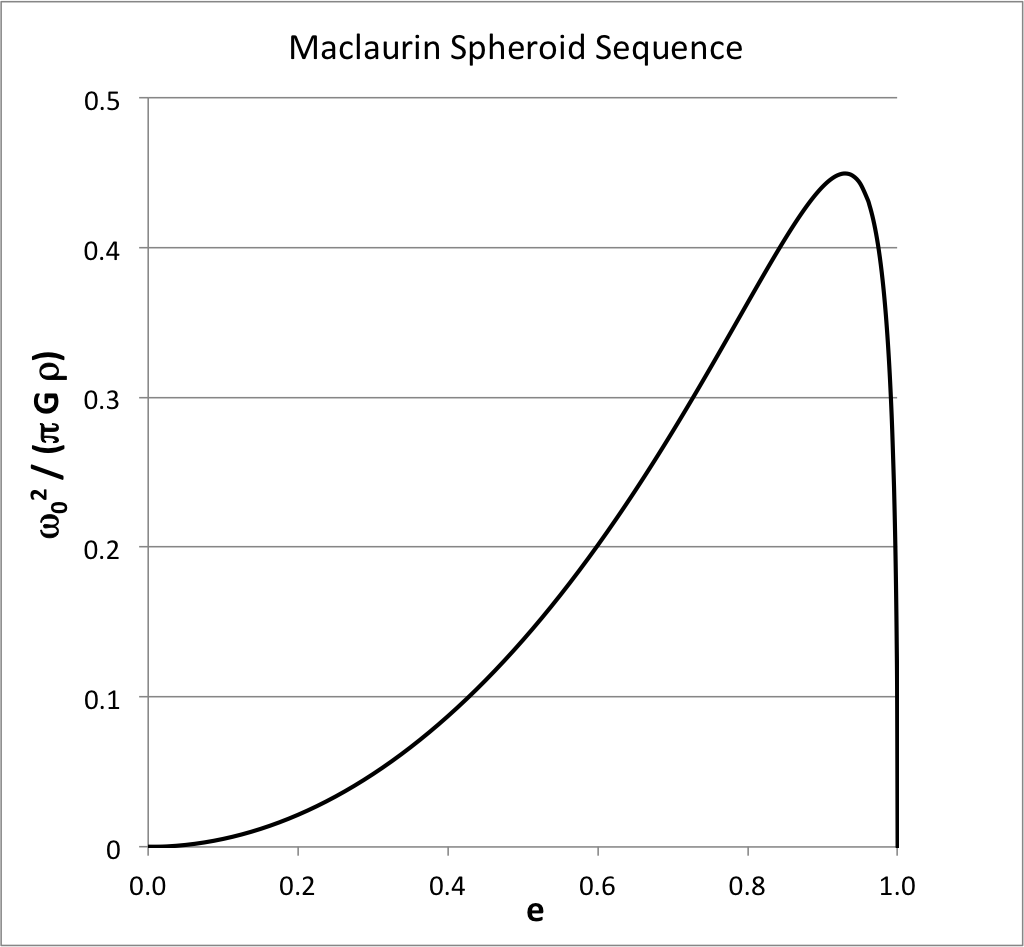
The figure shown here, on the right, essentially replicates Fig. 5 (p. 79) of EFE. It shows how the square of the angular velocity — in the unit <math>~\pi G\rho</math> — varies along the Maclaurin sequence.
See Also
- Properties of Maclaurin Spheroids
- Excerpts from Maclaurin's (1742) A Treatise of Fluxions
- Properties of Homogeneous Ellipsoids

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |