The Stability of Self-Gravitating Polytropic Tori
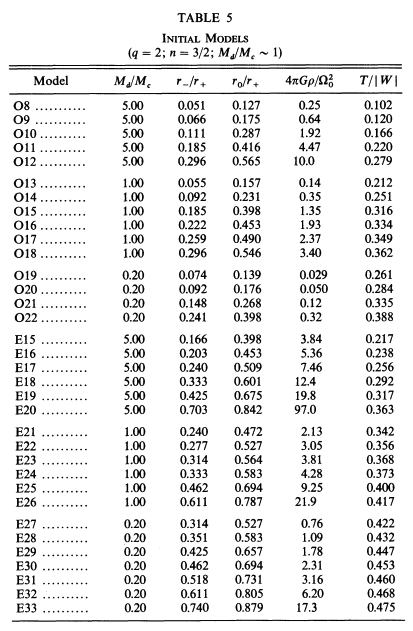
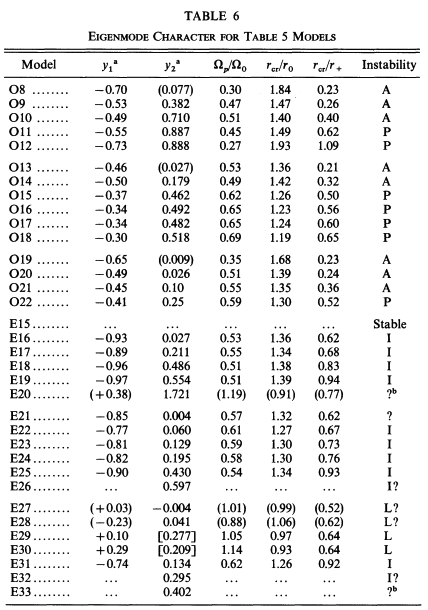
J. W. Woodward, J. E. Tohline, & I. Hachisu (1994; hereafter WTH94) used nonlinear numerical hydrodynamic techniques to examine the relative stability of self-gravitating, polytropic tori toward the development of nonaxisymmetric structure. The following pair of tables list key properties of the set of model tori that were examined: Table 5 gives characteristics of the initial models and Table 6 presents results ascertained from the numerical stability analyses.
Online Movies
| Figure 1:
Animation Sequences to Supplement Figure 10 of WTH94
(click on security-lock icon or caption model name to go to YouTube) |
|
|
|
|
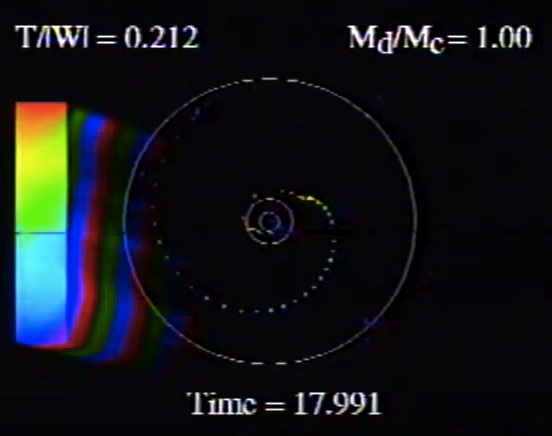
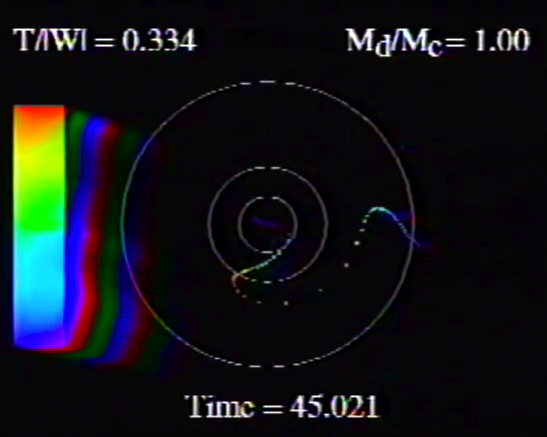
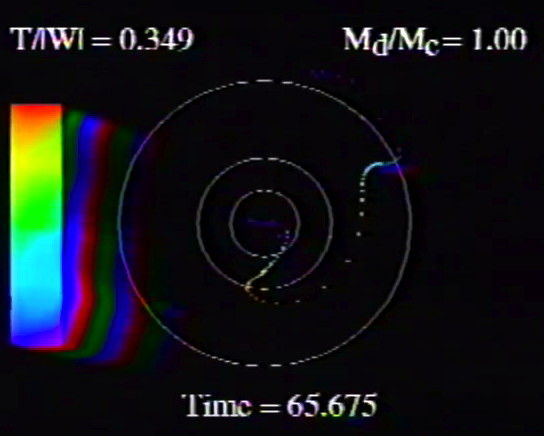
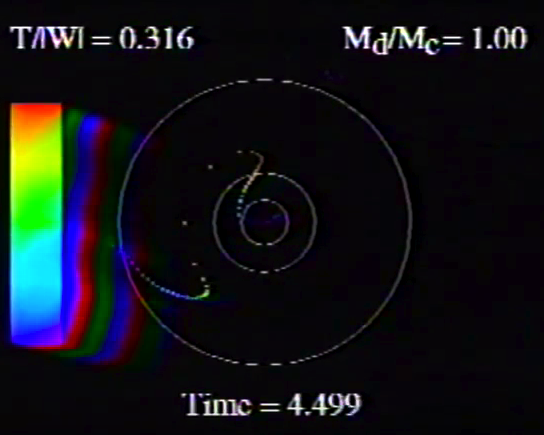
| Table 5, Model O15 |
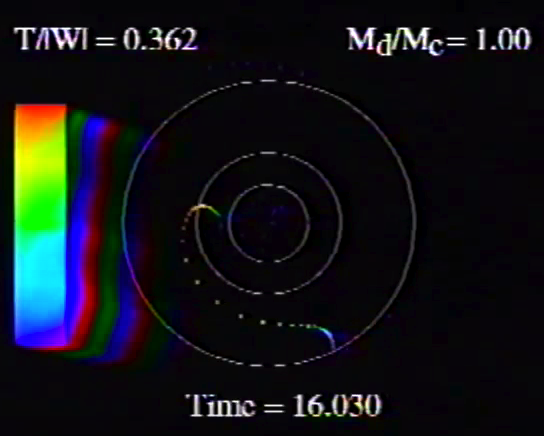
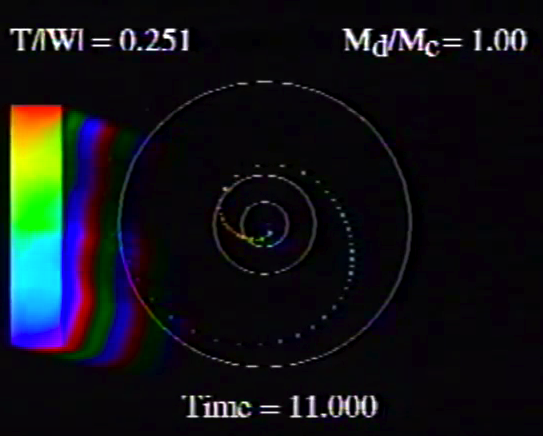
Table 5, Model O14 |
|
|
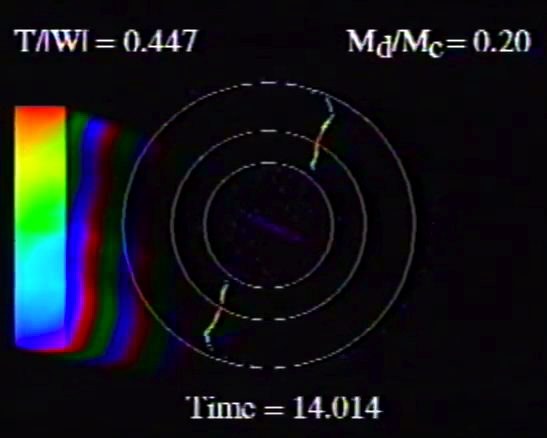
|
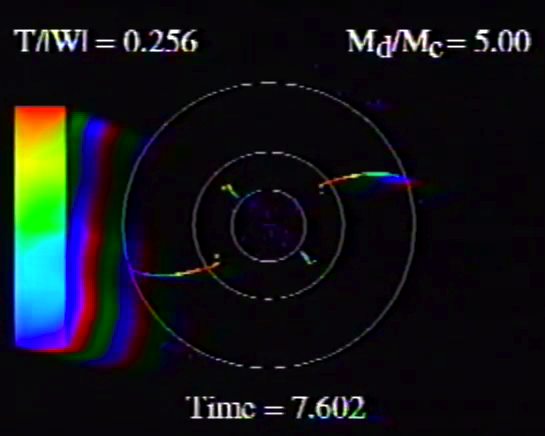
| Table 5, Model E17 |
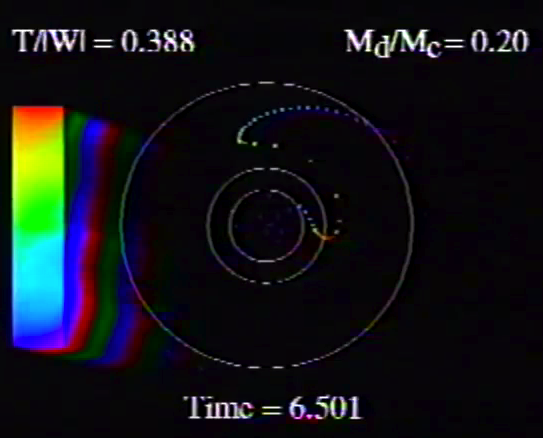
Table 5, Model E29 |
|
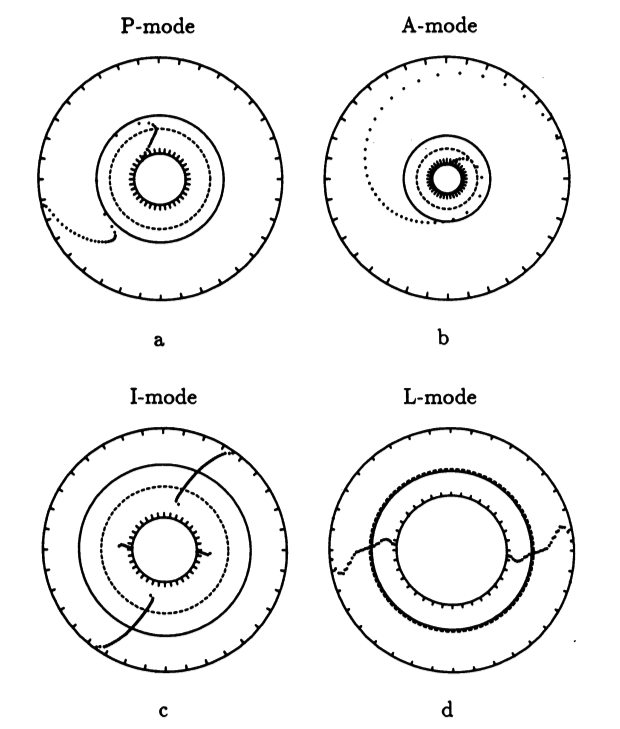
Caption to Fig. 10 from WTH94: "<math>~\phi_m - r</math>" diagrams illustrating the azimuthal structure of the four specific eigenmodes that were found to be dynamically unstable in our modeled disks. (a) The m = 1 P-mode, shown here as it developed in model O15 <math>~[M_d/M_c = 1; ~T/|W| = 0.316];</math> (b) The m = 1 A-mode, shown here as it developed in model O14 <math>~[M_d/M_c = 1; ~T/|W| = 0.251];</math> (c) The m = 2 I-mode, shown here as it developed in model E17 <math>~[M_d/M_c = 5; ~T/|W| = 0.256];</math> (d) The m = 2 L-mode, shown here as it developed in model E29 <math>~[M_d/M_c = 0.2; ~T/|W| = 0.447]\, .</math>
|