Marginally Unstable Bipolytropes

Our aim is to determine whether or not there is a relationship between equilibrium models at turning points along bipolytrope sequences and bipolytropic models that are marginally (dynamically) unstable toward collapse (or dynamical expansion).

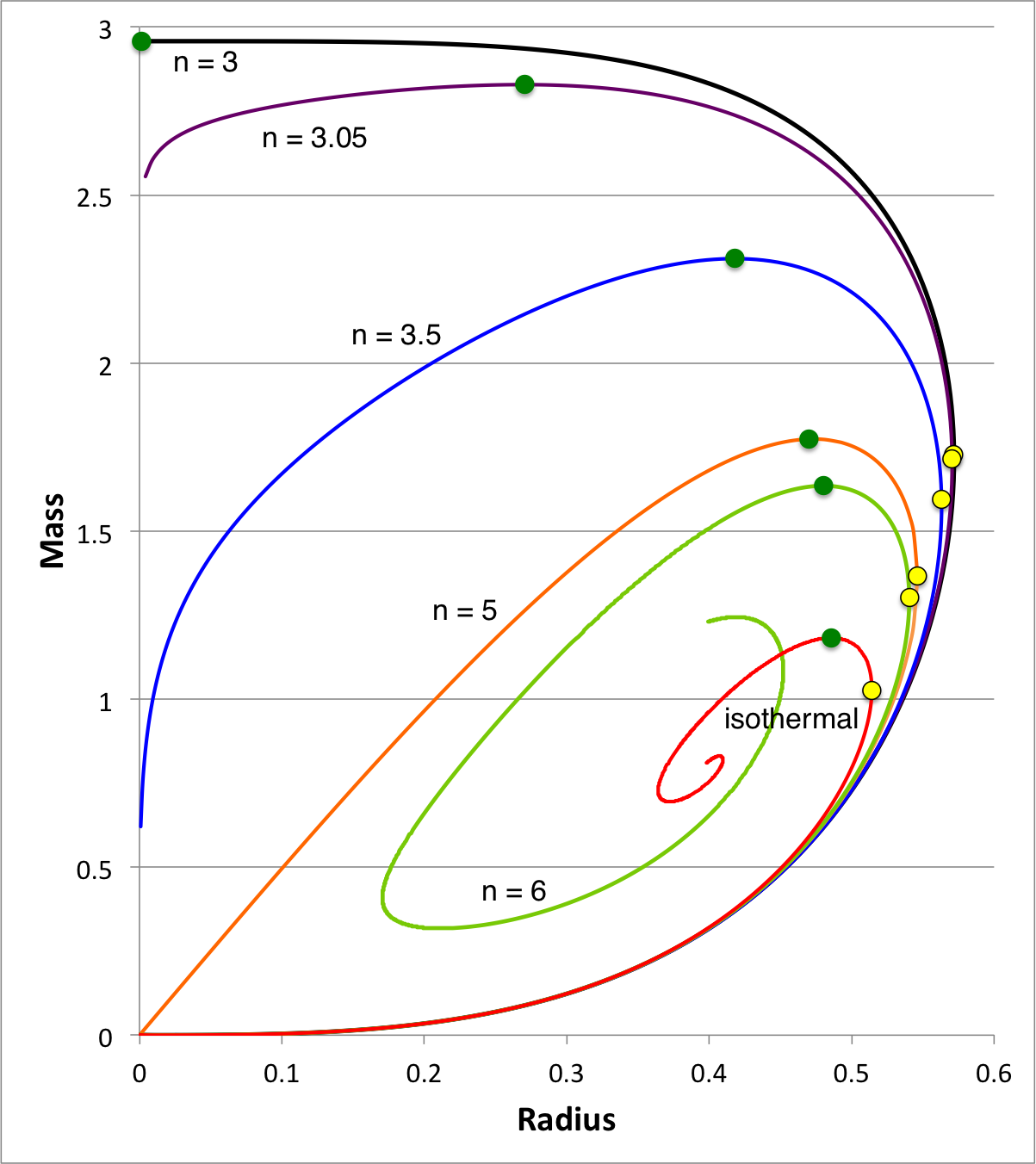
Figure 1: Equilibrium Sequences of Pressure-Truncated Polytropes

We expect the content of this chapter — which examines the relative stability of bipolytropes — to parallel in many ways the content of an accompanying chapter in which we have successfully analyzed the relative stability of pressure-truncated polytopes. Figure 1, shown here on the right, has been copied from that separate discussion. The curves show the mass-radius relationship for pressure-truncated model sequences having a variety of polytropic indexes, as labeled, over the range <math>3 \le n \le \infty</math>. On each sequence, the green filled circle identifies the model with the largest mass. We have shown that the oscillation frequency of the fundamental-mode of radial oscillation is precisely zero for each one of these maximum-mass models. As a consequence, we know that each green circular marker identifies the point along its associated sequence that separates dynamically stable from dynamically unstable models.

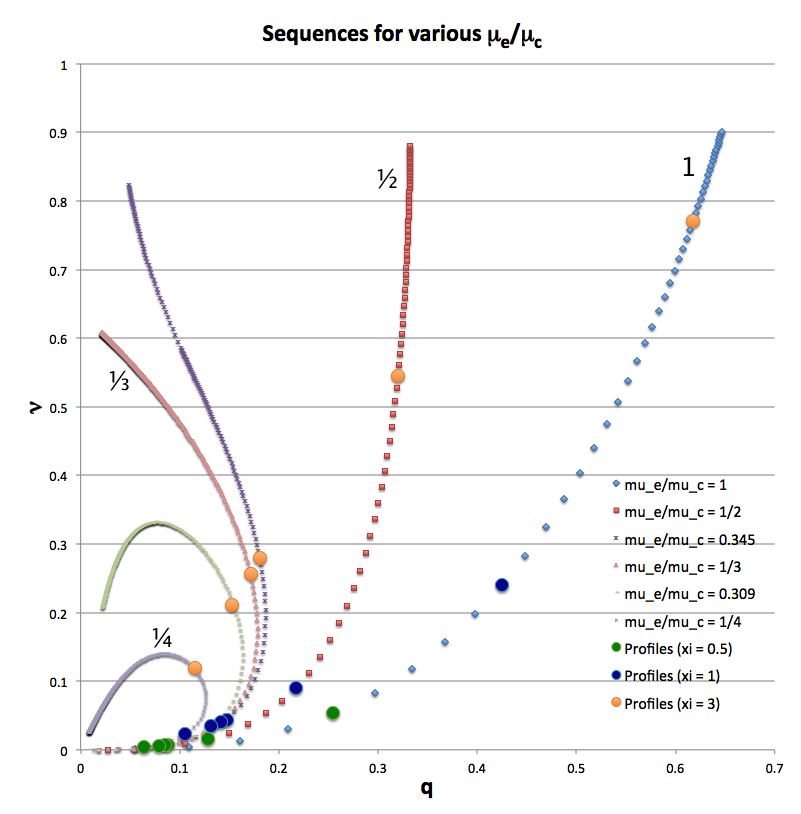
For a given choice of <math>~\mu_e/\mu_c</math> a physically relevant sequence of models can be constructed by steadily increasing the value of <math>\xi_i</math> from zero to infinity — or at least to some value, <math>\xi_i \gg 1</math>. Figure 2 shows how the fractional core mass, <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>, varies with the fractional core radius, <math>q \equiv r_\mathrm{core}/R</math>, along sequences having six different values of <math>~\mu_e/\mu_c</math>, as detailed in the figure caption. The natural expectation is that an increase in <math>\xi_i</math> along a given sequence will correspond to an increase in the relative size — both the radius and the mass — of the core. This expectation is realized along the sequences marked by blue diamonds (<math>~\mu_e/\mu_c = 1</math>) and by red squares (<math>~\mu_e/\mu_c = </math>½). But the behavior is different along the other four illustrated sequences. For sufficiently large <math>~\xi_i</math>, the relative radius of the core begins to decrease; then, as <math>~\xi_i</math> is pushed to even larger values, eventually the relative core mass begins to decrease. Additional properties of these equilibrium sequences are discussed in an accompanying chapter.

Figure 2:

Figure 2: Analytically determined plot of fractional core mass (<math>~\nu</math>) versus fractional core radius (<math>~q</math>) for <math>~(n_c, n_e) = (5, 1)</math> bipolytrope model sequences having six different values of <math>~\mu_e/\mu_c</math>: 1 (blue diamonds), ½ (red squares), 0.345 (dark purple crosses), ⅓ (pink triangles), 0.309 (light green dashes), and ¼ (purple asterisks). Along each of the model sequences, points marked by solid-colored circles correspond to models whose interface parameter, <math>~\xi_i</math>, has one of three values: 0.5 (green circles), 1 (dark blue circles), or 3 (orange circles); the images linked to Table 2 provide plots of the density, pressure and mass profiles for nine of these identified models.

User:Tohline/SSC/Stability/BiPolytropes

Contents

Marginally Unstable Bipolytropes

See Also

Navigation menu

Search