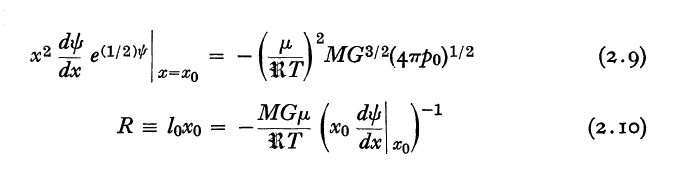Radial Oscillations of Pressure-Truncated Isothermal Spheres

Here we draw primarily from the following three sources:

§5.3.8 (p. 372) of Horedt's (2004) treatise on Polytropes: Applications in Astrophysics and Related Fields
S. Yabushita (1968, MNRAS, 140, 109) — Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres
L. G. Taff & H. M. Horn (1974, MNRAS, 168, 427-432) — Radial Pulsations of Finite Isothermal Gas Spheres

Groundwork

Equilibrium Model

In an accompanying discussion, while reviewing the original derivations of Ebert (1955) and Bonnor (1956), we have detailed the equilibrium properties of pressure-truncated isothermal spheres. A parallel presentation of these details can be found in §2 — specifically, equations (2.4) through (2.10) — of Yabushita (1968). Each of Yabushita's key mathematical expressions can be mapped to ours via the variable substitutions presented here in Table 1.

Table 1: Mapping from Yabushita's (1968) Notation to Ours
Yabushita's (1968) Notation:	<math>~x</math>	<math>~\psi</math>	<math>~\mu</math>	<math>~M</math>	<math>~x_0</math>	<math>~p_0</math>
Our Notation:	<math>~\xi</math>	<math>~-\psi</math>	<math>~\bar\mu</math>	<math>~M_{\xi_e}</math>	<math>~\xi_e</math>	<math>~P_e</math>

For example, given the system's sound speed, <math>~c_s</math>, and total mass, <math>~M_{\xi_e}</math>, the expression from our presentation that shows how the bounding external pressure, <math>~P_e</math>, depends on the dimensionless Lane-Emden function, <math>~\psi</math>, is,

<math>~P_e</math>	<math>~=</math>	<math>~\biggl( \frac{c_s^8}{4\pi G^3 M_{\xi_e}^2} \biggr) ~\xi_e^4 \biggl(\frac{d\psi}{d\xi}\biggr)^2_e e^{-\psi_e}</math>
<math>~\Rightarrow ~~~ \xi_e^2 \biggl(-\frac{d\psi}{d\xi}\biggr)_e e^{-(1/2)\psi_e}</math>	<math>~=</math>	<math>~\frac{1}{c_s^4}\biggl[ G^3 M_{\xi_e}^2 ~(4\pi P_e)\biggr]^{1 / 2} \, ,</math>

which — see the boxed-in excerpt that follows — exactly matches Yabushita's (1968) equation (2.9), after recalling that the system's sound speed is related to its temperature via the relation,

And, our expression for the truncated configuration's equilibrium radius is,

<math>~\frac{GM_{\xi_e}}{c_s^2} \biggl[ - \xi \biggl(\frac{d\psi}{d\xi}\biggr) \biggr]_e^{-1}</math>

which — see the boxed-in excerpt that follows — matches Yabushita's (1968) equation (2.10).

Equations extracted^† from S. Yabushita (1968, MNRAS, 140, 109)

"Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres"

MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society

^†Mathematical expressions displayed here with layout modified from the original publication.

Linearized Wave Equation

In an accompanying discussion, we derived the so-called,

Wave Equation for Self-Gravitating Fluids
<math>~\frac{\partial^2 s }{\partial t^2} + \frac{\nabla\rho_0}{\rho_0} \cdot \frac{\partial \vec{v}}{\partial t} </math>	<math>~=</math>	<math>4\pi G \rho_0 s + \nabla^2\biggl[s \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] </math>

that describes the time-variation at any point in space of the fractional density fluctuation,

<math>s \equiv \frac{\rho_1}{\rho_0} \, .</math>

Multiplying this differential equation through by <math>~\rho_0</math>, and making two substitutions from our accompanying summary of the separately linearized principal governing equations — namely,

<math> ~\frac{\partial \vec{v}}{\partial t} = - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 \, , </math>

and,

<math> P_1 = \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1 ~~~ \Rightarrow ~~~ s \biggl( \frac{dP}{d\rho} \biggr)_0 = \frac{P_1}{\rho_0} \, , </math>

— gives,

<math>~\frac{\partial^2 \rho_1 }{\partial t^2} + \nabla\rho_0 \cdot \biggl[ - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0\biggr] </math>	<math>~=</math>	<math>4\pi G \rho_0 \rho_1 + \rho_0\nabla^2\biggl[\frac{P_1}{\rho_0} \biggr] </math>
<math>~\Rightarrow ~~~ \frac{\partial^2 \rho_1 }{\partial t^2} + \nabla\rho_0 \cdot \biggl[ - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 - \frac{\rho_1}{\rho_0} \nabla \Phi_0\biggr] </math>	<math>~=</math>	<math>4\pi G \rho_0 \rho_1 + \nabla^2 P_1 + P_1 \rho_0\nabla^2\biggl[\frac{1}{\rho_0} \biggr] </math>
<math>~\Rightarrow ~~~ \frac{\partial^2 \rho_1 }{\partial t^2} - \nabla^2 P_1 - 4\pi G \rho_0 \rho_1 - \nabla\rho_0 \cdot \nabla\Phi_1 - \nabla \Phi_0 \cdot \nabla\rho_1 </math>	<math>~=</math>	<math> \nabla\rho_0 \cdot \biggl[ \frac{1}{\rho_0} \nabla P_1\biggr] + P_1 \rho_0\nabla^2\biggl[\frac{1}{\rho_0} \biggr] + \nabla \Phi_0 \cdot \biggl[ \frac{\rho_1}{\rho_0} \nabla\rho_0 -\nabla\rho_1 \biggr] </math>
	<math>~=</math>	<math> -\rho_0 \nabla\biggl(\frac{1}{\rho_0}\biggr) \cdot \nabla P_1 + P_1 \rho_0\nabla^2\biggl[\frac{1}{\rho_0} \biggr] - \rho_0\nabla \Phi_0 \cdot \biggl[ \rho_1 \nabla\biggl(\frac{1}{\rho_0}\biggr) + \biggl(\frac{1}{\rho_0}\biggr)\nabla\rho_1 \biggr] </math>
	<math>~=</math>	<math> \rho_0 \biggl[ P_1 \nabla^2\biggl(\frac{1}{\rho_0} \biggr) - \nabla\biggl(\frac{1}{\rho_0}\biggr) \cdot \nabla P_1 \biggr] + \nabla P_0 \cdot \nabla\biggl(\frac{\rho_1}{\rho_0}\biggr) </math>

Alternative Expression

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations.

User:Tohline/SSC/Stability/Isothermal

Contents

Radial Oscillations of Pressure-Truncated Isothermal Spheres

Groundwork

Equilibrium Model

Linearized Wave Equation

Alternative Expression

See Also

Navigation menu

Search