Stability Analyses of PP Tori (Part 2)

This is a direct extension of our Part 1 discussion. Here we continue our effort to check the validity of the Blaes85 eigenvector. The relevant reference is:

Blaes (1985), MNRAS, 216, 553 (aka Blaes85) — Oscillations of slender tori.

Start From Scratch

Basic Equations from Blaes85

			Blaes85 Eq. No.
<math>~(\beta\eta)^2</math>	<math>~=</math>	<math>~x^2(1+xb) \, ;</math>	(2.6)
<math>~b</math>	<math>~\equiv</math>	<math>~3\cos\theta - \cos^3\theta \, ;</math>	(2.6)
<math>~f</math>	<math>~=</math>	<math>~1-\eta^2 \, .</math>	(2.5)

			Blaes85 Eq. No.
<math>~LHS \equiv \hat{L}W</math>	<math>~=</math>	<math> ~fx^2 \cdot \frac{\partial^2 W}{\partial x^2} + f \cdot \frac{\partial^2 W}{\partial \theta^2} + \biggl[ \frac{fx(1-2x\cos\theta)}{(1-x\cos\theta)} + nx^2\cdot \frac{\partial f}{\partial x}\biggr]\frac{\partial W}{\partial x} </math>
		<math> + \biggl[ \frac{fx\sin\theta}{(1-x\cos\theta)} + n\cdot \frac{\partial f}{\partial \theta}\biggr]\frac{\partial W}{\partial \theta} + \biggl[ \frac{2nx^2m^2}{\beta^2(1-x\cos\theta)^4} - \frac{m^2 x^2 f}{(1-x\cos\theta)^2} \biggr]W </math>	(4.2)
<math>~RHS</math>	<math>~=</math>	<math> ~-\frac{2nm^2}{\beta^2} \cdot (\beta\eta)^2 \biggl[ M \biggl(\frac{\nu}{m}\biggr)^2 + \frac{N}{m} \biggl(\frac{\nu}{m}\biggr)\biggr] W </math>	(4.1)
	<math>~=</math>	<math> ~-\frac{2nm^2}{\beta^2} \biggl[ x^2 \biggl(\frac{\nu}{m}\biggr)^2 + \frac{2x^2}{(1-x\cos\theta)^2} \biggl(\frac{\nu}{m}\biggr)\biggr] W </math>	(4.2)
<math>~\frac{W}{A_{00}}</math>	<math>~=</math>	<math> ~1 + \beta^2 m^2 \biggl\{ 2\eta^2\cos^2\theta - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2} ~\pm~i~\biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \eta\cos\theta \biggr\} </math>	(4.13)
<math>~\frac{\nu}{m}</math>	<math>~=</math>	<math> ~-1 ~\pm ~ i~\biggl[ \frac{3}{2(n+1)} \biggr]^{1/2} \beta </math>	(4.14)

Our Manipulation of These Equations

Analytic

<math>~\Lambda \equiv \frac{2^2(n+1)^2}{m^2}\biggl[\frac{W}{A_{00}}-1\biggr]</math>	<math>~=</math>	<math>~\beta^2 \biggl\{ 2^3(n+1)^2 \eta^2\cos^2\theta - 3\eta^2(n+1)^2 - (4n+1) ~\pm~i~[ 2^7\cdot 3(n+1)^3 ]^{1/2} \eta\cos\theta \biggr\} </math>
	<math>~=</math>	<math>~- (4n+1)\beta^2 + (\beta\eta)^2 (n+1)^2[ 2^3 \cos^2\theta - 3] ~\pm~i~\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta \, ; </math>
<math>~\Rightarrow~~~~\frac{W}{A_{00}} </math>	<math>~=</math>	<math>~1+ \biggl[ \frac{m}{2(n+1)} \biggr]^2 \Lambda </math>

<math>~\frac{LHS}{A_{00}} </math>	<math>~=</math>	<math>~\biggl[ \frac{m}{2(n+1)} \biggr]^2 f ~\biggl[ x^2 \cdot \frac{\partial^2 \Lambda}{\partial x^2} + \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \biggl[ \frac{m}{2(n+1)} \biggr]^2\biggl[ \frac{fx(1-2x\cos\theta)}{(1-x\cos\theta)} + nx^2\cdot \frac{\partial f}{\partial x}\biggr]\frac{\partial \Lambda}{\partial x} </math>
		<math> + \biggl[ \frac{m}{2(n+1)} \biggr]^2\biggl[ \frac{fx\sin\theta}{(1-x\cos\theta)} + n\cdot \frac{\partial f}{\partial \theta}\biggr]\frac{\partial \Lambda}{\partial \theta} + \biggl[ \frac{2nx^2m^2}{\beta^2(1-x\cos\theta)^4} - \frac{m^2 x^2 f}{(1-x\cos\theta)^2} \biggr]\biggl\{1+ \biggl[ \frac{m}{2(n+1)} \biggr]^2 \Lambda\biggr\} </math>
	<math>~=</math>	<math>~\biggl[ \frac{m}{2(n+1)} \biggr]^2 f \biggl\{ ~\biggl[ x^2 \cdot \frac{\partial^2 \Lambda}{\partial x^2} + \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \biggl[ \frac{x(1-2x\cos\theta)}{(1-x\cos\theta)} \biggr]\frac{\partial \Lambda}{\partial x} + \biggl[ \frac{x\sin\theta}{(1-x\cos\theta)} \biggr]\frac{\partial \Lambda}{\partial \theta} - \biggl[ \frac{m^2 x^2 }{(1-x\cos\theta)^2} \biggr] \biggl[ \frac{2^2(n+1)^2}{m^2} + \Lambda\biggr]\biggr\} </math>
		<math> + n\biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl\{ x^2\cdot \frac{\partial f}{\partial x}\cdot \frac{\partial \Lambda}{\partial x} ~+~ \frac{\partial f}{\partial \theta}\cdot \frac{\partial \Lambda}{\partial \theta} ~+~ \biggl[ \frac{2x^2m^2}{\beta^2(1-x\cos\theta)^4} \biggr]\biggl[ \frac{2^2(n+1)^2}{m^2} + \Lambda\biggr]\biggr\} </math>
	<math>~=</math>	<math>~\frac{x^2 f}{(1-x\cos\theta)^2} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl\{ ~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] - [ 2^2(n+1)^2 + m^2\Lambda ]\biggr\} </math>
		<math> + ~\frac{x^2 n}{\beta^2(1-x\cos\theta)^4} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl\{\beta^2 (1-x\cos\theta)^4\biggl[ \frac{\partial f}{\partial x}\cdot \frac{\partial \Lambda}{\partial x} ~+~ \frac{1}{x^2}\cdot \frac{\partial f}{\partial \theta}\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] ~+~ [ 2^3(n+1)^2 + 2m^2\Lambda ]\biggr\} \, . </math>

Also,

<math>~\frac{RHS}{A_{00}}</math>	<math>~=</math>	<math> ~-\frac{2n x^2}{\beta^2(1-x\cos\theta)^2} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl[ (1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)^2 + 2\biggl(\frac{\nu}{m}\biggr)\biggr] [ 2^2(n+1)^2 + m^2\Lambda ] </math>
	<math>~=</math>	<math> ~-\frac{x^2n}{\beta^2(1-x\cos\theta)^4} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl[ (1-x\cos\theta)^4\biggl(\frac{\nu}{m}\biggr)^2 + 2(1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)\biggr] [ 2^3(n+1)^2 + 2m^2\Lambda ] \, . </math>

Putting the two together implies,

Definition of Eigenvalue Problem Associated with the Stability of Slim, Papaloizou-Pringle Tori

<math>~0</math>	<math>~=</math>	<math>~\frac{1}{x^2}\biggl[\frac{LHS}{A_{00}} - \frac{RHS}{A_{00}}\biggr]\biggl[ \frac{2(n+1)}{m} \biggr]^2 (1-x\cos\theta)^4</math>
	<math>~=</math>	<math>~f (1-x\cos\theta)^2 \biggl\{ ~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] - [ 2^2(n+1)^2 + m^2\Lambda ]\biggr\} </math>
		<math> + ~\frac{n}{\beta^2} \biggl\{ (1-x\cos\theta)^4\biggl[ \frac{\partial \Lambda}{\partial x} \cdot \frac{\partial (\beta^2 f)}{\partial x} ~+~ \frac{\partial \Lambda}{\partial \theta} \cdot \frac{\partial (\beta^2 f/x^2)}{\partial \theta} \biggr] ~+~ \biggl[ (1-x\cos\theta)^4\biggl(\frac{\nu}{m}\biggr)^2 + 2(1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] [ 2^3(n+1)^2 + 2m^2\Lambda ] \biggr\} \, . </math>

The first line of this governing, two-line expression contains the function, <math>~f</math>, as a leading factor, while the leading factor in the second line is the ratio, <math>~n/\beta^2</math>. Presumably the three terms (hereafter, TERM1, TERM2, & TERM3, respectively) inside the curly brackets on the first line must cancel — to a sufficiently high order in <math>~x</math> — and, independently, the two terms (hereafter, TERM4 & Term5, respectively) inside the curly brackets on the second line must cancel. Furthermore, these cancellations must occur separately for the real parts and the imaginary parts of each bracketed expression.

Example Evaluation

Evaluating various terms using the parameter set, <math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math> as begun in our "Part 1" analysis, we have:

TERM1	<math>~\equiv</math>	<math>~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] </math>
	<math>~=</math>	<math>~ \biggl(\frac{7}{2^3} \biggr)^2\biggl\{ \frac{65}{2^3} + \frac{1}{2^4}\cdot [~4.269531250~] \biggr\} ~\pm~i~\biggl(\frac{7}{2^3} \biggr)^2\biggl\{ [~30.76957507~] + \frac{1}{2^4}\cdot (-1)[~5.773638858~] \biggr\}\beta </math>
	<math>~=</math>	<math>~ \frac{7^2}{2^6} [ ~8.39184570 ~\pm~i~30.40872264~\beta] \, . </math>
TERM2	<math>~\equiv</math>	<math>~\frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] </math>
	<math>~=</math>	<math>~ \frac{7}{2^5} [ ~-0.931640625 ~\pm~i~13.86780926~\beta] \, . </math>
TERM3	<math>~\equiv</math>	<math>~- [ 2^2(n+1)^2 + m^2\Lambda ] </math>
	<math>~=</math>	<math>~ -\biggl\{~2^4 + m^2[~- 5\beta^2 + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr\}\, . </math>

The sum of these three terms gives,

TERM1 + TERM2 + TERM3	<math>~=</math>	<math>~ \frac{7^2}{2^6} [ ~8.39184570 ~\pm~i~30.40872264~\beta] +\frac{7}{2^5} [ ~-0.931640625 ~\pm~i~13.86780926~\beta] </math>
		<math>~ -\biggl\{~2^4 + m^2[~- 5\beta^2 + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr\} </math>
	<math>~=</math>	<math>~ 6.42500686 - 0.20379639 -~2^4 + 5m^2\beta^2 - m^2 0.167968750 </math>
		<math>~ \pm~i~\biggl[23.28167827 + 3.03358328 - 8.031189202 ~m^2~\biggr]\beta </math>
	<math>~=</math>	<math>~ -9.77878953+ 5m^2\beta^2 - m^2 0.167968750 ~ \pm~i~\biggl[26.31526155- 8.031189202 ~m^2\biggr]\beta </math>

We also need to know that,

<math>~f(1-x\cos\theta)^2</math>	<math>~=</math>	<math>~(1-\eta^2)(1-2x\cos\theta + x^2\cos^2\theta)</math>
	<math>~=</math>	<math>~\biggl\{ 1-\biggl(\frac{x}{\beta}\biggr)^2\biggl[1+\beta\biggl(\frac{x}{\beta}\biggr) b\biggr] \biggr\} \biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr]</math>

Moving on to the last pair of terms …

TERM4	<math>~=</math>	<math>~ -x \ell^4\biggl[ (2+3xb)\cdot \frac{\partial\Lambda}{\partial x} - 3\sin^3\theta \cdot \frac{\partial\Lambda}{\partial \theta} \biggr] </math>
	<math>~=</math>	<math>~ -x \ell^4\biggl[ (2+3xb)\cdot [~1.515625000~\pm~i~36.23373732 ~\beta] - 3\sin^3\theta \cdot [~-2.388335684~\pm~i~(-1)15.36617018 ~\beta] \biggr] </math>
	<math>~=</math>	<math>~ -x\ell^4 [~9.248046874~\pm~i~139.7753772~\beta] </math>

TERM5 (Case B)	<math>~=</math>	<math>~ \biggl[ \ell^4 [1-0.75\beta^2~\pm~i~(-1)\sqrt{3}\beta] +2\ell^2[ -1~\pm~i~\sqrt{0.75}\beta ] + 1 \biggr] \cdot \biggl[~2^5 + 2\cancelto{1}{m^2}[~- 5\beta + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] \cdot \biggl[~[2^5 - 10\beta + (2)0.167968750]~\pm~i~[(2)8.031189202 ~\beta]~\biggr] </math>
		<math>~ \pm~\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[~i~ [2^5 - 10\beta + (2)0.167968750]~-~[(2)8.031189202 ~\beta]~\biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] \cdot \biggl[~[2^5 - 10\beta + (2)0.167968750]\biggr] \pm~(-1)\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[[(2)8.031189202 ~\beta]~\biggr] </math>
		<math>~ \pm~i~\biggl\{\biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] \cdot \biggl[[(2)8.031189202 ~\beta]~\biggr] +~\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[~ [2^5 - 10\beta + (2)0.167968750]~\biggr] \biggr\} \, . </math>

Evaluating this TERM5 expression for the case of <math>~\beta = 1</math>, we have,

TERM5 (Case B)	<math>~=</math>	<math>~ \biggl[ 0.25\ell^4 - 2\ell^2 + 1 \biggr] \cdot \biggl[~[2^5 - 10 + (2)0.167968750]\biggr] \pm~(-1)\sqrt{3}\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[[(2)8.031189202 ]~\biggr] </math>
		<math>~ \pm~i~\biggl\{\biggl[ \ell^4 [1-0.75] - 2\ell^2 + 1 \biggr] \cdot \biggl[[(2)8.031189202]~\biggr] +~\sqrt{3}\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[~ [2^5 - 10 + (2)0.167968750]~\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ [ -0.38470459 ] \cdot [22.3359375] \pm~(-1)[ ~0.31080502 ] \cdot [~16.0623784 ~] </math>
		<math>~ \pm~i~\biggl\{[ -0.38470459 ] \cdot [~16.0623784 ~] +~[ ~0.31080502 ] \cdot [22.3359375]\biggr\} </math>
	<math>~=</math>	<math>~[~-13.58500545~] \pm~i~[~0.76285080~] \, . </math>

Testing for Expected Cancellations

Note first that, adopting the shorthand notation,

<math>~\ell</math>	<math>~\equiv</math>	<math>~(1-x\cos\theta)</math>
<math>~\Rightarrow ~~~~\ell^2</math>	<math>~=</math>	<math>~1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \, ;</math>
<math>~\ell^3</math>	<math>~=</math>	<math>~1-3\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 3\beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \, ;</math>
<math>~\ell^4</math>	<math>~=</math>	<math>~1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \, .</math>

Real Parts

TERM1

<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM1}}{\ell^2}\biggr]</math>	<math>~=</math>	<math>~ 2(n+1)[2^3(n+1)\cos^2\theta -3](1+3xb) +2^4(n+1)^2(\sin^2\theta - \cos^2\theta) </math>
		<math>~ + \beta\biggl(\frac{x}{\beta}\biggr) \biggl[ -2^4\cdot 3 (n+1)^2\cos^3\theta + 2^4(n+1)^2\cos^5\theta + 3^2(n+1)(16n +19)\sin^2\theta \cos\theta -2^3\cdot 23 (n+1)^2\sin^2\theta \cos^3\theta \biggr] </math>
	<math>~=</math>	<math>~ 2^4(n+1)^2\cos^2\theta -6(n+1) +2^4(n+1)^2(1 - 2\cos^2\theta) +3b\beta\biggl(\frac{x}{\beta}\biggr)\biggl[2^4(n+1)^2\cos^2\theta -6(n+1) \biggr] </math>
		<math>~ + \beta\biggl(\frac{x}{\beta}\biggr) \biggl[ -2^4\cdot 3 (n+1)^2\cos^3\theta + 2^4(n+1)^2\cos^5\theta + 3^2(n+1)(16n +19)\sin^2\theta \cos\theta -2^3\cdot 23 (n+1)^2\sin^2\theta \cos^3\theta \biggr] </math>
	<math>~=</math>	<math>~ -6(n+1) +2^4(n+1)^2(1 - \cos^2\theta) +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{2^4\cdot 3 (n+1)^2 [3\cos^2\theta -\cos^4\theta] -18(n+1)[3-\cos^2\theta] </math>
		<math>~ -2^4\cdot 3 (n+1)^2\cos^2\theta + 2^4(n+1)^2\cos^4\theta + 3^2(n+1)(16n +19)(1-\cos^2\theta) -2^3\cdot 23 (n+1)^2 (\cos^2\theta - \cos^4\theta) \biggr\} </math>

TERM2

<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM2}}{\ell}\biggr]</math>	<math>~=</math>	<math>~ (n+1)[-6 + 2^4(n+1)\cos^2\theta] </math>
		<math>~ - x (n+1)\cos\theta \{ [ 15 + 2^4(n+1) ] -\cos^2\theta[9 + 2^3\cdot 7 (n+1)] +2^3\cdot 3(n+1)\cos^4\theta \} </math>
		<math>~ +x^2(n+1) \{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \} </math>

TERM4

<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math>	<math>~=</math>	<math>~ \biggl\{ (n+1)[2^3(n+1)\cos^2\theta -3]x(2+3xb)\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] </math>
		<math>~ +~ (n+1)\sin\theta \biggl\{ -2^4 (n+1) (\beta\eta)^2 \cos\theta + 3x^3 \sin^2\theta \biggl[3 - 2^3(n+1)\cos^2\theta \biggr] \biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] </math>
	<math>~=</math>	<math>~ -~(n+1)[2^3(n+1)\cos^2\theta -3]x^2(2+3xb)^2 </math>
		<math>~ -~ 3x^3(n+1)\sin^4\theta \biggl\{ 2^4 (n+1) (1+xb) \cos\theta + 3x \sin^2\theta [2^3(n+1)\cos^2\theta -3] \biggr\} </math>
	<math>~=</math>	<math>~ -~x^2 \cdot 2^2 (n+1)[2^3(n+1)\cos^2\theta -3]\biggl(1+\frac{3xb}{2}\biggr)^2 </math>
		<math>~ -~ x^3 \cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) ~-~x^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta -3] \, .</math>
	<math>~=</math>	<math>~ -x\biggl\{~x[~18.37695315~] + x^2[~72.5625~] + x^3[~7.59375~]~~\biggr\} = -x[~9.24804688~]\, . </math>

Or, continuing to develop the analytic power-law expression,

<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math>	<math>~=</math>	<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 (n+1)[2^3(n+1)\cos^2\theta -3] \biggl[4 + 12\beta \biggl( \frac{x}{\beta}\biggr)b + 9 \beta^2\biggl( \frac{x}{\beta}\biggr)^2 b^2 \biggr] </math>
		<math>~ -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta \biggl[ 1+\beta \biggl( \frac{x}{\beta}\biggr)b \biggr] ~-~\beta^4 \biggl( \frac{x}{\beta}\biggr)^4 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta -3] </math>
	<math>~\approx</math>	<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] -~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta </math>
<math>~\Rightarrow ~~~ \mathrm{Re}\biggl[\mathrm{TERM4}\biggr]</math>	<math>~\approx</math>	<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] -~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b </math>
		<math>~ -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta +~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^4 (n+1)[2^3(n+1)\cos^2\theta -3] \cos\theta </math> \, .

TERM5

Now, let's examine the TERM5 expressions.

<math>~\mathrm{Re}\biggl[\mathrm{TERM5}\biggr]</math>	<math>~=</math>	<math>~ \mathrm{Re}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Re}[ 2^3(n+1)^2 + 2m^2\Lambda ] -\mathrm{Im}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Im}[ 2^3(n+1)^2 + 2m^2\Lambda ] </math>
Case B:	<math>~=</math>	<math>~ \biggl\{ \ell^4\biggl[1-\frac{3\beta^2}{2(n+1)}\biggr] + 2\ell^2\biggl(-1\biggr)+ 1 \biggr\} \cdot \biggl\{ 2^3(n+1)^2 + 2m^2\biggl[ ~- (4n+1)\beta^2 + (n+1)^2(2^3 \cos^2\theta - 3) x^2(1+xb)\biggr] \biggr\} </math>
		<math>~ -~\biggl\{ \ell^4(-1)\biggl[\frac{2\cdot 3\beta^2}{(n+1)}\biggr]^{1/2} + 2\ell^2\biggl[ \frac{3\beta^2}{2(n+1)}\biggr]^{1/2} \biggr\} \cdot 2m^2\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot x(1+xb)^{1/2} </math>
	<math>~=</math>	<math>~ \biggl\{1 - 2\ell^2 + \ell^4-\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot \biggl\{ \biggl[ 2^3(n+1)^2 - 2m^2(4n+1)\beta^2\biggr] + x^2\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr\} </math>
		<math>~ -~x\beta^2 \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} </math>
	<math>~=</math>	<math>~ \biggl\{1 - 2\biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] + \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \biggr] </math>
		<math>~ -\frac{3\beta^2}{2(n+1)} \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] \biggr\} </math>
		<math>~\times \biggl\{ \biggl[ 2^3(n+1)^2 - 2m^2(4n+1)\beta^2\biggr] + \beta^2 \biggl( \frac{x}{\beta}\biggr)^2\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) + \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} </math>
		<math>~ -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math>
		<math>~ \times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] </math>
	<math>~=</math>	<math>~ \biggl\{\beta^0(1-2+1) + (4-4)\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + (6-2)\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta </math>
		<math>~ -\frac{3\beta^2}{2(n+1)} \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] \biggr\} </math>
		<math>~\times \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggl[- (4n+1) + \biggl( \frac{x}{\beta}\biggr)^2 (n+1)^2(2^3 \cos^2\theta - 3) \biggr] + \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} </math>
		<math>~ -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math>
		<math>~ \times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] </math>
	<math>~\approx</math>	<math>~ \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta +\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta + \mathcal{O}(\beta^4) \biggr\} </math>
		<math>~\times \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggl[- (4n+1) + \biggl( \frac{x}{\beta}\biggr)^2 (n+1)^2(2^3 \cos^2\theta - 3) \biggr] + \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} </math>
		<math>~ -~\beta^4\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ 2 \biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math>
		<math>~ \times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] </math>
	<math>~\approx</math>	<math>~2^3(n+1)^2 \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta +\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta + \mathcal{O}(\beta^4) \biggr\} \, . </math>

Sum of TERM$ and TERM5

When added together, we obtain,

<math>~\mathrm{Re}[\mathrm{TERM4} + \mathrm{TERM5}]</math>	<math>~=</math>	<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \ell^4\cdot 2^2 (n+1)[2^3(n+1)\cos^2\theta -3 ]\biggl(1+\frac{3xb}{2}\biggr)^2 </math>
		<math>~ -~ \beta^3 \biggl(\frac{x}{\beta}\biggr)^3\ell^4\cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) ~-~\beta^4\biggl(\frac{x}{\beta}\biggr)^4 \ell^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta-3] </math>
		<math>~ +~\biggl\{1 - 2\ell^2 + \ell^4 \biggr\} \cdot \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggr[ - (4n+1) + \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr]\biggr\} </math>
		<math>~ -~\frac{3\beta^2\ell^4}{2(n+1)} \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggr[ - (4n+1) + \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr]\biggr\} </math>
		<math>~ -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} </math>
	<math>~=</math>	<math>~ \beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2\ell^2 + \ell^4 \biggr\} </math>
		<math>~ -~\beta^2 \cdot 2m^2 [ 1 - 2\ell^2 + \ell^4 ] \cdot \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] </math>
		<math>~ -~\beta^2\ell^4 2^2\cdot 3 (n+1) + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \ell^4\cdot 2^2 (n+1)[3 - 2^3(n+1)\cos^2\theta ]\biggl(1+\frac{3xb}{2}\biggr)^2 </math>
		<math>~ -~\cancelto{0}{\beta^3}\biggl(\frac{x}{\beta}\biggr) \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} </math>
		<math>~ -~ \cancelto{0}{\beta^3} \biggl(\frac{x}{\beta}\biggr)^3\ell^4\cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) ~-~\cancelto{0}{\beta^4}\biggl(\frac{x}{\beta}\biggr)^4 \ell^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta-3] </math>
		<math>~ +~\frac{3\cancelto{0}{\beta^4}\ell^4 m^2}{(n+1)} \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] </math>
	<math>~\approx</math>	<math>~ \beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2\biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] + \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)} \biggr] \biggr\} </math>
		<math>~ -~\beta^2 \cdot 2m^2 [ 1 - 2 + 1 ] \cdot \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+\cancelto{0}{x}b) \biggr] </math>
		<math>~ -~\beta^2 2^2\cdot 3 (n+1) + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 2^2 (n+1)[3 - 2^3(n+1)\cos^2\theta ]\biggl(1+\frac{3\cancelto{0}{x}b}{2}\biggr)^2 </math>
	<math>~\approx</math>	<math>~ \beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2+ 1 \biggr\} +~\beta^1 \biggl(\frac{x}{\beta}\biggr) \cdot 2^3(n+1)^2\biggl\{4\cos\theta -4\cos\theta \biggr\} </math>
		<math>~ +~\beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \cdot 2^5(n+1)^2 \cos^2\theta </math>
		<math>~ -~\beta^2 \cdot 2m^2 [ 1 - 2 + 1 ] \cdot \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) \biggr] </math>
		<math>~ -~\beta^2 2^2\cdot 3 (n+1) \biggl[1 - \biggl(\frac{x}{\beta}\biggr)^2\biggr] - \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta ] </math>
	<math>~=</math>	<math>~-~\beta^2 2^2\cdot 3 (n+1) \biggl[1 - \biggl(\frac{x}{\beta}\biggr)^2\biggr] \, .</math>

So we see that the coefficients of the lowest-order <math>(\beta^0 ~\mathrm{and} ~ \beta^1)</math> terms are zero, and the coefficient of the <math>~\beta^2</math> term is almost zero! My analysis the second time around gives,

<math>~\Rightarrow ~~~ \mathrm{Re}\biggl[\mathrm{TERM4} + \mathrm{TERM5}\biggr]</math>	<math>~\approx</math>	<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] -~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b </math>
		<math>~ -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta +~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^4 (n+1)[2^3(n+1)\cos^2\theta -3] \cos\theta </math>
		<math>~+2^3(n+1)^2 \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta +\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr\} </math>
	<math>~\approx</math>	<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta] +~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2\cdot 3 (n+1) </math>
		<math>~+2^3(n+1)^2 \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} \biggr\} </math>
	<math>~=</math>	<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta] +~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2\cdot 3 (n+1) </math>
		<math>~+ \beta^2\biggl(\frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta ] -\beta^22^2\cdot 3(n+1) </math>
	<math>~=</math>	<math>~ -\beta^22^2\cdot 3(n+1)\biggl[1-\biggl( \frac{x}{\beta}\biggr)^2 \biggr] \, . </math>

Exactly the same as the first time around.

Imaginary Parts

TERM1

<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM1}}{\ell^2}\biggr]</math>	<math>~=</math>	<math>~ \beta\cos\theta [2^3\cdot 3(n+1)^3]^{1/2} \biggl[ \frac{b(4+3xb)}{(1+xb)^{3/2}} \biggr] </math>
		<math>~ +\frac{1}{x^2} \cdot (-1)\beta [2^7\cdot 3 (n+1)^3 ]^{1/2} \biggl\{ (\beta\eta)\cos\theta + \frac{3x^3\sin^2\theta}{2(\beta\eta)}(5\cos^2\theta -2) + \frac{3^2x^6\sin^6\theta\cos\theta}{2^2(\beta\eta)^3} \biggr\} </math>

TERM2

<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM2}}{\ell^2}\biggr]</math>	<math>~=</math>	<math>~\beta~\biggl[ \frac{2^5\cdot 3 (n+1)^3}{1+x(3\cos\theta-\cos^3\theta)} \biggr]^{1/2} \biggl\{ 2\cos\theta - x[2 - 7\cos^2\theta + 3\cos^4\theta ] </math>
		<math>~- x^2 \cos\theta [ 9 +4\cos^2\theta -\cos^4\theta ] \biggr\}</math>

TERM4

<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math>	<math>~=</math>	<math>~ \biggl\{ \beta\cos\theta [2^5\cdot 3 (n+1)^3]^{1/2} \cdot \frac{x(2+3xb)}{(\beta\eta)}\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] </math>
		<math>~ -~ \beta \sin\theta [2^7\cdot 3 (n+1)^3 (\beta\eta)^2]^{1/2}\biggl\{ 1 +\frac{3x^3}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(\beta\eta)^2} \biggr]\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] </math>
	<math>~=</math>	<math>~ -~x \cdot 2\beta\cos\theta [2^7\cdot 3 (n+1)^3]^{1/2} \cdot (1+xb)^{-1/2}\cdot \biggl(1+\frac{3xb}{2}\biggr)^2 </math>
		<math>~ -~ x^2\cdot 3\beta \sin^4\theta [2^7\cdot 3 (n+1)^3 ]^{1/2} (1+xb)^{1/2} \biggl\{ 1 +\frac{3x}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(1+xb)} \biggr]\biggr\} </math>
	<math>~=</math>	<math>~ -x\biggl\{~[~109.8335164~] + x[~119.7674436~]~\biggr\}= -34.94384433 </math>

Alternatively we can write,

<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math>	<math>~=</math>	<math>~ \biggl\{ \beta\cos\theta [2^5\cdot 3 (n+1)^3]^{1/2} \cdot \frac{x(2+3xb)}{(\beta\eta)}\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] </math>
		<math>~ -~ \beta \sin\theta [2^7\cdot 3 (n+1)^3 (\beta\eta)^2]^{1/2}\biggl\{ 1 +\frac{3x^3}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(\beta\eta)^2} \biggr]\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] </math>
	<math>~=</math>	<math>~ -2b_0 \beta^2 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} -~ 3b_0\beta^3 \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} </math>
		<math>~ -~ \frac{9b_0}{2} \cdot \beta^4 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} </math>

<math>~\Rightarrow ~~~ \mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\beta^2}\biggr]</math>	<math>~=</math>	<math>~\biggl\{ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} -~ 3b_0\beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} -~ \frac{9b_0}{2} \cdot \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} \biggr\} </math>
		<math>~ \times \biggl\{ 1 -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \biggr\} </math>
<math>~</math>	<math>~=</math>	<math>~ \biggl\{ ~-27.45837910~-6.77631589 ~-0.70914934~ \biggr\}\times [~0.58618164~] =\biggl\{ ~-34.94384433~ \biggr\}\times [~0.58618164~] = -20.48343998 </math>
	<math>~\approx</math>	<math>~ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} -~ 3b_0\beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} -~ \frac{9b_0}{2} \cdot \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} </math>
		<math>~+~ 8b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos\theta +~ 12b_0\beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \cos\theta </math>
		<math>~ -12b_0 \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos^2\theta </math>
	<math>~\approx</math>	<math>~ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} +~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8\biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \biggr\} </math>
		<math>~+\beta^2 b_0\biggl(\frac{x}{\beta}\biggr)^3\biggl\{ -~ \frac{9}{2} \cdot \sin^6\theta (1 + xb)^{-1/2} +~ 12 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \cos\theta -12 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos^2\theta \biggr\} </math>
	<math>~\approx</math>	<math>~ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} +~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} \, . </math>

TERM5

<math>~\mathrm{Im}\biggl[\mathrm{TERM5}\biggr]</math>	<math>~=</math>	<math>~ \mathrm{Re}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Im}[ 2^3(n+1)^2 + 2m^2\Lambda ] +\mathrm{Im}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Re}[ 2^3(n+1)^2 + 2m^2\Lambda ] </math>
Case B:	<math>~=</math>	<math>~ x\cdot 2 \beta m^2 \biggl\{1 - 2\ell^2 + \ell^4 -\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} </math>
		<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} [\ell^2 -\ell^4] \cdot \biggl\{ \biggl[ 2^3(n+1)^2 ~- 2m^2(4n+1)\beta^2\biggr] + x^2 \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] (1+xb) \biggr\} </math>
	<math>~=</math>	<math>~ \cancelto{1}{m^2} \biggl\{1 - 2\ell^2 + \ell^4 -\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot 2 \beta x[ ~ 32.12475681~] +~\sqrt{3}\beta [\ell^2 -\ell^4] \cdot \biggl\{ \biggl[ 2^5 ~- 10\cancelto{1}{m^2}\beta^2\biggr] + 2m^2x^2 \cdot [ ~2.6875~ ] \biggr\} </math>
	<math>~=</math>	<math>~ \cancelto{1}{m^2} \biggl\{~-0.38470459~\biggr\} \cdot [ ~16.06237841~] +~[~0.31080502~] \cdot \biggl\{ 22.3359375\biggr\}= 0.76285080 \, . </math>

Let's rewrite both of these expressions in terms of a power series in <math>~\beta</math>.

<math>~\mathrm{Im}\biggl[\mathrm{TERM5}\biggr]</math>	<math>~=</math>	<math>~ \beta^2\biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 \biggl\{1 - 2\biggl[1 -2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math>
		<math>~ + \biggl[1 -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr]\biggl[1 -\frac{3\beta^2}{2(n+1)} \biggr]\biggr\} \cdot \biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \mathcal{O}(\beta^3)\biggr\} </math>
		<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ 2^3(n+1)^2 \biggr\} </math>
		<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ ~- 2m^2(4n+1)\beta^2 \biggr\} </math>
		<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ x^2 \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] \biggr\} </math>
		<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ x^3 b \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] \biggr\} </math>

<math>~\Rightarrow~~~\mathrm{Im}\biggl[\frac{\mathrm{TERM5}}{\beta^2}\biggr]</math>	<math>~=</math>	<math>~ \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 \biggl\{\beta^0(1-2+1) +4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta -2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} + \mathcal{O}(\beta^3) \biggr\} </math>
		<math>~ \times \biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \mathcal{O}(\beta^3)\biggr\} </math>
		<math>~ +~b_0\biggl[ \frac{(1-1)}{\beta\cos\theta} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta +4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta + \mathcal{O}(\beta^3)\biggr] </math>
		<math>~ -~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^{1}(1-1) + 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^3 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^4 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^5)\biggr] </math>
		<math>~ +~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^1\biggl( \frac{x}{\beta}\biggr)^2(1-1) + 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta - 5\beta^3\biggl( \frac{x}{\beta}\biggr)^4 \cos^2\theta +4\beta^4\biggl( \frac{x}{\beta}\biggr)^5\cos^3\theta + \mathcal{O}(\beta^3)\biggr] </math>
		<math>~ +~m^2 b [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^2\biggl(\frac{x}{\beta}\biggr)^3 (1-1) + 2\beta^3\biggl(\frac{x}{\beta}\biggr)^4 \cos\theta - 5\beta^4\biggl(\frac{x}{\beta}\biggr)^5 \cos^2\theta +4\beta^5\biggl(\frac{x}{\beta}\biggr)^6 \cos^3\theta + \mathcal{O}(\beta^3)\biggr] </math>

Dropping all terms on the right-hand-side that are <math>~\mathcal{O}(\beta^3)</math> or higher, we have,

<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM5}}{\beta^2}\biggr]</math>	<math>~=</math>	<math>~ \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 \biggl\{\beta^0(1-2+1) +(4-4)\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta +4 \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - \beta^2\biggl[ \frac{3}{2(n+1)}\biggr] + \cancelto{0}{\mathcal{O}(\beta^3)} \biggr\} </math>
		<math>~ \times \biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr\} </math>
		<math>~ +~b_0\biggl[ \frac{(1-1)}{\beta\cos\theta} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta +4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math>
		<math>~ -~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^{1}(1-1) + 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math>
		<math>~ +~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^1\biggl( \frac{x}{\beta}\biggr)^2(1-1) + 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math>
		<math>~ +~m^2 b [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^2\biggl(\frac{x}{\beta}\biggr)^3 (1-1) + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math>
	<math>~\approx</math>	<math>~m^2 b_0 \biggl\{- \biggl[ \frac{3}{(n+1)}\biggr]\biggl(\frac{x}{\beta}\biggr) + 8 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta \biggr\} \times\biggl\{ \beta^2 +\cancelto{0}{\mathcal{O}(\beta^3)} \biggr\} </math>
		<math>~ +~b_0\biggl[ 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta + 4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta \biggr] </math>
		<math>~ -~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr] </math>
		<math>~ +~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta \biggr] </math>
	<math>~\approx</math>	<math>~2b_0\beta^0\biggl(\frac{x}{\beta}\biggr) - 5b_0\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta + 4b_0\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta </math>
		<math>~+\beta^2 m^2 \biggl\{- \biggl[ \frac{3b_0}{(n+1)}\biggr]\biggl(\frac{x}{\beta}\biggr) + 8 b_0\biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta -~ (4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ 2\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr] +~ [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ 2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta \biggr] \biggr\} \, . </math>

Together

Together, then, we have:

<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}+\mathrm{TERM5}}{b_0\beta^2}\biggr]</math>	<math>~\approx</math>	<math>~ -2\biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} + \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta </math>
	<math>~\approx</math>	<math>~ -2\biggl(\frac{x}{\beta}\biggr) \biggl(1+3xb \biggr) \biggl(1- \frac{xb}{2} \biggr) + 2\biggl(\frac{x}{\beta}\biggr) + \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 3 \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} </math>
	<math>~\approx</math>	<math>~ -\biggl(\frac{x}{\beta}\biggr) \biggl[2+5bx \biggr] + 2\biggl(\frac{x}{\beta}\biggr) + \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ \cos^2\theta -\sin^4\theta \biggr\} </math>
	<math>~=</math>	<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) -5\beta\biggl(\frac{x}{\beta}\biggr)^2 [3\cos\theta - \cos^3\theta] + \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ \cos^2\theta -[1-2\cos^2\theta + \cos^4\theta] \biggr\} </math>
	<math>~=</math>	<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) -\frac{5\beta}{\cos\theta}\biggl(\frac{x}{\beta}\biggr)^2 [3\cos^2\theta - \cos^4\theta] + \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ -1+3\cos^2\theta - \cos^4\theta \biggr\} </math>
	<math>~=</math>	<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) + \frac{\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ -3+9\cos^2\theta - 3\cos^4\theta -15\cos^2\theta + 5\cos^4\theta \biggr\} </math>
	<math>~=</math>	<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) - \frac{\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 3 + 6\cos^2\theta - 2\cos^4\theta \biggr\} </math>

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |

When added together, we obtain,

<math>~\mathrm{Im}[\mathrm{TERM4} + \mathrm{TERM5}]</math>	<math>~=</math>	<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr) \ell^4 \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} \cdot (1+xb)^{-1/2}\cdot \biggl(1+\frac{3xb}{2}\biggr)^2 </math>
		<math>~ -~\cancelto{0}{\beta^3} \biggl(\frac{x}{\beta}\biggr)^2\cdot 3 \ell^4 \sin^4\theta [2^7\cdot 3 (n+1)^3 ]^{1/2} (1+xb)^{1/2} \biggl\{ 1 +\frac{3x}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(1+xb)} \biggr]\biggr\} </math>
		<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2\ell^2 + \ell^4 ] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} </math>
		<math>~-\cancelto{0}{\beta^4} \biggl(\frac{x}{\beta}\biggr) \biggl[\frac{3 m^2\ell^4}{(n+1)} \biggr] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} </math>
		<math>~ -~\beta [ 2^7\cdot 3 (n+1)^3]^{1/2} [\ell^2 -\ell^4] </math>
		<math>~ +~\cancelto{0}{\beta^3} \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} [\ell^2 -\ell^4] \cdot \biggl[ 2m^2(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2 2m^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] </math>
	<math>~\approx</math>	<math>~ -~\beta^1 [ 2^7\cdot 3 (n+1)^3]^{1/2} \biggl\{ \biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^2)} \biggr] - \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^2)} \biggr] \biggr\} </math>
		<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr) \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} \cdot (1+\cancelto{0}{x}b)^{-1/2}\cdot \biggl(1+\frac{3\cancelto{0}{x}b}{2}\biggr)^2 </math>
		<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+\cancelto{0}{x}b)^{1/2} </math>
	<math>~\approx</math>	<math>~ -~\beta^1 [ 2^7\cdot 3 (n+1)^3]^{1/2} [1 - 1] </math>
		<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr)\cos\theta [ 2^9\cdot 3 (n+1)^3]^{1/2} -~\beta^2 \biggl(\frac{x}{\beta}\biggr) \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} </math>
		<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta </math>

Summary

As stated above, the eigenvalue problem that must be solved in order to identify the eigenfunction, <math>~\Lambda(x,\theta)</math>, and eigenfrequency, <math>~(\nu/m)</math>, of unstable (as well as stable) nonaxisymmetric modes in slim <math>~(\beta \ll 1)</math>, polytropic <math>~(n)</math> PP tori with uniform specific angular momentum is defined by the following two-dimensional <math>~(x,\theta)</math>, 2^nd-order PDE:

<math>~f (1-x\cos\theta)^2 \biggl\{ ~\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3} \biggr\} + ~\frac{n}{\beta^2} \biggl\{ \mathrm{TERM4} ~+~ \mathrm{TERM5}\biggr\} \, , </math>

where, <math>~f(x,\theta)</math> is the enthalpy distribution in the unperturbed, axisymmetric torus, and

<math>~\mathrm{TERM1}</math>	<math>~\equiv</math>	<math>~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] \, ,</math>
<math>~\mathrm{TERM2}</math>	<math>~\equiv</math>	<math>~\frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] \, ,</math>
<math>~\mathrm{TERM3}</math>	<math>~\equiv</math>	<math>~- [ 2^2(n+1)^2 + m^2\Lambda ] \, ,</math>
<math>~\mathrm{TERM4}</math>	<math>~\equiv</math>	<math>~(1-x\cos\theta)^4\biggl[ \frac{\partial \Lambda}{\partial x} \cdot \frac{\partial (\beta^2 f)}{\partial x} ~+~ \frac{\partial \Lambda}{\partial \theta} \cdot \frac{\partial (\beta^2 f/x^2)}{\partial \theta} \biggr] \, ,</math>
<math>~\mathrm{TERM5}</math>	<math>~\equiv</math>	<math>~\biggl[ (1-x\cos\theta)^4\biggl(\frac{\nu}{m}\biggr)^2 + 2(1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] [ 2^3(n+1)^2 + 2m^2\Lambda ] \, .</math>

If an exact solution, <math>~(\Lambda,\nu/m)</math>, to this eigenvalue problem were plugged into this governing PDE, we would expect that both of the following summations would be exactly zero at all meridional-plane <math>~(x,\theta)</math> locations throughout the torus:

<math>~0</math>	<math>~=</math>	<math>~\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3} \, ,</math>
<math>~0</math>	<math>~=</math>	<math>~\mathrm{TERM4} + \mathrm{TERM5} \, .</math>

While an exact analytic solution to this eigenvalue problem is not (yet) known, Blaes (1985) has determined that a good approximate solution is an eigenvector defined by the complex eigenfrequency,

<math> ~-1 ~\pm ~ i~\biggl[ \frac{3}{2(n+1)} \biggr]^{1/2} \beta \, , </math>

and, simultaneously, the complex eigenfunction,

<math>~\Lambda</math>

<math>~- (4n+1)\beta^2 + (\beta\eta)^2 (n+1)^2[ 2^3 \cos^2\theta - 3] ~\pm~i~\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta \, , </math>

where,

<math>~x^2[1+x(3\cos\theta - \cos^3\theta )] \, .</math>

We have plugged this "Blaes85" approximate eigenvector into the five separate "TERM" expressions — analytically evaluating partial (1^st and 2^nd) derivatives along the way, as appropriate — then, with the aid of an Excel spreadsheet, have numerically evaluated each of the expressions over a range of coordinate locations <math>~(0 < x/\beta < 1; 0 \le \theta \le 2\pi)</math>. The appropriate numerical sums of these TERMs are, indeed, nearly zero for slim <math>~(\beta \ll 1)</math> configurations.

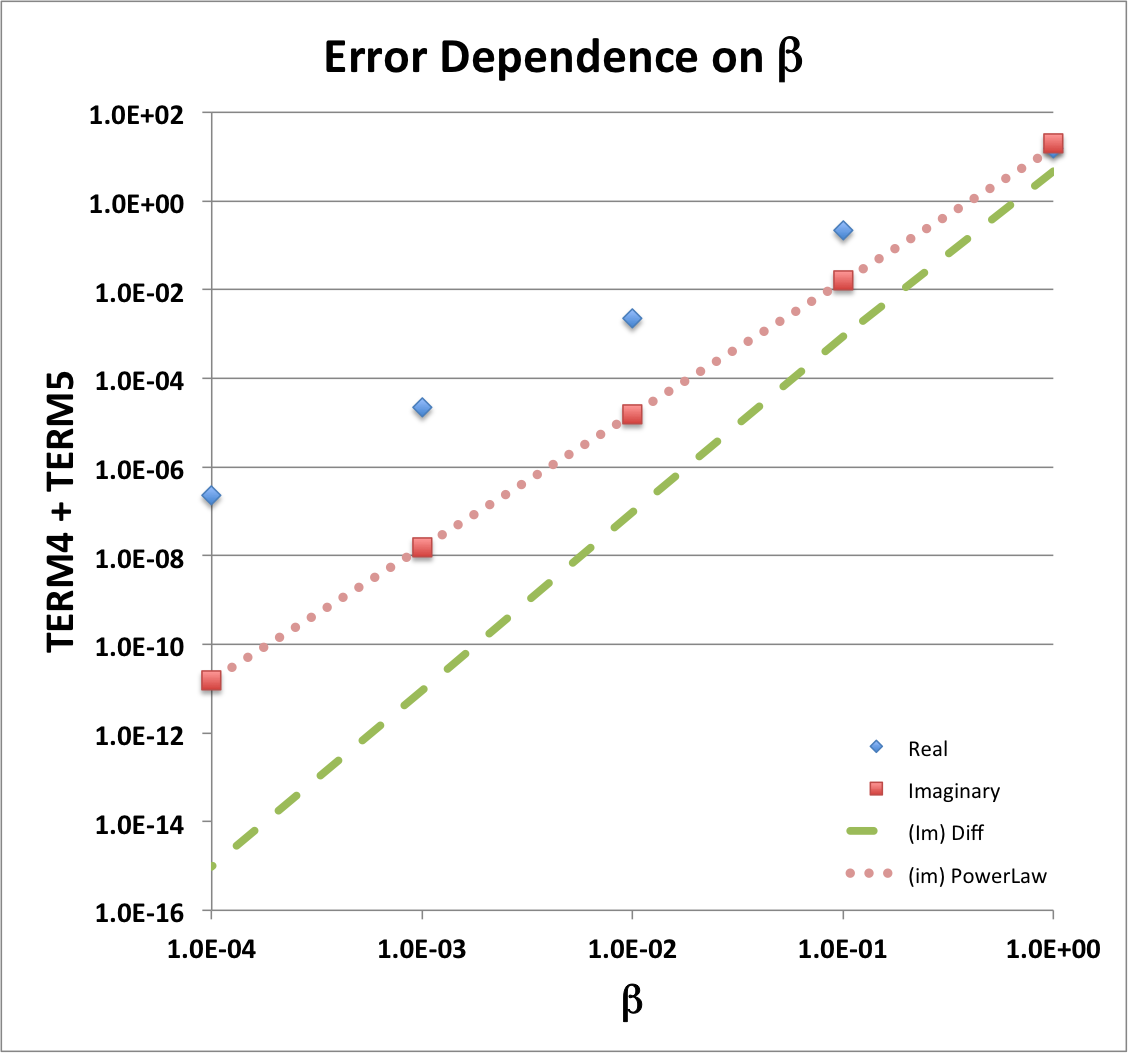
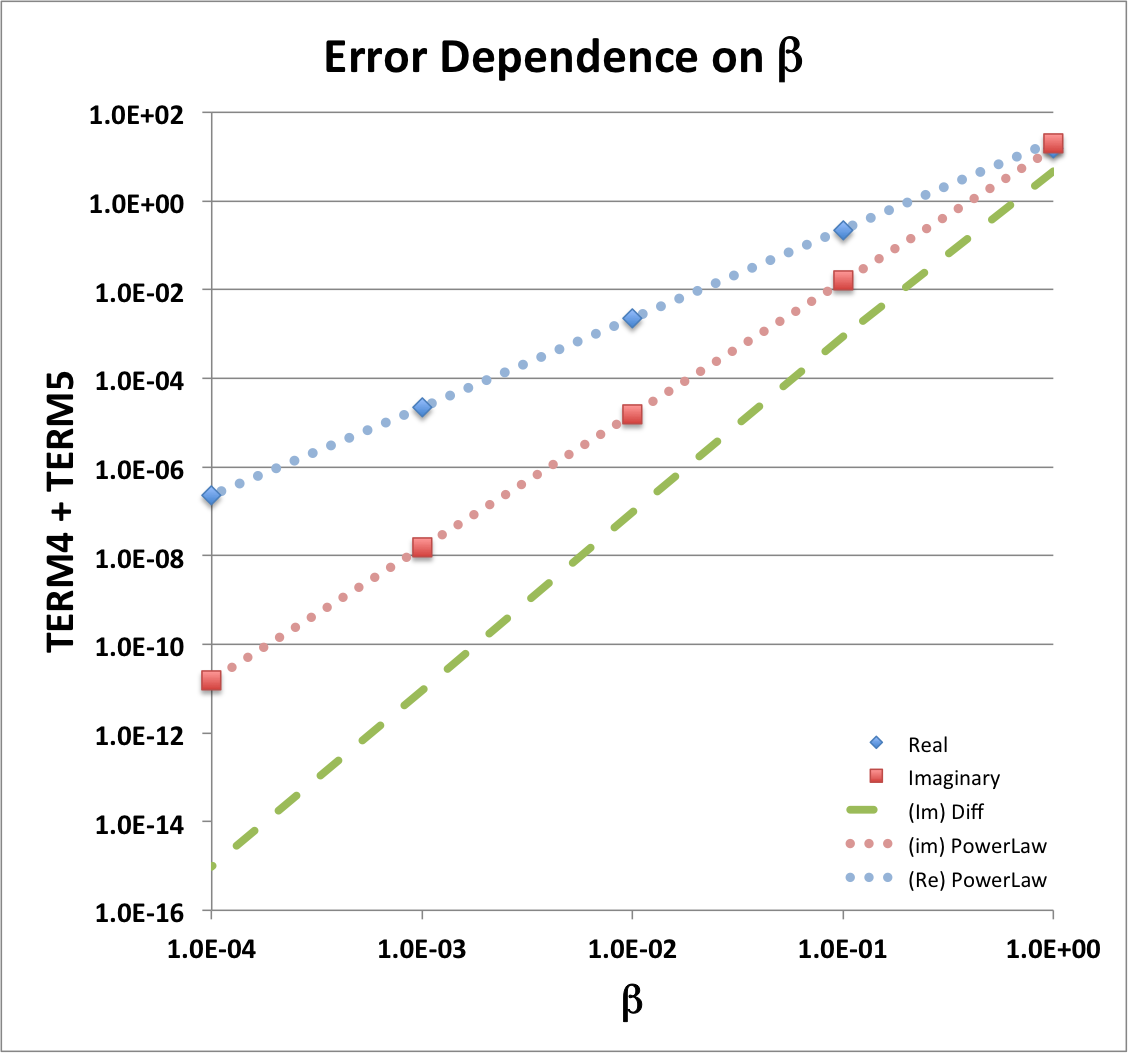
The log-log plot shown here, on the right, illustrates the behavior of the "TERM4 + TERM5" sum for the example parameter set, <math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math>. As the blue diamonds illustrate, the real part of this sum drops by approximately two orders of magnitude for every factor of ten drop in <math>~\beta</math>. The total drop is roughly eight orders of magnitude over the displayed range, <math>~\beta = 1 ~\rightarrow~ 10^{-4}</math>. As the salmon-colored squares in the same plot indicate, the imaginary part of the sum, "TERM4 + TERM5," is even closer to zero, dropping roughly 12 orders of magnitude over the same range of <math>~\beta</math>. This indicates that, with the Blaes85 eigenvector, the real part of the sum of this pair of terms differs from zero by a residual whose leading-order term varies as <math>~\beta^{2}</math> while the corresponding imaginary part of the sum differs from zero by a residual whose leading-order term varies as <math>~\beta^{3}</math>.

As our above analytic analysis shows, when each of the expressions for TERM4 and TERM5 is rewritten as a power series in <math>~\beta</math>, a sum of the two analytically specified TERMs results in precise cancellation of leading-order terms. For the imaginary component of this sum, our derived expression for the residual is,

<math>~\mathrm{Im}(\mathcal{R}_{45})</math>	<math>~\equiv</math>	<math>~\mathrm{Im}[\mathrm{TERM4}+\mathrm{TERM5}]</math>
	<math>~=</math>	<math>~ - \beta^3 \biggl(\frac{x}{\beta}\biggr)^2 [2^7\cdot 3 (n+1)^3]^{1/2}[ 3 + 6\cos^2\theta - 2\cos^4\theta ] + \mathcal{O}(\beta^4) \, . </math>

The dotted, salmon-colored line of slope 3 that has been drawn in our accompanying log-log plot was generated using this analytic expression for the <math>~\beta^3</math>-residual term. It appears to precisely thread through the points (the salmon-colored squares) whose plot locations have been determined via our numerical spreadsheet evaluation of the imaginary component of the "TERM4 + TERM5" sum. Additional confirmation that we have derived the correct analytic expression for <math>~\mathrm{Im}(\mathcal{R}_{45})</math> comes from subtracting this analytically defined <math>~\beta^3</math> residual from the numerically determined sum: The result is the green-dashed curve in the accompanying log-log plot, which appears to be a line of slope 4.

Analogously, for the real component of this sum, the precise expression for the residual is,

<math>~\mathrm{Re}(\mathcal{R}_{45})</math>	<math>~\equiv</math>	<math>~\mathrm{Re}[\mathrm{TERM4}+\mathrm{TERM5}]</math>
	<math>~=</math>	<math>~ -\beta^22^2\cdot 3(n+1)\biggl[1-\biggl( \frac{x}{\beta}\biggr)^2 \biggr] + \mathcal{O}(\beta^3) \, . </math>

The dotted, light blue line of slope 2 that has been drawn in our accompanying log-log plot was generated using this analytic expression for the <math>~\beta^2</math>-residual term. It appears to precisely thread through the points (the light blue diamonds) whose plot locations have been determined via our numerical spreadsheet evaluation of the real part of the "TERM4 + TERM5" sum. Notice that at the surface of the torus — that is, when <math>~x/\beta = 1</math> — this <math>~\beta^2</math>-residual goes to zero, in which case the leading order term in the "real" component residual will be drop to <math>~\mathcal{O}(\beta^3)</math>.

User:Tohline/Appendix/Ramblings/PPToriPt2

Contents

Stability Analyses of PP Tori (Part 2)

Start From Scratch

Basic Equations from Blaes85

Our Manipulation of These Equations

Analytic

Example Evaluation

Testing for Expected Cancellations

Real Parts

TERM1

TERM2

TERM4

TERM5

Sum of TERM$ and TERM5

Imaginary Parts

TERM1

TERM2

TERM4

TERM5

Together

Summary

See Also

Navigation menu

Search