User:Tohline/Apps/MaclaurinSpheroids/GoogleBooks
Excerpts from A Treatise of Fluxions
|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Both Volume I and Volume II of Colin Maclaurin's "A Treatise of Fluxions" can now be accessed online via Google Books. (Check out Wolfram's explanation of the term, fluxion.) In what follows, we provide an abbreviated table of contents for both volumes and present selected excerpts from these volumes.
|
Title Pages with Google-Books Links |
Example Digitized Figure Plate |
|
|---|---|---|
 |
 |
 |
|
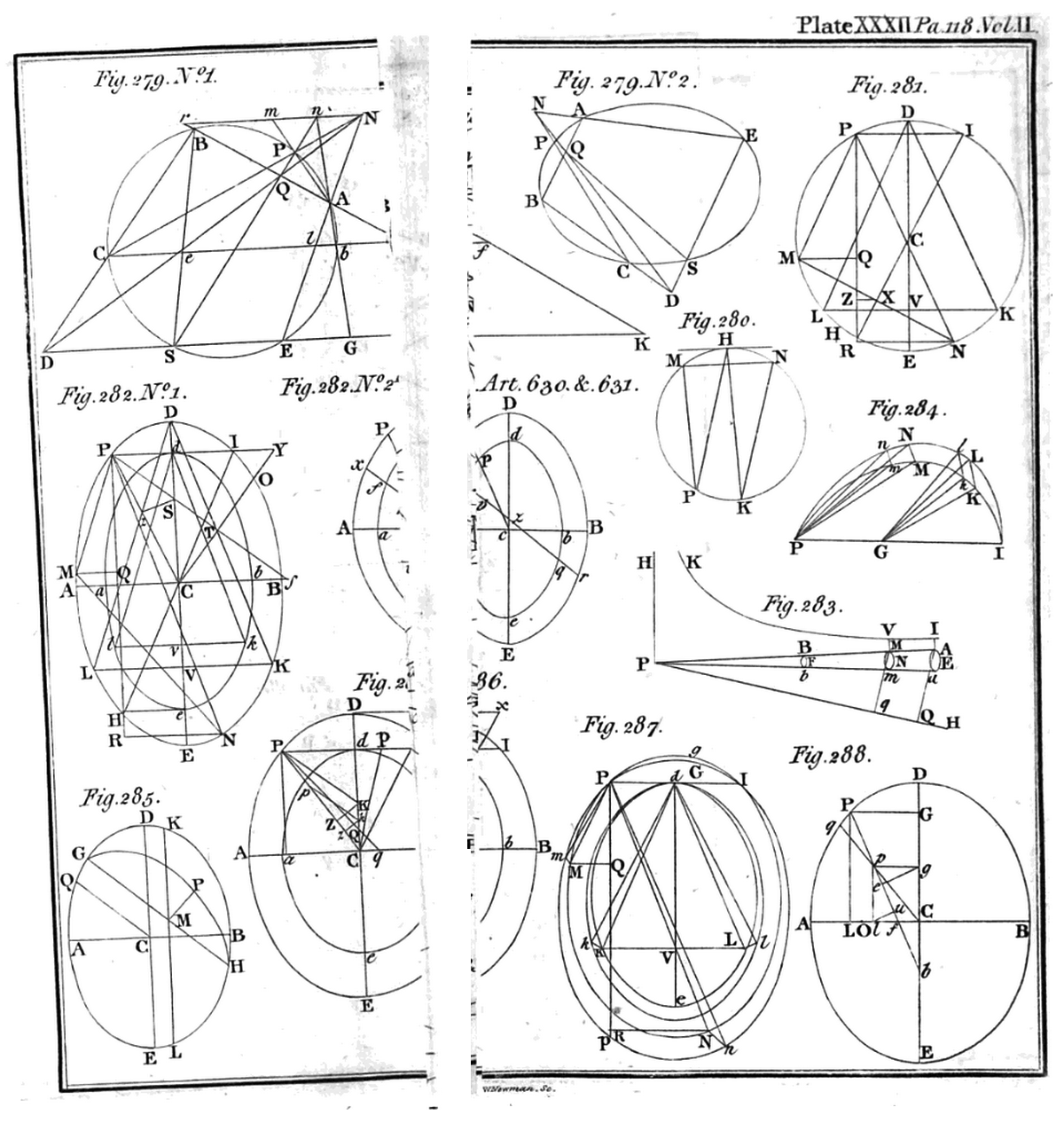
Plate XXXII |
||
As is illustrated in the righthand panel of the above image trio (click in the panel in order to view a higher-resolution image), each published "Figure Plate" was digitized (by Google Books) in segments that must be digitally pieced together in order to reconstruct some of the individual figures. See, for example, the discussion that references Fig. 282, below.
Volume I
| Dedication (an 18th Century Acknowledgment) | |
| Preface | |
| Introduction | 1 |
| Book 1 (Of the Fluxions of Geometrical Magnitudes) | 51 |
| Chapter I (Of the Grounds of this Method) — §§ 1-77 | 51 |
| Chapter II (Of the Fluxions of plane rectilineal Figures) — §§ 78-104 | 109 |
| Chapter III (Of the Fluxions of plane curvilineal Figures) — §§ 105-123 | 131 |
| Chapter IV (Of the Fluxions of Solids, and of third Fluxions) — §§ 124-139 | 142 |
| Chapter V (Of the Fluxions of Quantities that are in a continued Geometrical Progression, the first term of which is invariable) — §§ 140-150 | 152 |
| Chapter VI (Of Logarithms, and of the Fluxions of logarithmic Quantities) — §§ 151-179 | 158 |
| Chapter VII (Of the Tangents of curve Lines) — §§ 180-214 | 178 |
| Chapter VIII (Of the Fluxions of curve Surfaces) — §§ 215-237 | 199 |
| Chapter IX ([Identifying Extrema and Inflection Points] of Curves that are defined by a common or by a fluxional Equation) — §§ 238-285 | 214 |
| Chapter X (Of the Asymptotes of curve Lines, the Areas bounded by them and …) — §§ 286-362 | 240 |
| Chapter XI (Of the Curvature of Lines … different kinds of Contact [with other Curves] … Caustics … centripetal Forces …) — §§ 363- | 304 |
| · Parabola — §371 | 311 |
| · Any Conic Section — §373 | 312 |
| · The Second Fluxion of a Curve — §384 | 324 |
| · Refraction of Light — §413 | 344 |
| · Centripetal and Centrifugal Forces — §416 | 346 |
| · Gravity — §419 | 348 |
| · Circular Motion — §432 | 356 |
| · When the Center of Forces is the Focus of a Conic Section — §446 | 370 |
| · When Gravity is Uniform or Varies as any Power of the Distance — §458 | 383 |
| · Orbit of the Moon, taking into account the Gravity of both the Earth and the Sun — §471 | 391 |
 Extracted directly from §487 of Maclaurin's Book 1, as digitized by Google |
|
| · Prolate Spheroidal Fluid Figure — §491 | 409 |
 Extracted directly from §491 of Maclaurin's Book 1, as digitized by Google |
|
| · The Earth's Equilibrium Shape — §492 | 410 |
 Extracted directly from §492 of Maclaurin's Book 1, as digitized by Google |
|
| End of Book I, Chapter XI, § 494 | 413 |
Volume II
| Table of Principal Contents (5 pp.) | |
| Figure Plates (30 pp.) | |
| Book 1 (continued) | 1 |
| Chapter XII (Of the Methods of Infinitesimals …) — §§ 495-570 | 1 |
| · Centre of Gravity — §510 | 13 |
| · Of the Collision of Bodies — §511 | 14 |
| · Of the Descent of Bodies that Act upon One Another — §521 | 27 |
| · Of the Centre of Oscillation — §533 | 40 |
| · Of the Motion of Water Issuing from a Cylindric Vessel — §537 | 44 |
| · Of the Catenaria — §551 | 59 |
| · General Observations Concerning the Angles of Contact, etc. — §554 | 61 |
| · General Observations Concerning centripetal Forces, etc. — §563 | 67 |
| Chapter XIII (Determining the Lines of swiftest Descent in any Hypothesis of Gravity …) — §§ 571-608 | 74 |
| · When Gravity is Directed Towards a Given Centre — §578 | 80 |
| · Isoperimetrical Problems — §588 | 88 |
| · The Solid of Least Resistance — §606 | 100 |
| Chapter XIV (Of the Ellipse Considered as the Section of a Cylinder … Of the Figure of the Earth …) — §§ 609- | 101 |
| · Properties of the Ellipse — §609 | 101 |
| · Of the Gravitation towards Spheres and Spheroids — §628 | 110 |
| · Of the Figures of Planets (including effects of rotation) — §636 | 116 |
| · Key Concluding Theorem! — §641 | 119 |
 |
|
| · Itemize Numerous Implications for Equilibrium Spheroids — §642 | 120 |
| · Apply Specifically to the Earth — §661 | 136 |
| · What if the Earth's Density isn't Uniform but, instead, Varies Linearly with Distance? — §670 | 143 |
| · Jupiter — §682 | 152 |
| · Tides — §686 | 154 |
| · Concluding Paragraph — §696 | 161 |
 |
|
| End of Book I | 162 |
Maclaurin's Discussion of Self-Gravitating, Oblate-Spheroidal Configurations
|
Paragraph (and related figure) extracted† from Colin Maclaurin (1742)
"A Treatise of Fluxions"
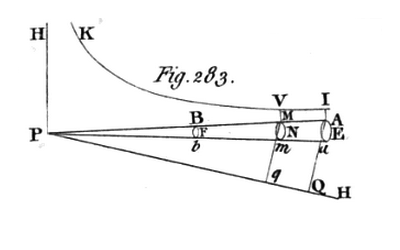
Volume II, Chapter XIV, §628 | |
 |
 |
 |
|
|
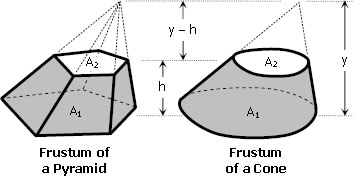
†As displayed here (left panel), this paragraph has been pieced together from two text segments found on separate but sequential pages (pp. 110-111) of Google's digitized volume. The diagram labeled Fig. 283 (top-right panel) has been extracted from Maclaurin's Figure Plate XXXIII, which appears near the beginning of the same digitized file, and has been displayed here without modification. The diagrams in the bottom-right panel have been reposted from Mathalino.com in an effort to illustrate what Maclaurin means by "frustum of a cone." |
|
|
Paragraph (and a pair of related diagrams) extracted† from Colin Maclaurin (1742)
"A Treatise of Fluxions"
Volume II, Chapter XIV, §630 | |
 |
 |
|
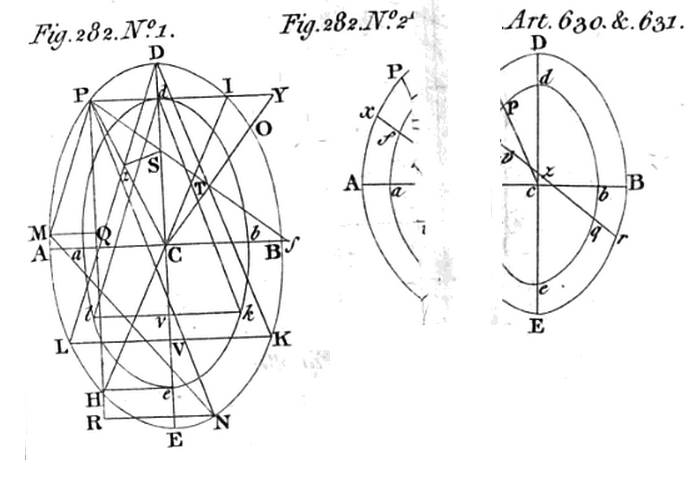
†The paragraph (left panel) has been extracted from p. 111 of Google's digitized volume and displayed here without modification. The pair of diagrams (right panel) has been extracted from Figure Plate XXXIII, which appears near the beginning of the same digitized file. Note that the diagram on the right has been (poorly) pieced together from segments that appear on two separate pages of Google's digitized volume, presumably because the figure plate, itself, is folded in the original print publication. |
|
Related Discussions
|
|
|---|
|
© 2014 - 2021 by Joel E. Tohline |