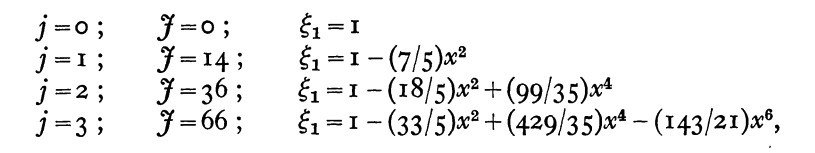Difference between revisions of "User:Tohline/SSC/UniformDensity"
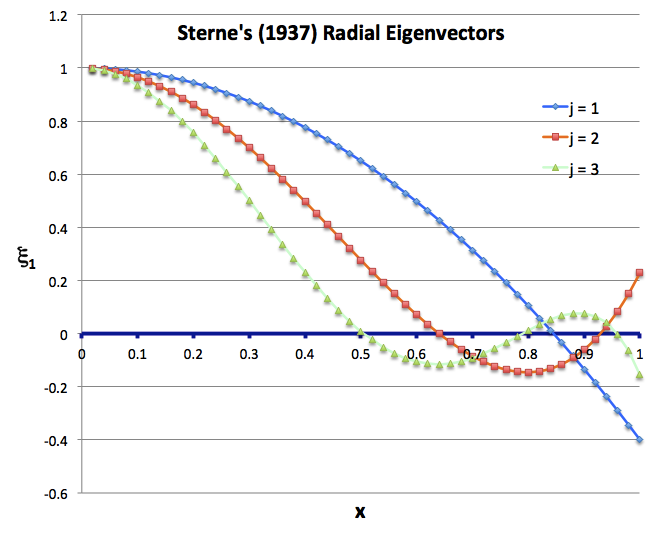
(→Sterne's General Solution: Insert Excel plot of Sterne's 3 eigenvectors) |
(→Stability: Explain dynamical instability) |
||
| Line 467: | Line 467: | ||
==Stability== | ==Stability== | ||
The [[User:Tohline/SSC/Perturbations#2ndOrderODE| | The [[User:Tohline/SSC/Perturbations#2ndOrderODE|Adiabatic Wave Equation]] that defines this [[User:Tohline/SSC/Perturbations#The_Eigenvalue_Problem|eigenvalue problem]] has been derived from the fundamental set of nonlinear [[User:Tohline/PGE#Principal_Governing_Equations|Principal Governing Equations]] by assuming that, for example, the radial position, <math>~r(m,t)</math>, at any time, <math>~t</math>, and of each mass shell throughout our spherical configuration can be described by the expression, | ||
<div align="center"> | <div align="center"> | ||
<math>~r(m,t) = r_0(m) [ 1 + x(m) e^{i\omega t} ] \, ,</math> | <math>~r(m,t) = r_0(m) [ 1 + x(m) e^{i\omega t} ] \, ,</math> | ||
</div> | </div> | ||
where, the fractional displacement, <math>~|x| \ll 1</math>. Switching to Sterne's variable notation, this should be written as, | |||
<div align="center"> | <div align="center"> | ||
<math>~\xi(x,t) = \xi_0(x) [ 1 + \xi_1(x) e^{i n t} ] \, ,</math> | <math>~\xi(x,t) = \xi_0(x) [ 1 + A\xi_1(x) e^{i n t} ] \, ,</math> | ||
</div> | </div> | ||
with the presumption that, <math>~| | with the presumption that the coefficient, <math>~|A| \ll 1</math>, and the understanding that, in Sterne's presentation, the variable, <math>~x</math>, is used to identify individual mass shells. Specifically, given <math>~R</math> and <math>~\bar\rho</math>, | ||
<div align="center"> | <div align="center"> | ||
<math>~m \equiv M_r = \frac{4}{3}\pi \xi_0^3 \bar\rho = \frac{4}{3}\pi (R x)^3 \bar\rho </math> | <math>~m \equiv M_r = \frac{4}{3}\pi \xi_0^3 \bar\rho = \frac{4}{3}\pi (R x)^3 \bar\rho </math> | ||
| Line 482: | Line 482: | ||
</div> | </div> | ||
Sterne's [[User:Tohline/SSC/UniformDensity#Sterne.27s_General_Solution|general solution of this eigenvalue problem]] describes mathematically how a self-gravitating, uniform-density configuration will vibrate if perturbed away from its equilibrium state; the oscillatory behavior associated with each pure radial mode, <math>~j</math> — among an infinite number of possible modes — is fully defined by the polynomial expression for the eigenvector, <math>~\xi_1(x)</math>, and the | Sterne's [[User:Tohline/SSC/UniformDensity#Sterne.27s_General_Solution|general solution of this eigenvalue problem]] describes mathematically how a self-gravitating, uniform-density configuration will vibrate if perturbed away from its equilibrium state; the oscillatory behavior associated with each pure radial mode, <math>~j</math> — among an infinite number of possible modes — is fully defined by the polynomial expression for the eigenvector, <math>~\xi_1(x)</math>, and the corresponding value of the square of the eigenfrequency, <math>~n^2</math>. | ||
If, for any mode, <math>~j</math>, the ''square'' of the derived eigenfrequency, <math>~n^2</math>, is positive, then the eigenfrequency itself will be a real number — specifically, | |||
<div align="center"> | |||
<math>~n = \pm \sqrt{|n^2|} \, .</math> | |||
</div> | |||
As a result, the radial location of every mass shell will vary sinusoidally in time according to the expression, | |||
<div align="center"> | |||
<math>~\frac{\xi(x,t)}{\xi_0} - 1 \propto e^{\pm i \sqrt{|n^2|} t} \, .</math> | |||
</div> | |||
If, on the other hand, <math>~n^2</math>, is negative, then the eigenfrequency will be an imaginary number — specifically, | |||
<div align="center"> | |||
<math>~n = \pm i \sqrt{|n^2|} \, .</math> | |||
</div> | |||
As a result, the radial location of every mass shell will grow (or damp) exponentially in time according to the expression, | |||
<div align="center"> | |||
<math>~\frac{\xi(x,t)}{\xi_0} - 1 \propto e^{\pm \sqrt{|n^2|} t} \, .</math> | |||
</div> | |||
This latter condition is the mark of a dynamically unstable system. It is in this manner that the solution to an eigenvalue problem can provide critical information regarding the relative stability of equilibrium configurations. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 04:24, 16 June 2015
The Stability of Uniform-Density Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
As far as we have been able to determine, T. E. Sterne (1937, MNRAS, 97, 582) was the first to use linearized perturbation techniques and, specifically, the Adiabatic Wave Equation, to thoroughly analyze the stability of uniform-density, self-gravitating spheres. While uniform-density configurations present an overly simplified description of real stars, Sterne's (1937) stability analysis is an important one because it presents a complete spectrum of radial pulsation eigenfunctions — eigenfrequencies plus the corresponding eigenvectors — as closed-form analytic expressions. Such analytic solutions are quite rare in the context of studies of the structure, stability, and dynamics of self-gravitating fluids.
As has been explained in an accompanying introductory discussion, this type of stability analysis requires the solution of an eigenvalue problem. Here we begin by re-presenting the governing 2nd-order ODE (the Adiabatic Wave Equation) as it was derived in the accompanying introductory discussion, along with the specification of two customarily used boundary conditions; and we review the properties of the equilibrium configuration — also derived in a separate discussion — that are relevant to this stability analysis. Interleaved with this presentation, we also show the governing wave equation as it was derived by Sterne (1937) — and a table that translates from Sterne's notation to ours — along with his corresponding review of the properties of the unperturbed equilibrium configuration. Finally, we present Sterne's (1937) solution to this eigenvalue problem and discuss the properties of his derived radial pulsation eigenfunctions.
The Eigenvalue Problem
Our Approach
As has been derived in an accompanying discussion, the second-order ODE that defines the relevant Eigenvalue problem is,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 .
</math>
where the dimensionless radius,
<math>
\chi_0 \equiv \frac{r_0}{R} ,
</math>
the characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) is,
<math>
\tau_\mathrm{SSC} \equiv \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} ,
</math>
and the characteristic gravitational acceleration is,
<math>
g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} .
</math>
The two boundary conditions are,
<math>~\frac{dx}{d\chi_0} = 0</math> at <math>~\chi_0 = 0 \, ;</math>
and,
|
<math>~ \frac{d\ln x}{d\chi_0}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) </math> at <math>~\chi_0 = 1 \, .</math> |
The Approach Taken by Sterne (1937)
T. E. Sterne (1937) begins his analysis by deriving the
Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
in a manner explicitly designed to reproduce Eddington's pulsation equation — it appears as equation (1.8) in Sterne's paper — and, along with it, the surface boundary condition,
|
<math>~ r_0 \frac{d\ln x}{dr_0}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) </math> at <math>~r_0 = R \, ,</math> |
which appears in Sterne's paper as equation (1.9). Then, as shown in the following paragraph extracted directly from his paper, Sterne (1937) rewrites both of these expressions in, what he considers to be, "more convenient forms."
|
Paragraph extracted from T. E. Sterne (1937)
"Modes of Radial Oscillation"
Monthly Notices of the Royal Astronomical Society, vol. 97, pp. 582 - © Royal Astronomical Society |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||
Properties of the Equilibrium Configuration
Our Setup
From our derived structure of a uniform-density sphere, in terms of the configuration's radius <math>R</math> and mass <math>M</math>, the central pressure and density are, respectively,
<math>P_c = \frac{3G}{8\pi}\biggl( \frac{M^2}{R^4} \biggr) </math> ,
and
<math>\rho_c = \frac{3M}{4\pi R^3} </math> .
Hence the characteristic time and acceleration are, respectively,
<math>
\tau_\mathrm{SSC} = \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} =
\biggl[ \frac{2R^3 }{GM} \biggr]^{1/2} =
\biggl[ \frac{3}{2\pi G\rho_c} \biggr]^{1/2},
</math>
and,
<math>
g_\mathrm{SSC} = \frac{P_c}{R \rho_c} = \biggl( \frac{GM}{2R^2} \biggr) .
</math>
The required functions are,
- Density:
<math>\frac{\rho_0(r_0)}{\rho_c} = 1 </math> ;
- Pressure:
<math>\frac{P_0(r_0)}{P_c} = 1 - \chi_0^2 </math> ;
- Gravitational acceleration:
<math>
\frac{g_0(r_0)}{g_\mathrm{SSC}} = 2\chi_0 .
</math>
So our desired Eigenvalues and Eigenvectors will be solutions to the following ODE:
<math>
\frac{1}{(1 - \chi_0^2)} \biggl\{ (1 - \chi_0^2) \frac{d^2x}{d\chi_0^2} + \frac{4}{\chi_0}\biggl[1 - \frac{3}{2}\chi_0^2 \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl[\tau_\mathrm{SSC}^2 \omega^2 + 2 (4 - 3\gamma_\mathrm{g}) \biggr] x \biggr\} = 0 .
</math>
Setup as Presented by Sterne (1937)
In §2 of his paper, Sterne (1937) details the structural properties of an equilibrium, uniform-density sphere as follows. (Text taken verbatim from Sterne's paper are presented here in green.) Given that the undisturbed density is constant and equal to the mean density, <math>~\bar\rho</math>, the mass within any radius is,
<math>M_r = \biggl( \frac{4\pi}{3} \biggr) \bar\rho \xi_0^3 \, ;</math>
the undisturbed values of gravity and the pressure are, respectively,
<math>g_0 \equiv \frac{GM_r}{\xi_0^2} = \biggl( \frac{4\pi}{3} \biggr) G\bar\rho R x \, </math>
and
<math>P_0 = \biggl( \frac{2\pi}{3} \biggr) G R^2 \bar\rho^2(1 - x^2) \, ;</math>
and the quantity,
<math>\mu \equiv \frac{g_0 \bar\rho \xi_0}{P_0} = \frac{2x^2}{(1-x^2)} \, .</math>
Hence, for this particular equilibrium model, Sterne's derived wave equation — his equation (1.91), as displayed above — becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\xi_1^{ ' ' } + \biggl[\frac{4-\mu}{x} \biggr]\xi_1^' + \frac{R\bar\rho}{P_0} \biggl( \frac{n^2 R}{\gamma} - \frac{\alpha g_0}{x} \biggr) \xi_1</math> |
|
|
<math>~=</math> |
<math>~\xi_1^{ ' ' } + \frac{1}{x}\biggl[4 -\frac{2x^2}{(1-x^2)} \biggr]\xi_1^' + \frac{3}{2\pi G R \bar\rho (1 - x^2)}\biggl[ \frac{n^2 R}{\gamma} - \biggl( \frac{4\pi}{3} \biggr) \alpha G\bar\rho R \biggr] \xi_1</math> |
|
|
<math>~=</math> |
<math>~(1-x^2) \xi_1^{ ' ' } + \frac{1}{x}\biggl[4(1-x^2) - 2x^2 \biggr]\xi_1^' + \biggl[ \frac{3n^2 }{2\pi \gamma G \bar\rho} - 2 \alpha \biggr] \xi_1</math> |
|
|
<math>~=</math> |
<math>~(1-x^2) \xi_1^{ ' ' } + \frac{1}{x}\biggl[4 - 6x^2 \biggr]\xi_1^' + \mathfrak{F} \xi_1 \, ,</math> |
where,
<math>~\mathfrak{F} \equiv \frac{3n^2 }{2\pi \gamma G \bar\rho} - 2 \alpha \, .</math>
Note that, once the value of the parameter, <math>~\mathfrak{F}</math>, has been determined for a given eigenfunction, the square of the eigenfrequency will also be known via the inversion of this last expression. Specifically, in terms of <math>~\mathfrak{F}</math>,
|
<math>~n^2</math> |
<math>~=</math> |
<math>~\frac{2\pi \gamma G \bar\rho}{3} \biggl[ \mathfrak{F} + 2 \biggl(3-\frac{4}{\gamma}\biggr)\biggr]</math> |
|
<math>~\Rightarrow ~~~~~ \frac{n^2}{4\pi G \bar\rho}</math> |
<math>~=</math> |
<math>~\biggl(1 + \frac{\mathfrak{F}}{6} \biggr)\gamma -\frac{4}{3} \, .</math> |
Sterne's General Solution
In what follows, text presented in a green font has been taken verbatim from the paper by Sterne (1937). Sterne begins by writing the unknown eigenvector as a power series expanded about the origin, specifically,
|
<math>~\xi_1</math> |
<math>~=</math> |
<math>~\sum\limits_{0}^{\infty} a_k x^k \, ,</math> |
with, <math>~a_0 = 1</math>. It is found by substitution that the terms in odd powers of <math>~x</math> vanish, and that the coefficients of the even terms satisfy the recurrence formula,
|
<math>~a_{k+2}</math> |
<math>~=</math> |
<math>~a_k \cdot \frac{k^2 + 5k - \mathfrak{F}}{(k+2)(k+5)} \, .</math> |
The wave equation and attending boundary conditions will all be satisfied if we choose <math>\mathfrak{J}</math> so as to make the series solution terminate with some term, say the <math>~2 j^\mathrm{th}</math> where <math>~j</math> is zero or any positive integer. This it will do [via the above recurrence relation] if,
<math>~\mathfrak{F} = 2j(2j+5) \, .</math>
The first few solutions are displayed in the following boxed-in image that has been extracted directly from §2 (p. 587) of Sterne (1937); to the right of Sterne's table, we have added a column that expressly records the value of the square of the normalized eigenfrequency that corresponds to each of Sterne's solutions.
|
Table extracted from T. E. Sterne (1937)
"Modes of Radial Oscillation"
Monthly Notices of the Royal Astronomical Society, vol. 97, pp. 582 - © Royal Astronomical Society |
<math>~\frac{n^2}{4\pi G \bar\rho}</math> |
|---|---|
| <math>~\gamma - 4/3</math> | |
| <math>~2(5\gamma - 2)/3</math> | |
| <math>~7\gamma - 4/3</math> | |
| <math>~12\gamma - 4/3</math> |
Stability
The Adiabatic Wave Equation that defines this eigenvalue problem has been derived from the fundamental set of nonlinear Principal Governing Equations by assuming that, for example, the radial position, <math>~r(m,t)</math>, at any time, <math>~t</math>, and of each mass shell throughout our spherical configuration can be described by the expression,
<math>~r(m,t) = r_0(m) [ 1 + x(m) e^{i\omega t} ] \, ,</math>
where, the fractional displacement, <math>~|x| \ll 1</math>. Switching to Sterne's variable notation, this should be written as,
<math>~\xi(x,t) = \xi_0(x) [ 1 + A\xi_1(x) e^{i n t} ] \, ,</math>
with the presumption that the coefficient, <math>~|A| \ll 1</math>, and the understanding that, in Sterne's presentation, the variable, <math>~x</math>, is used to identify individual mass shells. Specifically, given <math>~R</math> and <math>~\bar\rho</math>,
<math>~m \equiv M_r = \frac{4}{3}\pi \xi_0^3 \bar\rho = \frac{4}{3}\pi (R x)^3 \bar\rho </math> <math>~\Rightarrow</math> <math>~x = \biggl( \frac{3m}{4\pi R^3 \bar\rho} \biggr)^{1/3} \, .</math>
Sterne's general solution of this eigenvalue problem describes mathematically how a self-gravitating, uniform-density configuration will vibrate if perturbed away from its equilibrium state; the oscillatory behavior associated with each pure radial mode, <math>~j</math> — among an infinite number of possible modes — is fully defined by the polynomial expression for the eigenvector, <math>~\xi_1(x)</math>, and the corresponding value of the square of the eigenfrequency, <math>~n^2</math>.
If, for any mode, <math>~j</math>, the square of the derived eigenfrequency, <math>~n^2</math>, is positive, then the eigenfrequency itself will be a real number — specifically,
<math>~n = \pm \sqrt{|n^2|} \, .</math>
As a result, the radial location of every mass shell will vary sinusoidally in time according to the expression,
<math>~\frac{\xi(x,t)}{\xi_0} - 1 \propto e^{\pm i \sqrt{|n^2|} t} \, .</math>
If, on the other hand, <math>~n^2</math>, is negative, then the eigenfrequency will be an imaginary number — specifically,
<math>~n = \pm i \sqrt{|n^2|} \, .</math>
As a result, the radial location of every mass shell will grow (or damp) exponentially in time according to the expression,
<math>~\frac{\xi(x,t)}{\xi_0} - 1 \propto e^{\pm \sqrt{|n^2|} t} \, .</math>
This latter condition is the mark of a dynamically unstable system. It is in this manner that the solution to an eigenvalue problem can provide critical information regarding the relative stability of equilibrium configurations.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |