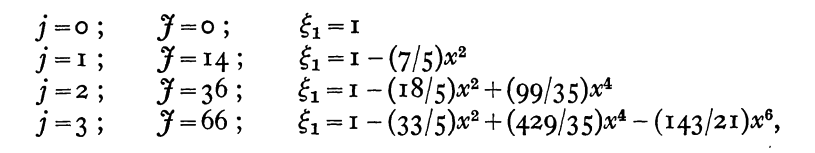Difference between revisions of "User:Tohline/SSC/UniformDensity"
(→Sterne's General Solution: Enter Sterne's series solution) |
(→Sterne's General Solution: Insert table of solutions from Sterne) |
||
| Line 381: | Line 381: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~a_k \cdot \frac{k^2 + 5k - \mathfrak{ | <math>~a_k \cdot \frac{k^2 + 5k - \mathfrak{F}}{(k+2)(k+5)} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 389: | Line 389: | ||
The wave equation and attending boundary conditions will all <font color="green">be satisfied if we choose <math>\mathfrak{J}</math> so as to make the series solution terminate with some term, say the <math>~2 j^\mathrm{th}</math> where <math>~j</math> is zero or any positive integer. This it will do</font> [via the above recurrence relation] if, | The wave equation and attending boundary conditions will all <font color="green">be satisfied if we choose <math>\mathfrak{J}</math> so as to make the series solution terminate with some term, say the <math>~2 j^\mathrm{th}</math> where <math>~j</math> is zero or any positive integer. This it will do</font> [via the above recurrence relation] if, | ||
<div align="center"> | <div align="center"> | ||
<math>~\mathfrak{ | <math>~\mathfrak{F} = 2j(2j+5) \, .</math> | ||
</div> | |||
The first few solutions are displayed in the following boxed-in image that has been extracted directly from §2 (p. 587) of [http://adsabs.harvard.edu/abs/1937MNRAS..97..582S Sterne (1937)]. | |||
<div align="center"> | |||
<table border="2" cellpadding="5"> | |||
<tr> | |||
<th align="center" colspan="1"> | |||
Table extracted from [http://adsabs.harvard.edu/abs/1937MNRAS..97..582S T. E. Sterne (1937)]<p></p> | |||
"''Modes of Radial Oscillation''"<p></p> | |||
Monthly Notices of the Royal Astronomical Society, vol. 97, pp. 582 - © [https://www.ras.org.uk/ Royal Astronomical Society] | |||
</th> | |||
<tr> | |||
<td colspan="1"> | |||
[[File:Sterne1937SolutionTable1.png|600px|center|Sterne (1937)]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
Revision as of 19:39, 15 June 2015
The Stability of Uniform-Density Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
As far as we have been able to determine, T. E. Sterne (1937, MNRAS, 97, 582) was the first to use linearized perturbation techniques and, specifically, the Adiabatic Wave Equation, to thoroughly analyze the stability of uniform-density, self-gravitating spheres. While uniform-density configurations present an overly simplified description of real stars, Sterne's (1937) stability analysis is an important one because it presents a complete spectrum of radial pulsation eigenfunctions — eigenfrequencies plus the corresponding eigenvectors — as closed-form analytic expressions. Such analytic solutions are quite rare in the context of studies of the structure, stability, and dynamics of self-gravitating fluids.
As has been explained in an accompanying introductory discussion, this type of stability analysis requires the solution of an eigenvalue problem. Here we begin by re-presenting the governing 2nd-order ODE (the Adiabatic Wave Equation) as it was derived in the accompanying introductory discussion, along with the specification of two customarily used boundary conditions; and we review the properties of the equilibrium configuration — also derived in a separate discussion — that are relevant to this stability analysis. Interleaved with this presentation, we also show the governing wave equation as it was derived by Sterne (1937) — and a table that translates from Sterne's notation to ours — along with his corresponding review of the properties of the unperturbed equilibrium configuration. Finally, we present Sterne's (1937) solution to this eigenvalue problem and discuss the properties of his derived radial pulsation eigenfunctions.
The Eigenvalue Problem
Our Approach
As has been derived in an accompanying discussion, the second-order ODE that defines the relevant Eigenvalue problem is,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 .
</math>
where the dimensionless radius,
<math>
\chi_0 \equiv \frac{r_0}{R} ,
</math>
the characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) is,
<math>
\tau_\mathrm{SSC} \equiv \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} ,
</math>
and the characteristic gravitational acceleration is,
<math>
g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} .
</math>
The two boundary conditions are,
<math>~\frac{dx}{d\chi_0} = 0</math> at <math>~\chi_0 = 0 \, ;</math>
and,
|
<math>~ \frac{d\ln x}{d\chi_0}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) </math> at <math>~\chi_0 = 1 \, .</math> |
The Approach Taken by Sterne (1937)
T. E. Sterne (1937) begins his analysis by deriving the
Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
in a manner explicitly designed to reproduce Eddington's pulsation equation — it appears as equation (1.8) in Sterne's paper — and, along with it, the surface boundary condition,
|
<math>~ r_0 \frac{d\ln x}{dr_0}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) </math> at <math>~r_0 = R \, ,</math> |
which appears in Sterne's paper as equation (1.9). Then, as shown in the following paragraph extracted directly from his paper, Sterne (1937) rewrites both of these expressions in, what he considers to be, "more convenient forms."
|
Paragraph extracted from T. E. Sterne (1937)
"Modes of Radial Oscillation"
Monthly Notices of the Royal Astronomical Society, vol. 97, pp. 582 - © Royal Astronomical Society |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||
Properties of the Equilibrium Configuration
Our Setup
From our derived structure of a uniform-density sphere, in terms of the configuration's radius <math>R</math> and mass <math>M</math>, the central pressure and density are, respectively,
<math>P_c = \frac{3G}{8\pi}\biggl( \frac{M^2}{R^4} \biggr) </math> ,
and
<math>\rho_c = \frac{3M}{4\pi R^3} </math> .
Hence the characteristic time and acceleration are, respectively,
<math>
\tau_\mathrm{SSC} = \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} =
\biggl[ \frac{2R^3 }{GM} \biggr]^{1/2} =
\biggl[ \frac{3}{2\pi G\rho_c} \biggr]^{1/2},
</math>
and,
<math>
g_\mathrm{SSC} = \frac{P_c}{R \rho_c} = \biggl( \frac{GM}{2R^2} \biggr) .
</math>
The required functions are,
- Density:
<math>\frac{\rho_0(r_0)}{\rho_c} = 1 </math> ;
- Pressure:
<math>\frac{P_0(r_0)}{P_c} = 1 - \chi_0^2 </math> ;
- Gravitational acceleration:
<math>
\frac{g_0(r_0)}{g_\mathrm{SSC}} = 2\chi_0 .
</math>
So our desired Eigenvalues and Eigenvectors will be solutions to the following ODE:
<math>
\frac{1}{(1 - \chi_0^2)} \biggl\{ (1 - \chi_0^2) \frac{d^2x}{d\chi_0^2} + \frac{4}{\chi_0}\biggl[1 - \frac{3}{2}\chi_0^2 \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl[\tau_\mathrm{SSC}^2 \omega^2 + 2 (4 - 3\gamma_\mathrm{g}) \biggr] x \biggr\} = 0 .
</math>
Setup as Presented by Sterne (1937)
In §2 of his paper, Sterne (1937) details the structural properties of an equilibrium, uniform-density sphere as follows. (Text taken verbatim from Sterne's paper are presented here in green.) Given that the undisturbed density is constant and equal to the mean density, <math>~\bar\rho</math>, the mass within any radius is,
<math>M_r = \biggl( \frac{4\pi}{3} \biggr) \bar\rho \xi_0^3 \, ;</math>
the undisturbed values of gravity and the pressure are, respectively,
<math>g_0 \equiv \frac{GM_r}{\xi_0^2} = \biggl( \frac{4\pi}{3} \biggr) G\bar\rho R x \, </math>
and
<math>P_0 = \biggl( \frac{2\pi}{3} \biggr) G R^2 \bar\rho^2(1 - x^2) \, ;</math>
and the quantity,
<math>\mu \equiv \frac{g_0 \bar\rho \xi_0}{P_0} = \frac{2x^2}{(1-x^2)} \, .</math>
Hence, for this particular equilibrium model, Sterne's derived wave equation — his equation (1.91), as displayed above — becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\xi_1^{ ' ' } + \biggl[\frac{4-\mu}{x} \biggr]\xi_1^' + \frac{R\bar\rho}{P_0} \biggl( \frac{n^2 R}{\gamma} - \frac{\alpha g_0}{x} \biggr) \xi_1</math> |
|
|
<math>~=</math> |
<math>~\xi_1^{ ' ' } + \frac{1}{x}\biggl[4 -\frac{2x^2}{(1-x^2)} \biggr]\xi_1^' + \frac{3}{2\pi G R \bar\rho (1 - x^2)}\biggl[ \frac{n^2 R}{\gamma} - \biggl( \frac{4\pi}{3} \biggr) \alpha G\bar\rho R \biggr] \xi_1</math> |
|
|
<math>~=</math> |
<math>~(1-x^2) \xi_1^{ ' ' } + \frac{1}{x}\biggl[4(1-x^2) - 2x^2 \biggr]\xi_1^' + \biggl[ \frac{3n^2 }{2\pi \gamma G \bar\rho} - 2 \alpha \biggr] \xi_1</math> |
|
|
<math>~=</math> |
<math>~(1-x^2) \xi_1^{ ' ' } + \frac{1}{x}\biggl[4 - 6x^2 \biggr]\xi_1^' + \mathfrak{J} \xi_1 \, ,</math> |
where,
<math>~\mathfrak{J} \equiv \frac{3n^2 }{2\pi \gamma G \bar\rho} - 2 \alpha \, .</math>
Analytic Solution
First few lowest-order modes
- Mode 0:
- <math>x_0 = \mathrm{constant}</math>, in which case,
<math> \omega_0^2 = - 2(4 - 3\gamma_\mathrm{g})\biggl[ \frac{2\pi G\rho_c}{3} \biggr] = 4\pi G \rho_c \biggl[ \gamma_\mathrm{g}- \frac{4}{3} \biggr] </math>
- Mode 1:
- <math>x_1 = a + b\chi_0^2</math>, in which case,
<math> \frac{dx}{d\chi_0} = 2b\chi_0; ~~~~ \frac{d^2 x}{d\chi_0^2} = 2b; </math>
<math>
\frac{1}{(1 - \chi_0^2)} \biggl\{ 2b (1 - \chi_0^2) + 8b \biggl[1 - \frac{3}{2}\chi_0^2 \biggr] + A_1 \biggl(1 + \frac{b}{a}\chi_0^2 \biggr) \biggr\} = 0 ,
</math>
where,
<math> A_1 \equiv \frac{a}{\gamma_\mathrm{g}}\biggl[ \biggl( \frac{3}{2\pi G\rho_c} \biggr) \omega_1^2+ 2(4 - 3\gamma_\mathrm{g}) \biggr] . </math>
Therefore,
<math>
(A_1 + 10b) + \biggl[ \biggl(\frac{b}{a}\biggr) A_1 - 14b \biggr] \chi_0^2 = 0 ,
</math>
<math>
\Rightarrow ~~~~~ A_1 = - 10b ~~~~~\mathrm{and} ~~~~~ A_1 = 14a
</math>
<math>
\Rightarrow ~~~~~ \frac{b}{a} = -\frac{7}{5} ~~~~~\mathrm{and} ~~~~~ \frac{A_1}{a} = 14 = \frac{1}{\gamma_\mathrm{g}}\biggl[ \biggl( \frac{3}{2\pi G\rho_c} \biggr) \omega_1^2+ 2(4 - 3\gamma_\mathrm{g}) \biggr] .
</math>
Hence,
<math>
\biggl( \frac{3}{2\pi G\rho_c} \biggr) \omega_1^2 = 20\gamma_\mathrm{g} -8
</math>
<math>
\Rightarrow ~~~~~ \omega_1^2 = \frac{2}{3}\biggl( 4\pi G\rho_c \biggr) (5\gamma_\mathrm{g} -2)
</math>
and, to within an arbitrary normalization factor,
<math> x_1 = 1 - \frac{7}{5}\chi_0^2 . </math>
Sterne's General Solution
In what follows, text presented in a green font has been taken verbatim from the paper by Sterne (1937). Sterne begins by writing the unknown eigenvector as a power series expanded about the origin, specifically,
|
<math>~\xi_1</math> |
<math>~=</math> |
<math>~\sum\limits_{0}^{\infty} a_k x^k \, ,</math> |
with, <math>~a_0 = 1</math>. It is found by substitution that the terms in odd powers of <math>~x</math> vanish, and that the coefficients of the even terms satisfy the recurrence formula,
|
<math>~a_{k+2}</math> |
<math>~=</math> |
<math>~a_k \cdot \frac{k^2 + 5k - \mathfrak{F}}{(k+2)(k+5)} \, .</math> |
The wave equation and attending boundary conditions will all be satisfied if we choose <math>\mathfrak{J}</math> so as to make the series solution terminate with some term, say the <math>~2 j^\mathrm{th}</math> where <math>~j</math> is zero or any positive integer. This it will do [via the above recurrence relation] if,
<math>~\mathfrak{F} = 2j(2j+5) \, .</math>
The first few solutions are displayed in the following boxed-in image that has been extracted directly from §2 (p. 587) of Sterne (1937).
|
Table extracted from T. E. Sterne (1937)
"Modes of Radial Oscillation"
Monthly Notices of the Royal Astronomical Society, vol. 97, pp. 582 - © Royal Astronomical Society |
|---|
n=1 Polytrope
This discussion has been moved to another chapter.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |