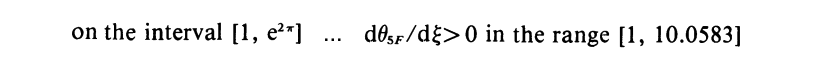Difference between revisions of "User:Tohline/SSC/Structure/Polytropes"
(→Function Properties: Draw connection between the astrophysically relevant function properties and the example discussion that follows) |
(→Srivastava's F-Type Solution: Add details of solution to cubic equation as well as image from WolframAlpha's widget) |
||
| Line 865: | Line 865: | ||
</table> | </table> | ||
</div> | </div> | ||
<div align="center"> | |||
<table border="1" cellpadding="8" width="80%"> | |||
<tr> | |||
<td align="left"> | |||
<font color="red">'''ASIDE:'''</font> As is well known and documented — see, for example [http://mathworld.wolfram.com/CubicFormula.html Wolfram MathWorld] or [http://en.wikipedia.org/wiki/Cubic_function Wikipedia's discussion] of the topic — the roots of any cubic equation can be determined analytically. In order to evaluate the root(s) of our particular cubic equation, we have drawn from the utilitarian [http://www.math.vanderbilt.edu/~schectex/courses/cubic/ online summary provided by Eric Schechter at Vanderbilt University]. For a cubic equation of the general form, | |||
<div align="center"> | |||
<math>~ay^3 + by^2 + cy + d = 0 \, ,</math> | |||
</div> | |||
a real root is given by the expression, | |||
<div align="center"> | |||
<math>~ | |||
y = p + \{q + [q^2 + (r-p^2)^3]^{1/2}\}^{1/3} + \{q - [q^2 + (r-p^2)^3]^{1/2}\}^{1/3} | |||
\, ,</math> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<math>~p \equiv -\frac{b}{3a} \, ,</math> | |||
<math>~q \equiv \biggl[p^3 + \frac{bc-3ad}{6a^2} \biggr] \, ,</math> | |||
and | |||
<math>~r=\frac{c}{3a} \, .</math> | |||
</div> | |||
In our particular case, | |||
<div align="center"> | |||
<math>~a =1\, ,</math> | |||
<math>~b =-3\, ,</math> | |||
<math>~c = +3 \, ,</math> | |||
and | |||
<math>~d = - 3 \, .</math> | |||
</div> | |||
Hence, interestingly enough, | |||
<div align="center"> | |||
<math>~p = q = r = + 1 \, ,</math> | |||
</div> | |||
which implies that the real root is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~y</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 + \{2\}^{1/3} + \{0\}^{1/3} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
(There is also a pair of imaginary roots, but they are irrelevant in the context of our overarching astrophysical discussion.) | |||
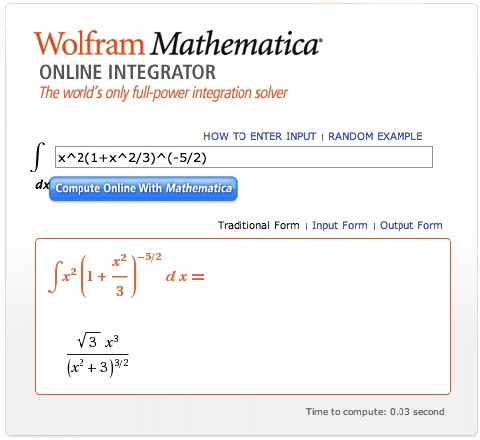
Just for fun, we also used WolframAlpha's online "cubic equation solver" widget to find the root(s) of our specific cubic equation. The image shown here, on the right, displays the key result that was returned by this WolframAlpha widget. | |||
</td> | |||
<td align="center"> | |||
[[File:WolframAlphaCubicSolver.png|200px|center|WolframAlpha's "Cubic Equation Solver" widget]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The single, real root of this cubic equation is, | The single, real root of this cubic equation is, | ||
<div align="center"> | <div align="center"> | ||
Revision as of 23:25, 17 April 2015
Polytropic Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Here we will supplement the simplified set of principal governing equations with a polytropic equation of state, as defined in our overview of Problems supplemental relations for time-independent problems. Specifically, we will assume that <math>~\rho</math> is related to <math>~H</math> through the relation,
<math>~\rho = \biggl[ \frac{H}{(n+1)K_\mathrm{n}} \biggr]^n </math>
It will be useful to note as well that, for any polytropic gas, the three key state variables are always related to one another through the simple expression,
<math> ~(n+1) P = H\rho</math> .
Governing Relations
Lane-Emden Equation
Adopting solution technique #2, we need to solve the following second-order ODE relating the two unknown functions, <math>~\rho</math> and <math>~H</math>:
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{dH}{dr} \biggr) =- 4\pi G \rho</math> .
It is customary to replace <math>~H</math> and <math>~\rho</math> in this equation by a dimensionless polytropic enthalpy, <math>\Theta_H</math>, such that,
<math> \Theta_H \equiv \frac{H}{H_c} = \biggl( \frac{\rho}{\rho_c} \biggr)^{1/n} , </math>
where the mathematical relationship between <math>~H</math>/<math>H_c</math> and <math>~\rho</math>/<math>\rho_c</math> comes from the adopted barotropic (polytropic) relation identified above. To accomplish this, we replace <math>~H</math> with <math>H_c \Theta_H</math> on the left-hand-side of the governing differential equation and we replace <math>~\rho</math> with <math>\rho_c \Theta_H^n</math> on the right-hand-side, then gather the constant coefficients together on the left. The resulting ODE is,
<math>\biggl[ \frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr) \biggr] \frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{d\Theta_H}{dr} \biggr) = - \Theta_H^n</math> .
The term inside the square brackets on the left-hand-side has dimensions of length-squared, so it is also customary to define a dimensionless radius,
<math> \xi \equiv \frac{r}{a_\mathrm{n}} , </math>
where,
<math>~ a_\mathrm{n} \equiv \biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)\biggr]^{1/2} = \biggl[\frac{(n+1)K_n}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \, , </math>
in which case our governing ODE becomes what is referred to in the astronomical literature as the,
Lane-Emden Equation
|
<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math> |
Our task is to solve this ODE to determine the behavior of the function <math>~\Theta_H(\xi)</math> — and, from it in turn, determine the radial distribution of various dimensional physical variables — for various values of the polytropic index, <math>~n</math>.
Boundary Conditions
Given that it is a <math>2^\mathrm{nd}</math>-order ODE, a solution of the Lane-Emden equation will require specification of two boundary conditions. Based on our definition of the variable <math>\Theta_H</math>, one obvious boundary condition is to demand that <math>~\Theta_H = 1</math> at the center (<math>~\xi=0</math>) of the configuration. In astrophysically interesting structures, we also expect the first derivative of many physical variables to go smoothly to zero at the center of the configuration — see, for example, the radial behavior that was derived for <math>~P</math>, <math>~H</math>, and <math>~\Phi</math> in a uniform-density sphere. Hence, we will seek solutions to the Lane-Emden equation where <math>~d\Theta_H /d\xi = 0</math> at <math>~\xi=0</math> as well.
Known Analytic Solutions
While the Lane-Emden equation has been studied for over 100 years, to date, analytic solutions to the equation (subject to the above specified boundary conditions) have been found only for three values of the polytropic index, <math>~n</math>. We will review these three solutions here.
<math>~n</math> = 0 Polytrope
When the polytropic index, <math>~n</math>, is set equal to zero, the right-hand-side of the Lane-Emden equation becomes a constant (<math>-1</math>), so the equation can be straightforwardly integrated, twice, to obtain the desired solution for <math>\Theta_H(\xi)</math>. Specifically, the first integration along with enforcement of the boundary condition on <math>d\Theta_H/d\xi</math> at the center gives,
<math> \xi^2 \frac{d\Theta_H}{d\xi} = - \frac{1}{3}\xi^3 . </math>
Then the second integration along with enforcement of the boundary condition on <math>\Theta_H</math> at the center gives,
<math> \Theta_H = 1 - \frac{1}{6}\xi^2 . </math>
This function varies smoothly from unity at <math>\xi = 0</math> (as required by one of the boundary conditions) to zero at <math>\xi = \xi_1 = \sqrt{6}</math> (by tradition, the subscript "1" is used to indicate that it is the "first" zero of the Lane-Emden function), then becomes negative for values of <math>\xi > \xi_1</math>.
The astrophysically interesting surface of this spherical configuration is identified with the first zero of the function, that is, where the dimensionless enthalpy first goes to zero. In other words, the dimensionless radius <math>\xi_1</math> should correspond with the dimensional radius of the configuration, <math>R</math>. From the definition of <math>\xi</math>, we therefore conclude that,
<math> a_{n=0} = \frac{R}{\xi_1} = \frac{R}{\sqrt{6}} , </math>
and
<math> \xi = \sqrt{6} \biggl(\frac{r}{R} \biggr) , </math>
Hence, the Lane-Emden function solution can also be written as,
<math> \Theta_H = \frac{H}{H_c} = 1 - \biggl(\frac{r}{R}\biggr)^2 . </math>
Since,
<math> a_{n=0}^2 = \frac{1}{4\pi G} \biggl(\frac{H_c}{\rho_c}\biggr) = \frac{R^2}{6} , </math>
we also conclude that,
<math> H_c = \frac{2\pi G}{3} \rho_c R^2 . </math>
This, combined with the Lane-Emden function solution, tells us that the run of enthalpy through the configuration is,
<math> H(r) = \frac{2\pi G}{3} \rho_c R^2 \biggl[ 1 - \biggl(\frac{r}{R}\biggr)^2 \biggr]. </math>
Now, it is always true for polytropic structures — see, for example, expressions at the top of this page of discussion — that <math>~\rho</math> can be related to <math>~H</math> through the expression,
<math> \biggl( \frac{\rho}{\rho_c} \biggr) = \biggl( \frac{H}{H_c} \biggr)^n = \Theta_H^n . </math>
Hence, for the specific case of an <math>~n</math> = 0 polytrope, we deduce that
<math> \frac{\rho}{\rho_c} = 1 . </math>
This means that an <math>~n</math> = 0 polytropic sphere is also a uniform-density sphere. It should come as no surprise to discover, therefore, that the functional behavior of <math>~H</math><math>(r)</math> we have derived for the <math>~n</math> = 0 polytrope is identical to the <math>~H</math><math>(r)</math> function that we have derived elsewhere for uniform-density spheres. All of the other summarized properties of uniform-density spheres can therefore also be assigned as properties of <math>~n</math> = 0 polytropes.
<math>~n</math> = 1 Polytrope
Primary E-Type Solution
When the polytropic index, <math>~n</math>, is set equal to unity, the Lane-Emden equation takes the form of an inhomogeneous, <math>2^\mathrm{nd}</math>-order ODE that is linear in the unknown function, <math>\Theta_H</math>. Specifically, to derive the radial distribution of the Lane-Emden function <math>\Theta_H(r)</math> for an <math>~n</math> = 1 polytrope, we must solve,
<math>\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H</math> ,
subject to the above-specified boundary conditions. If we multiply this equation through by <math>\xi^2</math> and move all the terms to the left-hand-side, we see that the governing ODE takes the form,
<math>\xi^2 \frac{d^2\Theta_H}{d\xi^2} + 2\xi \frac{d\Theta_H}{d\xi} + \xi^2 \Theta_H</math> = 0 ,
which is a relatively familiar <math>2^\mathrm{nd}</math>-order ODE (the spherical Bessel differential equation) whose general solution involves a linear combination of the order zero spherical Bessel functions of the first and second kind, respectively,
<math> j_0(\xi) = \frac{\sin\xi}{\xi} , </math>
and,
<math> y_0(\xi) = - \frac{\cos\xi}{\xi} . </math>
Given the boundary conditions that have been imposed on our astrophysical problem, we can rule out any contribution from the <math>y_0</math> function. The desired solution is,
<math> \Theta_H(\xi) = j_0(\xi) = \frac{\sin\xi}{\xi} . </math>
This function is also referred to as the (unnormalized) sinc function.
Because, by definition, <math>H/H_c = \Theta_H</math>, and for an <math>~n</math> = 1 polytrope <math>\rho/\rho_c = H/H_c</math>, we can immediately conclude from this Lane-Emden function solution that,
<math> \frac{\rho(\xi)}{\rho_c} = \frac{H(\xi)}{H_c} = \frac{\sin\xi}{\xi} . </math>
Furthermore, because the relation (<math>~n</math> + 1)<math>~P</math> = <math>~H</math><math>~\rho</math> holds for all polytropic gases, we conclude that the pressure distribution inside an <math>~n</math> = 1 polytrope is,
<math> \frac{P(\xi)}{P_c} = \biggl( \frac{\sin\xi}{\xi} \biggr)^2 . </math>
The functions <math>~P</math><math>(\xi)</math>, <math>~H</math><math>(\xi)</math>, and <math>~\rho</math><math>(\xi)</math> all first drop to zero when <math>\xi = \pi</math>. Hence, for an <math>~n</math> = 1 polytrope, <math>\xi_1 = \pi</math> and, in terms of the configuration's radius <math>R</math>, the polytropic scale length is,
<math> a_{n=1} = \frac{R}{\xi_1} = \frac{R}{\pi} . </math>
So, throughout the configuration, we can relate <math>\xi</math> to the dimensional spherical coordinate <math>r</math> through the relation,
<math> \xi = \pi \biggl(\frac{r}{R}\biggr) ; </math>
and, from the general definition of <math>a_n</math>, the central value of <math>~H</math> can be expressed in terms of <math>R</math> and <math>\rho_c</math> via the relation,
<math> H_c = \frac{4G}{\pi}\rho_c R^2 . </math>
Again because the relation (<math>~n</math> + 1)<math>~P</math> = <math>~H</math><math>~\rho</math> must hold everywhere inside a polytrope, this means that the central pressure is given by the expression,
<math> P_c = \frac{2G}{\pi}\rho_c^2 R^2 . </math>
Given the radial distribution of <math>~\rho</math>, we can determine the functional behavior of the integrated mass. Specifically,
|
<math> M_r(\xi) </math> |
<math>=</math> |
<math> \int_0^r 4\pi r^2 \rho~ dr </math> | |
|
|
<math>=</math> |
<math> 4\pi \rho_c \biggl(\frac{R}{\pi}\biggr)^3 \int_0^\xi \xi\sin\xi ~d\xi </math> |
|
|
|
<math>=</math> |
<math> \frac{4}{\pi^2} \rho_c R^3 [ \sin\xi - \xi\cos\xi ] \, . </math> |
Because <math>\xi = \pi</math> at the surface of this spherical configuration — in which case the term inside the square brackets is <math>\pi</math> — we conclude as well that the total mass of the configuration is,
<math> M = \frac{4}{\pi}\rho_c R^3 . </math>
Summary
From the above derivations, we can describe the properties of a spherical <math>~n</math> = 1 polytrope as follows:
- Mass:
- Given the density, <math>\rho_c</math>, and the radius, <math>R</math>, of the configuration, the total mass is,
<math>M = \frac{4}{\pi} \rho_c R^3 </math> ;
- and, expressed as a function of <math>M</math>, the mass that lies interior to radius <math>r</math> is,
<math>\frac{M_r}{M} = \frac{1}{\pi} \biggl[ \sin\biggl(\frac{\pi r}{R} \biggr) - \biggl(\frac{\pi r}{R} \biggr)\cos\biggl(\frac{\pi r}{R} \biggr) \biggr]</math> .
- Pressure:
- Given values for the pair of model parameters <math>( \rho_c , R )</math>, or <math>( M , R )</math>, or <math>( \rho_c , M )</math>, the central pressure of the configuration is,
<math>P_c = \frac{2 G}{\pi} \rho_c^2 R^2 = \frac{\pi G}{8}\biggl( \frac{M^2}{R^4} \biggr) = \biggl[ \frac{1}{2\pi} G^3 \rho_c^4 M^2 \biggr]^{1/3}</math> ;
- and, expressed in terms of the central pressure <math>P_c</math>, the variation with radius of the pressure is,
<math>P(r)= P_c \biggl[\frac{R}{\pi r} \sin\biggl(\frac{\pi r}{R}\biggr) \biggr]^2</math> .
- Enthalpy:
- Throughout the configuration, the enthalpy is given by the relation,
<math>H(r) = \frac{2 P(r)}{ \rho(r)} = \frac{GM}{R} \biggl[\frac{R}{\pi r} \sin\biggl(\frac{\pi r}{R}\biggr) \biggr]</math> .
- Gravitational potential:
- Throughout the configuration — that is, for all <math>r \leq R</math> — the gravitational potential is given by the relation,
<math>\Phi_\mathrm{surf} - \Phi(r) = H(r) = \frac{GM}{R} \biggl[\frac{R}{\pi r} \sin\biggl(\frac{\pi r}{R}\biggr) \biggr] </math> .
- Outside of this spherical configuration— that is, for all <math>r \geq R</math> — the potential should behave like a point mass potential, that is,
<math>\Phi(r) = - \frac{GM}{r} </math> .
- Matching these two expressions at the surface of the configuration, that is, setting <math>\Phi_\mathrm{surf} = - GM/R</math>, we have what is generally considered the properly normalized prescription for the gravitational potential inside a spherically symmetric, <math>~n</math> = 1 polytropic configuration:
<math>\Phi(r) = - \frac{G M}{R} \biggl\{ 1 + \biggl[\frac{R}{\pi r} \sin\biggl(\frac{\pi r}{R}\biggr) \biggr] \biggr\} </math> .
- Mass-Radius relationship:
- We see that, for a given value of <math>\rho_c</math>, the relationship between the configuration's total mass and radius is,
<math>M \propto R^3 ~~~~~\mathrm{or}~~~~~R \propto M^{1/3} </math> .
- Central- to Mean-Density Ratio:
- The ratio of the configuration's central density to its mean density is,
<math>\frac{\rho_c}{\bar{\rho}} = \biggl(\frac{\pi M}{4 R^3} \biggr)\biggl(\frac{3 M}{4 \pi R^3} \biggr) = \frac{\pi^2}{3} </math> .
<math>~n</math> = 5 Polytrope
Primary E-Type Solution
To derive the radial distribution of the Lane-Emden function <math>\Theta_H(r)</math> for an <math>~n</math> = 5 polytrope, we must solve,
<math>\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - (\Theta_H)^5</math> ,
subject to the above-specified boundary conditions. Following Emden (1907), C67 (pp. 93-94) shows that by making the substitutions,
<math> \xi = \frac{1}{x} = e^{-t} \, ; ~~~~~\Theta_H = \biggl(\frac{x}{2}\biggr)^{1/2} z = \biggl(\frac{1}{2}e^t\biggr)^{1/2}z \, , </math>
the differential equation can be rewritten as,
<math> \frac{d^2 z}{dt^2} = \frac{1}{4}z (1 - z^4) \, . </math>
This equation has the solution,
<math> z = \pm \biggl[ \frac{12 C e^{-2t}}{(1 + C e^{-2t})^2} \biggr]^{1/4} \, , </math>
that is,
<math> \Theta_H = \biggl[ \frac{3 C }{(1 + C \xi^2)^2} \biggr]^{1/4} \, . </math>
where <math>C</math> is an integration constant. Because <math>\Theta_H</math> must go to unity when <math>\xi = 0</math>, we see that <math>C=1/3</math>. Hence,
<math> \Theta_H = \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-1/2} \, . </math>
From this Lane-Emden function solution, we obtain,
<math> \frac{\rho}{\rho_c} = \Theta_H^5 = \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-5/2} \, , </math>
and,
<math> \frac{P}{P_c} = \biggr(\frac{\rho}{\rho_c}\biggr)^{6/5} = \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3} \, . </math>
Notice that, for this polytropic structure, the density and pressure don't go to zero until <math>\xi \rightarrow \infty</math>. Hence, <math>\xi_1 = \infty</math>. However, the radial scale length,
<math> a_5 = \biggr[ \frac{1}{4\pi G} \biggl( \frac{H_c}{\rho_c} \biggr) \biggr]^{1/2} = \biggr[ \frac{(n+1)K}{4\pi G} \rho_c^{(1/n - 1)} \biggr]^{1/2} = \biggr[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_c^{-2/5} \, . </math>
Hence,
|
<math> M_r(\xi) </math> |
<math>=</math> |
<math> 4\pi \rho_c a_5^3 \int_0^\xi \xi^2 \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-5/2} d\xi </math> | |
|
|
<math>=</math> |
<math> 4\pi \biggr[ \frac{3K}{2\pi G} \biggr]^{3/2} \rho_c^{-1/5} ~\biggl\{ \frac{\sqrt{3} \xi^3}{(3 + \xi^2)^{3/2}} \biggr\} </math> |
|
|
|
<math>=</math> |
<math> \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_c^{-1/5} ~\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \} \, . </math> |
The function of <math>\xi</math> inside the curly brackets of this last expression goes to unity as <math>\xi \rightarrow \infty</math>, so the integrated mass is finite even though the configuration extends to infinity. Specifically, the total mass is,
<math>M = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_c^{-1/5} \, .</math>
We can invert this formula to obtain an expression for <math>K</math> in terms of <math>M</math> and <math>\rho_c</math>, namely,
<math> K = \biggr[ \frac{\pi M^2 G^3}{2\cdot 3^4} \biggr]^{1/3} \rho_c^{2/15} \, . </math>
This, in turn, means that the central pressure,
<math> P_c = K\rho_c^{6/5} = \biggr[ \frac{\pi M^2 G^3}{2\cdot 3^4} \biggr]^{1/3} \rho_c^{4/3} \, , </math>
and,
<math> H_c = \frac{6P_c}{\rho_c} = \biggr[ \frac{2^2 \pi M^2 G^3}{3} \biggr]^{1/3} \rho_c^{1/3} \, . </math>
Srivastava's F-Type Solution
Demonstration of Function's Validity
In a short paper, S. Srivastava (1968, ApJ, 136, 680) presents another, analytically prescribable solution to the Lane-Emden equation of index <math>~n = 5</math> that we will call upon in our discussion of one category of bipolytropic configurations. Rather than repeat Srivastava's derivation here, we will simply specify his functional solution then demonstrate that it satisfies the Lane-Emden equation. Srivastiva's Lane-Emden function is (see his equations 12 & 13),
|
<math>~\theta_{5F}</math> |
<math>~=</math> |
<math>~\frac{\sin[\ln(A\xi)^{1/2})]}{\xi^{1/2}\{3-2\sin^2[\ln(A\xi)^{1/2}]\}^{1/2}} \, ,</math> |
where, <math>~A</math> is an arbitrary (positive) constant. Adopting the shorthand notation,
<math>\Delta \equiv \ln(A\xi)^{1/2}\, ,</math>
and, recognizing that,
|
<math>\frac{d}{d\ln(A\xi)}\biggl[ \ln(A\xi)^{1/2} \biggr] = \frac{1}{2}</math> |
<math>~\Rightarrow~</math> |
<math>~\frac{d\Delta}{d\xi} = \frac{1}{2\xi} \, , </math> |
the first derivative of Srivastava's Lane-Emden function is,
|
<math>~\frac{d\theta_{5F}}{d\xi}</math> |
<math>~=</math> |
<math>~ \frac{\cos\Delta}{2\xi^{3/2}(3-2\sin^2\Delta)^{1/2}} - \frac{\sin\Delta}{2\xi^{3/2}(3-2\sin^2\Delta)^{1/2}} + \frac{\sin^2\Delta \cos\Delta }{\xi^{3/2}(3-2\sin^2\Delta)^{3/2}} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\xi^{3/2}(3-2\sin^2\Delta)^{3/2}} \biggl[ (\cos\Delta - \sin\Delta ) (3-2\sin^2\Delta) + 2\sin^2\Delta\cos\Delta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{3\cos\Delta-3\sin\Delta + 2\sin^3\Delta }{2\xi^{3/2}(3-2\sin^2\Delta)^{3/2}} \, . </math> |
Hence, the left-hand-side of the,
Lane-Emden Equation
|
<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math> |
is,
|
LHS |
<math>~=</math> |
<math>~ \frac{1}{\xi^2}\frac{d}{d\xi}\biggl[ \frac{\xi^{1/2}(3\cos\Delta-3\sin\Delta + 2\sin^3\Delta )}{2(3-2\sin^2\Delta)^{3/2}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\xi^2}\biggl[ \frac{(3\cos\Delta-3\sin\Delta + 2\sin^3\Delta )}{4\xi^{1/2}(3-2\sin^2\Delta)^{3/2}} + \frac{(-3\sin\Delta-3\cos\Delta + 6\sin^2\Delta \cos\Delta )}{4\xi^{1/2}(3-2\sin^2\Delta)^{3/2}} </math> |
|
|
|
<math>~ + \frac{3(3\cos\Delta-3\sin\Delta + 2\sin^3\Delta )\sin\Delta \cos\Delta}{2\xi^{1/2}(3-2\sin^2\Delta)^{5/2}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~2^{-2}\xi^{-5/2}(3-2\sin^2\Delta)^{-5/2} [ (3-2\sin^2\Delta) (3\cos\Delta-3\sin\Delta + 2\sin^3\Delta ) </math> |
|
|
|
<math>~+ (3-2\sin^2\Delta) (-3\sin\Delta-3\cos\Delta + 6\sin^2\Delta \cos\Delta ) + 6(3\cos\Delta-3\sin\Delta + 2\sin^3\Delta )\sin\Delta \cos\Delta ]</math> |
|
|
<math>~=</math> |
<math>~2^{-2}\xi^{-5/2}(3-2\sin^2\Delta)^{-5/2} [ (3-2\sin^2\Delta) (-6\sin\Delta + 2\sin^3\Delta + 6\sin^2\cos\Delta) </math> |
|
|
|
<math>~ + 6(3\cos\Delta-3\sin\Delta + 2\sin^3\Delta )\sin\Delta \cos\Delta ]</math> |
|
|
<math>~=</math> |
<math>~2^{-2}\xi^{-5/2}(3-2\sin^2\Delta)^{-5/2} [ -18\sin\Delta + 6\sin^3\Delta + 18\sin^2\cos\Delta + 12\sin^3\Delta - 4\sin^5\Delta -12\sin^4\cos\Delta </math> |
|
|
|
<math>~ + 18\sin\Delta \cos^2\Delta-18\sin^2\Delta \cos\Delta + 12\sin^4\Delta \cos\Delta ]</math> |
|
|
<math>~=</math> |
<math>~2^{-2}\xi^{-5/2}(3-2\sin^2\Delta)^{-5/2}[ -4\sin^5\Delta ] </math> |
|
|
<math>~=</math> |
<math>~- \theta_{5F}^5 \, . </math> |
This demonstrates that Srivastava's function satisfies the Lane-Emden equation of index <math>~n=5</math>.
Function Properties
The function, <math>~\theta_{5F}</math>, looks like a damped oscillator with the following specific properties:
- As <math>~\xi</math> increases from zero, the function oscillates with an ever increasing period; the function goes through zero when <math>~\Delta = \pm \pi m</math> (m is an integer), that is, when <math>~(A\xi) = e^{\pm 2\pi m}</math>.
- The amplitude of the oscillation drops approximately as <math>~\xi^{-1/2}</math>.
- In an astrophysical context, the function can be used as a physically realistic representation of a spherical shell inside of a self-gravitating configuration only over the interval of a single oscillation for which <math>~\theta_{5F}</math> is positive (ensuring that the mass density is everywhere positive) and, at the same time, <math>~d\theta_{5F}/d\xi</math> is negative (ensuring that the density and pressure are a decreasing function of the radial coordinate). In the following example, the astrophysically relevant segment of the function is identified with the parameter interval, <math>~\xi_\mathrm{crit} \le \xi \le e^{2\pi}</math>.
Example Interval
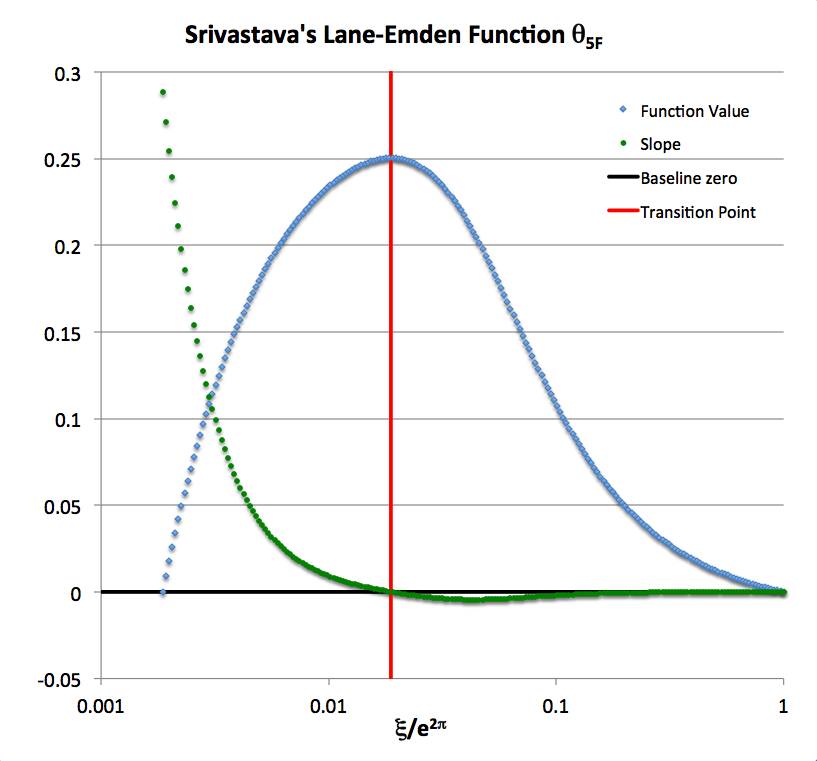
As an example, let's set <math>~A=1</math> and examine the oscillation interval between <math>~m=0</math> and <math>~m=1</math>, that is, over the range, <math>~0 \le \Delta \le \pi</math> which corresponds to the parameter interval <math>~\xi = [1, e^{2\pi}]</math>. The denominator of <math>~\theta_{5F}</math> is positive for all values of <math>~\xi</math> and, over this specified interval, the numerator of <math>~\theta_{5F}</math> is also always positive. The blue curve in the following figure presents a plot of <math>~\theta_{5F}(x)</math> and the green curve presents a plot of the first derivative (the slope) of the function <math>~d\theta_{5F}(x)/d\xi</math> over the desired interval, where <math>~x \equiv \xi/e^{2\pi}</math>; note that the horizontal axis is shown in logarithmic units.
|
Segment of <math>~\theta_{5F}</math> Function Derived by S. Srivastava (1968, ApJ, 136, 680) |
|---|
At both ends of the chosen parameter interval — that is, at <math>~\Delta = 0</math> and at <math>~\Delta = \pi</math> — the function <math>~\theta_{5F} = 0</math> and, correspondingly as depicted in the figure, the blue curve touches the horizontal axis. At the beginning of the interval (<math>~\Delta =0</math>), the slope of the function and, correspondingly, the green curve, has the (positive) value,
|
<math>~\frac{d\theta_{5F}}{d\xi}</math> |
<math>~=</math> |
<math>~ \frac{3\cos(0)-3\sin(0) + 2\sin^3(0) }{2\xi^{3/2}[3-2\sin^2(0)]^{3/2}} = \frac{3}{2(3^{3/2})} = (2^2 \cdot 3)^{-1/2} \approx 0.28868 \, . </math> |
At the end of the interval (<math>~\Delta=\pi</math>), the slope of the function as well as the green curve, has the (negative) value,
|
<math>~\frac{d\theta_{5F}}{d\xi}</math> |
<math>~=</math> |
<math>~ \frac{3\cos(\pi)-3\sin(\pi) + 2\sin^3(\pi) }{2\xi^{3/2}[3-2\sin^2(\pi)]^{3/2}} = \frac{-3}{2e^{3\pi}(3^{3/2})} = -e^{-3\pi} (2^2 \cdot 3)^{-1/2} \approx -2.3296 \times 10^{-5} \, . </math> |
Over this interval, <math>~\theta_{5F}</math> reaches its maximum when the slope of the function is zero, that is, at the value of <math>~\Delta</math> where,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~3\cos\Delta -3\sin\Delta +2(1-\cos^2\Delta)\sin\Delta</math> |
|
|
<math>~=</math> |
<math>~3\cos\Delta -\sin\Delta -2\cos^2\Delta \sin\Delta</math> |
|
<math>~\Rightarrow ~~~~1</math> |
<math>~=</math> |
<math>~3\cot\Delta -2\cos^2\Delta \, .</math> |
Rewriting both of these trigonometric functions in terms of the tangent function and adopting the shorthand notation,
<math>~y \equiv \tan\Delta \, ,</math>
this condition becomes,
|
<math>~1</math> |
<math>~=</math> |
<math>~\frac{3}{y} -\frac{2}{1+y^2} </math> |
|
<math>~\Rightarrow ~~~~ y(y^2 + 1)</math> |
<math>~=</math> |
<math>~3(y^2+1) - 2y </math> |
|
<math>~\Rightarrow ~~~~ y^3 - 3y^2 + 3y - 3</math> |
<math>~=</math> |
<math>~0 \, .</math> |
|
ASIDE: As is well known and documented — see, for example Wolfram MathWorld or Wikipedia's discussion of the topic — the roots of any cubic equation can be determined analytically. In order to evaluate the root(s) of our particular cubic equation, we have drawn from the utilitarian online summary provided by Eric Schechter at Vanderbilt University. For a cubic equation of the general form, <math>~ay^3 + by^2 + cy + d = 0 \, ,</math> a real root is given by the expression, <math>~ y = p + \{q + [q^2 + (r-p^2)^3]^{1/2}\}^{1/3} + \{q - [q^2 + (r-p^2)^3]^{1/2}\}^{1/3} \, ,</math> where, <math>~p \equiv -\frac{b}{3a} \, ,</math> <math>~q \equiv \biggl[p^3 + \frac{bc-3ad}{6a^2} \biggr] \, ,</math> and <math>~r=\frac{c}{3a} \, .</math> In our particular case, <math>~a =1\, ,</math> <math>~b =-3\, ,</math> <math>~c = +3 \, ,</math> and <math>~d = - 3 \, .</math> Hence, interestingly enough, <math>~p = q = r = + 1 \, ,</math> which implies that the real root is,
(There is also a pair of imaginary roots, but they are irrelevant in the context of our overarching astrophysical discussion.) Just for fun, we also used WolframAlpha's online "cubic equation solver" widget to find the root(s) of our specific cubic equation. The image shown here, on the right, displays the key result that was returned by this WolframAlpha widget. |
The single, real root of this cubic equation is,
<math>~y = 1 + 2^{1/3} \, ,</math>
which corresponds to,
<math>~\Delta = \tan^{-1}(1 + 2^{1/3}) \, .</math>
Hence, over this example interval, the maximum of Srivastava's <math>~\theta_{5F}</math> function — and, hence also, the location at which the function's slope transitions from positive to negative values (denoted by the vertical red line in the above figure) — occurs at,
<math>\xi_\mathrm{crit} \equiv e^{2\tan^{-1}(1+2^{1/3})} = 10.05836783\, .</math>
[Comment by J. E. Tohline on 17 April 2015: As far as I have been able to determine, this analytic prescription of <math>~\xi_\mathrm{crit}</math> has not previously been derived, although, as is made clear in what follows, Murphy (1983) has assessed its value numerically to six significant digits.] This agrees precisely with the determination made by J. O. Murphy (1983) — see the (edited) excerpt from his paper displayed in the following boxed-in image — that the portion of the <math>~\theta_{5F}</math> function that falls in the interval <math>~1 \le \xi < \xi_\mathrm{crit}</math> (the segment of the blue curve that lies to the left of the vertical red line in the above figure) is unphysical because the slope of the function is positive throughout that interval.
| Excerpt (edited) from |
|---|
On the other hand, the segment that falls in the interval, <math>~\xi_\mathrm{crit} \le \xi < e^{2\pi}</math> (the segment of the blue curve that lies to the right of the vertical red line in the above figure), can be used to describe the <math>~n=5</math> "envelope" of a bipolytropic configuration because the function value is positive while it's first derivative is negative.
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |