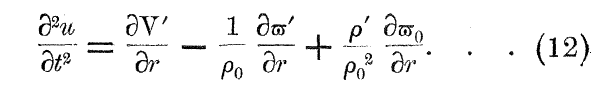Difference between revisions of "User:Tohline/SSC/Stability Eulerian Perspective"
(→Summary and Combinations: Begin inserting Jeans discussion and Bonnor's discussion) |
|||
| Line 386: | Line 386: | ||
<span id="PGE:Euler"><font color="#770000">'''Euler Equation'''</font></span><br /> | <span id="PGE:Euler"><font color="#770000">'''Euler Equation'''</font></span><br /> | ||
<math> | <math> | ||
~\frac{\partial \vec{v}}{\partial t} = - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 | ~\frac{\partial \vec{v}}{\partial t} = - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 \, , | ||
</math><br /> | </math><br /> | ||
| Line 414: | Line 414: | ||
=====James Jeans (1902)===== | =====James Jeans (1902)===== | ||
James H. Jeans [http://adsabs.harvard.edu/abs/1902RSPTA.199....1J (1902, Philosophical Transactions of the royal Society of London. Series A, 199, 1)] used precisely this type of perturbation and linearization analysis when he first derived what is now commonly referred to as the ''Jeans Instability.'' <!-- — quoting from p. 112 of [[User:Tohline/Appendix/References#Shu92|Shu92]], "… [the Jeans criterion for gravitational stability] constitutes perhaps the most frequently cited result of instability theory in all of astronomy." --> For example, if our discussion is restricted only to fluctuations in the radial coordinate direction of a spherically symmetric configuration — in which case <math>~\nabla \rightarrow \partial/\partial r</math> and <math>\vec{v} \rightarrow \hat\mathbf{e}_r \cdot \vec{v} = v_r</math> — our expression for the linearized Euler equation exactly matches equation (12) from Jeans (1902), which, for purposes of illustration, is displayed in the following framed image. | |||
<div align="center"> | <div align="center"> | ||
<table border="2" cellpadding="10" width="75%"> | <table border="2" cellpadding="10" width="75%"> | ||
| Line 429: | Line 429: | ||
<tr> | <tr> | ||
<td align="left"> | <td align="left"> | ||
The correspondence between the righthand-sides of equation (12) from [http://adsabs.harvard.edu/abs/1902RSPTA.199....1J Jeans (1902)] and our derived expression | The correspondence between the righthand-sides of equation (12) from [http://adsabs.harvard.edu/abs/1902RSPTA.199....1J Jeans (1902)] and our derived expression for the linearized Euler equation is clear after accepting the following variable mappings: | ||
<table border="0" align="center" cellpadding="5"> | <table border="0" align="center" cellpadding="5"> | ||
<tr> | <tr> | ||
<td align="right"><math>~ | <td align="right"><math>~V'</math></td> | ||
<td align="center"> <math>~~~ \rightarrow ~~</math> </td> | <td align="center"> <math>~~~ \rightarrow ~~</math> </td> | ||
<td align="left"><math>~ | <td align="left"><math>~- \Phi_1</math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Line 444: | Line 444: | ||
<td align="right"><math>~\varpi'</math></td> | <td align="right"><math>~\varpi'</math></td> | ||
<td align="center"> <math>~~~ \rightarrow ~~</math> </td> | <td align="center"> <math>~~~ \rightarrow ~~</math> </td> | ||
<td align="left"><math>~ | <td align="left"><math>~P_1</math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"><math>~\rho'</math></td> | <td align="right"><math>~\rho'</math></td> | ||
<td align="center"> <math>~~~ \rightarrow ~~</math> </td> | <td align="center"> <math>~~~ \rightarrow ~~</math> </td> | ||
<td align="left"><math>~ | <td align="left"><math>~\rho_1</math></td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
The lefthand side of equation (12) from Jeans (1902) also matches the lefthand side of | The lefthand side of equation (12) from Jeans (1902) also matches the lefthand side of our linearized Euler equation, although this may not be immediately apparent. In the paper by Jeans, <math>~u</math> is not a component of the velocity vector but is, rather, the radial displacement of a fluid element. Hence, | ||
<table border="0" align="center" cellpadding="5"> | <table border="0" align="center" cellpadding="5"> | ||
<tr> | <tr> | ||
<td align="right"><math>~\frac{\partial u}{\partial t | <td align="right"><math>~\frac{\partial u}{\partial t}</math></td> | ||
<td align="center"> <math>~~~ \rightarrow ~~</math> </td> | <td align="center"> <math>~~~ \rightarrow ~~</math> </td> | ||
<td align="left"><math>~ | <td align="left"><math>~v_r</math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"><math>~\Rightarrow~~~\frac{\partial^2 u}{\partial t^2 | <td align="right"><math>~\Rightarrow~~~\frac{\partial^2 u}{\partial t^2} </math></td> | ||
<td align="center"> <math>~~~ \rightarrow ~~</math> </td> | <td align="center"> <math>~~~ \rightarrow ~~</math> </td> | ||
<td align="left"><math>~\frac{\partial | <td align="left"><math>~\frac{\partial v_r}{\partial t} </math></td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| Line 470: | Line 470: | ||
</div> | </div> | ||
=====Bonnor (1957)===== | =====W. B. Bonnor (1957)===== | ||
Above, in our opening layout of the governing equations and supplemental relations, we pointed out that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 488: | Line 488: | ||
</table> | </table> | ||
</div> | </div> | ||
If | If we make this substitution in our linearized Euler equation, and also use the linearized first law of thermodynamics to replace <math>~P_1</math> in favor of <math>~\rho_1</math>, we obtain, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
Revision as of 22:19, 9 December 2014
Stability of Spherically Symmetric Configurations (Eulerian Perspective)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
A standard technique that is used throughout astrophysics to test the stability of self-gravitating fluids involves perturbing physical variables away from their initial (usually equilibrium) values then linearizing each of the principal governing equations before seeking solutions describing the time-dependent behavior of the variables that simultaneously satisfy all of the equations. When the effects of the fluid's self gravity are ignored and this analysis technique is applied to an initially homogeneous medium, the combined set of linearized governing equations generates a wave equation that governs the propagation of sound waves. Here we build on our separate, introductory discussion of sound waves and apply standard perturbation & linearization techniques to spherically symmetric, inhomogeneous and self-gravitating fluids. We will assume that the reader has read this separate introductory discussion and, in particular, understands how the linear wave equation that governs the propagation of sound waves is derived from the set of nonlinear, principal governing equations.
Assembling the Key Relations
Governing Equations and Supplemental Relations
We begin with the set of principal governing equations that provides the foundation for all of our discussions in this H_Book, namely, the
Eulerian Representation
of the Continuity Equation,
<math>~\frac{\partial\rho}{\partial t} + \nabla \cdot (\rho \vec{v}) = 0</math>
Eulerian Representation
of the Euler Equation,
<math>~\frac{\partial\vec{v}}{\partial t} + (\vec{v}\cdot \nabla) \vec{v}= - \frac{1}{\rho} \nabla P - \nabla \Phi</math>
Adiabatic Form of the
First Law of Thermodynamics
<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math> .
Poisson Equation
|
<math>\nabla^2 \Phi = 4\pi G \rho</math> |
As was done in our separate, introductory discussion of sound waves, we will assume that we are dealing with an ideal gas and supplement this set of equations with a barotropic (polytropic) equation of state,
<math>~P = K\rho^{\gamma_\mathrm{g}}</math> … with … <math>\gamma_\mathrm{g} \equiv \frac{d\ln P_0}{d\ln \rho_0} = \frac{\rho_0}{P_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \, ,</math>
which will ensure that the adiabatic form of the first law of thermodynamics is satisfied. When we develop the linearized Euler equation, below, it will be useful to recognize that, assuming <math>~\gamma_\mathrm{g}</math> is uniform throughout the fluid, we can rewrite this last expression as,
|
<math>~\frac{\nabla P_0}{P_0}</math> |
<math>~=</math> |
<math>~\biggl[\frac{\rho_0}{P_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \frac{\nabla \rho_0}{\rho_0}</math> |
|
<math>~\Rightarrow ~~~ \nabla P_0</math> |
<math>~=</math> |
<math>~\biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 \, .</math> |
Perturbation then Linearization of Equations
In this Eulerian analysis, we are investigating how conditions vary with time at a fixed point in space, <math>~\vec{r}</math>. By analogy with our separate introductory analysis of sound waves, we will write the four primary variables in the form,
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_0(\vec{r}) + \rho_1(\vec{r},t) \, ,</math> |
|
<math>~\vec{v}</math> |
<math>~=</math> |
<math>~\cancelto{0}{\vec{v}_0} + \vec{v}_1(\vec{r},t) = \vec{v}(\vec{r},t) \, ,</math> |
|
<math>~P</math> |
<math>~=</math> |
<math>~P_0(\vec{r}) + P_1(\vec{r},t) \, ,</math> |
|
<math>~\Phi</math> |
<math>~=</math> |
<math>~\Phi_0(\vec{r}) + \Phi_1(\vec{r},t) \, ,</math> |
where quantities with subscript "0" are initial values — independent of time, but not necessarily spatially uniform, and usually specified via some choice of an initial equilibrium configuration — and quantities with subscript "1" denote variations away from the initial state, which are assumed to be small in amplitued — for example, <math>~|\rho_1/\rho_0 | \ll 1</math> and <math>~| P_1/P_0 | \ll 1</math>. As indicated, we will assume that the fluid configuration is initially stationary <math>~(\mathrm{i.e.,}~\vec{v}_0 = 0)</math> and, for simplicity, will not append the subscript "1" to the velocity perturbation. It is to be understood, however, that the velocity, <math>~\vec{v}</math>, is small also. In what follows, by definition, <math>~P_1</math>, <math>~\rho_1</math>, <math>~\Phi_1</math>, and <math>~\vec{v}</math> are considered to be of first order in smallness, while products of these quantities are of second (or even higher) order in smallness.
Continuity Equation
Substituting the expression for <math>~\rho</math> into the lefthand side of the continuity equation and neglecting small quantities of the second order, we have,
|
<math>~~\frac{\partial}{\partial t} (\rho_0 + \rho_1) + \nabla\cdot [(\rho_0 + \rho_1)\vec{v}]</math> |
<math>~=</math> |
<math>~ \cancelto{0}{\frac{\partial \rho_0}{\partial t}} + \frac{\partial \rho_1}{\partial t} + \nabla\cdot (\rho_0 \vec{v}) + \nabla\cdot\cancelto{\mathrm{small}}{(\rho_1\vec{v} )} </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{\partial \rho_1}{\partial t} + \rho_0\nabla\cdot \vec{v} + \vec{v}\cdot \nabla\rho_0 \, , </math> |
where, in the first line, the first term on the lefthand side has been set to zero because <math>~\rho_0</math> is independent of time. Hence, we have the desired,
Linearized Continuity Equation
|
<math>~ \frac{\partial \rho_1}{\partial t} + \rho_0\nabla\cdot \vec{v} + \vec{v}\cdot \nabla\rho_0 </math> |
<math>~=</math> |
<math>~0 \, .</math> |
Note that, if we were to assume that the initial configuration is homogeneous, then we could set <math>~\nabla\rho_0 = 0</math> and drop the last term on the righthand side of this expression, retrieving the linearized continuity equation used in our introductory discussion of sound waves.
Euler Equation
Next, we turn to the Euler equation and note that the term,
|
<math>(\vec{v} \cdot \nabla)\vec{v} \, ,</math> |
may be altogether neglected because it is of second order in smallness. Substituting the expressions for <math>~\rho</math>, <math>~P</math>, and <math>~\Phi</math> into the righthand side of the Euler equation and neglecting small quantities of the second order, we have,
|
<math>~- \frac{1}{(\rho_0 + \rho_1)} \nabla (P_0 + P_1) - \nabla(\Phi_0 + \Phi_1)</math> |
<math>~=</math> |
<math>~- \frac{1}{\rho_0} \biggl( 1 + \frac{\rho_1}{\rho_0} \biggr)^{-1} \biggl[ \nabla P_0 + \nabla P_1\biggr] - \nabla(\Phi_0 + \Phi_1) </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\rho_0} \biggl[ 1 - \frac{\rho_1}{\rho_0} + \cancelto{\mathrm{small}}{\biggl(\frac{\rho_1}{\rho_0} \biggr)^2} + \cdots \biggr] \biggl[ \nabla P_0 + \nabla P_1\biggr] - \nabla(\Phi_0 + \Phi_1) </math> |
|
|
<math>~=</math> |
<math>~ - \cancelto{0}{\biggl[ \frac{1}{\rho_0} \nabla P_0 + \nabla \Phi_0 \biggr]} -\frac{1}{\rho_0} \nabla P_1 - \nabla\Phi_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 + \frac{1}{\rho_0^2} \cancelto{\mathrm{small}}{(\rho_1 \nabla P_1)} \, , </math> |
where, the binomial theorem has been used to obtain the expression on the righthand side of the second line and, in the last line, the sum of the first pair of terms has been set to zero because the initial configuration is assumed to be in equilibrium. Combining these simplification steps, we have the,
Linearized Euler Equation
|
<math>~ \frac{\partial \vec{v}}{\partial t} </math> |
<math>~=</math> |
<math>~ - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 - \nabla\Phi_1 \, . </math> |
Ultimately, as emphasized in LL75, the condition that the linearized governing equations should be applicable to the propagation of sound waves is that the velocity of the fluid particles in the wave should be small compared with the velocity of sound, that is, <math>~|\vec{v}| \ll c_s</math>.
First Law of Thermodynamics
In a similar fashion, perturbing the variables in the barotropic equation of state leads to,
|
<math>~ P_0 + P_1 </math> |
<math>~=</math> |
<math>~ K (\rho_0 + \rho_1)^{\gamma_\mathrm{g}} </math> |
|
|
<math>~=</math> |
<math>~ K\rho_0^{\gamma_\mathrm{g}} \biggl(1 + \frac{\rho_1}{\rho_0} \biggr)^{\gamma_\mathrm{g}} </math> |
|
<math>~\Rightarrow~~~ P_1</math> |
<math>~=</math> |
<math>~ K\rho_0^{\gamma_\mathrm{g}} \biggl(1 + \frac{\rho_1}{\rho_0} \biggr)^{\gamma_\mathrm{g}} - K\rho_0^{\gamma_\mathrm{g}} </math> |
|
|
<math>~=</math> |
<math>~ K\rho_0^{\gamma_\mathrm{g}} \biggl[1 + \gamma_\mathrm{g}\biggl(\frac{\rho_1}{\rho_0} \biggr) + \frac{\gamma_\mathrm{g}(\gamma_\mathrm{g}-1)}{2} \cancelto{\mathrm{small}}{\biggl(\frac{\rho_1}{\rho_0} \biggr)^2} + \cdots \biggr] - K\rho_0^{\gamma_\mathrm{g}} </math> |
|
|
<math>~\approx</math> |
<math>~ \gamma_\mathrm{g} \biggl( \frac{P_0}{\rho_0} \biggr) \rho_1 \, . </math> |
Hence, as in our separate introductory discussion of sound waves, we have the,
Linearized Equation of State
|
<math>~P_1</math> |
<math>~=</math> |
<math>~ \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1\, . </math> |
Summary and Combinations
In summary, the following four linearized equations govern the time-dependent physical relationship between the three perturbation amplitudes <math>~P_1(\vec{r},t)</math>, <math>~\rho_1(\vec{r},t)</math>, <math>~\Phi_1(\vec{r},t)</math> and <math>~\vec{v}(\vec{r},t)</math> in self-gravitating fluids:
|
Linearized Linearized Linearized <math> P_1 = \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1\, , </math> Linearized <math> \nabla^2 \Phi_1 = 4\pi G \rho_1\, . </math> |
Simplification to Match Sound-Waves
This set of linearized governing equations is more general than the set of equations that has traditionally been used to describe the propagation of sound waves. The equations governing sound-wave propagation can be retrieved by choosing an initially homogeneous medium — in which case, <math>~\nabla\rho_0 = 0</math> and <math>~\nabla P_0 = 0</math> — and by ignoring the fluid's self gravity, that is, by setting <math>~\Phi_1 = 0</math>.
Comparison with Classic Research Publications
James Jeans (1902)
James H. Jeans (1902, Philosophical Transactions of the royal Society of London. Series A, 199, 1) used precisely this type of perturbation and linearization analysis when he first derived what is now commonly referred to as the Jeans Instability. For example, if our discussion is restricted only to fluctuations in the radial coordinate direction of a spherically symmetric configuration — in which case <math>~\nabla \rightarrow \partial/\partial r</math> and <math>\vec{v} \rightarrow \hat\mathbf{e}_r \cdot \vec{v} = v_r</math> — our expression for the linearized Euler equation exactly matches equation (12) from Jeans (1902), which, for purposes of illustration, is displayed in the following framed image.
|
Linearized Euler Equation as Derived and Presented by Jeans (1902) |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
The correspondence between the righthand-sides of equation (12) from Jeans (1902) and our derived expression for the linearized Euler equation is clear after accepting the following variable mappings:
The lefthand side of equation (12) from Jeans (1902) also matches the lefthand side of our linearized Euler equation, although this may not be immediately apparent. In the paper by Jeans, <math>~u</math> is not a component of the velocity vector but is, rather, the radial displacement of a fluid element. Hence,
|
W. B. Bonnor (1957)
Above, in our opening layout of the governing equations and supplemental relations, we pointed out that,
|
<math>~\nabla P_0</math> |
<math>~=</math> |
<math>~\biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 \, .</math> |
If we make this substitution in our linearized Euler equation, and also use the linearized first law of thermodynamics to replace <math>~P_1</math> in favor of <math>~\rho_1</math>, we obtain,
|
<math>~\frac{\partial \vec{v}}{\partial t} </math> |
<math>~=</math> |
<math>~- \nabla\Phi_1 - \frac{1}{\rho_0} \nabla\biggl[ \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1\biggr] + \frac{\rho_1}{\rho_0^2} \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 </math> |
|
|
<math>~=</math> |
<math>~- \nabla\Phi_1 - \frac{1}{\rho_0} \nabla\biggl[ \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1\biggr] - \rho_1 \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \biggl(\frac{1}{\rho_0} \biggr) </math> |
|
|
<math>~=</math> |
<math>~- \nabla\Phi_1 - \nabla\biggl[\frac{\rho_1}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] </math> |
Wave Equation Derivation
It is customary to combine these three relations to obtain a single, second-order partial-differential equation in terms of (any) one of the perturbation amplitudes. We begin by using the third equation to replace <math>~P_1</math> in favor of <math>~\rho_1</math> in the second equation. This generates,
|
<math>~ \rho_0 \frac{\partial \vec{v}}{\partial t} + \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_1 </math> |
<math>~=</math> |
<math>~ 0 \, . </math> |
Taking the divergence of this equation gives,
|
<math>~ \rho_0 \frac{\partial}{\partial t}(\nabla\cdot \vec{v}) + \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla^2 \rho_1 </math> |
<math>~=</math> |
<math>~ 0 \, ; </math> |
while taking the time derivative of the first (i.e., the linearized continuity) equation gives,
|
<math>~ \frac{\partial^2 \rho_1}{\partial t^2} + \rho_0 \frac{\partial}{\partial t}(\nabla\cdot \vec{v}) </math> |
<math>~=</math> |
<math>~0 \, .</math> |
(Note that we have freely interchanged the order of the <math>~\nabla</math> and <math>~\partial/\partial t</math> operators because the spatial operator is not a function of time. Also, as before, quantities having a subscript "0" have been pulled outside of both operators because, in this discussion, they have no time- or spatial-dependence.) Finally, taking the difference between these last two relations produces the anticipated,
|
Wave Equation <math>~ \frac{\partial^2 \rho_1}{\partial t^2} - c_s^2 \nabla^2 \rho_1 = 0 </math> |
exhibiting the wave propagation speed,
<math>~ c_s = \sqrt{\biggl( \frac{dP}{d\rho} \biggr)_0} \, . </math>
As derived, this wave equation describes, from an Eulerian (as opposed to Lagrangian) perspective, how the density perturbation, <math>~\rho_1(\vec{r},t)</math>, varies with time at any coordinate position.
Alternatives
Utilizing the linearized adiabatic form of the first law of thermodynamics, we can trivially replace <math>~\rho_1</math> with <math>~P_1</math> in the above wave equation to obtain a
|
Wave Equation <math>~ \frac{\partial^2 P_1}{\partial t^2} - c_s^2 \nabla^2 P_1 = 0 \, , </math> |
that exhibits the same wave propagation speed but describes the variation of the pressure, rather than density, fluctuations. Alternatively, adopting the approach preferred by LL75, we can introduce the velocity potential by putting,
<math>\vec{v} = \nabla\phi \, ,</math>
in the linearized governing equations. After also replacing <math>~P_1</math> in favor of <math>~\rho_1</math> in the linearized Euler equation, we have,
|
<math>~\rho_0 \frac{\partial \nabla\phi}{\partial t} + \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_1</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~ \Rightarrow ~~~ \nabla \biggl[ \rho_0 \frac{\partial \phi}{\partial t} + \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1 \biggr] </math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~ \Rightarrow ~~~ \frac{\partial \phi}{\partial t} + \frac{1}{\rho_0}\biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1 </math> |
<math>~=</math> |
<math>~0 \, .</math> |
Taking the time-derivative of this expression gives,
|
<math>~\frac{1}{\rho_0} \frac{\partial \rho_1}{\partial t} + \biggl( \frac{dP}{d\rho} \biggr)_0^{-1} \frac{\partial^2 \phi}{\partial t^2} </math> |
<math>~=</math> |
<math>~ 0 \, .</math> |
In addition, the linearized continuity equation becomes,
<math> \frac{1}{\rho_0} \frac{\partial \rho_1}{\partial t} + \nabla^2 \phi = 0 . </math>
Taking the difference between these last two expressions generates a (see, also, equation 63.7 of LL75),
|
Wave Equation <math>~ \frac{\partial^2 \phi}{\partial t^2} - c_s^2 \nabla^2 \phi = 0 \, , </math> |
that exhibits the same wave propagation speed but describes the variation of the velocity potential, rather than density or pressure fluctuations.
See Also
- Part II of Spherically Symmetric Configurations: Stability
- Wave Equation
- Sound Waves and Gravitational Instability — class notes provided online by David H. Weinberg (The Ohio State University)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |