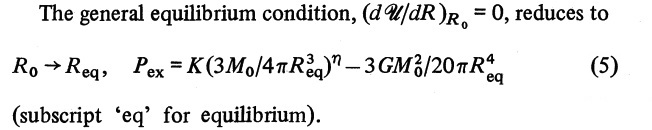Difference between revisions of "User:Tohline/SSC/Structure/StahlerMassRadius"
(Begin separate chapter discussion Staher's (1983) mass-radius relationship for n=5 embedded polytropes) |
(→Stahler's Mass-Radius Relationship for Embedded Polytropes: Significant derivation, trying to compare with Stahler's mass-radius relation) |
||
| Line 3: | Line 3: | ||
=Stahler's Mass-Radius Relationship for Embedded Polytropes= | =Stahler's Mass-Radius Relationship for Embedded Polytropes= | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
==Review== | |||
In [[User:Tohline/SSC/Structure/PolytropesEmbedded#Embedded_Polytropic_Spheres|an accompanying chapter that discusses detailed force-balanced models of embedded (and pressure-truncated) polytropes]], we review [http://adsabs.harvard.edu/abs/1983ApJ...268..165S S. W. Stahler's (1983)] pair of parametric [[User:Tohline/SSC/Structure/PolytropesEmbedded#Stahler.27s_Presentation|relations for the equilibrium mass and equilibrium radius]] for such systems, namely, | In [[User:Tohline/SSC/Structure/PolytropesEmbedded#Embedded_Polytropic_Spheres|an accompanying chapter that discusses detailed force-balanced models of embedded (and pressure-truncated) polytropes]], we review [http://adsabs.harvard.edu/abs/1983ApJ...268..165S S. W. Stahler's (1983)] pair of parametric [[User:Tohline/SSC/Structure/PolytropesEmbedded#Stahler.27s_Presentation|relations for the equilibrium mass and equilibrium radius]] for such systems, namely, | ||
<div align="center"> | <div align="center"> | ||
| Line 74: | Line 76: | ||
</div> | </div> | ||
In what was intended to be a complementary discussion, our [[User:Tohline/SSC/Virial/Polytropes#Nonrotating_Adiabatic_Configuration_Embedded_in_an_External_Medium|free-energy analysis of embedded polytropes]] produced a virial equilibrium expression of the general form, | |||
<div align="center"> | |||
<math> | |||
\mathcal{A} - \mathcal{B}\chi_\mathrm{eq}^{4 -3\gamma_g} +~ \mathcal{D}\chi_\mathrm{eq}^4 = 0 \, , | |||
</math> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{R_\mathrm{eq}}{R_\mathrm{norm}} | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | |||
\frac{1}{\tilde\mathfrak{f}_M} \biggr]^2 \cdot \tilde\mathfrak{f}_W \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} | |||
\cdot \tilde\mathfrak{f}_A \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \biggl( \frac{G}{K} \biggr) M_\mathrm{tot}^{2-\gamma_g} \biggr]^{1/(4-3\gamma_g)} | |||
=\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{1/(n-3)} | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{K^4}{G^{3\gamma_g} M_\mathrm{tot}^{2\gamma_g}} \biggr]^{n/(n-3)} | |||
= \biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and, | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center" colspan="1"> | |||
Structural Form Factors for <font color="red">Pressure-Truncated</font> Polytropes | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tilde\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\tilde\xi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\tilde\xi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_A </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\tilde\xi} + \tilde\Theta^{n+1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
When we went back to compare the mass-radius relationship that results from our very general virial equilibrium expression to the one published by Stahler for pressure-truncated <math>~n = 5</math> polytropes, they did not appear to agree. In what follows, we methodically plow through this comparison in considerable detail to uncover whatever discrepancies might exist. | |||
==Comparison== | |||
First, let's insert the definitions of the coefficients <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{C}</math> into the virial equilibrium expression, replacing, where necessary, the adiabatic exponent in favor of the polytropic index, using the relation, <math>~\gamma_g = (n+1)/n</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathcal{A} - \mathcal{B}\chi_\mathrm{eq}^{(n-3)/n} +~ \mathcal{D}\chi_\mathrm{eq}^4</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | |||
\frac{1}{\tilde\mathfrak{f}_M} \biggr]^2 \cdot \tilde\mathfrak{f}_W | |||
~-~ \frac{4\pi}{3} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} | |||
\cdot \tilde\mathfrak{f}_A \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr)^{(n-3)/n} | |||
+~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr) ^4 | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Next, explicitly spelling out as well the definitions of our adopted normalization radius and normalization pressure — recognizing that <math>~P_\mathrm{norm} R_\mathrm{norm}^4 = GM^2_\mathrm{tot}</math> — and multiply the expression through by <math>[3GM_\mathrm{tot}^2/(4\pi)]</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{20\pi} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) GM_\mathrm{limit}^2 | |||
~-~ GM_\mathrm{tot}^2 | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \biggr]_\mathrm{eq}^{(n+1)/n} | |||
\biggl[ \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{(n+1)/n}} \biggr] | |||
\biggl[ \biggl( \frac{K}{G} \biggr) M_\mathrm{tot}^{(1-n)/n} \biggr] R_\mathrm{eq}^{(n-3)/n} | |||
+~ P_e R_\mathrm{eq}^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{20\pi} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) GM_\mathrm{limit}^2 | |||
~-~ K | |||
\biggl[ \frac{3}{4\pi} \cdot \frac{M_\mathrm{limit}}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} \mathfrak{f}_A | |||
R_\mathrm{eq}^{(n-3)/n} | |||
+~ P_e R_\mathrm{eq}^4 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
As has been pointed out in our separate, [[User:Tohline/SSC/Virial/Polytropes#Solution_Expressed_in_Terms_of_K_and_M_.28Whitworth.27s_1981_Relation.29|more general discussion of the virial equilibrium of polytropes]], if we multiply this expression through by <math>~R_\mathrm{eq}^{-4}</math>, set all three structural form factors, <math>~\mathfrak{f}_i</math>, equal to unity, and replace <math>~M_\mathrm{limit}</math> with the notation, <math>~M_0</math>, the expression exactly matches the one presented as equation (5) of [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth], which reads: | |||
<div align="center"> | |||
<table border="2"> | |||
<tr><td> | |||
[[File:Whitworth1981Eq5.jpg|500px|center|Whitworth (1981, MNRAS, 195, 967)]] | |||
</td></tr> | |||
</table> | |||
</div> | |||
But I like this last version of our derived expression as well because it shows some resemblance to the mass-radius relationship presented by Stahler and highlighted above: The first term on the left-hand-side is a constant times the square of the mass; the third term is a constant times the fourth power of the equilibrium radius; and the middle term shows a cross-product of the mass and radius (in our case, each is raised to a power other than unity). In an effort to make the comparison with Stahler even clearer, let's rewrite our expression in terms of the mass and equilibrium radius, normalized respectively to <math>~M_\mathrm{SWS}</math> and <math>~R_\mathrm{SWS}</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3G}{20\pi} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 | |||
\biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^2 | |||
~+~ P_e \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~-~ K \mathfrak{f}_A | |||
\biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} | |||
\biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{(n+1)/n} | |||
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^{(n-3)/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr)^{3} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 | |||
\biggl[ K_n^{4n} P_\mathrm{e}^{(3-n)} \biggr]^{1/(n+1)} G^{-2} | |||
~+~ \biggl( \frac{n+1}{n} \biggr)^{2} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \biggl[ K_n^{4n} P_\mathrm{e}^{[(n+1)+2(1-n)]} \biggr]^{1/(n+1)} G^{-2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~-~\mathfrak{f}_A | |||
\biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{n+1}{nG} \biggr)^{[3(n+1)+(n-3)]/2n} | |||
\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} | |||
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} | |||
\biggl[ K^{1 + 2 + (n-3)/(n+1)} \biggr] \biggl[ P_\mathrm{e}^{(3-n) + (1-n)(n-3)/(n+1) } \biggr]^{1/(2n)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr)^{3} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 | |||
\biggl[ K_n^{4n} P_\mathrm{e}^{(3-n)} \biggr]^{1/(n+1)} G^{-2} | |||
~+~ \biggl( \frac{n+1}{n} \biggr)^{2} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \biggl[ K_n^{4n} P_\mathrm{e}^{(3-n)} \biggr]^{1/(n+1)} G^{-2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~-~\mathfrak{f}_A | |||
\biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{n+1}{n} \biggr)^{2} | |||
\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} | |||
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} | |||
\biggl[ K^{4n/(n+1)} \biggr] \biggl[ P_\mathrm{e}^{(3-n)/(n+1) } \biggr] G^{-2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 | |||
~-~\mathfrak{f}_A | |||
\biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} | |||
\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} | |||
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} | |||
~+~ \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 00:01, 30 September 2014
Stahler's Mass-Radius Relationship for Embedded Polytropes

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Review
In an accompanying chapter that discusses detailed force-balanced models of embedded (and pressure-truncated) polytropes, we review S. W. Stahler's (1983) pair of parametric relations for the equilibrium mass and equilibrium radius for such systems, namely,
|
<math> ~M </math> |
<math>~=~</math> |
<math> M_\mathrm{SWS} \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \biggl\{ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr\}_{\xi_e} </math> |
|
<math> ~R_\mathrm{eq} </math> |
<math>~=~</math> |
<math> R_\mathrm{SWS} \biggl( \frac{n}{4\pi} \biggr)^{1/2} \biggl\{ \xi \theta_n^{(n-1)/2} \biggr\}_{\xi_e} </math> |
where,
<math>M_\mathrm{SWS} = \biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math>
<math> R_\mathrm{SWS} = \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, , </math>
and point out that Stahler (1983) (see his equation B13) explicitly states that the relevant mass-radius relationship for <math>~n = 5</math> embedded polytropes is,
|
<math> \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^2 - 5 \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) + \frac{20\pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 </math> |
<math>~=~</math> |
<math> ~0 \, . </math> |
In what was intended to be a complementary discussion, our free-energy analysis of embedded polytropes produced a virial equilibrium expression of the general form,
<math> \mathcal{A} - \mathcal{B}\chi_\mathrm{eq}^{4 -3\gamma_g} +~ \mathcal{D}\chi_\mathrm{eq}^4 = 0 \, , </math>
where,
|
<math>~\chi_\mathrm{eq}</math> |
<math>~\equiv</math> |
<math>\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \, ,</math> |
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^2 \cdot \tilde\mathfrak{f}_W \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} \cdot \tilde\mathfrak{f}_A \, , </math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, , </math> |
and,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \biggl( \frac{G}{K} \biggr) M_\mathrm{tot}^{2-\gamma_g} \biggr]^{1/(4-3\gamma_g)} =\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{1/(n-3)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{K^4}{G^{3\gamma_g} M_\mathrm{tot}^{2\gamma_g}} \biggr]^{n/(n-3)} = \biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, ,</math> |
and,
|
Structural Form Factors for Pressure-Truncated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
When we went back to compare the mass-radius relationship that results from our very general virial equilibrium expression to the one published by Stahler for pressure-truncated <math>~n = 5</math> polytropes, they did not appear to agree. In what follows, we methodically plow through this comparison in considerable detail to uncover whatever discrepancies might exist.
Comparison
First, let's insert the definitions of the coefficients <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{C}</math> into the virial equilibrium expression, replacing, where necessary, the adiabatic exponent in favor of the polytropic index, using the relation, <math>~\gamma_g = (n+1)/n</math>.
|
<math>~0</math> |
<math>~=</math> |
<math>~\mathcal{A} - \mathcal{B}\chi_\mathrm{eq}^{(n-3)/n} +~ \mathcal{D}\chi_\mathrm{eq}^4</math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^2 \cdot \tilde\mathfrak{f}_W ~-~ \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} \cdot \tilde\mathfrak{f}_A \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr)^{(n-3)/n} +~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr) ^4 </math> |
Next, explicitly spelling out as well the definitions of our adopted normalization radius and normalization pressure — recognizing that <math>~P_\mathrm{norm} R_\mathrm{norm}^4 = GM^2_\mathrm{tot}</math> — and multiply the expression through by <math>[3GM_\mathrm{tot}^2/(4\pi)]</math>.
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{3}{20\pi} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) GM_\mathrm{limit}^2 ~-~ GM_\mathrm{tot}^2 \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \biggr]_\mathrm{eq}^{(n+1)/n} \biggl[ \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{(n+1)/n}} \biggr] \biggl[ \biggl( \frac{K}{G} \biggr) M_\mathrm{tot}^{(1-n)/n} \biggr] R_\mathrm{eq}^{(n-3)/n} +~ P_e R_\mathrm{eq}^4 </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{20\pi} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) GM_\mathrm{limit}^2 ~-~ K \biggl[ \frac{3}{4\pi} \cdot \frac{M_\mathrm{limit}}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} \mathfrak{f}_A R_\mathrm{eq}^{(n-3)/n} +~ P_e R_\mathrm{eq}^4 \, . </math> |
As has been pointed out in our separate, more general discussion of the virial equilibrium of polytropes, if we multiply this expression through by <math>~R_\mathrm{eq}^{-4}</math>, set all three structural form factors, <math>~\mathfrak{f}_i</math>, equal to unity, and replace <math>~M_\mathrm{limit}</math> with the notation, <math>~M_0</math>, the expression exactly matches the one presented as equation (5) of Whitworth, which reads:
But I like this last version of our derived expression as well because it shows some resemblance to the mass-radius relationship presented by Stahler and highlighted above: The first term on the left-hand-side is a constant times the square of the mass; the third term is a constant times the fourth power of the equilibrium radius; and the middle term shows a cross-product of the mass and radius (in our case, each is raised to a power other than unity). In an effort to make the comparison with Stahler even clearer, let's rewrite our expression in terms of the mass and equilibrium radius, normalized respectively to <math>~M_\mathrm{SWS}</math> and <math>~R_\mathrm{SWS}</math>.
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{3G}{20\pi} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^2 ~+~ P_e \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^4 </math> |
|
|
|
<math>~ ~-~ K \mathfrak{f}_A \biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{(n+1)/n} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^{(n-3)/n} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr)^{3} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 \biggl[ K_n^{4n} P_\mathrm{e}^{(3-n)} \biggr]^{1/(n+1)} G^{-2} ~+~ \biggl( \frac{n+1}{n} \biggr)^{2} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \biggl[ K_n^{4n} P_\mathrm{e}^{[(n+1)+2(1-n)]} \biggr]^{1/(n+1)} G^{-2} </math> |
|
|
|
<math>~ ~-~\mathfrak{f}_A \biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{n+1}{nG} \biggr)^{[3(n+1)+(n-3)]/2n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} \biggl[ K^{1 + 2 + (n-3)/(n+1)} \biggr] \biggl[ P_\mathrm{e}^{(3-n) + (1-n)(n-3)/(n+1) } \biggr]^{1/(2n)} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr)^{3} \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 \biggl[ K_n^{4n} P_\mathrm{e}^{(3-n)} \biggr]^{1/(n+1)} G^{-2} ~+~ \biggl( \frac{n+1}{n} \biggr)^{2} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \biggl[ K_n^{4n} P_\mathrm{e}^{(3-n)} \biggr]^{1/(n+1)} G^{-2} </math> |
|
|
|
<math>~ ~-~\mathfrak{f}_A \biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{n+1}{n} \biggr)^{2} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} \biggl[ K^{4n/(n+1)} \biggr] \biggl[ P_\mathrm{e}^{(3-n)/(n+1) } \biggr] G^{-2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^2 ~-~\mathfrak{f}_A \biggl[ \frac{3}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n+1)/n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} ~+~ \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 </math> |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |