User:Tohline/SSC/VirialStability

Virial Stability of BiPolytropes

BiPolytrope Structural Relations

[Following a discussion that Tohline had with Kundan Kadam on 3 July 2013, we have decided to carry out a virial equilibrium and stability analysis of nonrotating bipolytropes.]

We will adopt the following approach:

• Properties of the core <math>\cdots</math>
  • Uniform density, <math>\rho_c</math>;
  • Polytropic constant, <math>K_c</math>, and polytropic index, <math>n_c</math>;
  • Surface of the core at <math>r_i</math>;
• Properties of the envelope <math>\cdots</math>
  • Uniform density, <math>\rho_e</math>;
  • Polytropic constant, <math>K_e</math>, and polytropic index, <math>n_e</math>;
  • Base of the core at <math>r_i</math> and surface at <math>R</math>.

Use the dimensionless radius,

<math>\xi \equiv \frac{r}{r_i}</math>.

Then, <math>\xi_i = 1</math> and <math>\xi_s \equiv R/r_i</math>.

Expressions for Mass

Inside the core, the expression for the mass interior to any radius, <math>0 \le \xi \le 1</math>, is,

<math>M_\xi = \frac{4\pi}{3} \rho_c r_i^3 \xi^3</math> .

The expression for the mass interior to any position within the envelope, <math>1 \le \xi \le \xi_s</math>, is,

<math>M_\xi = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi^3 - 1) \biggr]</math> .

Hence, the mass of the core, the mass of the envelope, and the total mass are, respectively,

<math> M_\mathrm{core} = \frac{4\pi}{3} \rho_c r_i^3 </math> ;

<math> M_\mathrm{env} = \frac{4\pi}{3} r_i^3 \biggl[\rho_e (\xi_s^3 - 1) \biggr] </math> ;

<math> M_\mathrm{tot} = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi_s^3 - 1) \biggr] </math> .

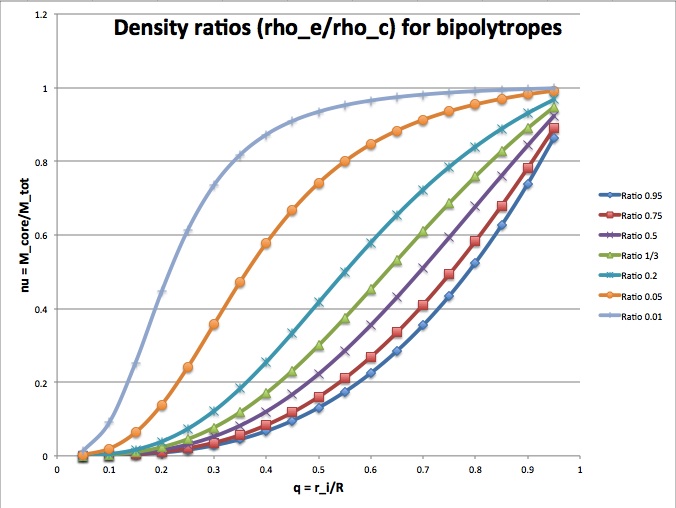
Following the work of Schönberg & Chandrasekhar (1942) — see our accompanying discussion — we are seeking equilibrium configurations in the <math>\nu - q</math> plane where,

<math>\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} </math>     and     <math>q \equiv \frac{r_i}{R} = \frac{1}{\xi_s}</math>.

So we can combine the above expressions to obtain,

<math>\frac{\rho_e}{\rho_c} = \frac{M_\mathrm{env}}{M_\mathrm{core}} (\xi_s^3 - 1)^{-1} = \biggl[ \frac{1-\nu}{\nu}\biggr] (\xi_s^3 - 1)^{-1} = \frac{q^3}{\nu}\biggl( \frac{1 - \nu}{1- q^3} \biggr) \, , </math>

or,

<math>\nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^3} - 1\biggr) \biggr]^{-1}</math> .

It is worth noting that exactly the same result arises from an examination of the analytically definable, structural properties of bipolytropes having <math>n_c = 5</math> and <math>n_e = 1</math>. That is, the ratio of the average density in the envelope to the average density in the core is, <math> \frac{\bar{\rho}_e}{\bar{\rho}_c} = \frac{(M^*_\mathrm{tot} - M^*_\mathrm{core}) / [(R^*)^3 - (r^*_\mathrm{core})^3]}{M^*_\mathrm{core} / (r^*_\mathrm{core})^3 } = \frac{q^3 (1- \nu)}{\nu (1-q^3)} \, . </math> This is, of course, at it should be.

The following figure shows how <math>\nu</math> varies with <math>q</math> for various choices of the mass density ratio, <math>\rho_e/\rho_c</math>. It illustrates that, for a given core-to-total mass ratio, <math>\nu</math>, the relative location of the interface radius, <math>q</math>, can vary between zero and one, but each value of <math>q</math> reflects a different ratio of envelope-to-core mass density.

Energy Expressions

The gravitational potential energy of the bipolytropic configuration is obtained by integrating over the following differential energy contribution,

<math>dW = - \biggl( \frac{GM_r}{r} \biggr) dm</math> .

Hence,

<math>W = W_\mathrm{core} + W_\mathrm{env}</math>	<math> = - G \biggl\{ \int_0^{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_c dr + \int^R_{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_e dr \biggr\} </math>
	<math> = - G \biggl\{ \int_0^1 \biggl( \frac{4\pi }{3} \rho_c r_i^3 \xi^3 \biggr) 4\pi r_i^2 \rho_c \xi d\xi + \int_1^{\xi_s} \frac{4\pi}{3} \rho_c r_i^3 \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] 4\pi r_i^2 \rho_e \xi d\xi \biggr\} </math>
	<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \int_0^1 \xi^4 d\xi + \int_1^{\xi_s} \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] \biggl( \frac{\rho_e}{\rho_c} \biggr) \xi d\xi \biggr\} </math>
	<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \frac{1}{5} + \biggl( \frac{\rho_e}{\rho_c} \biggr) \int_1^{\xi_s} \xi d\xi + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \int_1^{\xi_s} (\xi^3 - 1) \xi d\xi \biggr\} </math>
	<math> = - \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) 3\nu^2 \xi_s \biggl\{ \frac{1}{5} + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{5}(\xi_s^5 - 1) - \frac{1}{2}(\xi_s^2-1) \biggr] \biggr\} </math>
	<math> = - \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \biggl( \frac{R}{R_0}\biggr)^{-1} \nu^2 \xi_s f(\nu,q) \, , </math>

where <math>R_0</math> is an, as yet unspecified, normalization radius, and

<math> f(\nu,q) \equiv 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \, . </math>

I like the form of this expression. The leading term, which scales as <math>R^{-1}</math>, encapsulates the behavior of the gravitational potential energy for a given choice of the internal structure, namely, a given choice of <math>\xi_s</math>, <math>\nu</math>, and density ratio <math>(\rho_e/\rho_c)</math>. Actually, only two internal structural parameters need to be specified — <math>\nu</math> and <math>\xi_s</math> (or, <math>q</math>). From these two, the expression shown above allows the determination of <math>(\rho_e/\rho_c)</math>.

Sanity Check: Uniform Density Configuration <math> M_\mathrm{core} = \frac{4\pi}{3} r_i^3 \rho_c \, ; </math> <math> M_\mathrm{env} = \frac{4\pi}{3} r_i^3 \rho_e (\xi_s^3 -1) \, ; </math> <math> M_\mathrm{tot} = \frac{4\pi}{3} r_i^3 \rho_c \biggl[ 1 + \frac{\rho_e}{\rho_c} (\xi_s^3 -1) \biggr] \, . </math> If <math>\rho_e/\rho_c = 1</math>, then, <math> \frac{M_\mathrm{env}}{M_\mathrm{core}} = \biggl(\frac{1}{\nu} - 1\biggr) = (\xi_s^3 -1) = \biggl(\frac{1}{q^3}-1\biggr) ~~~~\Rightarrow ~~~~ \nu = q^3 \, . </math> The gravitational potential energy is, <math>W\biggr|_{\rho_e/\rho_c = 1}</math> <math> = - \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) 3\nu^2 \xi_s \biggl\{ \frac{1}{5} + \frac{1}{2} (\xi_s^2 - 1) + \biggl[ \frac{1}{5}(\xi_s^5 - 1) - \frac{1}{2}(\xi_s^2-1) \biggr] \biggr\} </math>   <math> = - \frac{3}{5} \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr)\nu^2 \xi_s \biggl\{ \frac{1}{5} + \biggl[ \frac{1}{5}(\xi_s^5 - 1) \biggr] \biggr\} </math>   <math> = - \frac{3}{5} \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr)\nu^2 \xi_s^6 = - \frac{3}{5} \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 = - \frac{3}{5} \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) \, . </math>

Drawing on expressions developed in our introductory discussion of the virial equation, the internal energy of the bipolytropic configuration is,

<math> U = U_\mathrm{core} + U_\mathrm{env} </math>

<math>=</math>

<math> \biggl\{ M_\mathrm{core} \biggl[ (1 - \delta_{\infty n_c}) n_c K_c \rho_c^{1/n_c} + \delta_{\infty n_c} c_s^2 \ln(\rho_c/\rho_0) \biggr] + n_e M_\mathrm{env} K_e \rho_e^{1/n_e} \biggr\} \, , </math>

where <math>\rho_0</math> is an, as yet unspecified, normalization density, and we have allowed for either an isothermal (<math>\delta_{\infty n_c} = 1</math>) or an adiabatic (<math>\delta_{\infty n_c} = 0</math>) core.

Strategy

We want to vary the total radius, <math>R</math>, of the configuration and look for extrema in the free energy, while holding the following parameters fixed: <math>M_\mathrm{tot}</math>, <math>K_e</math>, <math>c_s^2</math> (or <math>K_c</math>), <math>\nu</math>, and <math>q</math>. So we need to rewrite the expressions for <math>W</math> and <math>U</math> such that everything is constant except for <math>R</math>, or <math>\chi \equiv R/R_0</math>. And, in order to put everything explicitly in terms of the fixed parameters just specified, let's go ahead and choose,

<math>R_0 \,</math>	<math>\equiv \,</math>	<math>\frac{GM_\mathrm{tot}}{c_s^2} \, ;</math>
<math>\rho_0 \,</math>	<math>\equiv \,</math>	<math>\frac{3M_\mathrm{tot}}{4\pi R_0^3} = \frac{3M_\mathrm{tot}}{4\pi} \biggl(\frac{GM_\mathrm{tot}}{c_s^2}\biggr)^{-3} = \frac{3}{4\pi} \biggl(\frac{c_s^6}{G^3M^2_\mathrm{tot}}\biggr) \, .</math>

(This particular choice of normalization radius and normalization density won't work for an adiabatic core, but let's understand the structures of models having an isothermal core, first, then deal with the adiabatic core later.) Note also that, because <math>\bar{\rho} \equiv (3M_\mathrm{tot})/(4\pi R^3)</math>, we can write,

<math>\frac{\rho_c}{\bar{\rho}} \,</math>

<math>= \,</math>

<math>\frac{\nu}{q^3} \, ,</math>

<math>\mathrm{and} \,</math>

<math>\frac{\rho_e}{\bar{\rho}} \,</math>

<math>= \,</math>

<math>\frac{1-\nu}{1-q^3} \, .</math>

Energy Expressions

The expression for <math>W</math> shown above needs only a slight modification to put it in the appropriate form, namely,

<math>W \,</math>

<math> = - \frac{3}{5} M_\mathrm{tot} c_s^2 \chi^{-1} \biggl( \frac{\nu^2}{q} \biggr) f(\nu,q) \, , </math>

In the case of an isothermal core, the expression for the total internal energy may be rewritten as,

<math> \frac{U}{M_\mathrm{tot}} \, </math>	<math>= \,</math>	<math> \nu c_s^2 \ln(\rho_c/\rho_0) + (1-\nu) n_e K_e \rho_e^{1/n_e} </math>
	<math>=</math>	<math> \nu c_s^2 [\ln(\rho_c/\bar{\rho}) + \ln(\bar\rho/\rho_0)] + (1-\nu) n_e K_e \rho_0^{1/n_e} \biggl[\biggl( \frac{\rho_e}{\bar\rho} \biggr) \biggl( \frac{\bar\rho}{\rho_0} \biggr) \biggr]^{1/n_e} </math>
	<math>=</math>	<math> \nu c_s^2 [\ln(\nu/q^3) -3 \ln\chi] + (1-\nu) n_e K_e \rho_0^{1/n_e} \biggl( \frac{1-\nu}{1-q^3} \biggr)^{1/n_e} \chi^{-3/n_e} \, . </math>

Hence (in the case of an isothermal core),

<math>\mathfrak{G}</math>	<math>=</math>	<math> - \frac{3}{5} M_\mathrm{tot} c_s^2 \biggl( \frac{\nu^2}{q} \biggr) f(\nu,q) \chi^{-1} + \nu M_\mathrm{tot} c_s^2 [\ln(\nu/q^3) -3 \ln\chi] + (1-\nu) n_e M_\mathrm{tot} K_e \rho_0^{1/n_e} \biggl( \frac{1-\nu}{1-q^3} \biggr)^{1/n_e} \chi^{-3/n_e} </math>
	<math>=</math>	<math> \mathfrak{G}_0 - A \chi^{-1} - C \ln\chi + D \chi^{-3/n_e} \, , </math>

where,

<math>\mathfrak{G}_0 \,</math>	<math>\equiv \,</math>	<math> \nu M_\mathrm{tot} c_s^2 \ln(\nu/q^3) \, , </math>
<math>A \,</math>	<math>\equiv \,</math>	<math> \frac{3}{5} M_\mathrm{tot} c_s^2 \biggl( \frac{\nu^2}{q} \biggr) f(\nu,q) \, , </math>
<math>C \,</math>	<math>\equiv \,</math>	<math> 3 \nu M_\mathrm{tot} c_s^2 \, , </math>
<math>D \, </math>	<math>\equiv \,</math>	<math> (1-\nu) n_e M_\mathrm{tot} K_e \rho_0^{1/n_e} \biggl( \frac{1-\nu}{1-q^3} \biggr)^{1/n_e} = (1-\nu) n_e M_\mathrm{tot} K_e \biggl[ \frac{3}{4\pi} \biggl(\frac{c_s^6}{G^3M^2_\mathrm{tot}}\biggr) \biggr]^{1/n_e} \biggl( \frac{1-\nu}{1-q^3} \biggr)^{1/n_e} \, . </math>

Temperature Across the Interface

In order to ensure that the temperature of the envelope is the same as the temperature of the core when there is a drop in the mean molecular weight at the interface, we need to have,

<math>\biggl[ \frac{P_e}{(\rho_e/\mu_e)}\biggr]_E</math>	<math>= \, </math>	<math>\biggl[ \frac{P_c}{(\rho_c/\mu_c)} \biggr]_E</math>
<math>\Rightarrow ~~~~~ \biggl( \frac{\mu_e}{\mu_c}\biggr) \frac{K_e}{ c_s^2}</math>	<math>= \, </math>	<math>\biggl[\rho_e^{-1/n_e}\biggr]_E</math>
	<math>= \, </math>	<math>\rho_0^{-1/n_e} \biggl[\biggl( \frac{\rho_e}{\bar\rho} \biggr) \biggl( \frac{\bar\rho}{\rho_0} \biggr)_E \biggr]^{-1/n_e}</math>
	<math>= \, </math>	<math> \biggl[ \frac{3}{4\pi} \biggl(\frac{c_s^6}{G^3M^2_\mathrm{tot}}\biggr) \biggr]^{-1/n_e} \biggl( \frac{1-\nu}{1-q^3} \biggr)^{-1/n_e} \biggl( \frac{\bar\rho}{\rho_0} \biggr)_E^{-1/n_e} </math>
<math>\Rightarrow ~~~~~ \chi_E^{3/n_e}</math>	<math>= \, </math>	<math>\biggl( \frac{\mu_e}{\mu_c}\biggr) \frac{K_e}{ c_s^2} \biggl[ \frac{3}{4\pi} \biggl(\frac{c_s^6}{G^3M^2_\mathrm{tot}}\biggr) \biggr]^{1/n_e} \biggl( \frac{1-\nu}{1-q^3} \biggr)^{1/n_e}</math>
	<math>= \, </math>	<math>\biggl( \frac{\mu_e}{\mu_c}\biggr) \biggl[ \frac{D}{(1-\nu)n_e M_\mathrm{tot} c_s^2} \biggr]</math>
	<math>= \, </math>	<math>\biggl( \frac{\mu_e}{\mu_c}\biggr) \biggl[ \frac{3\nu}{(1-\nu)n_e} \biggl(\frac{D}{C}\biggr)\biggr]</math>

Pressure Across the Interface

We will relate <math>K_e</math> to <math>K_c</math> by demanding that initially the pressure is identical in both layers. The relevant algebraic relation will depend on whether the core is isothermal (<math>n_c = \infty</math>), or whether it has a finite polytropic index and therefore adjusts adiabatically to compressions or expansions.

Isothermal Core

Guided by the interface conditions presented in Table 2 of our accompanying discussion of the structure of bipolytropes, the condition for pressure balance in the case of an isothermal core should be,

<math>\frac{c_s^2}{K_e \rho_0^{1/n_e}} = \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e} \biggl( \frac{\rho_e}{\rho_c} \biggr)^{1+1/n_e} = \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{1+1/n_e} \, .</math>

Actually, in the full structural solution,

<math>\frac{c_s^2}{K_e \rho_0^{1/n_e}}</math>	<math>= </math>	<math> \biggl( \frac{\rho_c}{\rho_0} \biggr)^{1/n_e} e^{\psi_i} \biggl( \frac{\rho_e}{\rho_c} \biggr)^{1+1/n_e} \phi_i^{1+n_e} </math>
	<math>= </math>	<math> \biggl( \frac{\rho_c}{\rho_0} \biggr)^{1/n_e} e^{\psi_i} \biggl[ \frac{\mu_e}{\mu_c} e^{-\psi_i} \phi_i^{-{n_e}}\biggr]^{1+1/n_e} \phi_i^{1+n_e} </math>
	<math>= </math>	<math> \biggl( \frac{\rho_c}{\rho_0} e^{-\psi_i} \biggr)^{1/n_e} \biggl[ \frac{\mu_e}{\mu_c} \biggr]^{1+1/n_e} \, . </math>

Adiabatic Core

Guided by the interface conditions presented in Table 2 of our accompanying discussion of the structure of bipolytropes, the condition for pressure balance in the case of polytropic core should be,

<math>\biggl(\frac{K_c}{K_e}\biggr) \rho_0^{1/n_c -1/n_e} = \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e - 1/n_c} \biggl( \frac{\rho_e}{\rho_c} \biggr)^{1+1/n_e} = \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e - 1/n_c} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{1+1/n_e} \, .</math>

Actually, in the full structural solution,

<math>\biggl(\frac{K_c}{K_e}\biggr) \rho_0^{1/n_c -1/n_e} </math>	<math>=</math>	<math> \rho_0^{1/n_c -1/n_e} \rho_c^{-(1+1/n_c)} \theta_i^{-(1+n_c)} \rho_e^{1+1/n_e} \phi_i^{1+n_e} </math>
	<math>=</math>	<math> \biggl( \frac{\rho_c}{\rho_0} \biggr)^{1/n_e - 1/n_c} \theta_i^{-(1+n_c)} \biggl( \frac{\rho_e}{\rho_c}\biggr)^{1+1/n_e} \phi_i^{1+n_e} </math>
	<math>=</math>	<math> \biggl( \frac{\rho_c}{\rho_0} \biggr)^{1/n_e - 1/n_c} \biggl[ \frac{\mu_e}{\mu_c} \theta_i^{n_c} \biggr]^{1+1/n_e} \theta_i^{-(1+n_c)} </math>
	<math>=</math>	<math> \biggl( \frac{\rho_c}{\rho_0} \theta_i^{n_c}\biggr)^{1/n_e - 1/n_c} \biggl[ \frac{\mu_e}{\mu_c} \biggr]^{1+1/n_e} \, . </math>

Virial Analysis

Isothermal Core Equilibrium Condition

For a given set of fixed coefficients in the free energy expression, equilibria are identified by setting <math>\partial\mathfrak{G}/\partial\chi = 0</math>. Generally,

<math>\frac{\partial\mathfrak{G}}{\partial\chi}</math>

<math>= \,</math>

<math> A\chi^{-2} - C\chi^{-1} - \biggl(\frac{3}{n_e}\biggr)D\chi^{-(1+3/n_e)} \, . </math>

So, for the case of <math>n_e = 3/2</math>, the equilibrium radius is given by the condition,

<math>A\chi_E^{-2}</math>	<math>= \,</math>	<math> C\chi_E^{-1} + 2D\chi_E^{-3} </math>
<math> \Rightarrow ~~~~ C\chi_E^{2} - A\chi_E + 2D </math>	<math>= \,</math>	<math>0 \,</math>
<math> \Rightarrow ~~~~ \chi_E </math>	<math>= \,</math>	<math> \frac{1}{2C} \biggl[ A \pm \biggl( A^2 - 8DC \biggr)^{1/2}\biggr] </math>
<math> \Rightarrow ~~~~ \chi_E </math>	<math>= \,</math>	<math> \frac{A}{2C} \biggl[ 1 \pm \biggl( 1 - \frac{8DC}{A^2} \biggr)^{1/2}\biggr] </math>
	<math>= \,</math>	<math> \chi_0 [ 1 \pm \sqrt{1-\Pi} ] \, , </math>

where,

<math>\chi_0 \,</math>

<math>\equiv \,</math>

<math> \frac{A}{2C} \, , </math>

and

<math>\Pi \,</math>

<math>\equiv \,</math>

<math> \frac{8DC}{A^2} \, . </math>

But, from the condition on the temperature at the interface we also need,

<math>\chi_E \,</math>	<math>=\,</math>	<math> \biggl(\frac{\mu_e}{\mu_c} \biggr)^{1/2} \biggl[ \frac{2\nu}{(1-\nu)} \biggl( \frac{D}{C} \biggr)\biggr]^{1/2} </math>
	<math>=\,</math>	<math> \chi_0 \biggl(\frac{\mu_e}{\mu_c} \biggr)^{1/2} \biggl[ \biggl(\frac{\nu}{1-\nu}\biggr) \Pi \biggr]^{1/2} </math>

Free Energy Expression

To within an additive constant, the free energy may now be written as,

<math> \mathfrak{G} = W + U = - A \chi^{-1} + B_e \chi^{-3/n_e} + (1-\delta_{\infty n_c}) B_c \chi^{-3/n_c} - \delta_{\infty n_c} \biggl[ B_I \ln\chi - \frac{1}{3}B_I \ln \biggl( \frac{\rho_c|_0}{\rho_0} \biggr) \biggr] \, , </math>

where, <math>\chi \equiv R/R_0</math> and,

<math> A \, </math>	<math>=\,</math>	<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} = \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \frac{\nu^2}{q} f(\nu, q) \, , </math>
<math>B_e \,</math>	<math>=\,</math>	<math> M_\mathrm{tot}(1-\nu) n_eK_e (\rho_e|_0)^{1/n_e} = M_\mathrm{tot} (1-\nu) K_e\rho_0^{1/n_e} n_e \biggl( \frac{\rho_e|_0}{\rho_0} \biggr)^{1/n_e} \, , </math>
<math>B_c \,</math>	<math>= \,</math>	<math> M_\mathrm{tot} \nu n_c K_c (\rho_c|_0)^{1/n_c} = M_\mathrm{tot} K_e\rho_0^{1/n_e} \nu n_c \biggl[\biggl(\frac{K_c}{K_e}\biggr) \rho_0^{1/n_c - 1/n_e} \biggr] \biggl( \frac{\rho_c|_0}{\rho_0}\biggr)^{1/n_c} = M_\mathrm{tot} K_e\rho_0^{1/n_e} \nu n_c \biggl[ \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e - 1/n_c} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{1+1/n_e} \biggr] \biggl( \frac{\rho_c|_0}{\rho_0}\biggr)^{1/n_c} \, , </math>
<math>B_I\,</math>	<math>=\,</math>	<math> 3 M_\mathrm{tot} c_s^2 \nu = M_\mathrm{tot} K_e\rho_0^{1/n_e} \biggl[ \frac{c_s^2}{K_e\rho_0^{1/n_e} } \biggr] 3\nu = M_\mathrm{tot} K_e\rho_0^{1/n_e} \biggl[ \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{1+1/n_e}\biggr] 3\nu \, . </math>

Derivatives of Free Energy

<math> \frac{\partial\mathfrak{G}}{\partial \chi} = A \chi^{-2} -\frac{3}{n_e} B_e \chi^{-(1+3/n_e)} - (1-\delta_{\infty n_c}) \frac{3}{n_c} B_c \chi^{-(1+3/n_c)} - \delta_{\infty n_c} B_I \chi^{-1} \, ; </math>

<math> \frac{\partial^2\mathfrak{G}}{\partial \chi^2} = -2 A \chi^{-3} + \frac{3}{n_e} \biggl(1+\frac{3}{n_e}\biggr) B_e \chi^{-(2+3/n_e)} + (1-\delta_{\infty n_c}) \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi^{-(2+3/n_c)} + \delta_{\infty n_c} B_I \chi^{-2} \, . </math>

Equilibrium Condition

We obtain the equilibrium radius, <math>\chi_E</math>, when <math>\partial\mathfrak{G}/\partial\chi = 0</math>. Hence, the relation governing the equilibrium radius is,

<math> A \chi_E^{-2} </math>	<math>=</math>	<math> (1-\delta_{\infty n_c}) \frac{3}{n_c} B_c \chi_E^{-1- 3/n_c} +\delta_{\infty n_c} B_I \chi_E^{-1} +\frac{3}{n_e} B_e \chi_E^{-1-3/n_e} </math>
<math> \Rightarrow ~~~~~ \frac{n_e A}{3B_e} </math>	<math>=</math>	<math> (1-\delta_{\infty n_c}) \frac{n_e B_c}{n_c B_e} \chi_E^{1- 3/n_c} +\delta_{\infty n_c} \frac{n_e B_I}{3B_e} \chi_E + \chi_E^{1-3/n_e} </math>
<math> \Rightarrow ~~~~~ \chi_E^{1-3/n_e} </math>	<math>=</math>	<math> \alpha - (1-\delta_{\infty n_c}) \beta \chi_E^{1- 3/n_c} - \delta_{\infty n_c} \beta_I \chi_E \, , </math>

where,

<math>\alpha \,</math>	<math>\equiv \,</math>	<math> \frac{n_e A}{3B_e} = \biggl[ \frac{GM_\mathrm{tot}}{5R_0 K_e (\rho_e|_0)^{1/n_e} } \biggr] \frac{\nu^2 f(\nu, q)}{q} = \biggl[ \frac{GM_\mathrm{tot}}{5R_0 K_e \rho_0^{1/n_e} } \biggr]\biggl( \frac{\rho_e|_0}{\rho_0} \biggr)^{-1/n_e} \frac{\nu^2 f(\nu, q)}{q} \, ; </math>
<math>\beta \,</math>	<math>\equiv \,</math>	<math>\frac{n_e B_c}{n_c B_e} = \nu \biggl[ \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e - 1/n_c} \biggl( \frac{\rho_c|_0}{\rho_0}\biggr)^{1/n_c} \biggl( \frac{\rho_e|_0}{\rho_0} \biggr)^{-1/n_e} \biggr] \biggl( \frac{\mu_e}{\mu_c} \biggr)^{1+1/n_e} \, ; </math>
<math>\beta_I \,</math>	<math>\equiv \,</math>	<math> \frac{n_e B_I}{3B_e} = \frac{c_s^2 \nu}{(1-\nu)K_e (\rho_e|_0)^{1/n_e}} = \nu \biggl[ \biggl(\frac{\rho_c}{\rho_0}\biggr)^{1/n_e} \biggl( \frac{\rho_e|_0}{\rho_0} \biggr)^{-1/n_e} \biggr] \biggl( \frac{\mu_e}{\mu_c} \biggr)^{1+1/n_e} \, . </math>

Isothermal Core

In the case of an isothermal core (<math>\delta_{\infty n_c} = 1</math>),

<math> A \chi_E^{-2} </math>	<math>=</math>	<math> B_I \chi_E^{-1} +\frac{3}{n_e} B_e \chi_E^{-1-3/n_e} </math>
<math> \Rightarrow ~~~~ B_I \chi_E^{3/n_e} - A \chi_E^{3/n_e-1} +\frac{3}{n_e} B_e </math>	<math>=\,</math>	<math> 0 \, . </math>

Or, alternatively, via a dimensionless treatment,

<math> \chi_E^{1-3/n_e} </math>

<math>=</math>

<math> \alpha - \beta_I \chi_E \, . </math>

Adiabatic Core

In the case of an adiabatice core (<math>\delta_{\infty n_c} = 0</math>),

<math> \chi_E^{1-3/n_e} </math>

<math>=</math>

<math> \alpha - \beta \chi_E^{1- 3/n_c} \, . </math>

Stability

At this equilibrium radius, the second derivative of the free energy has the value,

<math> \chi_E^3 \biggl( \frac{n_e}{3B_e} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> -2 A\biggl( \frac{n_e}{3B_e} \biggr) + (1-\delta_{\infty n_c}) \biggl( \frac{n_e}{3B_e} \biggr) \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi_E^{1-3/n_c} + \delta_{\infty n_c} \biggl( \frac{n_e}{3B_e} \biggr) B_I \chi_E + \frac{3}{n_e}\biggl( \frac{n_e}{3B_e} \biggr) \biggl(1+\frac{3}{n_e}\biggr) B_e \chi_E^{1-3/n_e} </math>
	<math> = </math>	<math> -2 \alpha + (1-\delta_{\infty n_c}) \beta \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \delta_{\infty n_c} \beta_I \chi_E + \biggl(1+\frac{3}{n_e}\biggr) \chi_E^{1-3/n_e} \, , </math>

which, when combined with the condition for equilibrium gives,

<math> \chi_E^3 \biggl( \frac{n_e}{3B_e} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> -2 \alpha + (1-\delta_{\infty n_c}) \beta \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \delta_{\infty n_c} \beta_I \chi_E + \biggl(1+\frac{3}{n_e}\biggr) \biggl[ \alpha - (1-\delta_{\infty n_c}) \beta \chi_E^{1- 3/n_c} - \delta_{\infty n_c} \beta_I \chi_E \biggr] </math>
	<math> = </math>	<math> \alpha \biggl(\frac{3}{n_e}-1\biggr) + (1-\delta_{\infty n_c}) \beta \biggl(\frac{3}{n_c}-\frac{3}{n_e}\biggr) \chi_E^{1-3/n_c} - \delta_{\infty n_c} \beta_I \biggl(\frac{3}{n_e}\biggr)\chi_E </math>
<math> \Rightarrow ~~~~ \chi_E^3 \biggl( \frac{n_e^2}{3B_e} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> \alpha (3-n_e) - (1-\delta_{\infty n_c}) 3\beta \biggl(1 - \frac{n_e}{n_c} \biggr) \chi_E^{1-3/n_c} - \delta_{\infty n_c} 3\beta_I \chi_E \, . </math>

The equilibrium configuration is stable as long as this second derivative is positive.

Isothermal Core

Hence, for a bipolytrope with an isothermal core (<math>\delta_{\infty n_c} = 1</math>), the configuration is stable as long as,

<math> \chi_E < \frac{\alpha (3-n_e)}{3\beta_I} \, . </math>

Adiabatic Core

In the adiabatic case (<math>\delta_{\infty n_c} = 0</math>), the configuration is stable as long as,

<math> \chi_E^{1-3/n_c} < \frac{\alpha n_c (3-n_e)}{3\beta (n_c-n_e)} \, . </math>

Examples

Isothermal Core with <math>n_e=3/2</math>

Consider the case examined by Schönberg & Chandrasekhar (1942), that is, the case of an isothermal core and an envelope with <math>n_e = 3/2</math>. The equilibrium radius is given by the expression,

<math> \chi_E^{-1} </math>	<math>=</math>	<math> \alpha - \beta_I \chi_E \, </math>
<math> \Rightarrow ~~~~~ \beta_I \chi_E^{2} -\alpha \chi_E + 1 </math>	<math>=</math>	<math> 0 \, </math>
<math> \Rightarrow ~~~~~ \chi_E </math>	<math>=</math>	<math> \frac{1}{2\beta_I} \biggl[\alpha \pm \biggr(\alpha^2-4\beta_I \biggr)^{1/2}\biggr] \, </math>
	<math>=</math>	<math> \frac{\alpha}{2\beta_I} \biggl[1 \pm \biggr(1-\frac{4\beta_I}{\alpha^2} \biggr)^{1/2}\biggr] \, . </math>

And the system is stable when,

<math> \chi_E < \chi_0 \equiv \frac{\alpha }{2\beta_I} \, . </math>

A couple of physical attributes are now clear:

• Physical configurations only exist for <math>(4\beta_I/\alpha^2) \le 1</math>.
• For each value of <math>(4\beta_I/\alpha^2) < 1 \,</math>, there are two equilibrium configurations, given by the <math>\pm</math> roots of the quadratic equation for <math>\chi_E</math>; the "negative" branch is stable but the "positive" branch is unstable.

Note that,

<math> \chi_0 \equiv \frac{\alpha }{2\beta_I} = \biggl( \frac{GM_\mathrm{tot}}{10R_0 c_s^2} \biggr) \frac{\nu f(\nu,q)}{q} ~~~\Rightarrow ~~~ \biggl( \frac{10R_0 c_s^2}{GM_\mathrm{tot}} \biggr) = \frac{\nu f(\nu,q)}{q \chi_0} \, , </math>

and,

<math> \frac{4\beta_I}{\alpha^2 } = \biggl( \frac{10 R_0 c_s^2 }{GM_\mathrm{tot}} \biggr)^2 \biggl[ \frac{K_e (\rho_e|_0)^{1/n_e}}{c_s^2} \biggr] \frac{q^2(1-\nu)}{\nu^3 f^2(\nu,q)} = \biggl[ \frac{K_e (\rho_e|_0)^{1/n_e}}{c_s^2} \biggr] \frac{q^2(1-\nu)}{\nu^3 f^2(\nu,q)} \biggl[\frac{\nu f(\nu,q)}{q \chi_0} \biggr]^2 = \biggl[ \frac{\mu_c}{\mu_e} \biggr] \biggl( \frac{1}{\nu} - 1 \biggr) \, . </math>

But, this last expression must be less than or equal to unity, which implies,

<math> \frac{1}{\nu} \le 1 + \frac{\mu_e}{\mu_c} ~~~\Rightarrow ~~~ \nu \ge \biggl(1 + \frac{\mu_e}{\mu_c} \biggr)^{-1} </math> This doesn't seem to have the correct behavior, for example, the smaller values of <math>\nu</math> should be the stable ones, so there must be a mistake in the derivation.

Adiabatic Core with <math>n_c = 5</math> and <math>n_e=1</math>

Consider the case with an analytical structure derived by Eagleton, Faulkner, and Cannon (1998, MNRAS, 298, 831), that is, the case of an adiabatic core having <math>n_c=5</math> and an envelope with <math>n_e = 1</math>. The equilibrium radius is,

Old and Probably Irrelevant Discussion

Summary Expressions (New)

In the above derivations, we have adopted the notation,

<math> \rho_\mathrm{norm} \equiv \frac{3M_\mathrm{tot}}{4\pi R_0^3} \, . </math>

Now, guided by the earlier discussion of pressure-bounded isothermal spheres, we choose the following normalization energy and radius:

<math> E_0 = 3M_\mathrm{tot} c_s^2 </math>         and         <math> R_0 = \frac{GM_\mathrm{tot}}{5c_s^2} \, . </math>

Also, by analogy, it is useful to define the dimensionless parameter,

<math> \Pi_I \equiv \frac{K_e \rho_\mathrm{norm}^{1/n_e}}{c_s^2} = \frac{K_e}{c_s^2} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr]^{1/n_e} = \biggl( \frac{3\cdot 5^3}{4\pi} \biggr)^{1/n_e} \frac{K_e}{c_s^2} \biggl[ \frac{c_s^6}{G^3 M_\mathrm{tot}^2} \biggr]^{1/n_e} \, . </math>

(It is worth noting that if we set <math>n_e = -1</math>, the dimensionless parameter <math>\Pi_I</math> becomes identical to the parameter <math>\Pi</math> as defined in the context of our discussion of the Bonnor-Ebert sphere. But in order to complete the analogy with the Bonnor-Ebert sphere discussion, we would also need to change the sign on the last term in the above expression for the free energy because in the earlier discussion the external pressure was an external, confining condition whereas here it is included as an internal energy of the system.)

Relevant Expressions for Isothermal Core
<math> \frac{\rho_e}{\rho_c}= \frac{\mu_e}{\mu_c} </math>	<math> \frac{q^3}{\nu}\biggl( \frac{1 - \nu}{1- q^3} \biggr) </math>
<math> \chi \equiv \frac{R}{R_0} </math>	<math> \Pi_I^{n_e/3} [\nu^{-n_e}\ (1-\nu)^{n_e+1} ]^{1/3} q^{n_e} (1-q^3)^{-(n_e+1)/3} </math>
<math> \chi^3 = \biggl(\frac{R}{R_0} \biggr)^{3} </math>	<math> \Pi_I^{n_e} \biggl( \frac{\rho_e}{\rho_c}\biggr)^{n_e + 1} \biggl[ q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)(1-q^3) \biggr]^{-1} </math>
<math> \frac{A}{E_0} </math>	<math> \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} </math>	<math>= \biggl( \frac{\nu^2}{q} \biggr) \biggl\{ f_A(\nu,q) \biggr\}</math>
<math> \frac{B_e}{E_0} </math>	<math> \Pi_I \biggl( \frac{n_e}{3} \biggr) (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} </math>
<math> \frac{B_I}{E_0} </math>	<math>\nu </math>
<math> \frac{\mathfrak{G}}{E_0} </math>	<math> - \frac{A}{E_0} \chi^{-1} - \frac{B_I}{E_0} \ln\chi + \frac{B_e}{E_0} \chi^{-3/n_e} </math>	<math> = \nu \biggl[ - \biggl( \frac{\nu}{q} \biggr) \frac{f_A(\nu,q)}{\chi} - \ln\chi + \frac{n_e}{3} \biggl(\frac{1}{q^3}-1\biggr)\biggr] </math>

[On 8 November 2013, J. E. Tohline wrote: I just confirmed that the simpler expression for the normalized total free energy, <math>\mathfrak{G}/E_0</math>, matches the more complicated version. I don't like the result because the third term in the free energy -- the one contributed by the internal energy of the envelope -- is independent of the radius of the configuration, <math>\chi</math>; it works out this way because my expression for <math>\Pi_I</math> has a radial dependence that exactly cancels out the explicit radial dependence that appears in the more complicated expression. But maybe it's okay after all because this expression is intended to show how the free energy varies across the <math>(q,\nu)</math> plane, and the effect of <math>\Pi_I</math> appears implicitly through the specification of <math>\chi</math>, or visa versa.]

Summary Expressions (Old)

In the above derivations, we have adopted the notation,

<math> \rho_\mathrm{norm} \equiv \frac{3M_\mathrm{tot}}{4\pi R_0^3} \, . </math>

Now, guided by the dimensional aspects of the various coefficients in the free energy expression, we choose the following normalization energy and radius:

<math> E_0 = M_\mathrm{tot} K_e \rho_\mathrm{norm}^{1/n_e} </math>         and         <math> R_0 = \frac{GM_\mathrm{tot}}{K_e \rho_\mathrm{norm}^{1/n_e}} \, . </math>

When combined with the expression for <math>\rho_\mathrm{norm}</math>, these become,

<math> E_0 = \biggl[ \biggl( \frac{4\pi}{3} \biggr) G^3 M_\mathrm{tot}^{5-n_e} K_e^{-n_e}\biggr]^{1/(3-n_e)} </math>         and         <math> R_0 = \biggl[ \frac{3M_\mathrm{tot}}{4\pi} \biggl( \frac{K_e}{GM_\mathrm{tot}} \biggr)^{n_e} \biggr]^{1/(3-n_e)} \, . </math>

So, the primary scales are determined after specifying two parameters: <math>M_\mathrm{tot}</math> and <math>K_e</math>. We also obtain,

<math> \kappa_I \equiv \frac{c_s^2}{K_e \rho_\mathrm{norm}^{1/n_e}} = \frac{M_\mathrm{tot} c_s^2}{E_0} = c_s^2 \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{K_e^{n_e}}{G^3 M_\mathrm{tot}^2} \biggr]^{1/(3-n_e)} \, . </math>

Relevant Expressions for Isothermal Core
<math> \frac{\rho_e}{\rho_c} </math>	<math> \frac{q^3}{\nu}\biggl( \frac{1 - \nu}{1- q^3} \biggr) </math>
<math> \chi \equiv \frac{R}{R_0} </math>	<math> q^{n_e} (1-q^3)^{-(n_e+1)/3} \biggl[\nu^{-n_e}\ (1-\nu)^{n_e+1} \kappa_I^{-n_e} \biggr]^{1/3} </math>
<math> \frac{A}{E_0} </math>	<math> \biggl( \frac{3}{5} \biggr)\nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} </math>
<math> \frac{B_e}{E_0} </math>	<math> n_e(1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} </math>
<math> \frac{B_I}{E_0} </math>	<math> 3 \kappa_I \nu </math>
<math> \frac{\mathfrak{G}}{E_0} </math>	<math> - \frac{A}{E_0} \chi^{-1} - \frac{B_I}{E_0} \ln\chi + \frac{B_e}{E_0} \chi^{-3/n_e} </math>

Subsequently, we will also find it useful to have expressions for the following coefficient ratios:

<math>\frac{n_e A}{3 B_e}</math>	<math>=</math>	<math> \biggl( \frac{GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ f(\rho_e/\rho_c , \xi_s) \biggr\} \biggl[K_e M_\mathrm{tot} \rho_\mathrm{norm}^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e}\biggr]^{-1} </math>
	<math>=</math>	<math> \biggl( \frac{GM_\mathrm{tot}}{5K_e \rho_\mathrm{norm}^{1/n_e} R_0} \biggr) \nu^2 \xi_s \biggl\{ f(\rho_e/\rho_c , \xi_s) \biggr\} (1 - \nu)^{-(1+1/n_e)} q^{3/n_e} \biggl(\frac{1}{q^3} - 1 \biggr)^{1/n_e} </math>
	<math>=</math>	<math> \biggl( \frac{GM_\mathrm{tot}}{5K_e \rho_\mathrm{norm}^{1/n_e} R_0} \biggr) \nu^2 q^{-1} [ (1 - \nu)^{-(n_e+1)} (1 - q^3 ) ]^{1/n_e} \biggl\{ f(\rho_e/\rho_c , \xi_s) \biggr\} \, ; </math>

<math>\frac{n_e B_I}{3 B_e}</math>	<math>=</math>	<math> M_\mathrm{tot} c_s^2 \nu \biggl[K_e M_\mathrm{tot} \rho_\mathrm{norm}^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e}\biggr]^{-1} </math>
	<math>=</math>	<math> \kappa_I \nu (1 - \nu)^{-(1+1/n_e)} q^{3/n_e} \biggl(\frac{1}{q^3} - 1 \biggr)^{1/n_e} </math>
	<math>=</math>	<math> \kappa_I \nu \biggl[ (1 - \nu)^{-(n_e+1)} (1-q^{3}) \biggr]^{1/n_e} \, ; </math>

<math>\frac{n_e B_c}{n_c B_e}</math>	<math>=</math>	<math> \biggl[K_c M_\mathrm{tot} \rho_\mathrm{norm}^{1/n_c} \nu^{1+1/n_c}\xi_s^{3/n_c} \biggr] \biggl[K_e M_\mathrm{tot} \rho_\mathrm{norm}^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e}\biggr]^{-1} </math>
	<math>=</math>	<math> \kappa_A \nu^{1+1/n_c}\xi_s^{3/n_c} \biggl[ (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e}\biggr]^{-1} </math>
	<math>=</math>	<math> \kappa_A \biggl[\nu^{1+1/n_c} (1 - \nu)^{-(1+1/n_e)} \biggr] \biggl[ \xi_s^{3(1/n_c-1/n_e)} (\xi_s^3 - 1)^{1/n_e}\biggr] </math>
	<math>=</math>	<math> \kappa_A \biggl[\nu^{1+1/n_c} (1 - \nu)^{-(1+1/n_e)} \biggr] \biggl[ q^{3(1/n_e-1/n_c)} \biggl( \frac{1}{q^3} - 1\biggr)^{1/n_e}\biggr] </math>
	<math>=</math>	<math> \kappa_A \biggl[\nu^{1+1/n_c} (1 - \nu)^{-(1+1/n_e)} \biggr] \biggl[ q^{-3n_e/n_c} (1-q^3) \biggr]^{1/n_e} </math>
	<math>=</math>	<math> \kappa_A \biggl[\nu^{1+1/n_c} q^{-3/n_c} \biggr] \biggl[ (1 - \nu)^{-(n_e+1)} (1-q^3) \biggr]^{1/n_e} \, . </math>

Derivatives of Free Energy

<math> \frac{\partial\mathfrak{G}}{\partial \chi} = A \chi^{-2} -(1-\delta_{\infty n_c}) \frac{3}{n_c} B_c \chi^{-(1+3/n_c)} - \delta_{\infty n_c} B_I \chi^{-1} -\frac{3}{n_e} B_e \chi^{-(1+3/n_e)} \, ; </math>

<math> \frac{\partial^2\mathfrak{G}}{\partial \chi^2} = -2 A \chi^{-3} + (1-\delta_{\infty n_c}) \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi^{-(2+3/n_c)} + \delta_{\infty n_c} B_I \chi^{-2} + \frac{3}{n_e} \biggl(1+\frac{3}{n_e}\biggr) B_e \chi^{-(2+3/n_e)} \, . </math>

Equilibrium Condition

We obtain the equilibrium radius, <math>\chi_E</math>, when <math>\partial\mathfrak{G}/\partial\chi = 0</math>. Hence, the relation governing the equilibrium radius is,

<math> A \chi_E^{-2} </math>	<math>=</math>	<math> (1-\delta_{\infty n_c}) \frac{3}{n_c} B_c \chi_E^{-1- 3/n_c)} +\delta_{\infty n_c} B_I \chi_E^{-1} +\frac{3}{n_e} B_e \chi_E^{-1-3/n_e)} </math>
<math> \Rightarrow ~~~~~ \frac{n_e A}{3B_e} </math>	<math>=</math>	<math> (1-\delta_{\infty n_c}) \frac{n_e B_c}{n_c B_e} \chi_E^{1- 3/n_c} +\delta_{\infty n_c} \frac{n_e B_I}{3B_e} \chi_E + \chi_E^{1-3/n_e} </math>
<math> \Rightarrow ~~~~~ \chi_E^{1-3/n_e} </math>	<math>=</math>	<math> \alpha - (1-\delta_{\infty n_c}) \beta \chi_E^{1- 3/n_c} - \delta_{\infty n_c} \beta_I \chi_E \, , </math>

where,

<math>\alpha \equiv \frac{n_e A}{3B_e} \, ; ~~~ \beta \equiv \frac{n_e B_c}{n_c B_e} \, ; ~~~ \beta_I \equiv \frac{n_e B_I}{3B_e} \, .</math>

Stability

At this equilibrium radius, the second derivative of the free energy has the value,

<math> \chi_E^3 \biggl( \frac{n_e}{3B_e} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> -2 A\biggl( \frac{n_e}{3B_e} \biggr) + (1-\delta_{\infty n_c}) \biggl( \frac{n_e}{3B_e} \biggr) \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi_E^{1-3/n_c} + \delta_{\infty n_c} \biggl( \frac{n_e}{3B_e} \biggr) B_I \chi_E + \frac{3}{n_e}\biggl( \frac{n_e}{3B_e} \biggr) \biggl(1+\frac{3}{n_e}\biggr) B_e \chi_E^{1-3/n_e} </math>
	<math> = </math>	<math> -2 \alpha + (1-\delta_{\infty n_c}) \beta \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \delta_{\infty n_c} \beta_I \chi_E + \biggl(1+\frac{3}{n_e}\biggr) \chi_E^{1-3/n_e} \, , </math>

which, when combined with the condition for equilibrium gives,

<math> \chi_E^3 \biggl( \frac{n_e}{3B_e} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> -2 \alpha + (1-\delta_{\infty n_c}) \beta \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \delta_{\infty n_c} \beta_I \chi_E + \biggl(1+\frac{3}{n_e}\biggr) \biggl[ \alpha - (1-\delta_{\infty n_c}) \beta \chi_E^{1- 3/n_c} - \delta_{\infty n_c} \beta_I \chi_E \biggr] </math>
	<math> = </math>	<math> \alpha \biggl(\frac{3}{n_e}-1\biggr) + (1-\delta_{\infty n_c}) \beta \biggl(\frac{3}{n_c}-\frac{3}{n_e}\biggr) \chi_E^{1-3/n_c} - \delta_{\infty n_c} \beta_I \biggl(\frac{3}{n_e}\biggr)\chi_E </math>
<math> \Rightarrow ~~~~ \chi_E^3 \biggl( \frac{n_e^2}{3B_e} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> \alpha (3-n_e) - (1-\delta_{\infty n_c}) 3\beta \biggl(1 - \frac{n_e}{n_c} \biggr) \chi_E^{1-3/n_c} - \delta_{\infty n_c} 3\beta_I \chi_E \, . </math>

Finally, the equilibrium configuration is stable as long as this second derivative is positive. Hence, for a bipolytrope with an isothermal core (<math>\delta_{\infty n_c} = 1</math>), the configuration is stable as long as,

<math> \chi_E < \frac{\alpha (3-n_e)}{3\beta_I} \, . </math>

In the adiabatic case (<math>\delta_{\infty n_c} = 0</math>), the configuration is stable as long as,

<math> \chi_E^{1-3/n_c} < \frac{\alpha n_c (3-n_e)}{3\beta (n_c-n_e)} \, . </math>

Examples

Isothermal Core with <math>n=3/2</math> Envelope

When the core is isothermal and <math>n_e = 3/2</math>, the equilibrium condition is:

<math> \chi_E^{-1} = \alpha - \beta_I \chi_E \, , </math>

<math> \Rightarrow ~~~~ \beta_I \chi_E^2 - \alpha \chi_E + 1 = 0 \, , </math>

<math> \Rightarrow ~~~~ \chi_E = \frac{1}{2\beta_I} \biggl[ \alpha \pm \sqrt{\alpha^2 - 4\beta_I} \biggr] = \frac{\alpha}{2\beta_I} \biggl[ 1 \pm \sqrt{1 - \frac{4\beta_I}{\alpha^2}} \biggr] \, . </math>

At the same time, the condition for stability is,

<math> \chi_E < \frac{\alpha}{2\beta_I} \, . </math>

Isothermal Core with <math>n=1</math> Envelope

When the core is isothermal and <math>n_e = 1</math>, the equilibrium condition is:

<math> \chi_E^{-2} = \alpha - \beta_I \chi_E \, , </math>

<math> \Rightarrow ~~~~ \chi_E^3 - \frac{\alpha}{\beta_I} \chi_E^2 + \frac{1}{\beta_I} = 0 \, . </math>

(We need to solve this cubic equation.)

At the same time, the condition for stability is,

<math> \chi_E < \frac{2\alpha}{3\beta_I} \, . </math>

Old (and probably incorrect) cases

Envelope with <math>n=3/2</math>

If we choose an <math>n_e = 3/2</math> envelope, we obtain stability for,

<math> \chi_E < \frac{2\beta}{\alpha}\, . </math>

In this case, the equilibrium radius condition is,

<math> \chi_E^2 - \alpha \chi_E + \beta =0 </math>

<math> \Rightarrow ~~~~ \chi_E = \frac{1}{2}\biggl[\alpha \pm \biggl( \alpha^2 -4\beta \biggr)^{1/2} \biggr] = \frac{\alpha}{2}\biggl[1 \pm \biggl( 1 -\frac{4\beta}{\alpha^2} \biggr)^{1/2} \biggr] </math>

Envelope with <math>n=1</math>

If, instead, we choose an <math>n_e = 1</math> envelope, we obtain stability for,

<math> \chi_E < \sqrt{\frac{3\beta}{\alpha} }\, . </math>

In this case, the equilibrium radius condition is,

<math> \alpha = \chi_E + \beta \chi_E^{-2} \, , </math>

<math> \Rightarrow ~~~~ \chi_E^3 - \alpha \chi_E^2 + \beta = 0 \, . </math>

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation