Difference between revisions of "User:Tohline/SSC/Structure/BiPolytropes/Analytic5 1"
(→Parameter Values: Add some text) |
(→Parameter Values: Insert text describing plots in Figure 1) |
||
| Line 425: | Line 425: | ||
==Parameter Values== | ==Parameter Values== | ||
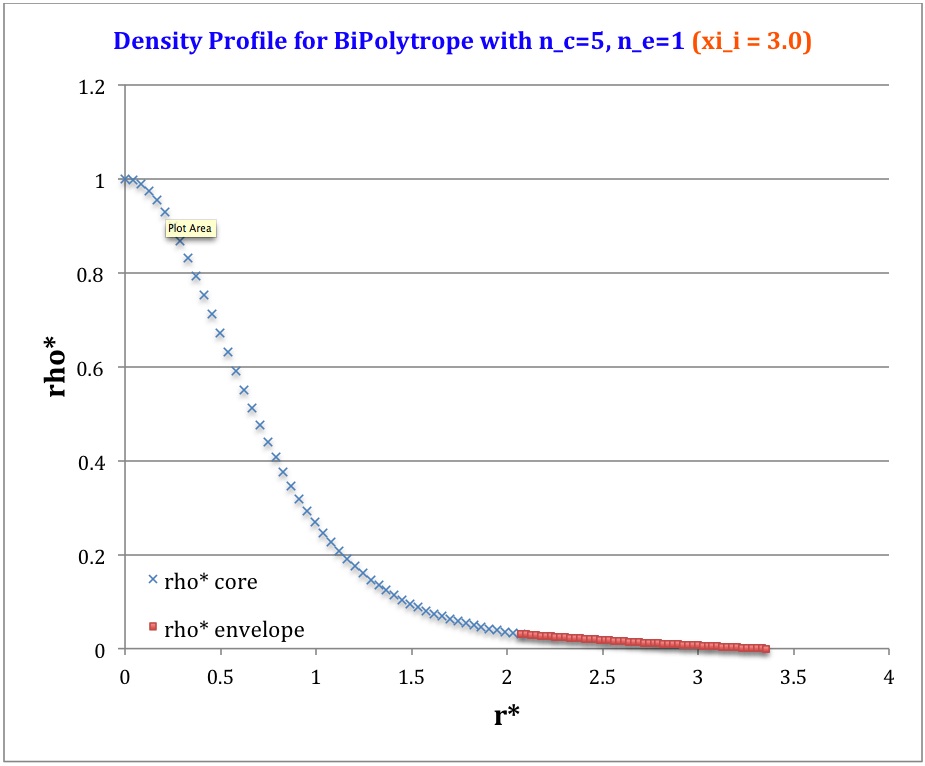
The <math>2^\mathrm{nd}</math> column of Table 1 catalogues the analytic expressions that define various parameters and physical properties (as identified, respectively, in column 1) of the <math>n_c=5</math>, <math>n_e=1</math> bipolytrope. We have evaluated these expressions for various choices of the dimensionless interface | The <math>2^\mathrm{nd}</math> column of Table 1 catalogues the analytic expressions that define various parameters and physical properties (as identified, respectively, in column 1) of the <math>n_c=5</math>, <math>n_e=1</math> bipolytrope. We have evaluated these expressions for various choices of the dimensionless interface radius, <math>\xi_i</math>, and have tabulated the results in the last few columns of the table. The tabulated values have been derived assuming <math>\mu_e/\mu_c = 1</math>, that is, assuming that the core and the envelope have the same mean molecular weights. The tabulated values of various parameters can be adjusted to correspond to other choices of this ratio by multiplying by the appropriate scaling coefficient as shown in column 1 of Table 1. For example, if the interface is positioned at <math>\xi_i = 0.5</math> but <math>\mu_e/\mu_c = 0.2</math>, then <math>\eta_i= 4.0</math> instead of <math>0.8</math>. | ||
<!-- BEGIN TABLE OF PARAMETERS ---> | <!-- BEGIN TABLE OF PARAMETERS ---> | ||
| Line 852: | Line 852: | ||
</div> | </div> | ||
<!-- END TABLE OF PARAMETERS ---> | <!-- END TABLE OF PARAMETERS ---> | ||
For a given choice of <math>\mu_e/\mu_c</math> a physically relevant sequence of models can be constructed by steadily increasing the value of <math>\xi_i</math> from zero to infinity — or at least to some value, <math>\xi_i \gg 1</math>. The blue curve shown on the left-hand side of Figure 1 presents one such model sequence, generated for the choice <math>\mu_e/\mu_c = 0.2</math>. The curve shows how the fractional core mass, <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>, varies in relation to the fractional core radius, <math>q \equiv r^*_\mathrm{core}/R^*_\mathrm{tot}</math>; the analytic expressions for these two ratios are presented in the last two rows of Table 1. | |||
The expectation is that an increase in <math>\xi_i</math> along the sequence will correspond to an increase in the size — both the radius and the mass — of the core. This expectation is realized | |||
<div align="center"> | <div align="center"> | ||
<table border="1" cellpadding="5" width="80%"> | <table border="1" cellpadding="5" width="80%"> | ||
<tr> | |||
<td align="center" colspan="2"> | |||
<b> | |||
Figure 1: Fractional mass versus fractional radius along the equilibrium sequence | |||
</b> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
Revision as of 22:27, 18 April 2013
BiPolytrope with <math>n_c = 5</math> and <math>n_e=1</math>

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Here we construct a bipolytrope in which the core has an <math>n_c=5</math> polytropic index and the envelope has an <math>n_c=1</math> polytropic index. This system is particularly interesting because the entire structure can be described by closed-form, analytic expressions. As far as I have been able to determine, this analytic structural model has not previously been published in a refereed, archival journal (author: Joel E. Tohline, March 30, 2013). In deriving the properties of this model, we will follow the general solution steps for constructing a bipolytrope that we have outlined elsewhere.
Steps 2 & 3
Based on the discussion presented elsewhere of the structure of an isolated <math>n=5</math> polytrope, the core of this bipolytrope will have the following properties:
<math> \theta(\xi) = \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-1/2} ~~~~\Rightarrow ~~~~ \theta_i = \biggl[ 1 + \frac{1}{3}\xi_i^2 \biggr]^{-1/2} ; </math>
<math> \frac{d\theta}{d\xi} = - \frac{\xi}{3}\biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3/2} ~~~~\Rightarrow ~~~~ \biggl(\frac{d\theta}{d\xi}\biggr)_i = - \frac{\xi_i}{3}\biggl[ 1 + \frac{1}{3}\xi_i^2 \biggr]^{-3/2} \, . </math>
The first zero of the function <math>\theta(\xi)</math> and, hence, the surface of the corresponding isolated <math>n=5</math> polytrope is located at <math>\xi_s = \infty</math>. Hence, the interface between the core and the envelope can be positioned anywhere within the range, <math>0 < \xi_i < \infty</math>.
Step 4: Throughout the core (<math>0 \le \xi \le \xi_i</math>)
|
Specify: <math>K_c</math> and <math>\rho_0 ~\Rightarrow</math> |
|
|||
|
<math>\rho</math> |
<math>=</math> |
<math>\rho_0 \theta^{n_c}</math> |
<math>=</math> |
<math>\rho_0 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2}</math> |
|
<math>P</math> |
<math>=</math> |
<math>K_c \rho_0^{1+1/n_c} \theta^{n_c + 1}</math> |
<math>=</math> |
<math>K_c \rho_0^{6/5} \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3}</math> |
|
<math>r</math> |
<math>=</math> |
<math>\biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{1/2} \rho_0^{(1-n_c)/(2n_c)} \xi</math> |
<math>=</math> |
<math>\biggl[ \frac{K_c}{G\rho_0^{4/5}} \biggr]^{1/2} \biggl(\frac{3}{2\pi}\biggr)^{1/2} \xi</math> |
|
<math>M_r</math> |
<math>=</math> |
<math>4\pi \biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{3/2} \rho_0^{(3-n_c)/(2n_c)} \biggl(-\xi^2 \frac{d\theta}{d\xi} \biggr)</math> |
<math>=</math> |
<math>\biggl[ \frac{K_c^3}{G^3 \rho_0^{2/5} } \biggr]^{1/2} \biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]</math> |
Step 5: Interface Conditions
|
|
Setting <math>n_c=5</math>, <math>n_e=1</math>, and <math>\phi_i = 1 ~~~~\Rightarrow</math> |
|||
|
<math>\frac{\rho_e}{\rho_0}</math> |
<math>=</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{n_c}_i \phi_i^{-n_e}</math> |
<math>=</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i </math> |
|
<math>\biggl( \frac{K_e}{K_c} \biggr) </math> |
<math>=</math> |
<math>\rho_0^{1/n_c - 1/n_e}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-(1+1/n_e)} \theta^{1 - n_c/n_e}_i</math> |
<math>=</math> |
<math>\rho_0^{-4/5}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-4}_i</math> |
|
<math>\frac{\eta_i}{\xi_i}</math> |
<math>=</math> |
<math>\biggl[ \frac{n_c + 1}{n_e+1} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{(n_c-1)/2} \phi_i^{(1-n_e)/2}</math> |
<math>=</math> |
<math>3^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{2}</math> |
|
<math>\biggl( \frac{d\phi}{d\eta} \biggr)_i</math> |
<math>=</math> |
<math>\biggl[ \frac{n_c + 1}{n_e + 1} \biggr]^{1/2} \theta_i^{- (n_c + 1)/2} \phi_i^{(n_e+1)/2} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math> |
<math>=</math> |
<math>3^{1/2} \theta_i^{- 3} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math> |
Step 6: Envelope Solution
Adopting equation (8) of Beech (1988), the most general solution to the <math>n=1</math> Lane-Emden equation can be written in the form,
<math> \phi = A \biggl[ \frac{\sin(\eta - B)}{\eta} \biggr] \, , </math>
where <math>A</math> and <math>B</math> are constants. The first derivative of this function is,
<math> \frac{d\phi}{d\eta} = \frac{A}{\eta^2} \biggl[ \eta\cos(\eta-B) - \sin(\eta-B) \biggr] \, . </math>
From Step 5, above, we know the value of the function, <math>\phi</math> and its first derivative at the interface; specifically,
<math> \phi_i = 1~~~~\mathrm{and} ~~~~\biggl( \frac{d\phi}{d\eta}\biggr)_i =3^{1/2} \theta_i^{- 3} \biggl( \frac{d\theta}{d\xi} \biggr)_i~~~~ \mathrm{at}~~~~\eta_i =3^{1/2} \xi_i \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{2}</math>
From this information we can determine the constants <math>A</math> and <math>B</math>; specifically,
<math> \eta_i - B = \tan^{-1}(\Lambda_i^{-1}) = \frac{\pi}{2}- \tan^{-1}(\Lambda_i) \, , </math>
<math> A = \frac{\phi_i \eta_i}{\sin(\eta_i - B)} = \phi_i \eta_i (1 + \Lambda_i^2)^{1/2} \, , </math>
where,
<math> \Lambda_i = \frac{1}{\eta_i} + \frac{1}{\phi_i} \biggl(\frac{d\phi}{d\eta}\biggr)_i \, . </math>
Step 7
The surface will be defined by the location, <math>\eta_s</math>, at which the function <math>\phi(\eta)</math> first goes to zero, that is,
<math> \eta_s = \pi + B = \frac{\pi}{2} + \eta_i + \tan^{-1}(\Lambda_i) \, . </math>
Step 8: Throughout the envelope (<math>\eta_i \le \eta \le \eta_s</math>)
|
|
Knowing: <math>K_e/K_c</math> and <math>\rho_e/\rho_0</math> from Step 5 <math>\Rightarrow</math> |
|||||
|
<math>\rho</math> |
<math>=</math> |
<math>\rho_e \phi^{n_e}</math> |
<math>=</math> |
<math>\rho_0 \biggl(\frac{\rho_e}{\rho_0}\biggr) \phi</math> |
<math>=</math> |
<math>\rho_0 \biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i \phi</math> |
|
<math>P</math> |
<math>=</math> |
<math>K_e \rho_e^{1+1/n_e} \phi^{n_e + 1}</math> |
<math>=</math> |
<math>K_c \rho_0^{6/5} \biggl(\frac{K_e \rho_0^{4/5}}{K_c}\biggr) \biggl(\frac{\rho_e}{\rho_0}\biggr)^{2} \phi^{2}</math> |
<math>=</math> |
<math>K_c \rho_0^{6/5} \theta^{6}_i \phi^{2}</math> |
|
<math>r</math> |
<math>=</math> |
<math>\biggl[ \frac{(n_e + 1)K_e}{4\pi G} \biggr]^{1/2} \rho_e^{(1-n_e)/(2n_e)} \eta</math> |
<math>=</math> |
<math>\biggl[ \frac{K_c}{G \rho_0^{4/5}} \biggr]^{1/2} \biggl( \frac{K_e \rho_0^{4/5}}{K_c} \biggr)^{1/2} (2\pi)^{-1/2}\eta</math> |
<math>=</math> |
<math>\biggl[ \frac{K_c}{G \rho_0^{4/5}} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta</math> |
|
<math>M_r</math> |
<math>=</math> |
<math>4\pi \biggl[ \frac{(n_e + 1)K_e}{4\pi G} \biggr]^{3/2} \rho_e^{(3-n_e)/(2n_e)} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
<math>=</math> |
<math>\biggl[ \frac{K_c^3}{G^3 \rho_0^{2/5}} \biggr]^{1/2} \biggl( \frac{K_e \rho_0^{4/5}}{K_c} \biggr)^{3/2} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
<math>=</math> |
<math>\biggl[ \frac{K_c^3}{G^3 \rho_0^{2/5}} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
Examples
Normalization
The dimensionless variables used in Tables 1 & 2 are defined as follows:
|
<math>\rho^*</math> |
<math>\equiv</math> |
<math>\frac{\rho}{\rho_0}</math> |
; |
<math>r^*</math> |
<math>\equiv</math> |
<math>\frac{r}{[K_c^{1/2}/(G^{1/2}\rho_0^{2/5})]}</math> |
|
<math>P^*</math> |
<math>\equiv</math> |
<math>\frac{P}{K_c\rho_0^{6/5}}</math> |
; |
<math>M_r^*</math> |
<math>\equiv</math> |
<math>\frac{M_r}{[K_c^{3/2}/(G^{3/2}\rho_0^{1/5})]}</math> |
|
<math>H^*</math> |
<math>\equiv</math> |
<math>\frac{H}{K_c\rho_0^{1/5}}</math> |
. |
|
||
Parameter Values
The <math>2^\mathrm{nd}</math> column of Table 1 catalogues the analytic expressions that define various parameters and physical properties (as identified, respectively, in column 1) of the <math>n_c=5</math>, <math>n_e=1</math> bipolytrope. We have evaluated these expressions for various choices of the dimensionless interface radius, <math>\xi_i</math>, and have tabulated the results in the last few columns of the table. The tabulated values have been derived assuming <math>\mu_e/\mu_c = 1</math>, that is, assuming that the core and the envelope have the same mean molecular weights. The tabulated values of various parameters can be adjusted to correspond to other choices of this ratio by multiplying by the appropriate scaling coefficient as shown in column 1 of Table 1. For example, if the interface is positioned at <math>\xi_i = 0.5</math> but <math>\mu_e/\mu_c = 0.2</math>, then <math>\eta_i= 4.0</math> instead of <math>0.8</math>.
Table 1: Properties of <math>n_c=5</math>, <math>n_e=1</math>, BiPolytrope Having Various Interface Locations, <math>\xi_i</math>
File:BiPolytropeParametersV01.xml
|
Parameter |
<math>\xi_i</math> |
0.5 |
1.0 |
3.0 |
10 |
|
<math>\theta_i</math> |
<math>\biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-1/2}</math> |
0.96077 |
0.86603 |
0.50000 |
|
|
<math>-\biggl(\frac{d\theta_i}{d\xi}\biggr)_i</math> |
<math>\frac{1}{3} \xi_i \biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-3/2}</math> |
0.14781 |
0.21651 |
0.12500 |
|
|
<math>r^*_\mathrm{core} \equiv r^*_i</math> |
<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi_i</math> |
0.34549 |
0.69099 |
2.07297 |
|
|
<math>\rho^*_i \biggr|_c = \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \rho^*_i \biggr|_e</math> |
<math>\biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-5/2}</math> |
0.81864 |
0.48714 |
0.03125 |
|
|
<math>P^*_i</math> |
<math>\biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-3}</math> |
0.78653 |
0.42188 |
0.01563 |
|
|
<math>H^*_i \biggr|_c = \frac{n_c+1}{n_e+1} \biggl( \frac{\mu_e}{\mu_c} \biggr) H^*_i \biggr|_e</math> |
<math>6 \biggl( 1+\frac{1}{3}\xi_i^2 \biggr)^{-1/2}</math> |
5.76461 |
5.19615 |
3.00000 |
|
|
<math>M^*_\mathrm{core}</math> |
<math>\biggl( \frac{6}{\pi}\biggr)^{1/2} (\xi_i \theta_i)^3</math> |
0.15320 |
0.89762 |
4.66417 |
|
|
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1}\eta_i</math> |
<math>\sqrt{3} ~\theta_i^2 \xi_i</math> |
0.79941 |
1.29904 |
1.29904 |
|
|
<math>-\biggl( \frac{d\phi}{d\eta} \biggr)_i</math> |
<math>\sqrt{3} ~\theta_i^{-3} \biggl( - \frac{d\theta}{d\xi} \biggr)_i = \frac{\xi_i}{\sqrt{3}}</math> |
0.28868 |
0.57735 |
1.73205 |
|
|
<math>\Lambda_i</math> |
<math>\frac{1}{\eta_i} + \biggl( \frac{d\phi}{d\eta} \biggr)_i</math> |
0.96225 |
0.19245 |
-0.96225 |
|
|
<math>A</math> |
<math>\eta_i (1 + \Lambda_i^2)^{1/2}</math> |
1.10940 |
1.32288 |
1.80278 |
|
|
<math>B</math> |
<math>\eta_i - \frac{\pi}{2} + \tan^{-1}( \Lambda_i)</math> |
- 0.00523 |
-0.08163 |
-1.03792 |
|
|
<math>\eta_s</math> |
<math>\pi + B</math> |
3.13637 |
3.05996 |
2.10367 |
|
|
<math>- \biggl( \frac{d\phi}{d\eta} \biggr)_s</math> |
<math>\frac{A}{\eta_s}</math> |
0.35372 |
0.43232 |
0.85697 |
|
|
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \cdot \biggl[ R^* \equiv r^*_s \biggr]</math> |
<math>\frac{\eta_s}{\sqrt{2\pi} ~\theta_i^2}</math> |
1.35550 |
1.62766 |
3.35697 |
|
|
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^2 M^*_\mathrm{tot}</math> |
<math>\biggl(\frac{2}{\pi}\biggr)^{1/2} \theta_i^{-1} \biggl( -\eta^2 \frac{d\phi}{d\eta} \biggr)_s = \biggl(\frac{2}{\pi}\biggr)^{1/2} \frac{A\eta_s}{\theta_i}</math> |
2.88959 |
3.72945 |
6.05187 |
|
|
<math>\biggl(\frac{\mu_e}{\mu_c}\biggr)^{-2} \cdot \biggl[ \nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} \biggr]</math> |
<math>\sqrt{3} ~\biggl( \frac{\xi_i^3 \theta_i^4}{A\eta_s} \biggr)</math> |
0.05302 |
0.24068 |
0.77070 |
|
|
<math>\biggl(\frac{\mu_e}{\mu_c}\biggr)^{-1} \cdot \biggl[ q \equiv \frac{r_\mathrm{core}}{R} \biggr]</math> |
<math>\sqrt{3}~\biggl[\frac{\xi_i \theta_i^2}{\eta_s}\biggr]</math> |
0.25488 |
0.42453 |
0.61751 |
|
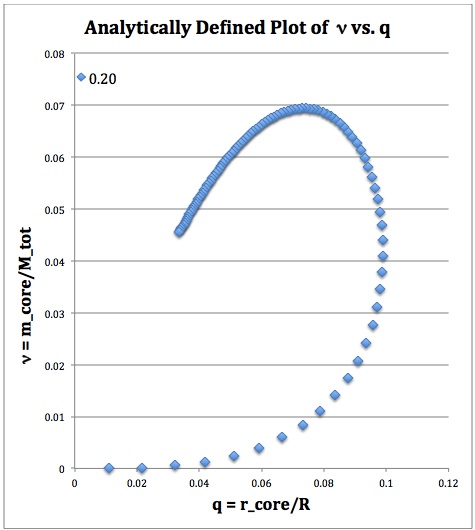
For a given choice of <math>\mu_e/\mu_c</math> a physically relevant sequence of models can be constructed by steadily increasing the value of <math>\xi_i</math> from zero to infinity — or at least to some value, <math>\xi_i \gg 1</math>. The blue curve shown on the left-hand side of Figure 1 presents one such model sequence, generated for the choice <math>\mu_e/\mu_c = 0.2</math>. The curve shows how the fractional core mass, <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>, varies in relation to the fractional core radius, <math>q \equiv r^*_\mathrm{core}/R^*_\mathrm{tot}</math>; the analytic expressions for these two ratios are presented in the last two rows of Table 1.
The expectation is that an increase in <math>\xi_i</math> along the sequence will correspond to an increase in the size — both the radius and the mass — of the core. This expectation is realized
|
Figure 1: Fractional mass versus fractional radius along the equilibrium sequence |
|
|
Analytic BiPolytrope with <math>n_c=5</math>, <math>n_e = 1</math>, and <math>\mu_e/\mu_c = 0.2</math> |
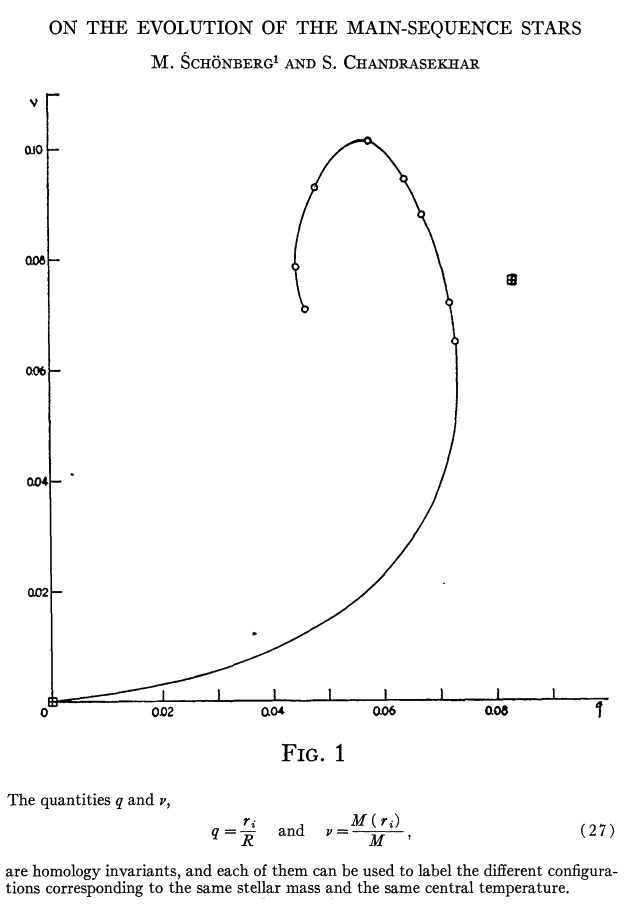
Edited excerpt from Schönberg & Chandrasekhar (1942) |
|
Plot of fractional core mass (<math>\nu</math>) versus fractional core radius (<math>q</math>) for the analytic bipolytrope having <math>\mu_e/\mu_c = 0.2</math>. The behavior of this analytically defined model sequence closely resembles the behavior of the numerically constructed isothermal core model presented by Schönberg & Chandrasekhar (1942). |
|
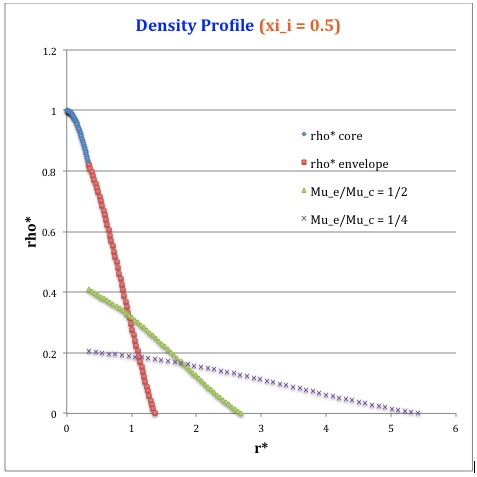
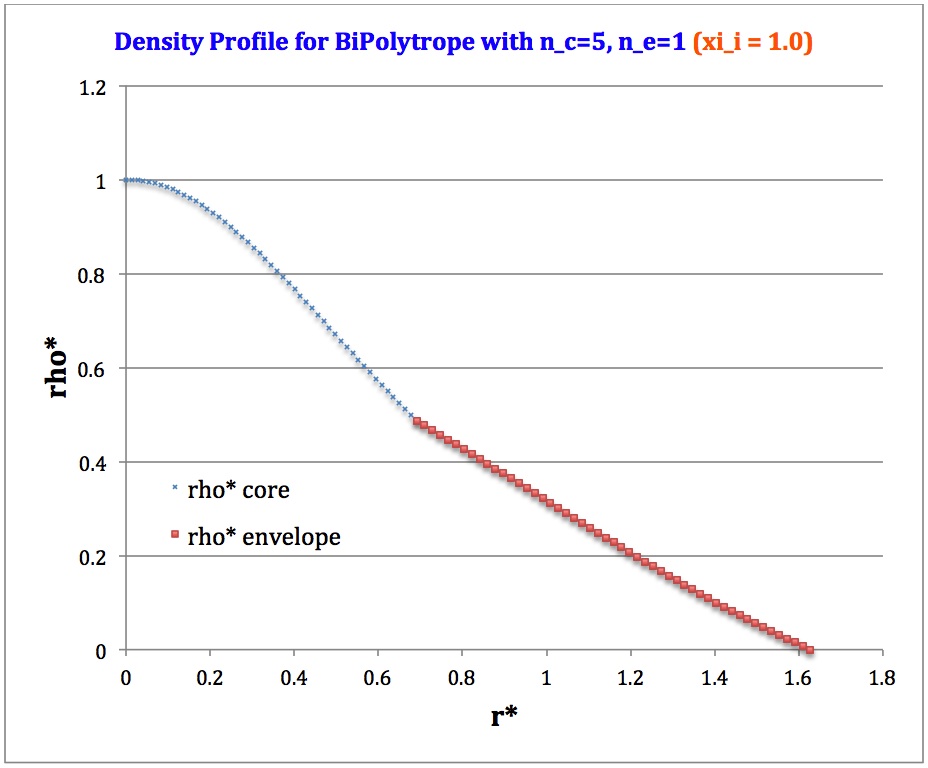
Profile
Table 2: Radial Profile of Various Physical Variables
|
Variable |
Throughout the Core |
Throughout the Envelope† |
Plotted Profiles |
||
|
<math>\xi_i = 0.5</math> |
<math>\xi_i = 1.0</math> |
<math>\xi_i = 3.0</math> |
|||
|
<math>r^*</math> |
<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta</math> |
|
||
|
<math>\rho^*</math> |
<math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2}</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i \phi(\eta)</math> |
|||
|
<math>P^*</math> |
<math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3}</math> |
<math>\theta^{6}_i [\phi(\eta)]^{2}</math> |
|||
|
<math>M_r^*</math> |
<math>\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
|
||
|
†In order to obtain the various envelope profiles, it is necessary to evaluate <math>\phi(\eta)</math> and its first derivative using the information presented in Step 6, above. |
|||||
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |