Difference between revisions of "User:Tohline/SSC/Structure/IsothermalSphere"
(Create page to discuss Emden's solution for the isothermal sphere) |
(→Governing Relations: Discuss Emden's derivation, including Table 14) |
||
| Line 63: | Line 63: | ||
<td align="center"> | <td align="center"> | ||
[[File:EmdenIsothermalDerivation.jpg|500px|center|Emden (1907)]] | [[File:EmdenIsothermalDerivation.jpg|500px|center|Emden (1907)]] | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
By adopting the following dimensionless variables, | |||
<div align="center"> | |||
<math> | |||
\mathfrak{r}_1 \equiv \rho_c^{1/2} \beta r \, , ~~~~\mathrm{and}~~~~v_1 \equiv \ln(\rho/\rho_c) \, , | |||
</math> | |||
</div> | |||
the governing ODE can be written in dimensionless form as, | |||
<div align="center"> | |||
<math> | |||
\frac{d^2v_1}{d\mathfrak{r}_1^2} +\frac{2}{\mathfrak{r}_1} \frac{dv_1}{dr} + e^{v_1} = 0 \, , | |||
</math> | |||
</div> | |||
which is exactly the equation that can be found on p. 133 of [http://books.google.com/books?id=MiDQAAAAMAAJ&printsec=frontcover#v=onepage&q&f=true Emden (1907)], numbered (II"a). | |||
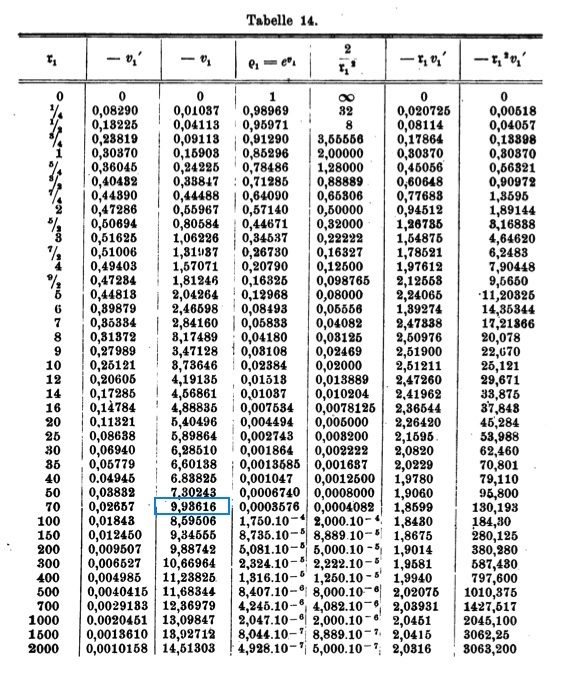
Emden numerically determined the behavior of the function <math>v_1(\mathfrak{r}_1)</math>, its first derivative with respect to <math>\mathfrak{r}_1</math>, <math>v_1'</math>, along with <math>e^{v_1}</math> and several other useful products, and published his results as Table 14, on p. 135 of his book. The table is reproduced here, mostly for historical purposes. | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="center"> | |||
[[File:EmdenTable14.jpg|600px|center|Emden's (1907) Table 14]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 01:44, 29 October 2012

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Isothermal Sphere (structure)
Here we supplement the simplified set of principal governing equations with an isothermal equation of state, that is, <math>~P</math> is related to <math>~\rho</math> through the relation,
<math>P = c_s^2 \rho \, ,</math>
where, <math>c_s</math> is the isothermal sound speed. Comparing this <math>~P</math>-<math>~\rho</math> relationship to
Form A
of the Ideal Gas Equation of State,
|
<math>~P_\mathrm{gas} = \frac{\Re}{\bar{\mu}} \rho T</math> |
we see that,
<math>c_s^2 = \frac{\Re T}{\bar{\mu}} = \frac{k T}{m_u \bar{\mu}} \, ,</math>
where, <math>~\Re</math>, <math>~k</math>, <math>~m_u</math>, and <math>~\bar{\mu}</math> are all defined in the accompanying variables appendix. It will be useful to note that, for an isothermal gas, <math>~H</math> is related to <math>~\rho</math> via the expression,
<math> dH = \frac{dP}{\rho} = c_s^2 d\ln\rho \, . </math>
Governing Relations
Adopting solution technique #2, we need to solve the following second-order ODE relating the two unknown functions, <math>~\rho</math> and <math>~H</math>:
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{dH}{dr} \biggr) =- 4\pi G \rho</math> .
Using the <math>~H</math>-<math>~\rho</math> relationship for an isothermal gas presented above, this can be rewritten entirely in terms of the density as,
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{d\ln\rho}{dr} \biggr) =- \frac{4\pi G}{c_s^2} \rho \, ,</math>
or, equivalently,
<math> \frac{d^2\ln\rho}{dr^2} +\frac{2}{r} \frac{d\ln\rho}{dr} + \beta^2 \rho = 0 \, , </math>
where,
<math> \beta^2 \equiv \frac{4\pi G}{c_s^2} \, . </math>
This matches the governing ODE whose derivation was published on p. 131 of Robert Emden's (1907) book titled, Gaskugeln.
|
Derivation by Emden (edited) |
|
By adopting the following dimensionless variables,
<math> \mathfrak{r}_1 \equiv \rho_c^{1/2} \beta r \, , ~~~~\mathrm{and}~~~~v_1 \equiv \ln(\rho/\rho_c) \, , </math>
the governing ODE can be written in dimensionless form as,
<math> \frac{d^2v_1}{d\mathfrak{r}_1^2} +\frac{2}{\mathfrak{r}_1} \frac{dv_1}{dr} + e^{v_1} = 0 \, , </math>
which is exactly the equation that can be found on p. 133 of Emden (1907), numbered (II"a). Emden numerically determined the behavior of the function <math>v_1(\mathfrak{r}_1)</math>, its first derivative with respect to <math>\mathfrak{r}_1</math>, <math>v_1'</math>, along with <math>e^{v_1}</math> and several other useful products, and published his results as Table 14, on p. 135 of his book. The table is reproduced here, mostly for historical purposes.
Bonnor and Ebert
In their studies of pressure-bounded isothermal spheres, Ebert (1955, ZA, 37, 217) and Bonnor (1956, MNRAS, 116, 351) both started with this governing ODE, but developed its solution in different ways. Here we present both developments while highlighting transformations between the two.
| Derivation by Bonnor (edited) | translation | Derivation by Ebert (edited) |
| <math>G \Leftrightarrow \gamma</math> | ||
| <math>\rho_c \Leftrightarrow \rho_0</math> | ||
| <math>\frac{kT}{m} \Leftarrow c_s^2 \Rightarrow \frac{\Re T_0}{\mu}</math> | ||
| <math>\beta^{1/2}\lambda^{-1/2} \Leftrightarrow l_0</math> | ||
| <math>e^{-\psi} \Leftrightarrow \eta</math> |
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |