Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt5"
(Created page with '__FORCETOC__<!-- will force the creation of a Table of Contents --> <!-- __NOTOC__ will force TOC off --> =Challenges Constructing Ellipsoidal-Like Configurations (Pt. 5)= This…') |
|||
| Line 7: | Line 7: | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
== | ==Tilted Plane Intersects Ellipsoid== | ||
In a [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#TippedPlane|an early subsection of the accompanying discussion]], we have pointed out that the intersection of each Lagrangian fluid element's tipped orbital plane with the surface of the (purple) ellipsoidal surface is given by the (unprimed) body-frame coordinates that simultaneously satisfy the expressions, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{x}{a}\biggr)^2 + \biggl( \frac{y}{b}\biggr)^2 + \biggl( \frac{z}{c}\biggr)^2 </math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~z</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~y \tan\theta + z_0 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where z<sub>0</sub> is the location where the tipped plane intersects the z-axis of the body frame. Combining these two expressions, we see that an intersection between the tipped plane and the ellipsoidal surface will occur at (x, y)-coordinate pairs that satisfy what we will henceforth refer to as the, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><font color="maroon">'''Intersection Expression'''</font></td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~1 - \frac{x^2}{a^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math> | |||
</td> | |||
</tr> | |||
</table> | |||
as long as z<sub>0</sub> lies within the range, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~z_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\le</math> | |||
</td> | |||
<td align="left"> | |||
<math>~c^2 + b^2\tan^2\theta \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
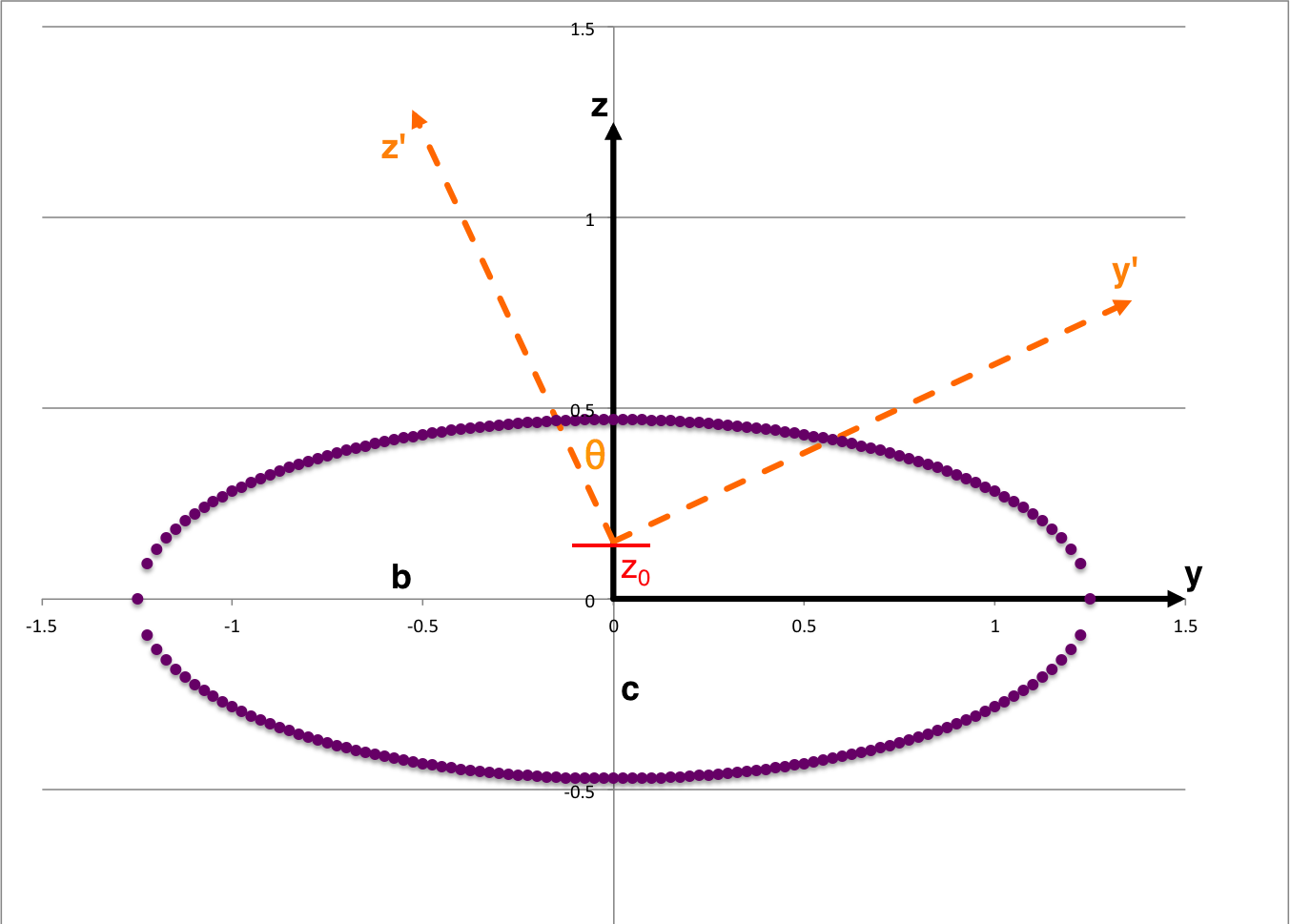
<span id="Fig1">Before calling upon any of Riemann's model parameters</span>, from geometric considerations alone we should be able to determine exactly what the expression is for any off-center ellipse that results from slicing — at a tipped angle — the chosen ellipsoid. | |||
<table border="1" width="50%" cellpadding="8" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><b>Figure 1</b></td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x' \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~y</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
y' \cos\theta - z'\sin\theta | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~(z - z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z' \cos\theta + y'\sin\theta | |||
\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center">[[File:ExcelAxes02C.png|400px|Primed Coordinates]]</td> | |||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~y'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
y \cos\theta + (z - z_0) \sin\theta | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~z'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(z-z_0) \cos\theta - y \sin\theta | |||
\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
In the equatorial plane of the ''tipped'' coordinate system — that is, after mapping <math>~x \rightarrow x'</math> and <math>~y \rightarrow (y' \cos\theta - z'\sin\theta)</math>, then setting <math>~z' = 0</math> — this intersection expression becomes, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a \biggl\{ 1 - \biggl[ (y'\cos\theta)^2 \biggl( \frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr) + y'\cos\theta | |||
\biggl( \frac{2z_0 \tan\theta}{c^2} \biggr) + \frac{z_0^2}{c^2} \biggr] \biggr\}^{1 / 2}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
=See Also= | =See Also= | ||
Revision as of 22:06, 11 May 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 5)
This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1), (Pt. 2), (Pt. 3), and (Pt. 4).

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Tilted Plane Intersects Ellipsoid
In a an early subsection of the accompanying discussion, we have pointed out that the intersection of each Lagrangian fluid element's tipped orbital plane with the surface of the (purple) ellipsoidal surface is given by the (unprimed) body-frame coordinates that simultaneously satisfy the expressions,
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl( \frac{x}{a}\biggr)^2 + \biggl( \frac{y}{b}\biggr)^2 + \biggl( \frac{z}{c}\biggr)^2 </math> |
and, |
<math>~z</math> |
<math>~=</math> |
<math>~y \tan\theta + z_0 \, ,</math> |
where z0 is the location where the tipped plane intersects the z-axis of the body frame. Combining these two expressions, we see that an intersection between the tipped plane and the ellipsoidal surface will occur at (x, y)-coordinate pairs that satisfy what we will henceforth refer to as the,
| Intersection Expression | ||
|
<math>~1 - \frac{x^2}{a^2} </math> |
<math>~=</math> |
<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math> |
as long as z0 lies within the range,
|
<math>~z_0^2</math> |
<math>~\le</math> |
<math>~c^2 + b^2\tan^2\theta \, .</math> |
Before calling upon any of Riemann's model parameters, from geometric considerations alone we should be able to determine exactly what the expression is for any off-center ellipse that results from slicing — at a tipped angle — the chosen ellipsoid.
In the equatorial plane of the tipped coordinate system — that is, after mapping <math>~x \rightarrow x'</math> and <math>~y \rightarrow (y' \cos\theta - z'\sin\theta)</math>, then setting <math>~z' = 0</math> — this intersection expression becomes,
|
<math>~x'</math> |
<math>~=</math> |
<math>~a \biggl\{ 1 - \biggl[ (y'\cos\theta)^2 \biggl( \frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr) + y'\cos\theta \biggl( \frac{2z_0 \tan\theta}{c^2} \biggr) + \frac{z_0^2}{c^2} \biggr] \biggr\}^{1 / 2}</math> |
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Construction Challenges (Pt. 4)
- Construction Challenges (Pt. 5)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |