Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2"
| Line 9: | Line 9: | ||
==Motivation== | ==Motivation== | ||
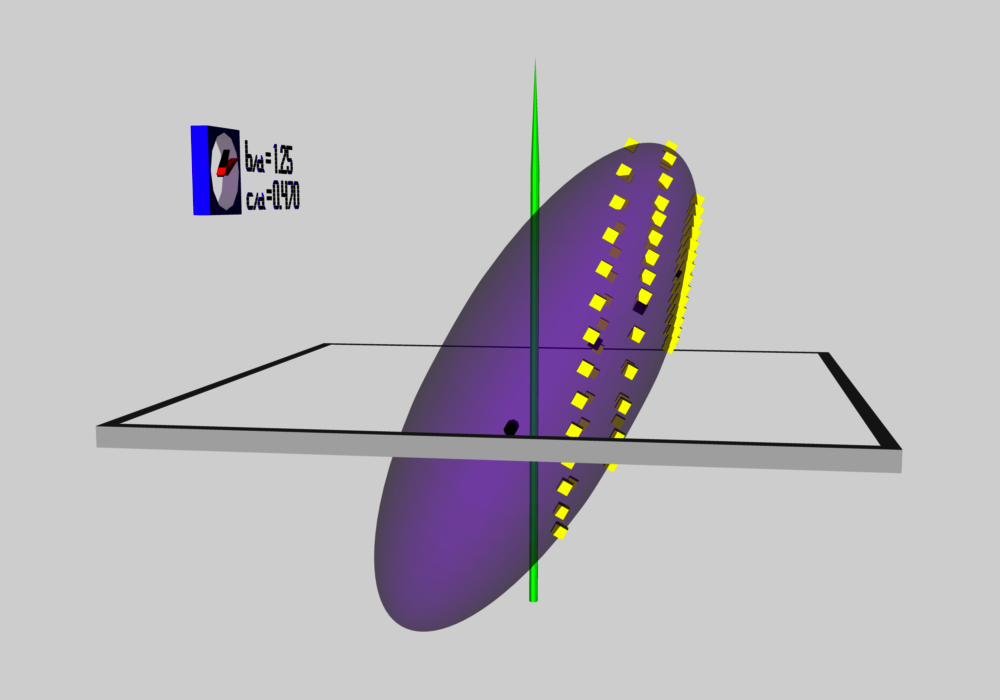
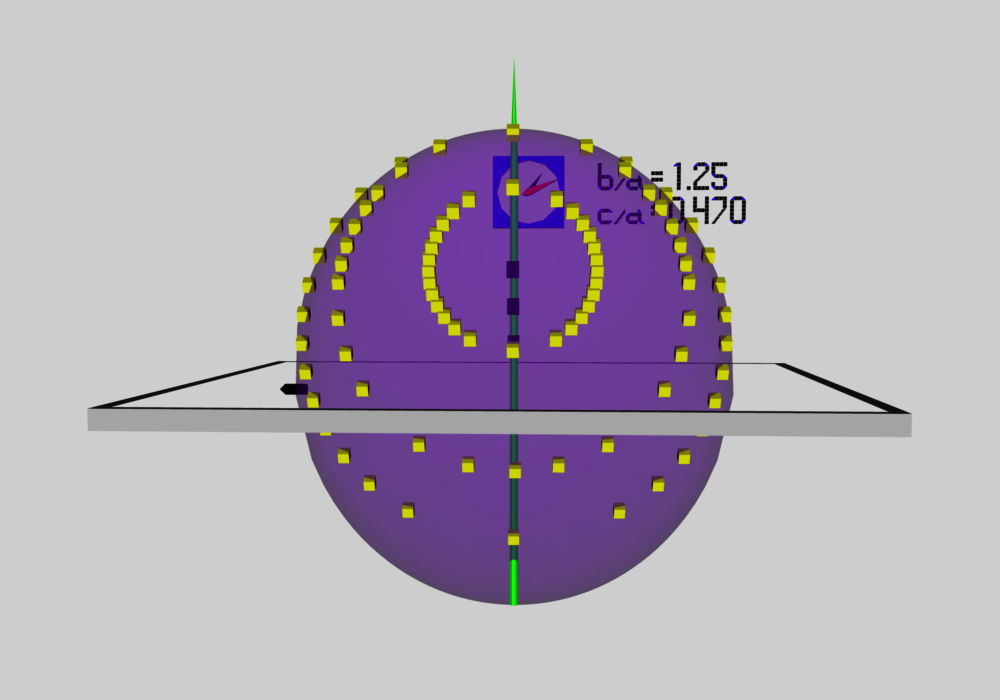
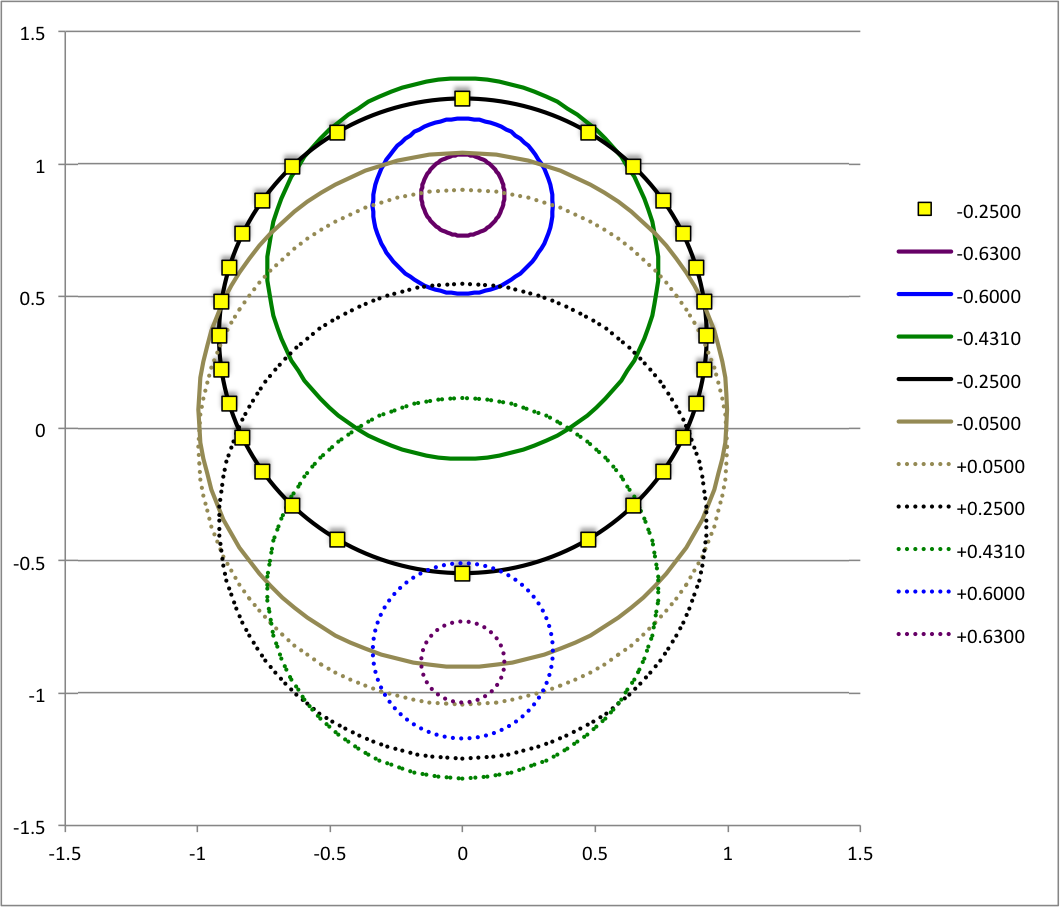
As has been described in an [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Figure3|accompanying discussion of Riemann Type 1 ellipsoids]], we have used COLLADA to construct an animated and interactive 3D scene that displays in purple the surface of an example Type I ellipsoid; panels a and b of Figure 1 show what this ellipsoid looks like when viewed from two different perspectives. (As a reminder — see the [[#explanation| explanation accompanying Figure 2 of that accompanying discussion]] — the ellipsoid is tilted about the x-coordinate axis at an angle of 61.25° to the equilibrium spin axis, which is shown in green.) Yellow markers also have been placed in this 3D scene at each of the coordinate locations specified in the [[#ExampleTrajectories|table that accompanies that discussion]]. From the perspective presented in Figure 3b, we can immediately identify three separate, nearly circular trajectories; the largest one corresponds to our choice of z<sub>0</sub> = -0.25, the smallest corresponds to our choice of z<sub>0</sub> = -0.60, and the one of intermediate size correspond to our choice of z<sub>0</sub> = -0.4310. When viewed from the perspective presented in Figure 1a, we see that these three trajectories define three separate planes; each plane is tipped at an angle of θ = -19.02° to the ''untilted'' equatorial, x-y plane of the purple ellipsoid. | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center">Figure 1a</th> | |||
<th align="center">Figure 1b</th> | |||
</tr> | |||
<tr> | |||
<td align="left" bgcolor="lightgrey"> | |||
[[File:B125c470B.cropped.png|400px|EFE Model b41c385]] | |||
</td> | |||
<td align="left" bgcolor="lightgrey"> | |||
[[File:B125c470A.cropped.png|400px|EFE Model b41c385]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<th align="center" colspan="2">Figure 1c</th> | |||
</tr> | |||
<tr> | |||
<td align="center" bgcolor="white" colspan="2"> | |||
[[File:ProjectedOrbitsFlipped2.png|600px|EFE Model b41c385]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=See Also= | =See Also= | ||
Revision as of 21:59, 5 April 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 2)
This chapter extends an accompanying chapter titled, Construction Challenges (Pt. 1). The focus here is on an SCF technique that will incorporate specification of a Lagrangian flow-flied.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Motivation
As has been described in an accompanying discussion of Riemann Type 1 ellipsoids, we have used COLLADA to construct an animated and interactive 3D scene that displays in purple the surface of an example Type I ellipsoid; panels a and b of Figure 1 show what this ellipsoid looks like when viewed from two different perspectives. (As a reminder — see the explanation accompanying Figure 2 of that accompanying discussion — the ellipsoid is tilted about the x-coordinate axis at an angle of 61.25° to the equilibrium spin axis, which is shown in green.) Yellow markers also have been placed in this 3D scene at each of the coordinate locations specified in the table that accompanies that discussion. From the perspective presented in Figure 3b, we can immediately identify three separate, nearly circular trajectories; the largest one corresponds to our choice of z0 = -0.25, the smallest corresponds to our choice of z0 = -0.60, and the one of intermediate size correspond to our choice of z0 = -0.4310. When viewed from the perspective presented in Figure 1a, we see that these three trajectories define three separate planes; each plane is tipped at an angle of θ = -19.02° to the untilted equatorial, x-y plane of the purple ellipsoid.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |