Difference between revisions of "User:Tohline/Appendix/Ramblings/ForOuShangli"
| Line 4: | Line 4: | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
In order to download any one of the COLLADA-based files referenced below, go to [http://phys.lsu.edu/tohline/COLLADA http://phys.lsu.edu/tohline/COLLADA]. | |||
==EFE Diagram (Review)== | ==EFE Diagram (Review)== | ||
| Line 314: | Line 316: | ||
</tr> | </tr> | ||
</table> | </table> | ||
=See Also= | =See Also= | ||
Revision as of 19:40, 27 January 2021
For Shangli Ou

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
In order to download any one of the COLLADA-based files referenced below, go to http://phys.lsu.edu/tohline/COLLADA.
EFE Diagram (Review)
| Figure 1 |
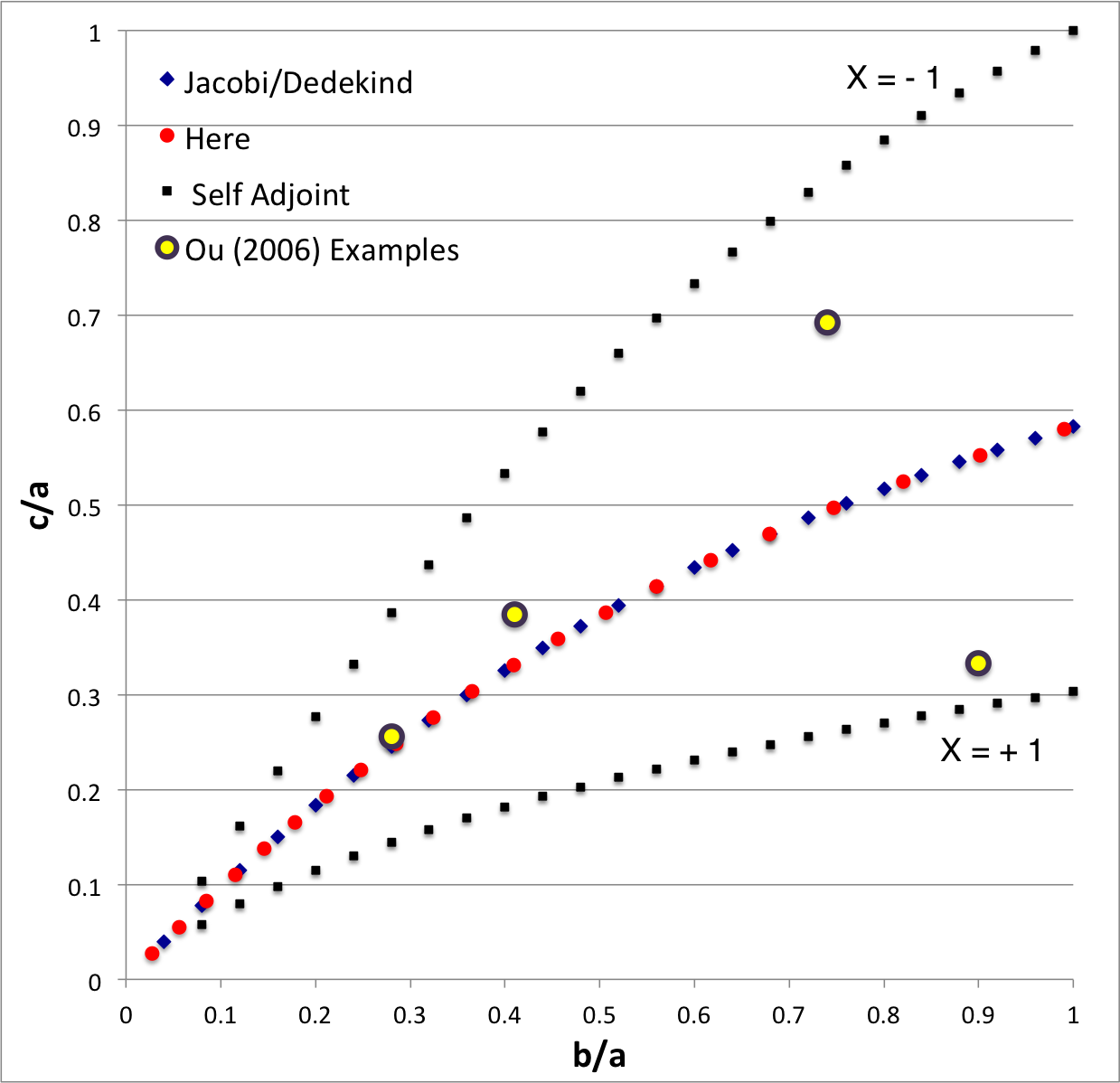
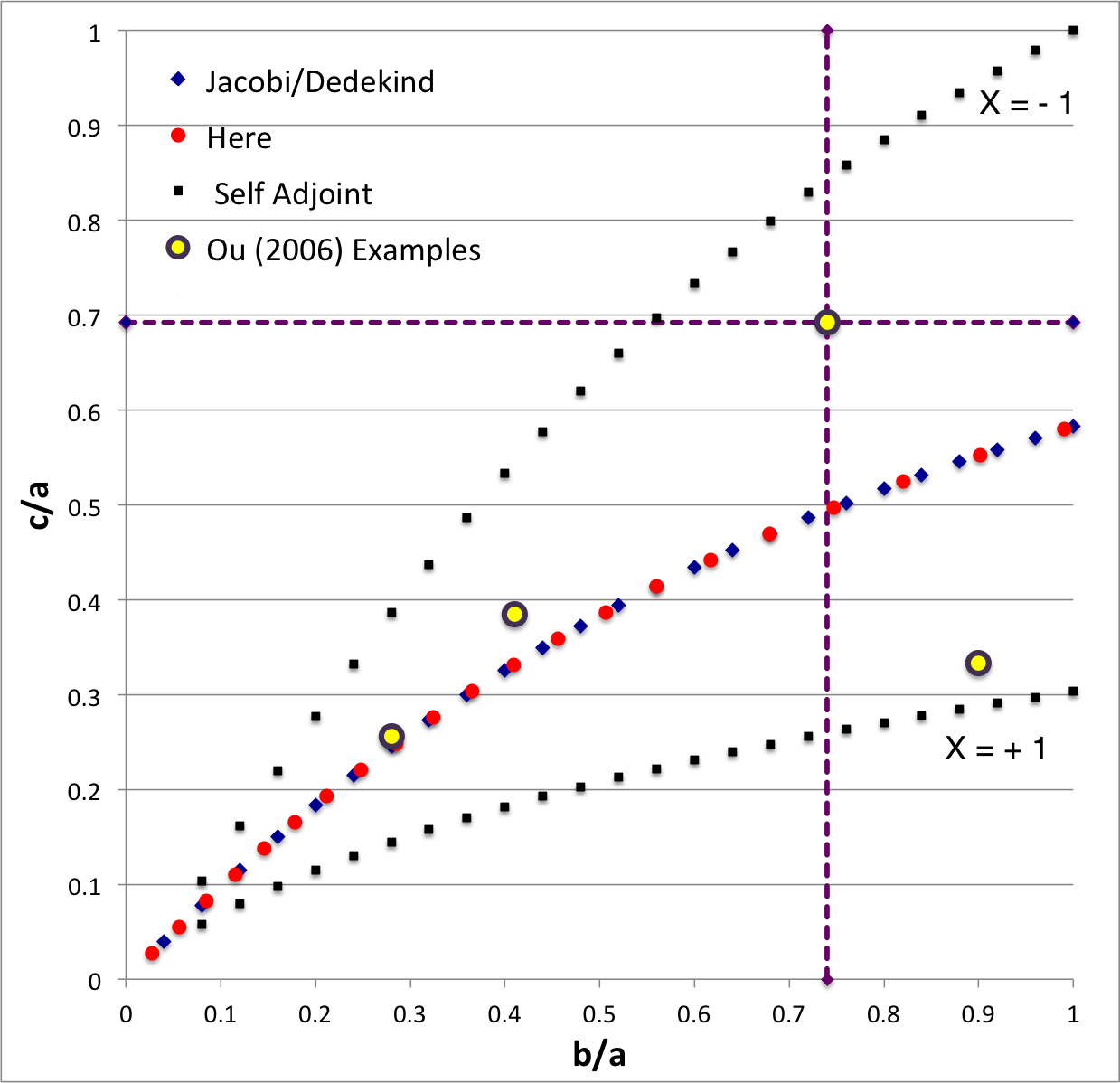
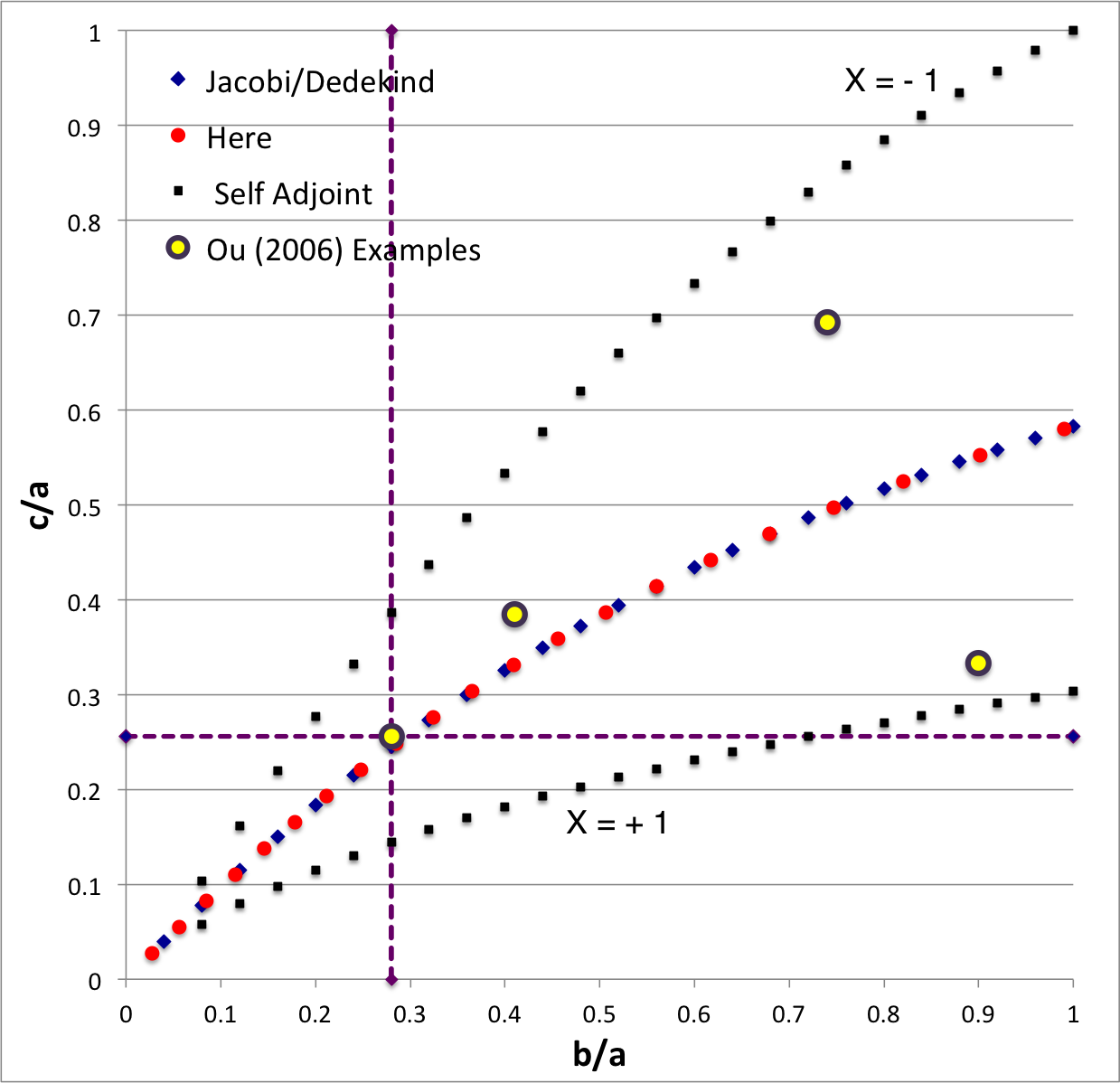
In the context of our broad discussion of ellipsoidal figures of equilibrium, the label "EFE Diagram" refers to a two-dimensional parameter space defined by the pair of axis ratios (b/a, c/a), usually covering the ranges, 0 ≤ b/a ≤ 1 and 0 ≤ c/a ≤ 1. The classic/original version of this diagram appears as Figure 2 on p. 902 of S. Chandrasekhar (1965, ApJ, vol. 142, pp. 890-921); a somewhat less cluttered version appears on p. 147 of Chandrasekhar's [EFE].
The version of the EFE Diagram shown here, on the left, highlights four model sequences, all of which also can be found in the original version:
- Jacobi sequence — the smooth curve that runs through the set of small, dark-blue, diamond-shaped markers; the data identifying the location of these markers have been drawn from §39, Table IV of [EFE]. The small red circular markers lie along this same sequence; their locations are taken from our own determinations, as detailed in Table 2 of our accompanying discussion of Jacobi ellipsoids. All of the models along this sequence have <math>~f \equiv \zeta/\Omega_f = 0</math> and are therefore solid-body rotators, that is, there is no internal motion when the configuration is viewed from a frame that is rotating with frequency, <math>~\Omega_f</math>.
- Dedekind sequence — a smooth curve that lies precisely on top of the Jacobi sequence. Each configuration along this sequence is adjoint to a model on the Jacobi sequence that shares its (b/a, c/a) axis-ratio pair. All ellipsoidal figures along this sequence have <math>~1/f = \Omega_f/\zeta = 0</math> and are therefore stationary as viewed from the inertial frame; the angular momentum of each configuration is stored in its internal motion (vorticity).
- The X = -1 self-adjoint sequence — At every point along this sequence, the value of the key frequency ratio, <math>~\zeta/\Omega_f</math>, in the adjoint configuration <math>~(f_+)</math> is identical to the value of the frequency ratio in the direct configuration <math>~(f_-)</math>; specifically, <math>~f_+ = f_- = -(a^2+b^2)/(ab)</math>. The data identifying the location of the small, solid-black markers along this sequence have been drawn from §48, Table VI of [EFE].
- The X = +1 self-adjoint sequence — At every point along this sequence, the value of the key frequency ratio, <math>~\zeta/\Omega_f</math>, in the adjoint configuration <math>~(f_+)</math> is identical to the value of the frequency ratio in the direct configuration <math>~(f_-)</math>; specifically, <math>~f_+ = f_- = +(a^2+b^2)/(ab)</math>. The data identifying the location of the small, solid-black markers along this sequence have been drawn from §48, Table VI of [EFE].
Riemann S-type ellipsoids all lie between or on the two (self-adjoint) curves marked "X = -1" and "X = +1" in the EFE Diagram. The yellow circular markers in the diagram shown here, on the left, identify four Riemann S-type ellipsoids that were examined by Ou (2006) and that we have also chosen to use as examples.
Example 3D Interactive Animations
For details, see the accompanying chapter titled, "Riemann Meets COLLADA & Oculus Rift S".
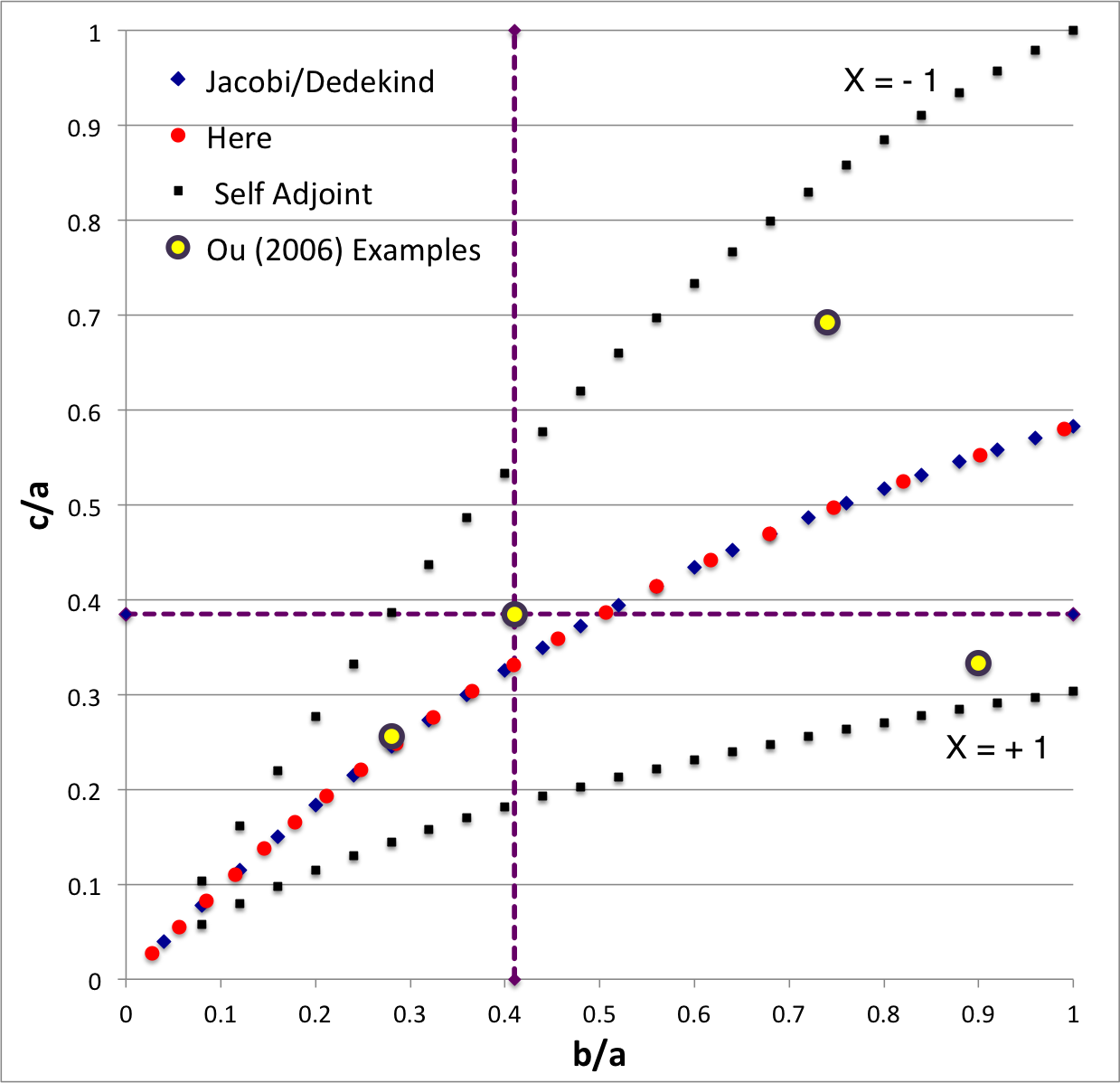
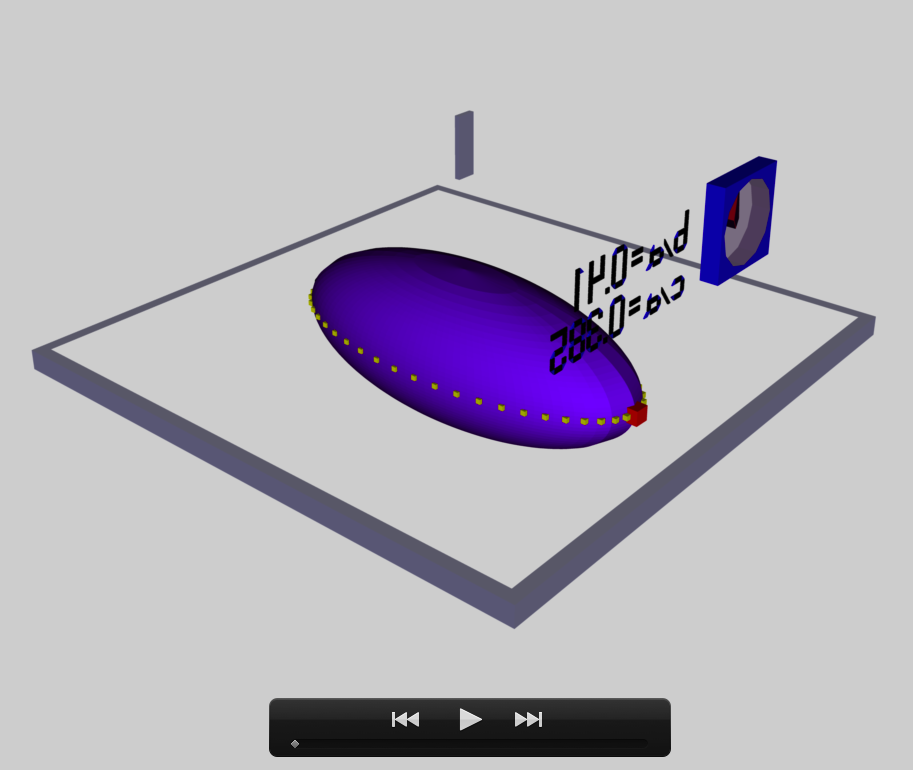
b41c385
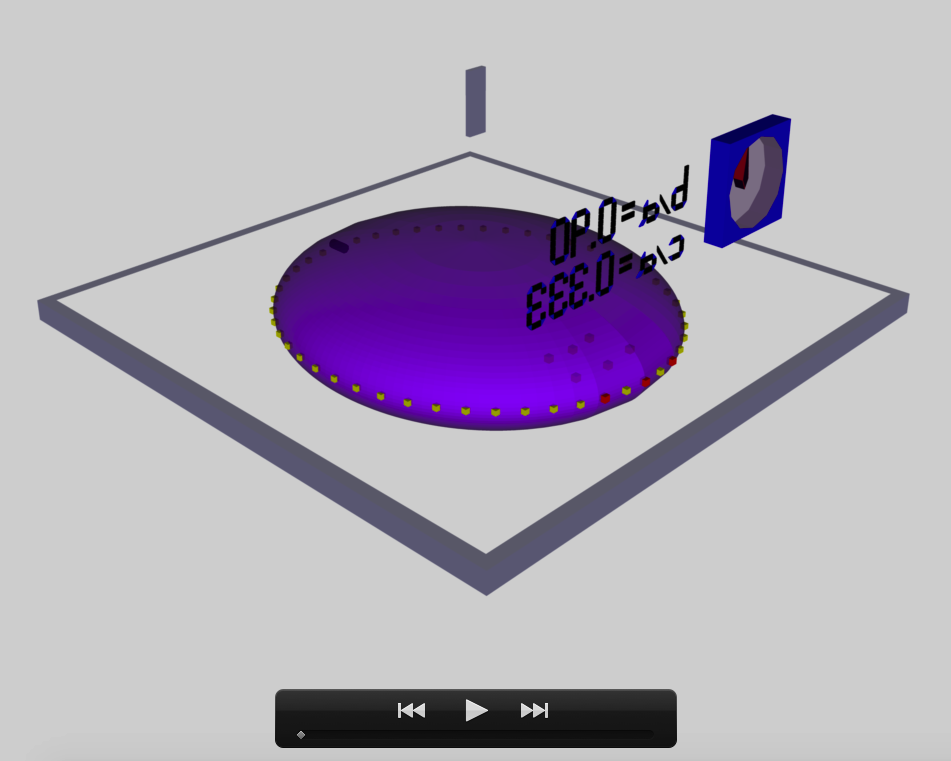
The model that we have chosen to use in our first successful construction of a COLLADA-based, 3D and interactive animation has the following properties; this model has been selected from Table 2 of our accompanying discussion of Riemann S-type ellipsoids:
|
|
<math>~\frac{b}{a} = 0.41</math> |
|
||||
|
<math>~\frac{c}{a} = 0.385</math> |
||||||
|
Direct |
|
Adjoint |
||||
|
<math>~\Omega_\mathrm{EFE} = 0.547874</math> |
<math>~\Omega_\mathrm{EFE} = - 0.079886</math> |
|||||
|
<math>~\lambda_\mathrm{EFE} = 0.079886</math> |
<math>~\lambda_\mathrm{EFE} = - 0.547874</math> |
|||||
|
<math>~f = - 0.415418</math> |
<math>~f = - 19.53923</math> |
|||||
The subscript "EFE" on Ω and λ means that the relevant frequency is given in units that have been adopted in [EFE], that is, in units of <math>~[\pi G\rho]^{1 / 2}</math>. In Figure 2a, the yellow circular marker, that has been placed where the pair of purple dashed lines cross, identifies the location of this model in the "c/a versus b/a" EFE Diagram that appears as Figure 2 on p. 902 of S. Chandrasekhar (1965); essentially the same diagram appears in §49 (p. 147) of [EFE].
In a separate chapter we have discussed various properties of uniformly rotating, Jacobi ellipsoids; they are equilibrium configurations that lie along the sequence that runs from "M2" (on the b/a = 1, Maclaurin sequence) to the origin of this diagram. Our chosen model lies off of — just above — the Jacobi-ellipsoid sequence, which means that it is not rotating as a solid body. Instead, as we focus first on the direct (as opposed to the adjoint) configuration, we appreciate that while the ellipsoid is spinning prograde (counter-clockwise) with a frequency given by |ΩEFE|, each Lagrangian fluid element inside as well as on the surface of the ellipsoid is traveling retrograde (clockwise) along an elliptical path with a frequency given by |λEFE|.
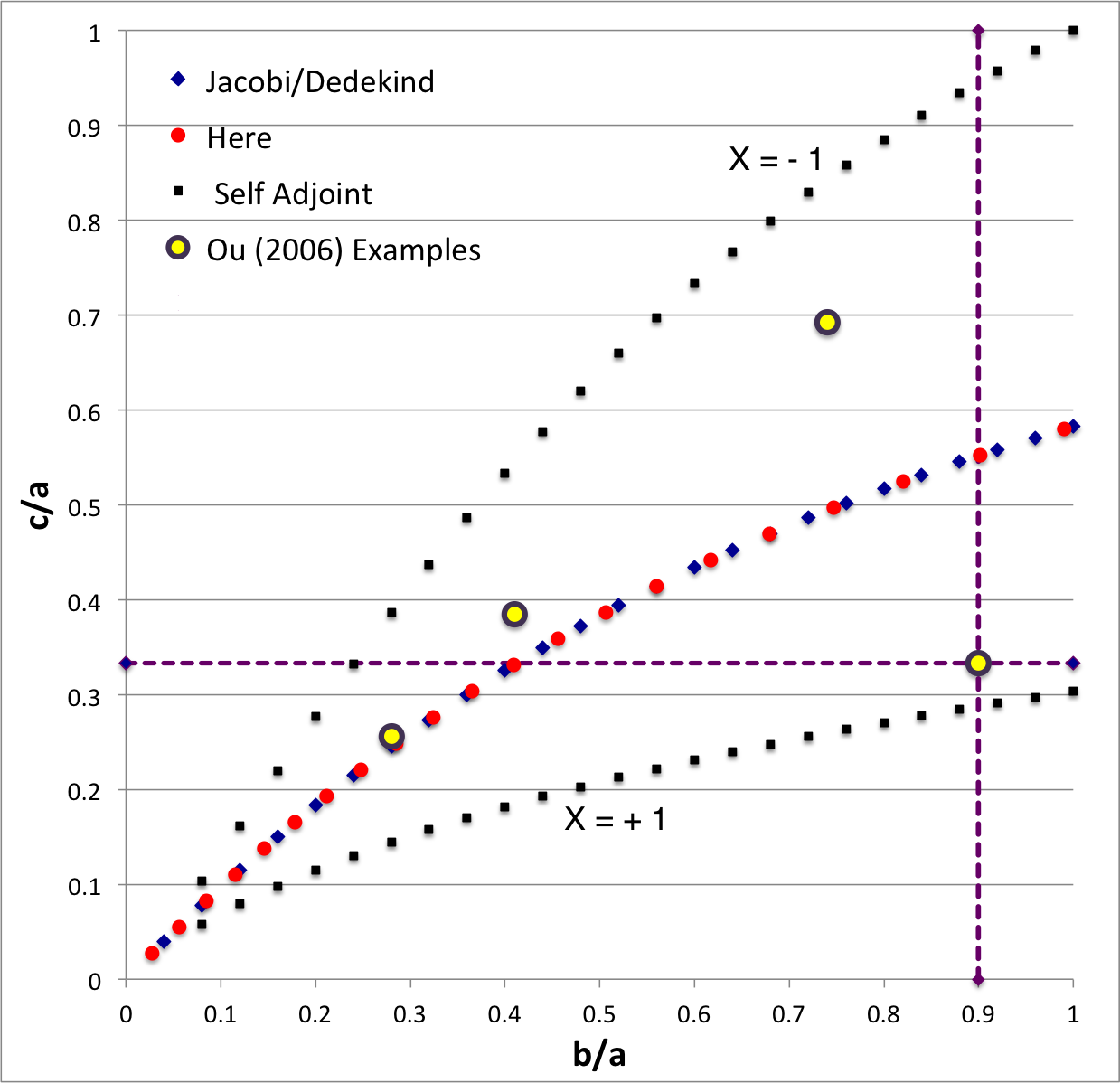
b90c333
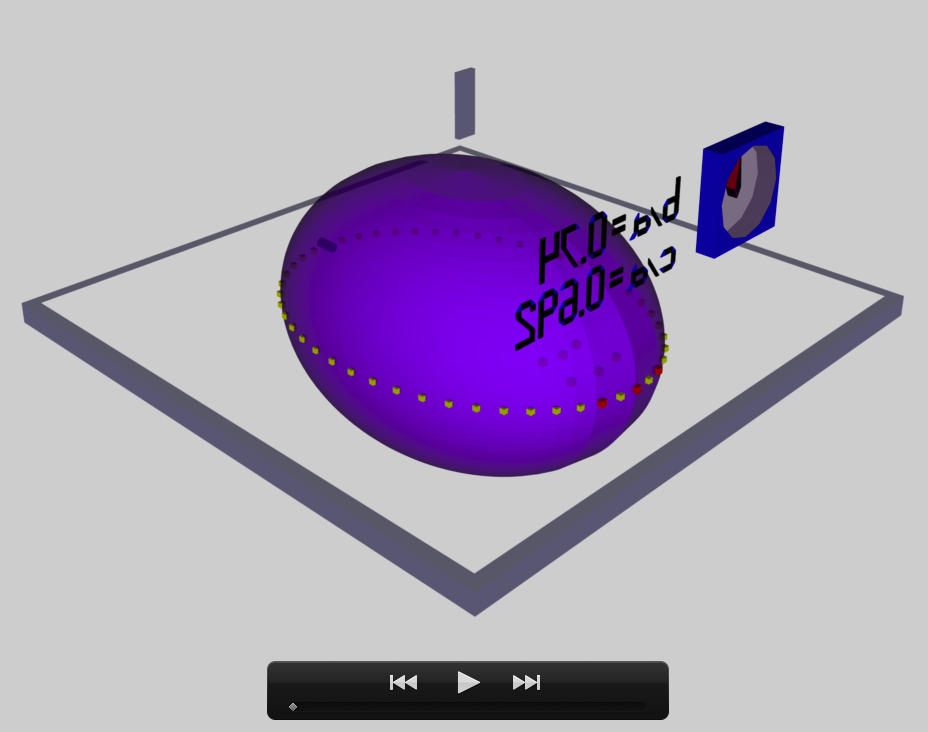
The model that we have chosen to use in our second successful construction of a COLLADA-based, 3D and interactive animation has the following properties; this model has been selected from Table 2 of our accompanying discussion of Riemann S-type ellipsoids:
|
|
<math>~\frac{b}{a} = 0.90</math> |
|
||||
|
<math>~\frac{c}{a} = 0.333</math> |
||||||
|
Direct |
|
Adjoint |
||||
|
<math>~\Omega_\mathrm{EFE} = 0.447158</math> |
<math>~\Omega_\mathrm{EFE} = 0.221411</math> |
|||||
|
<math>~\lambda_\mathrm{EFE} = - 0.221411</math> |
<math>~\lambda_\mathrm{EFE} = - 0.447158 </math> |
|||||
|
<math>~f = + 0.995805</math> |
<math>~f = + 4.061607 </math> |
|||||
b74c692
The model that we have chosen to use in our third successful construction of a COLLADA-based, 3D and interactive animation has the following properties; this model has been selected from Table 2 of our accompanying discussion of Riemann S-type ellipsoids:
|
|
<math>~\frac{b}{a} = 0.74</math> |
|
||||
|
<math>~\frac{c}{a} = 0.692</math> |
||||||
|
Direct |
|
Adjoint |
||||
|
<math>~\Omega_\mathrm{EFE} = 0.638747</math> |
<math>~\Omega_\mathrm{EFE} = - 0.217773</math> |
|||||
|
<math>~\lambda_\mathrm{EFE} = 0.217773</math> |
<math>~\lambda_\mathrm{EFE} = - 0.638747 </math> |
|||||
|
<math>~f = - 0.713019</math> |
<math>~f = - 6.13413 </math> |
|||||
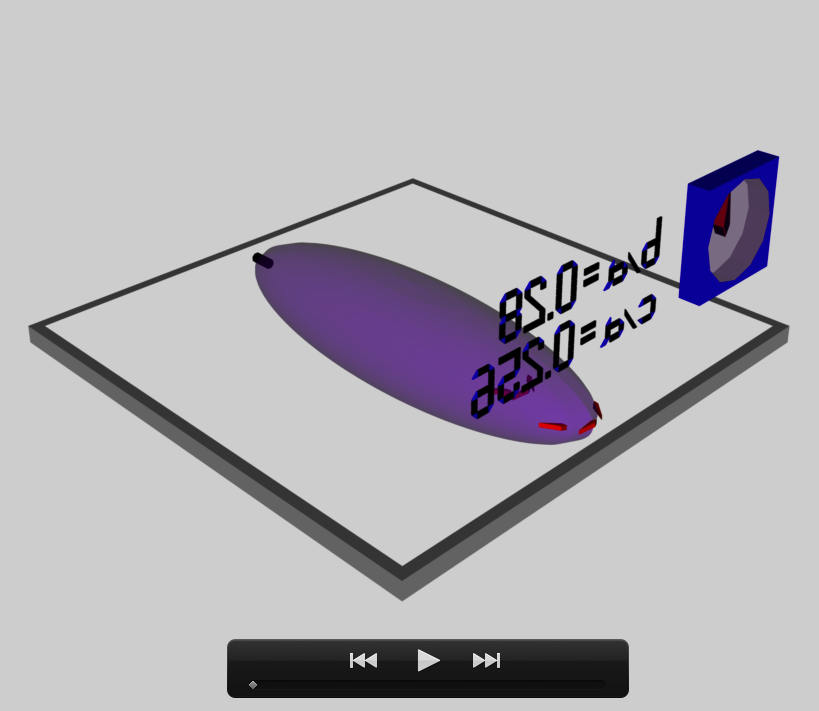
b28c256
The model that we have chosen to use in our second successful construction of a COLLADA-based, 3D and interactive animation has the following properties; this model has been selected from Table 2 of our accompanying discussion of Riemann S-type ellipsoids:
|
|
<math>~\frac{b}{a} = 0.28</math> |
|
||||
|
<math>~\frac{c}{a} = 0.256</math> |
||||||
|
Direct |
|
Adjoint |
||||
|
<math>~\Omega_\mathrm{EFE} = 0.456676</math> |
<math>~\Omega_\mathrm{EFE} = - 0.020692</math> |
|||||
|
<math>~\lambda_\mathrm{EFE} = 0.020692</math> |
<math>~\lambda_\mathrm{EFE} = - 0.456676</math> |
|||||
|
<math>~f = - 0.174510</math> |
<math>~f = - 85.0007</math> |
|||||
See Also
- Discussion of Ou's Riemann-Like Ellipsoids
- Riemann Meets COLLADA & Oculus Rift S: Example (b/a, c/a) = (0.41, 0.385)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |